明导向知算理 提升关键能力--例析二轮复习中数学核心素养的发展

江苏省海安高级中学 (226600) 徐卫华

高中数学的六大学科核心素养是高中数学课程体系与目标的一个集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,也是每年高考命题的一个主要方向．在二轮数学复习备考中,教师应该基于课堂,深耕课堂,合理构建学科教学观念与现代教学模式,突破传统教学方式的束缚与单一数学知识的局限,全面优化数学教学策略,促进学生的全面发展．本文通过实例探析数学核心素养的发展.

例1 (开放题)已知函数f(x)满足:①f(0)=0;②在[1,3]上是减函数;③f(1+x)=f(1-x)．请写出一个满足以上条件的f(x)=________．

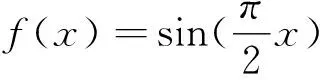
评注:解决一些涉及概念、性质等类型的开放结论“举例问题”时,关键是抓住题目条件中涉及概念、性质等相关信息加以数学抽象,借助一些熟知的数学基础知识入手进行对比分析,进而巧妙配凑出相应的符号、系数、运算关系等,实现多题目信息条件的交汇与整合,实现问题的破解．

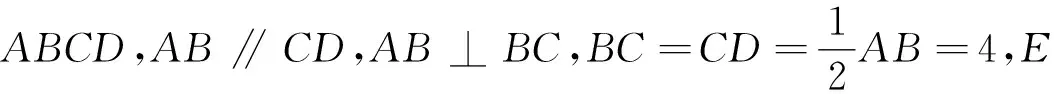
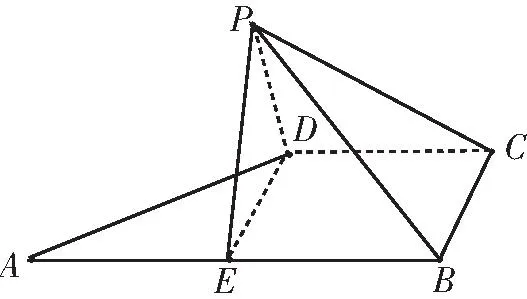
图1

A．EB⊥平面PED

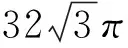
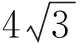
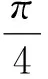
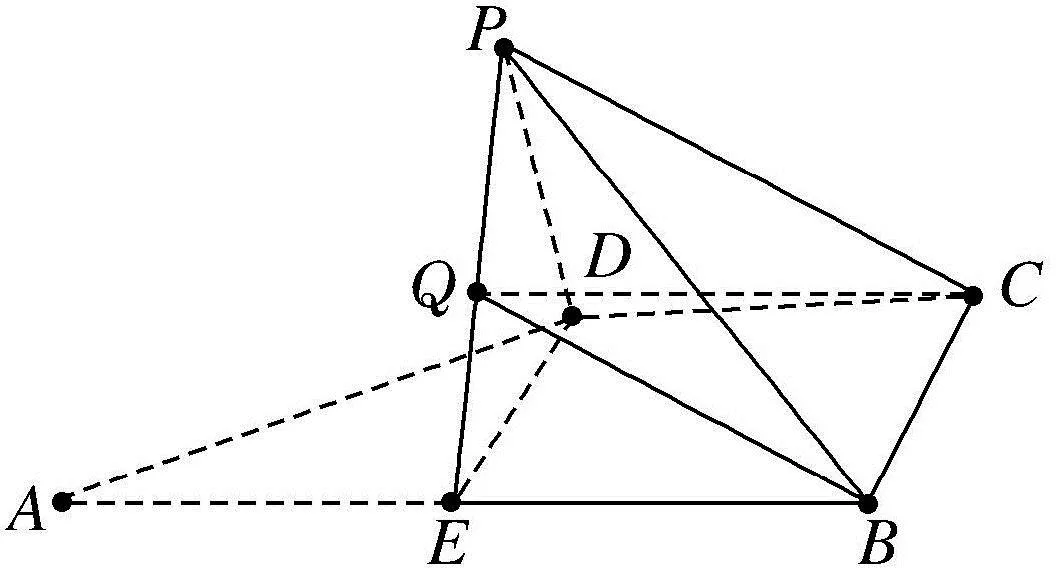
图2

评注:解决此类由平面几何图形折叠成空间几何体问题时,要充分利用直观想象,结合平面几何图形的直观与空间想象,观察折叠前后平面图形、立体图形与数量关系形态的变化与运动规律,进而为逻辑推理、数学运算解决问题提供基础．

例3 为了更好地管理班级,班主任决定选若干名学生担任班主任助理,于是征求语、数、英三科任课教师的意见．语文老师:如果不选小李,那么不选小宋;数学老师:如果不选小宋,那么选小李;英语老师:小宋和小李两人中至少选一个并且至多选一个．若班主任同时采纳了三人的建议,则作出的选择是( ).

A．选小宋,不选小李 B．选小李,不选小宋

C．两人都选 D．两人都不选

析解:根据题目条件,抓住题目叙述分别针对三位老师的意见进行逻辑推理与分析,进而为班主任对小李与小宋两位同学作出的选择提供依据．由英语老师的话易知,两人中选且只选一人,选项C、D错误;由语文老师的话易知,如果不选小李,那么不选小宋,选项A错误;由数学老师的话易知,如果不选小宋,那么选小李,选项B正确.故选B．

评注:涉及此类语言叙述的简单合情推理问题,关键是抓住各信息点的内涵与实质,通过不同信息点之间的共同点、矛盾点等加以比对、分析,合理借助准确、严谨的逻辑推理,剖析并解决推理论证问题．

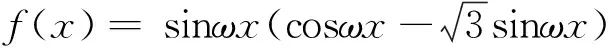
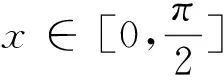
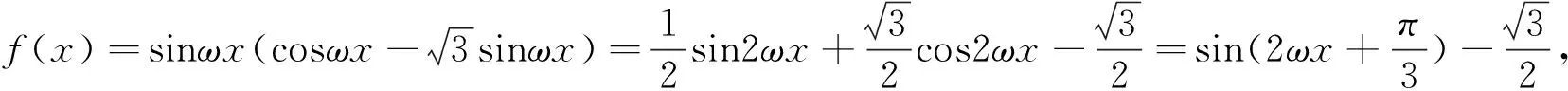
评注:解决一些涉及函数与方程、三角函数等相关问题是地,往往离不开最基本的数学运算,以及对相关公式的变形与转化．特别在解决一些三角函数问题中,三角恒等变换公式的应用以及合理确定运算技巧,选择配套的运算方法,是快速有效解决此类数学运算问题的关键所在．

例5 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图3所示,已知筒车的半径为4m,筒车转轮的中心O到水面的距离为2m,筒车沿逆时针方向以角速度ω(ω>0)转动,规定:盛水筒M对应的点P从水中浮现(即P0时的位置)时开始计算时间,且以水轮的圆心O为坐标原点,过点O的水平直线为x轴建立平面直角坐标系xOy,设盛水筒M从点P0运动到点P时经过的时间为t(单位:s),且此时点P距离水面的高度为h(单位:米),筒车经过6s第一次到达最高点,则下列叙述正确的是( ).

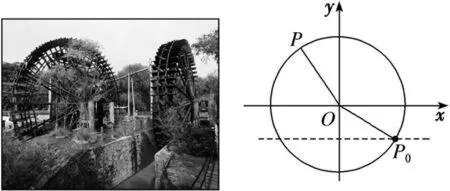
图3

A．当t=16s时,点P与点P0重合

B．当t∈[51,65]时,h一直在增大

C．当t∈(0,50)时,盛水筒有5次经过水平面

D．当t=50时,点P在最低点

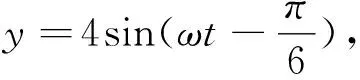
评注:数学建模是数学应用的一种重要形式,也是解决数学应用问题的最主要的模式,其能合理搭建了数学与外部世界的应用之间联系的桥梁,通过数学抽象与概括,综合数学知识、语言、表达方式等进一步加以应用,利用数学知识与方法构建相应的数学模型,进而加以“解模”与应用．

由以上实例可见,二轮复习备考中,教师要采用提升关键能力的手段,实现核心素养的提升目标,从各核心素养的视角,努力达到培养学生的“三会”能力.