新建隧道爆破振动对既有邻近设施的影响规律
2024-01-09操鹏
操 鹏
(中铁四院集团工程建设有限责任公司, 武汉 430063)
铁路运输作为社会生产、分配、交换、消费的联系纽带,对于国民经济的发展举足轻重。在邻近既有线爆破施工过程中,铁路的结构和运营安全是不容忽视的问题,而如何将爆破施工的影响范围控制在设计及理想安全状况的要求内则需要进一步研究新建隧道爆破振动对既有邻近设施的影响规律。
关于隧道爆破施工对邻近设施的影响,国内外已有较多的研究。已有文献主要采用现场监测和数值模拟两种手段来分析隧道的安全性。刘闵龙等[1]建立岩体各向异性动态损伤本构模型,通过数值模拟和现场损伤测试,验证该本构模型可用于爆破损伤模拟。徐振洋等[2]利用希尔伯特黄变换(Hilbert-Huang transform,HHT)对公路隧道爆破时邻近铁路隧道监测得到的振动信号进行分析,从能量的角度分析隧道受振动情况。张学民等[3]进行了近距离双线隧道的现场监测,针对层状围岩下的爆破参数进行了相应的优化。彭道富等[4-5]研究了相邻隧道爆破和隧道上部爆破两种情况对隧道结构以及爆破性质、地质条件对既有隧道结构振动的影响。张杰[6]、肖文芳等[7]运用理论分析和现场监测的方法选择了合适的施工方案和爆破设计方法,研究了地表爆破地震波的振动规律。熊祖钊等[8]从开挖方法、开挖顺序、爆破参数等方面给出适合的爆破开挖技术,为工程实践提供理论支持。李秀地等[9]利用DYNA内嵌炸药材料及状态方程模拟爆破过程,模拟新建隧道对近距离隧道结构的影响。
基于某隧道爆破掘进工程,为保证邻近既有线高速铁路在爆破施工过程中的运维安全,对其邻近隧道段进行爆破振动安全监测,获取爆破振动数据200余组。以测得的振动数据分析为基础,结合ANSYS LS-dyna有限元软件建立隧道爆破开挖对既有隧道影响分析的数值计算模型,通过仿真计算结果分析,得到隧道爆破开挖对邻近既有隧道内、路基、桥墩的爆破振动传播衰减规律,以期为工程实践提供可靠的理论依据。
1 工程实例
1.1 工程概况
新建某隧道为单洞双线隧道,设计时速为160 km/h,隧道进口轨道标高为114.41 m,出口轨道标高为133.71 m,距离某既有铁路最近点轨道高程差为12 m。该隧道所处地质中明洞27.01 m,占全隧道1.73%。Ⅲ级围岩510 m,占全隧32.71%,Ⅳ级围岩595 m,占全隧道38.17%,Ⅴ级围岩422 m,占全隧道27.07%。最大埋深98 m。
1.2 隧道掘进方案
隧道Ⅲ级围岩段采用台阶法爆破掘进,爆破循环进尺取为2.4 m,爆破规模为152 kg,最大单段药量为19.5 kg;Ⅳ级围岩段采用三台阶法爆破掘进,爆破循环进尺取为2 m,爆破规模为76.2 kg,最大单段药量为15 kg;Ⅴ级围岩段,采用三台阶七步开挖法爆破掘进,爆破循环进尺取为0.8 m,爆破规模为14.2 kg,最大单段药量为3.6 kg。明挖段台阶爆破,爆破规模为27.6 kg,最大单段药量为7.2 kg。
1.3 振动监测及分析
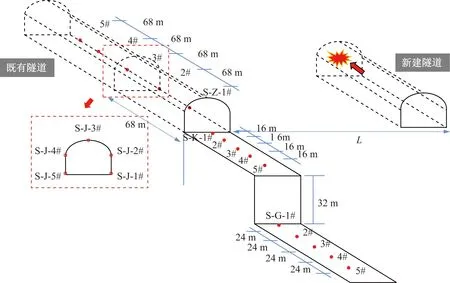
爆破施工区域为新建隧道,振动监测点布置在既有高速铁路迎爆侧路基路肩(或桥梁墩身顶部、隧道洞壁上、坚固基础),其中隧道测点距电缆槽盖板高度约1 m位置处。
本项目隧道爆破振动速度控制天窗点内报警值为3 cm/s,爆破预警值为2.55 cm/s;天窗点外施工报警值为1 cm/s,预警值为0.85 cm/s,控制值为0.5 cm/s,预警值为0.4 cm/s。监测点布置如图1所示。
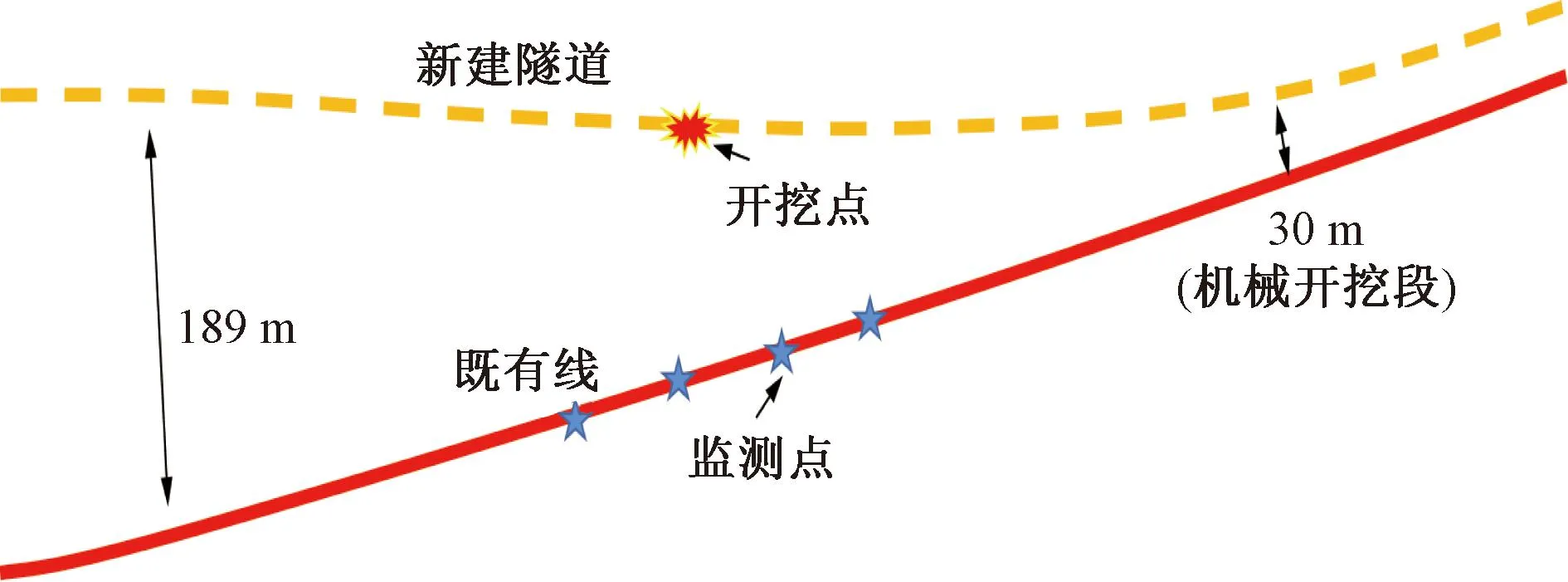
图1 爆破振动监测点布置
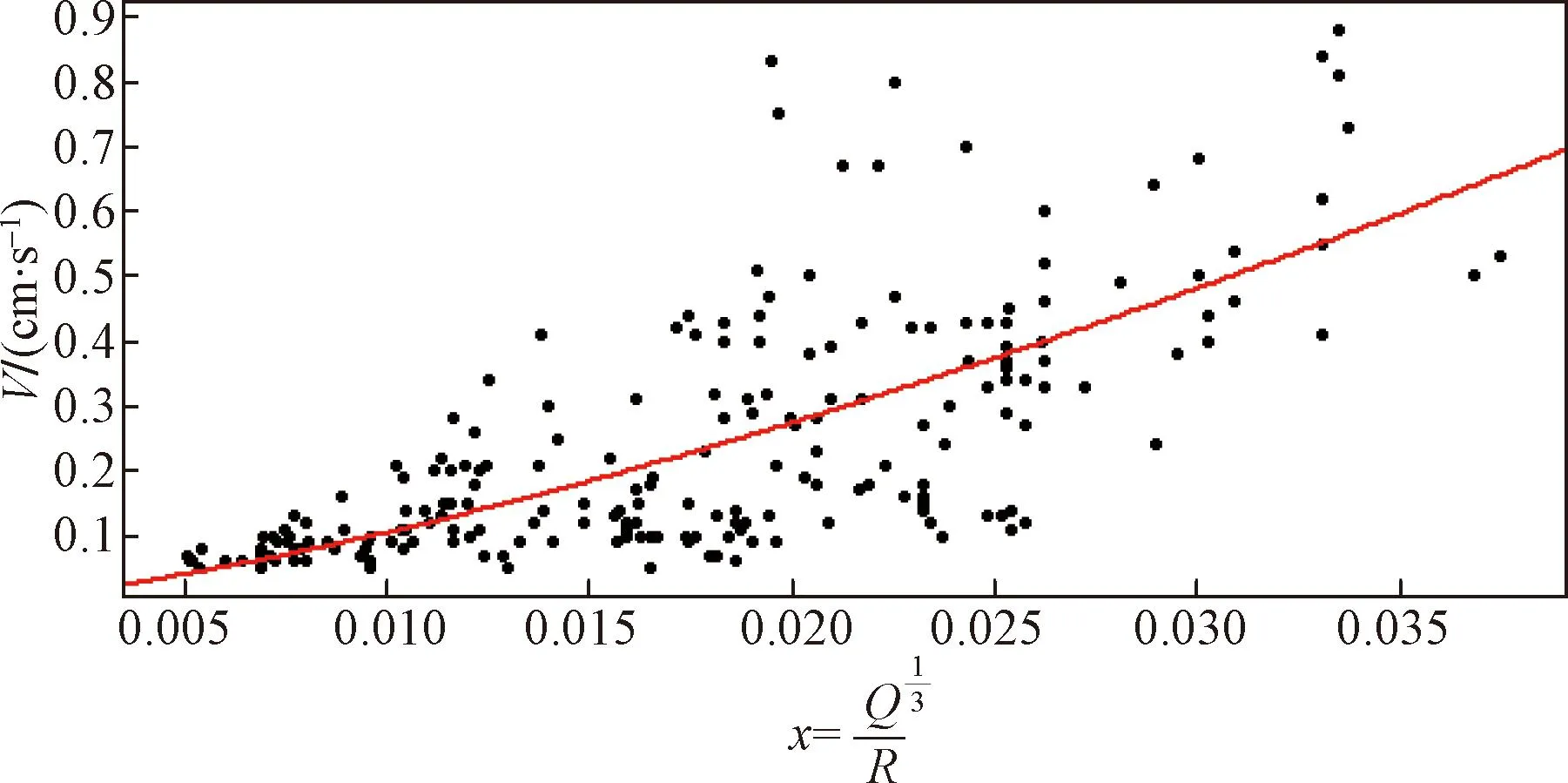
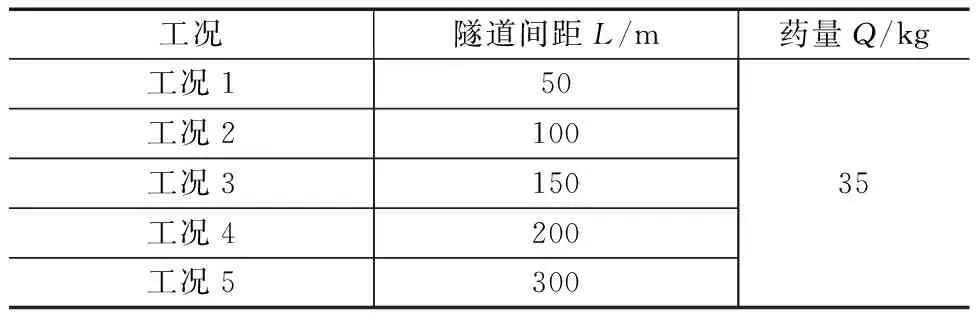
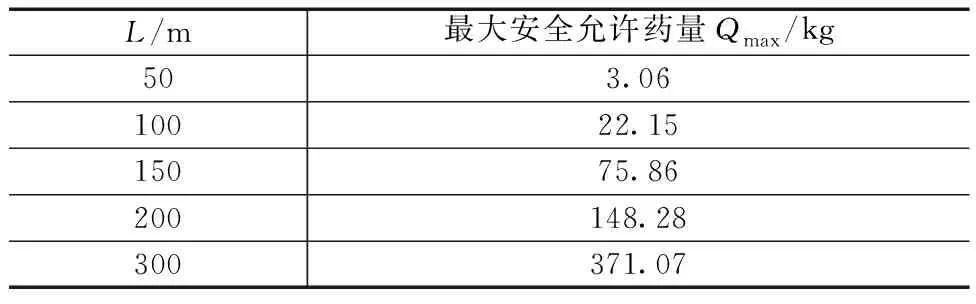
对共209组测试数据进行统计,如图2所示。统计结果显示,在对药量严格控制下,对既有线隧道爆破振动监测数据均保持在1 cm/s以下,最大振动速度0.88 cm/s,最小振动速度0.05 cm/s。其中爆破振动速度0 图2 爆破振动峰值统计 对前期监测的200余组数据进行拟合分析,得到拟合散点分布及拟合曲线(图3)和拟合回归残差图(图4)。 x为比例药量,便于线性分析;V为爆破振动速度,cm/s;Q为最大单段药量,kg;R为测点至爆破中心的距离,m图3 爆破振动经验公式拟合散点分布及拟合曲线 根据拟合结果,可计算出对应的系数K=62.74(取值范围为10.7~114.8)、爆破地震波衰减系数α=1.389(取值范围为1.167~1.61),即该项目工况下根据前期爆破振动数据的监测得到该爆破振动速度的公式为 (1) 式中:V为所测点因爆破引起的振动速度,cm/s;Q为最大单段药量,kg;R为测点至爆破中心的距离,m;K为与岩石性质、爆破方法、地形条件等因素有关的系数。 少食多餐,均匀搭配。根据患者个体性差异和身体状况,制定科学合理的运动方案,运动强度应循序渐进,定时运动。运动期间备好饼干、甜食等,避免空腹运动。 为分析新建隧道爆破掘进对邻近既有铁路隧道及铁路基础的影响,采用ANSYS/LS-dyna有限元软件,结合工程需求建立有限元计算模型进行仿真研究。为充分考虑既有线与新建隧道间距离对振动效应及规律的影响,共建立5种工况进行仿真分析,见表1。 表1 工况及对应参数 根据山体测绘得到的等高线计算机辅助设计(computer-aided design,CAD) 图处理得到山体表面的坐标,并在ANSYS软件前处理中通过APDL命令流输入各坐标点,构建得到山体模型。利用布尔操作在山体中开挖出既有隧道模型,对于爆破开挖的新建隧道同样采用布尔操作的方法,但在隧道尾部保留出部分岩体作为待爆破开挖的岩体以及掌子面。根据实际情况,在山体的后侧、左侧、右侧及底部采用无反射边界条件,并设置法向位移约束。 图5所示为工况1计算模型。新建隧道相距既有隧道50 m,新建隧道在尾部保留了部分岩体,而既有隧道则直接贯穿岩体模型;对于岩体网格的划分,根据整体模型的大小,将网格大小控制在2~10 m,并在两条隧道附近将网格进一步加密到1~4 m,使得隧道附近测点采集数据的精度更高。 图5 工况1有限元计算模型 为探究爆破振动在隧道内的传播衰减规律,沿隧道内靠近爆源一侧的拱脚位置按一定间距(68 m)取监测点进行分析,分别编号S-Z-1#~S-Z-5#。为研究同一断面不同位置处振动分布规律,取距离隧道口68 m处的隧道断面,并读取该断面上左右两侧拱脚、拱腰及拱顶5各位置的振动数据,5个测点分别编号为S-J-1#~S-J-5#。为分析隧道口基础上爆破振动的传播及衰减规律,在隧道口沿隧道轴线向外,在同一高程上每间隔16 m取1个测点,共取5个测点分别编号S-K-1#~S-K-5#。在爆破振动对铁路桥影响的问题分析中,为简化仿真,取-32 m处平面作为典型铁路桥基础平面,仅考虑爆破振动在铁路桥基础上的响应及传播,忽略桥体自身对结果的影响。根据模型尺寸的特点,在铁路桥基础上沿隧道轴线向外依次取间隔均为24 m的5个测点S-G-1#~S-G-5#进行分析。整体测点布置及相对位置如图6所示。 图6 邻近既有铁路仿真模型及测点布置 为研究爆破振动作用下路基响应规律,取隧道口处路基基础从隧道口沿轴线向外,以16 m为间距共选取5个参考点(5个测点分别编号为S-K-1#~S-K-5#)。对各工况5个测点处X、Y、Z3个方向振动速度峰值及合速度进行统计,得到表2。 表2 各测点X、Y、Z方向振动速度峰值及合速度 从以上分析可以看出,隧道口处由于距离、边界等多方面因素的影响,整体规律体现不明显,且X、Y、Z3个方向在不同测点处影响程度也不尽相同,因此建议在边界及距离影响复杂的情况下,宜对受保护对象尽可能多布置测点进行独立监测。 为研究爆破振动波对既有桥墩影响及传播规律,取隧道口平面以下32 m平面作为桥墩基面,并读取该基面上5个监测点的爆破振动数据(5个测点分别编号为S-G-1#~S-G-5#)。对各工况5个测点处X、Y、Z3个方向振动速度峰值及合速度进行统计,得到表3。 表3 各测点X、Y、Z方向振动速度峰值及合速度 同隧道口基础一样,桥梁基础处由于距离、边界等多方面因素的影响,整体规律体现不明显,且X、Y、Z3个方向在不同测点处影响程度也不尽相同,但距离最近测点还是明显高于其他点,因此建议在边界及距离影响复杂的情况下,宜对受保护桥梁基础尽可能多布置测点进行独立监测,距离爆源最近点应重点进行监测。 对各工况下的爆破振动速度进行回归拟合分析,剔除偏差较大点后,X方向拟合指标R2=0.289 6;对应回归系数a=0.235 9,置信区间为[0.003 5,0.468 3];回归基数b=-0.562 5,置信区间为[-1.513 2,0.388 2];显著性概率P为0.025 9<0.05。Y方向拟合指标R2=0.002 8;对应a=0.063 6,置信区间为[-0.477 4,0.604 6];b=-1.079 8,置信区间为[-3.325 4,1.165 7];显著性概率P为0.391 5>0.05。Z方向拟合指标R2=0.104 1;对应a=0.430 2,置信区间为[-0.114 3,0.974 8];b=0.021 5,置信区间为[-2.253 6,2.296 6];显著性概率P为0.416 5>0.05。合速度方向拟合指标R2=0.032 6;对应a=-0.115 5,置信区间为[-0.437 2,0.206 3];b=-1.436 9,置信区间为[-2.746 8,-0.127 0];显著性概率P为0.113 5>0.05。 为提高拟合程度,对各工况下的数据分工况进行数据拟合,得到5种工况下的拟合参数,见表4。 表4 各工况下拟合参数 根据表4及爆破振动公式,可计算出各工况下对应的K、α值,见表5。 表5 各工况对应的K、α取值及范围 从以上分析可以看出,将各工况分开拟合得到各工况下的拟合系数,其拟合程度整体比所有工况下的拟合效果好。基于表5对5种工况下K、α取值范围,结合《爆破安全规程》(GB 6722-2014)及铁路工程爆破振动安全技术规程(TB 10313-2019)中对K、α取值的相关规定。取工况1下K=75、α=1.22;取工况2下K=104、α=1.30;取工况3下K=128、α=1.36;取工况4下K=216、α=1.48;取工况5下K=280、α=1.51。 为得到各工况不同振速标准下的最大安全药量,可将式(1)进行转换得到 (2) 根据式(2)可计算出当控制爆破振动速度最大为V允=1 cm/s时各工况下的最大安全允许药量(Qmax),见表6。 表6 各工况下最大安全允许药量 1)通过对既有线某高速铁路隧道爆破振动的监测,爆破距离在46~263 m范围内爆破振动速度为0.05~0.88 cm/s,其振动速度均小于1 cm/s,爆破振动主频在18~256 Hz,达到了设计规范要求。 2)为研究新建隧道爆破对邻近既有隧道影响规律,构建了多工况下既有隧道爆破振动响应规律分析方案,建立了50、100、150、200、300 m共5种工况有限元仿真模型,通过加载分析,得到了既有铁路路基、桥梁、隧道在爆破振动作用下的响应规律。 3)为指导工程施工,进一步结合爆破振动经验公式对振动数据进行了拟合回归分析,得到了各工况下的爆破振动速度衰减系数K的参考值及取值范围,进而对50~300 m范围内邻近既有线隧道爆破施工最大允许安全药量进行了计算。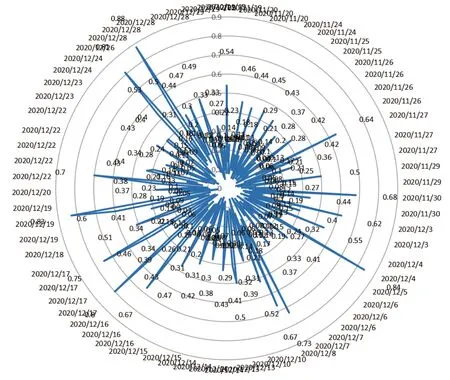
2 影响规律分析

2.1 爆破振动波对路基影响及传播衰减规律

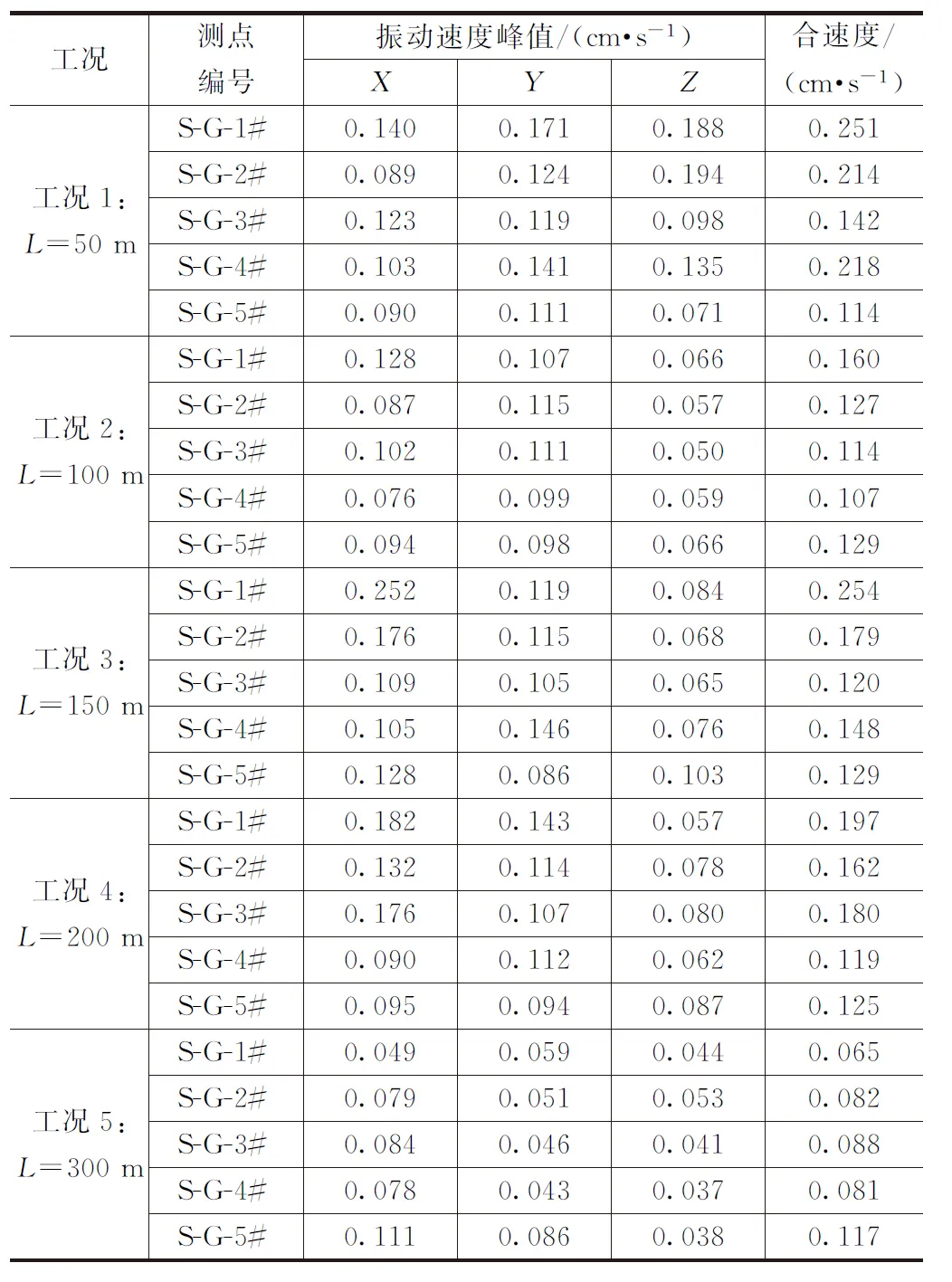
2.2 爆破振动波对既有桥梁影响及传播衰减规律
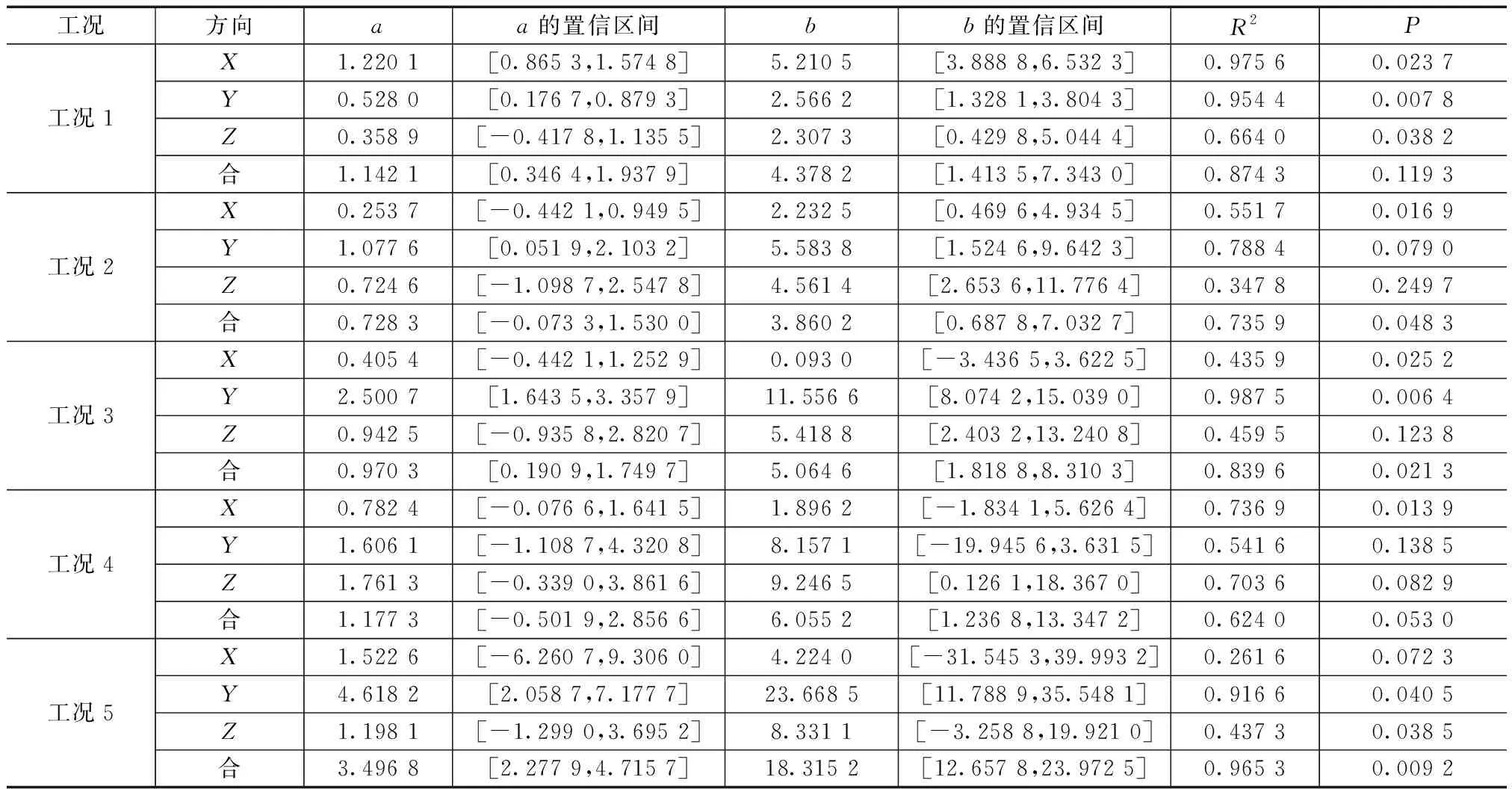
2.3 隧道爆破开挖对既有隧道影响规律数学模型
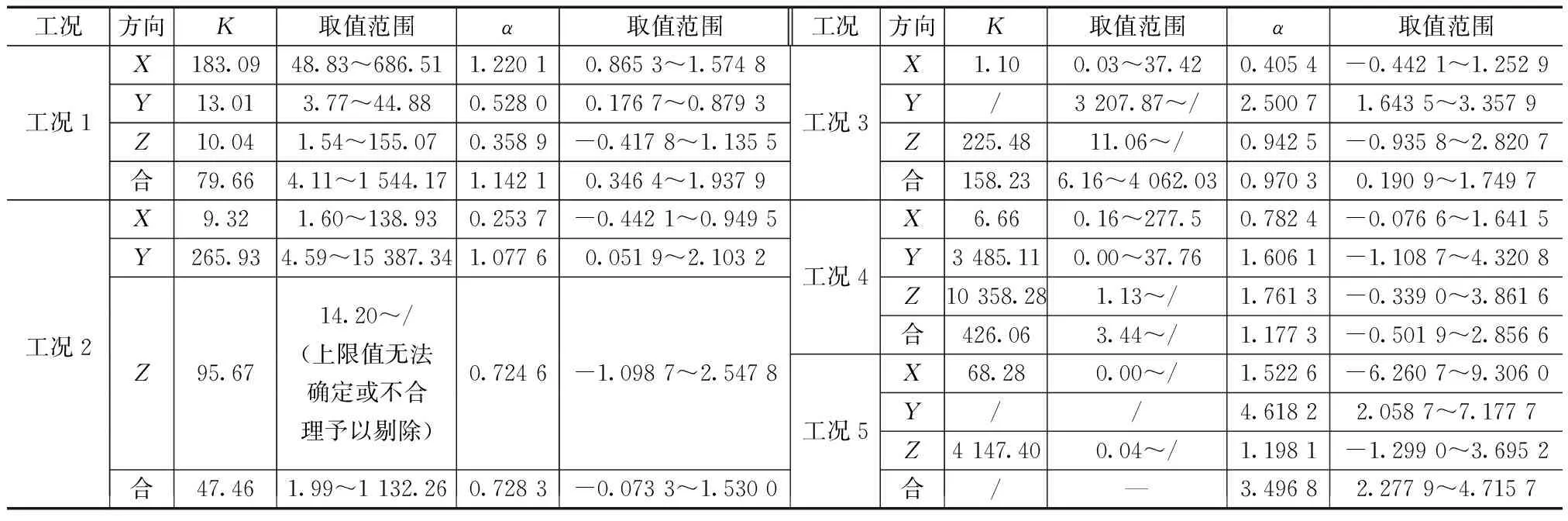
3 结论
