基于CORS 对流层延迟改正模型在山区地灾监测的分析应用

邹崇尧，梁 斌，厉芳婷，王鹏旭，林晓静

（1.湖北省测绘工程院，湖北 武汉 430074；2.武汉大学卫星导航定位技术研究中心 湖北珞珈实验室，湖北 武汉 430079）

湖北省属地质灾害多发地区，常见的地质灾害类型为滑坡。由于地灾监测预警的需求紧迫，除了直接建设单基站对各观测点进行监测外，也可利用湖北省连续运行参考站系统（HBCORS）对监测点提供虚拟参考站（VRS）数据服务，将各监测点作为网络RTK直接接入HBCORS，作为单基站监测模式的印证与补充。由于HBCORS各基准站普遍位于城市建成区与山顶、山谷的监测点存在一定高差，直接使用HBCORS进行服务时，应考虑到山顶、山谷监测点与居住建成区已有基准站之间的高差问题[1]。

为了解决监测点与HBCORS各基准站高程差导致的对流层建模精度不一致的问题，本文将利用一种改进的线性插值方法，选用GPT2+Saas 模型[2]与GMF 投影模型[3]相关参数，根据基准站与流动站之间的高程差，对天顶对流层延迟进行修正[4]，显著提升高程方向定位精度，利用HBCORS在地灾监测场景提供稳定可靠的数据服务，为CORS在普适性监测场景的应用提供了方法。

1 对流层延迟的计算

对流层延迟参数和高程参数具有很强的相关性[5-6]，在短时相对定位中，难以估计得到准确的对流层延迟，只能采用外部改正[7]，在实际应用中，通常使用一些对流层延迟算法来建模实现外部改正。

1.1 常规对流层延迟的计算

对流层延迟可以根据基准站间计算的大气来内插流动站处的大气信息，常用的是基于平面二维坐标线性插值法（LIM）来计算。

式中，o为基准卫星；p为参考卫星；1、2…n-1为用到的辅助基准站；∆X和∆Y分别为2个站在X方向和Y方向上平面坐标的差值；̂计算的是双差对流层延迟；a、b为内插系数，通过最小二乘法可表示为：

那么流动站v 与主基准站M 之间的双差对流层延迟方程为：

式中，为基准站M 与流动站V 之间依据卫星；o、p内插得到的双差对流层延迟。

1.2 对流层延迟的改进算法

对流层延迟受观测设备位置影响很大，基准站与流动站存在较大高差时，双差对流层延迟的不准确性会直接导致测量误差的增大，且对于类似情况的基准站网，这个误差为系统性误差。

为了解决这个问题，本系统利用了一种改进的线性插值法。在对任意2 个高差较大的基准站进行区域大气建模时，提取完固定基线下的双差大气信息后，首先完成对流层延迟的高程偏差补偿修正，下面将进行具体阐述。

某个三角网存在3个基准站M、N、B，此时有接入的流动站V，且距基准站M最近，则M为三角网主基准站，N、B为辅基准站，在利用LIM法计算该内插模型前，站M和站N之间的双差对流层延迟应为：

式中，∆hMN为基准站M 与基准站N 之间的大地高之差；(∆hN)和(∆hM)分别基准站N 与M 同卫星o、p 的星间单差对流层延迟；hM、hN为站M、N 大地高。将基准站的高程补偿至流动站大地高椭球面hV，则基准站M和N经过补偿后的单差对流层延迟分别为:

方程（6）、（7）的补偿改正值可进一步推导为：

方程（8）、（9）进一步展开可得：

式中，ZTDM(hV)为基准站M在hV高程下的天顶对流层延迟，可利用GPT2+Saas 中相关大气参数计算；MFpM(hV)为基准站M在hV高程下卫星p投影函数，可利用GMF相关参数计算，其余近似表达含义一致。相对于基准站M、N 校正前存在的对流层延迟系统误差，通过在同一水平面hV，使用传统的LIM方法也可获得高校正精度的对流层延迟修正值TCorM、TCorN。

将方程（6）、（7）、（8）、（9）代入方程（5），则方程（5）可表示为：

式中，(∆hVV)为修正后的基线MN基于基准卫星o与参考卫星p的双差对流层延迟。

将这项系统性的双差对流层延迟进行提前修正后，再利用传统LIM方法进行内插，则可以得到任意2 个站点不受高差影响的双差对流层延迟。这个过程即为MLIM方法。

2 研究区域介绍

本文将以HBCORS在鄂西地区的基准站作为实验分析对象，验证对流层的改进算法，从而分析地灾监测点接入HBCORS时的情况。

鄂西地区一般包括十堰、恩施、襄阳、宜昌4 个地市、神农架林区以及荆门、荆州市部分地区，经度分布大约在108°~112°E 之间。根据HBCORS 概略分布及高程统计图（如图1），可见鄂西地区基准站普遍高程在200~600 m，部分基准站高程达到900 m以上。

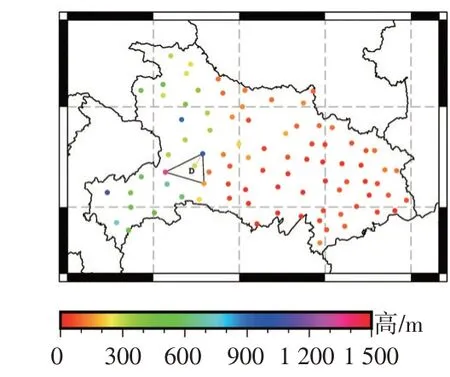
图1 HBCORS概略分布及高程统计图

具体选取鄂西地区存在较大高差的相邻基准站4 个，取外围3 个站作为基准站组成三角网，三角网内部基准站作为流动站进行观测并获得固定解，该实验网型、站间距、各站高程如图2、3所示。通过采用传统LIM 与MLIM 2 种方法可内插出不同对流层建模策略下的流动站大气延迟，进而可以生成2 种虚拟观测值，发送给流动站进行RTK对比测试，

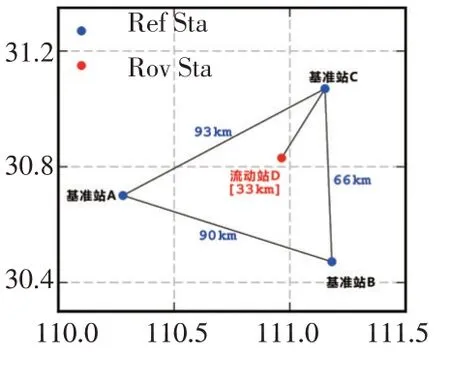
图2 实验网分布 及基线示意图

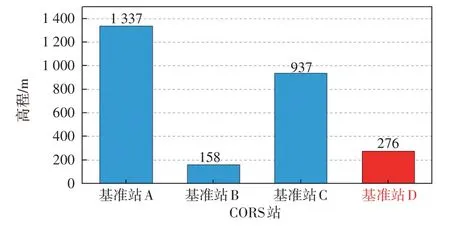
图3 实验网高程分布统计图

3 实验结果及分析

由于图2 中选择的模拟流动站实际为坐标精确已知的CORS 基准站，因此站点的RTK 结果可以直接进行外符合精度比较。通过收集原始观测数据，整理后对定位误差与固定率等指标进行了统计，并绘制了站点D 在LIM 模式与MLIM 模式下的外符合定位误差时间序列（如图4）。

从统计与图4 的结果可以得出：①流动站D 在LIM 与MLIM 方法下的RTK 固定率均比较高且没有呈现出太大的差异，固定率分别96.6%与99.9%；②2种方法的水平定位误差分别为E：2.7 cm、N：3.2 cm 与E：0.7 cm、N：0.8 cm，MLIM方法在E方向上的精度提升为74%、在N 方向上的精度提升为75%；③传统LIM 方法在高程方向呈现出了明显的误差，U 方向的定位误差RMS为34.3 cm，MLIM方法定位误差RMS仅为2.2 cm，相比较于LIM的精度提升为93.6%。

在U 方向上的定位误差RMS 上的差异，显然是由于传统LIM 方法在未考虑基准站与流动站之间存在的高差给对流层建模带来的影响，从而为流动站引入了较大的建模残差导致，MLIM 方法则全面考虑了高程对对流层建模的影响，因而在U 方向上的定位精度较高。

根据本实验数据，若需要进地灾监测的区域大地高与附近的HBCORS 基准站大地高存在较大高差时，有必要在对流层建模时利用MLIM 方法进行对流层延迟的修正，从而降低鄂西地区各类监测站点使用HBCORS 时生成的额外大地高误差，达到进行地灾监测所需的精度要求。

4 结 语

本文利用MLIM 方法，改进了HBCORS 生成VRS时对流层延迟的计算方法，全面考虑了高程差对对流层建模的影响，显著提升了高程方向的定位精度，经实验验证，高程方向的定位精度提升可达93.6%。本方法满足了山区利用基准站网开展地灾监测的需求，降低了大量的监测站接入时的单基站系统布设压力，为各基准站网开展山区普适性地灾监测提供了解决方法。