基于层次格网索引的高程点线矛盾快速识别方法
2024-01-09刘康甯王方民杨孟翰
刘康甯,叶 胜,王方民,杨孟翰,陈 林
(1.重庆市地理信息和遥感应用中心,重庆 401147)
数字地形图的生产过程中,仪器误差、系统误差、人工粗差及数据转换等多种因素均可能导致高程点与等高线的高程值间出现逻辑矛盾[1-3]。高程点线矛盾作为数字地形图的重要质量因子,解决这一问题是进行质量控制的关键环节[4-5]。点线矛盾的解决能够有效提升高程数据的精度,为高程数据及衍生产品生产与分析、实景三维构建、土石方工程量算、长时间序列地形变化研究等应用提供更高精度的基础数据,充分发挥数字地形图中高程信息的应用价值。
本文针对当前高程点线矛盾检查中存在的关键问题,提出了一种利用层次格网索引(hierarchical grid index,HGI)数据管理模式,与多进程并行机制相结合的高程点线矛盾快速识别方法,并通过充分梳理点线矛盾错误类型及高程点线空间位置关系进一步完善高程判断逻辑,优化提升了识别方法的准确性和特殊地形下的适用性。
1 数据及错误类型
1.1 高程点线数据
本文选用从重庆市酉阳县1∶10 000 国家基本比例尺地形图中提取的高程点及等高线数据作为测试数据,等高距为5 m。等高线具有等值性、局部闭合性、连通性和高程递变性等特征[6]。等高线连续且具有相同等高距D是高程点线矛盾检查的必要条件[7],因此从地形图中提取了等高线的首曲线和计曲线,并消除了等高线自身的高程冲突问题,同时为测试在参照信息不全等特殊情况下,算法对高程数据点线矛盾的识别效果,未对数据中存在部分缺失的等高线进行补全。
1.2 点线矛盾类型归纳
受现实地形多样性、复杂性影响,高程点数据呈随机分布特征,点线矛盾在空间分布上不具有明显规律性。从错误类型上来看,点线矛盾多为人工粗差,可进一步可归纳为:①高程逻辑冲突(图1a);②点线重合(值相等/值不相等)(图1b)。
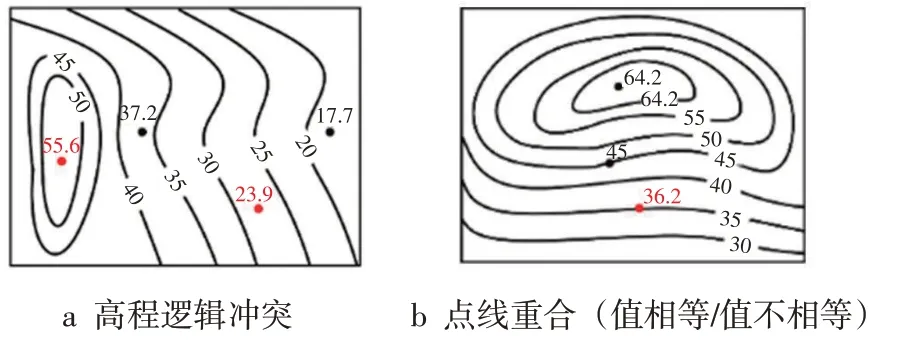
图1 点线矛盾类型归纳示意图
2 研究方法
2.1 层次格网索引
空间索引是指依据空间对象的位置和形状,通过建立数据逻辑与存储空间的对应关系来描述空间数据在存储空间中位置的一种数据结构,良好的空间索引能够大大加快空间数据的处理速度[8-9]。层次格网索引(HGI)是对整幅空间数据进行k次划分(即k层),得到k层mk*nk(mk:k层行数,nk:k层列数)的数据结构,每个网格区域为一个索引项,并分配一个动态存储区,满足划分条件的地理数据被存储到对应的存储空间中[10-11]。由于数字地形图在生产和管理中均采用图幅为基本单位,高程点线要素和在二维空间中表现出受图幅约束的规律性分布状态,采用层次格网索引能够更加灵活高效的进行数据组织和数据管理。
面状格网要素以图幅信息为依据,通过ArcGIS中的创建渔网工具生成图幅对应的面状格网数据,赋予每个面状格网要素对应的图幅编号属性信息。面状辅助格网数据在高程点线矛盾识别过程中,作为传递图幅长宽尺寸数据的重要介质。
本文采用三层层次格网来构建索引关系(图2),结合数字地形图分幅管理模式及矢量高程要素图形属性关联方式,分别设计了第一层和第三层空间,同时为解决点线矛盾运算的数据遍历机制在应对大数据量时效率低下的问题,使用数据精细化管理的思路,从内部结构上精简参与运算的数据量进而降低运算压力,设计层次格网索引中间层,并设置了开放参数,用于中间层空间的精细化约束:第1 层以图幅编号作为索引标签,利用等高线及高程点图幅编号属性进行单元划分;第2 层依据当前图幅的面状辅助格网数据最小外包矩形(MBR)按照式(1)可以获取3个关键参数(左下角坐标P0(x0,y0),长度步长∆L,宽度步长∆W),以上述参数为基础将第2 层空间分割为m2×n2个小单元,同时构建要素在HGI第二层空间中的存入方式,点状要素按照式(2)获取对应的行列号,等高线环要素根据其MBR 中心点坐标按照式(2)获取行列号,图幅内部的等高线总体通过与HGI第2 层的单元进行求交,当存在相交关系时进行存入;第3 层将第2 层索引中单个要素的图形及属性分离存储。
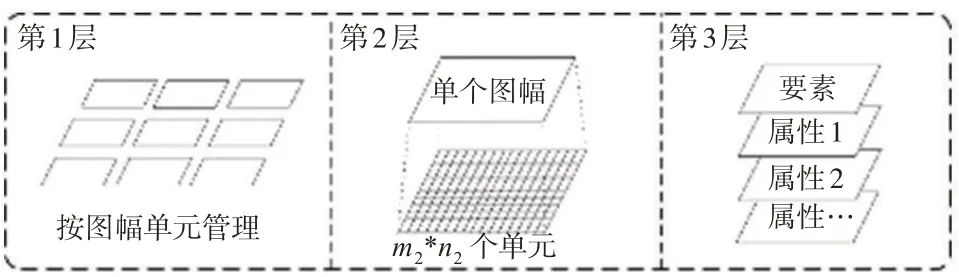
图2 HGI模型设计
式中, MBRGrid为面状辅助格网要素的最小外包矩形;Length 和Width 分别为MBR 的长宽属性值;m2为HGI中间层空间分割行数;n2为HGI中间层空间分割列数。
式中, row 和col 分别为HGI 第2 层空间中的行列号;x和y分别为参与计算的点坐标X和Y的值。
2.2 点线矛盾判断逻辑
基于高程点与等高线的空间位置关系进行点线矛盾判断逻辑构建,如图3 所示,高程点P 及等高线L1、L2、L3 的高程值分别为EP、EL1、EL2、EL3,等高距为D,L1 为高程点P 的最邻近等高线,L2 为第二邻近等高线,L3 是第三邻近等高线,将高程点与等高线间的逻辑关系抽象概括为如图3所示4 种情况,归纳出不存在点线矛盾时应满足以下条件:
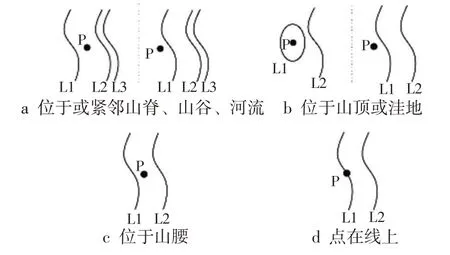
图3 高程点线空间位置关系
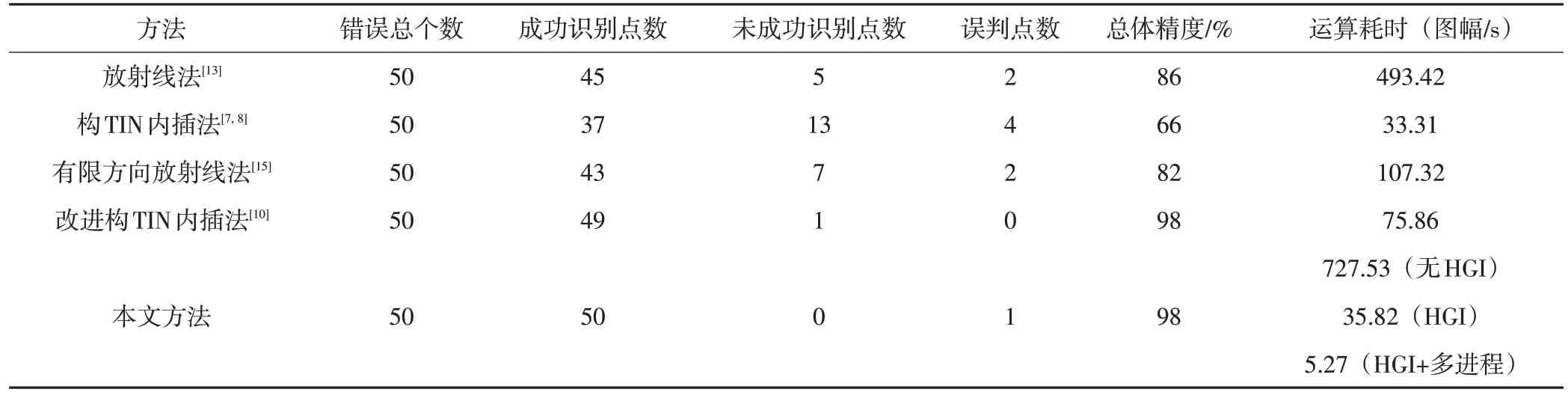
1) 当EL1=EL2≠EL3时,高程点位于或紧邻山脊、山谷、河流,其空间位置关系如图3a,此时,若EL2>EL3,则高程点位于或紧邻山脊,应满足:(EP-EL1) 2) 当EL1≠EL2,且P点及L2上最近点构成线段与L1 相交时,高程点位于山顶或洼地(图3b),若EL1>EL2,则应满足:0<(EP-EL1) 3) 当EL1≠EL2,且P 点与L2 上最近点连成的线段和L1 不相交时,高程点位于山腰(图3c),若EL1>EL2,则 应 满 足: (0<(EL1-EP) 除上述情况外,部分高程点落在等高线上(图3d),形成点线重合,点线高程应保持一致,此时,若满足:EP=EL1记录为位置异常,否则记录为点线矛盾。 运算效率是算法性能的重要指标,高程点线数据均为空间数据,相较于文本数据,空间图形数据的计算往往会造成更多的运算耗时,通过对本文算法特征及常规并行方法的分析,本方法为CPU 密集型而非IO 密集型,多进程机制能够更好的进行运算效率优化提升。本文方法在多进程机制下的算法流程如图4所示。 图4 算法流程图 本文方法针对构TIN 内插法对平三角处的局限性,以及放射线法运算效率偏低等问题进行了改进与完善,为进行算法测试和精度、效率比对,基于python 与arcpy 站点包进行方法实现,利用配置为AMD 16 核处理器、64 G 运行内存的计算机开展试验与结果分析。从重庆市酉阳县1∶10 000 国家标准比例尺地形图中选取9 个图幅(303 图幅范围:左上角起始图幅编号H49G075014,右下角终止图幅编号H49G077016)的矢量高程数据作为测试数据,测试数据共计22 142 条等高要素,5 010 个高程点要素,每幅图幅平均等高线要素数为2 460 条,平均高程点要素数为557 个,酉阳县地处武陵山区腹地,河流水系发达,是典型的喀斯特山区,多断崖和落水洞发育,地形地貌复杂度高,矢量高程数据错误类型多样,测试数据中共包含高程点错误50 个,用于精度测试。同时根据测试数据点线要素分布特征,本方法中HGI 中间层参数m和n均按16 取值,各方法测试结果如表1所示。 表1 不同方法对高程点线矛盾识别效果对比 识别精度方面:由表1 可知,放射线法的识别精度为86%,存在5个未成功识别的错误高程点,其中3个高程点为凹山顶,2个高程点处于河流处,另将2个临近问题等高线(部分缺失)的正确高程点误判为错误高程点;由于构TIN内插法仅能对非平三角区域的高程点数据进行判别,总体精度为66%,未成功识别的高程点有13个;其中2个为点线重合且高程值不相等,2个位于河流处,凹山顶处高程点3个,1个高程点临近问题等高线(部分缺失),另有5个山腰处的错误高程点未被成功识别,同时构TIN 内插法还将4个位于数据边缘处的正确高程点误判为错误高程点;本文方法对50个错误高程点均进行了有效识别,但因缺少可参照高程信息,将1 个处于河流内且位于数据边缘的正确高程点误判为错误高程点,总体精度为98%。 运算效率方面:由于构TIN 内插法需要人工参与,无法实现全流程的自动化识别,因此不进行对比;放射线法的运算耗时为493.42 s,由于本文方法使用了更加细致的判断逻辑,在未使用HGI索引的情况下,单个图幅运算耗时为727.53 s,通过添加HGI索引,耗时优化为35.82 s,并行机制下(8 个进程)运算耗时进一步优化为5.27 s,运算效率较无索引且非并行状态下提升2 个数量级(1/138)。可见HGI 对效率改善有着十分积极的作用,同时能够充分结合多进程机制,实现运算效率的大幅提升。 文献[9]对构TIN 法进行了优化,文献[10]对常规放射线法进行了优化,利用上述优化方法进行算法实现和数据测试,并与本文方法进行对比分析,文献[9]方法的错误识别精度与本方法相同,50 个错误高程点中,处于图幅边缘处的1 个错误高程点因可参照高程信息缺失导致内插等高线出现错误,错误高程点未能有效识别,同时该方法在应对较大数据量时,其反复构TIN 过程会引入较多耗时,运算耗时75.86 s。文献[9]提出的有限方向法在提高运算效率的同时降低了对错误高程点的识别精度,共有7 个错误高程点未能成功识别,其中4 个位于山腰处,1 个位于河流处,另有2 个为点线重合且高程值不相等,此外由于检索方向的减少,在图幅边缘处有2 个高程点出现误判现象,总体精度为82 %,运算耗时107.32 s。本方法所采用的HGI 索引数据管理模式和多进程的运算机制能够在平衡精度和效率方面有着更好的表现。为进一步测试方法的适用性与可靠性,从重庆市1∶10 000 基础库中随机抽取9 个图幅进行高程点错误检查,通对比统计,本文方法对测试数据中存在的39 个错误高程点全部实现成功识别。相较于现有方法,本文方法在精度、效率、适用性方面表现良好。 本文将层次格网索引应用到高程点线矛盾检查的过程中,进行并行机制设计,同时对点线矛盾错误类型及高程逻辑进行充分分析,结合等高线的空间位置关系完善判断逻辑,在提高判断精度的同时大幅提高了运算效率。2.3 算法流程及多进程并行机制
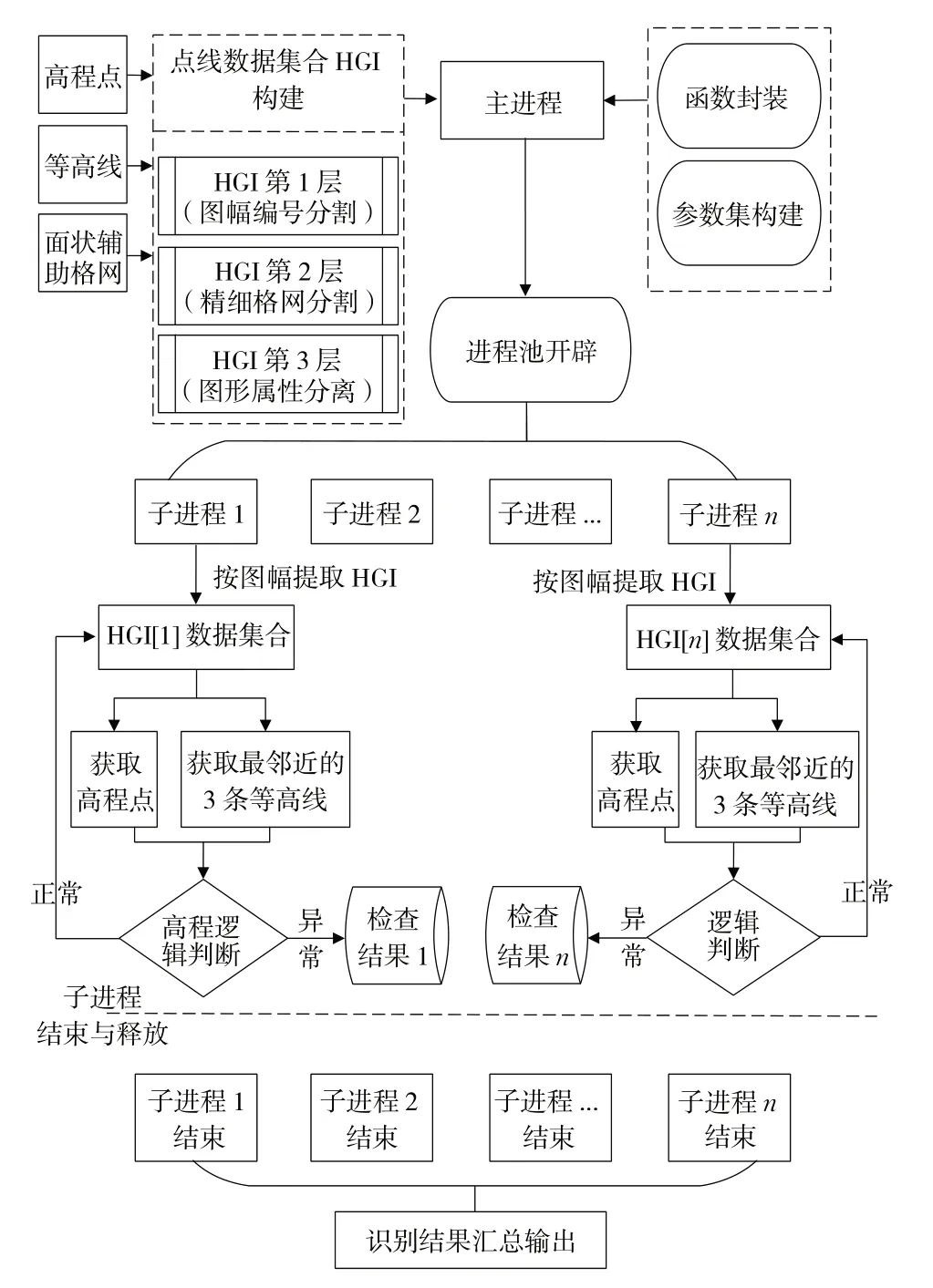
3 试验与分析
4 结 语
