AFBCNet:一种基于自适应滤波器组的运动想象卷积神经网络*
2024-01-09申佳华代成龙李光辉
申佳华,代成龙,李光辉
(江南大学人工智能与计算机学院,江苏 无锡 214122)
脑-机接口技术(Brain-Computer Interface,BCI)历经三十多年的发展,逐渐架起了人与外部设备沟通的桥梁[1]。BCI 系统可以分析人脑的神经活动,然后通过解码技术让人类能够操控外部设备或者与外部直接通信。其中,基于脑电信号(Electroencephalogram,EEG)的BCI 得到了最广泛的应用,主要原因是非侵入式的EEG 信号采集成本相对较低、安全无创,且基于EEG 的BCI 便于安装与携带。目前,BCI 技术的应用主要包括:①帮助病人进行身体康复,比如中风患者[2];②监测人体状况[3];③运动神经受损人群的器官替代,比如操控轮椅和假肢[3];④为健康人群设计辅助功能,比如人体增强[4]。可见,BCI 系统有着非常广泛且有前景的应用,而EEG 的解码技术成为了影响BCI 发展的主要因素之一,尤其是基于运动想象(Motor Imagery,MI)[5]的EEG 解码。
MI-EEG 信号的解码与分类问题是BCI 领域最具有挑战性的任务之一[6]。现有的MI-EEG 的分类方法主要分为传统的机器学习方法和深度学习方法,其中基于深度学习的方法在近年来逐渐超越了传统机器学习方法,成为了MI-EEG 分类中最具前景的研究方向之一。
传统的机器学习方法通常由信号的预处理、特征提取和特征分类三个部分组成。在信号的预处理阶段,通常会采用带通滤波器、典型相关分析(Canonical Correlation Analysis,CCA)[7]或者独立成分分析(Independent Components Analysis,ICA)[8]等技术对MI-EEG 信号中的伪迹进行剔除,从而提高信噪比。在特征提取阶段,目前的研究主要集中在空间滤波和黎曼几何(Riemannian Geometry,RG)协方差学习上,比如共空间模式(Common Spatial Pattern,CSP)[6]、滤波器组共空间模式(Filter Bank Common Spatial Pattern,FBCSP)[9]等。在特征分类阶段,主要使用线性判别分类器(Linear Discriminant Analysis,LDA) 和支持向量机(Support Vector Machine,SVM)等方法进行分类。尽管基于CSP 以及其改进的方法能够得到不错的结果,并且能够进行快速训练和相对简单的部署,但是传统的机器学习方法的特征选择过程非常依赖专业的先验知识,并且这类方法通常会造成特征丢失和节律退化。
近年来,随着深度学习在许多领域取得了很好的成绩,BCI 领域的研究人员也开始积极地探索适合于MI-EEG 的解码网络的设计方法。Li 等[10]将α(8 Hz~13 Hz)和β(13 Hz~30 Hz)频段划分为10个时间窗口和3 个子带,然后对每个子带的时间窗口求平均功率,因此每个电极都获得了多个平均功率作为时频特征,其次通过插值算法将其排列到电极坐标图上,得到一组复杂的特征图,最后输入改进的VGG 网络进行训练。DFFN[11]采用CSP 进行空间滤波,然后计算时域对数功率并作为特征输入类似于DenseNet 的网络进行训练。Sakhavi 等[12]基于FBCSP 算法和通道卷积,提出了通道混合模型来提取了脑电信号的时空特征。Tabar 等[13]使用短时傅里叶变换重构了脑电数据的时频二维图像,然后输入堆叠式自编码器进行训练。Zhao 等[14]结合强化学习和图卷积方法来提高性能,采用深度强化学习来自动预测给定的大脑网络所需的最佳特征传播次数,提高了网络的泛化能力。RTGNN[15]使用张量分解来提取公共特征空间中每个视图的图结构特征,并且通过强化学习过滤不相关的邻居节点以提高性能。Schirrmeister 等[16]受到FBCSP 算法设计理念的启发,提出了一种时空双步卷积(先时域卷积提取特定频带信号,然后空间卷积提取空间特征)的浅层解码网络ShallowNet,通过时空滤波器分解MIEEG 信号,并且在MI 数据集上与传统的方法相比具有更高的精度。EEGnet[17]借鉴了时空双步卷积的思想,提出了一种通用的轻量化网络模型,尤其是在空间卷积上采用了Depthwise 卷积,对特定频带的信号逐层空间卷积,使信号得到进一步的分解。TCNet[18]在EEGnet 的基础上引入了时域卷积网络(Temporal Convolutional Networks,TCNs),进一步挖掘双步卷积后的时域特征,并用验证了TCNs 的有效性。上述几种基于时空分解的神经网络模型在进行时域卷积时,使用的是传统的卷积层,但是传统的卷积层通常会聚焦于低频部分而不善于学习窄带信息。FBCNet[19]借鉴了FBCSP 的频带划分模式,将4 Hz~40 Hz 的频段划分为9 个子频带来取代传统时域卷积CNN,模型无需通过卷积层学习如何提取特定频带信息,并且利用方差层来进一步挖掘时空分解后的时域特征,然而这种方法会带来频带切割的固化,从而不利于分解MI-EEG 信号。Zhao 等[20]利用领域迁移的技术,同时训练了分类器、特征提取器和领域识别器,联合优化了中心损失、对抗损失和分类损失。Zhang 等[21]提出了一种类似于Inception的结构,并进行堆叠,使用多尺寸的卷积核提取特征,并通过添加高频噪声提升模型的性能,虽然这种Inception 模块具有良好的性能,但是过大的卷积核也会造成参数量过多和过拟合的问题。
综上所诉,为了解决传统卷积层时域卷积存在的缺陷和频带组合模式固化问题,本文改进了时空双步卷积过程,在时域卷积上采用了一种自适应的矩形滤波器,这种方法可以让模型自主学习最优频带组合,通过对矩形带通滤波器设计的先验知识,用较少的参数,使得滤波器的学习更加容易、收敛更加快速。这种自适应的分解方式可以很容易地应用到不同的受试者,并且对于不同的受试者,可以学习到不同的滤波器组。为了解决Inception 结构的参数过多与过拟合问题,本文结合了深度可分离卷积(Depthwise Separable Convolution,DSC)和膨胀卷积的方法改进Inception 结构,既保持了性能也减少了参数数量。此外,目前大多数研究都集中在二分类任务上(如BCICIV_2b 数据集[16]),多分类任务的研究进展较为缓慢且大多数四分类算法的精度偏低(如BCICIV_2a 数据集[16],平均精度通常在68%~78%),还不足以应用到实际场景且不足以进行轻量化设计与部署。相比于近年来的先进方法,本文所提出的基于自适应滤波器组的运动想象卷积神经网络(Adaptive-Filter-Bank Convolutional Network,AFBCNet)极大地提高了模型的可解释性与精确度。
本文剩余部分的行文结构如下:第1 章介绍本文所用到的方法和技术。第2 章介绍所提出的模型。第3 章介绍实验设置、开展实验与分析讨论。第4 章为总结。
1 相关方法简介
1.1 深度可分离卷积
传统的卷积神经网络在图像分析、自然语言处理等领域取得了非常优异的成绩,通常使用深层、多尺度的卷积层来提取浅层到复杂的特征信息。卷积神经网络采用局部连接的方式来代替矩阵的乘法运算,从而降低了计算成本,同时也得到了更好的性能。给定输入Xc+i-1,t+j-1,m(尺寸为C×T×M),传统卷积核Ki,j,m,n(尺寸为Ck×Tk×M×N)的运算公式为:
然而,同时在一个计算步骤中整合空间和通道信息的计算量也依然较大。因此,基于拆分运算思想的DSC 应运而生。与传统卷积不同的是,DSC 将卷积运算分成了两个简单卷积运算,即先做DC(Depthwise Convolution)运算,然后做PC(Pointwise Convolution)运算。DC 对每个特征层分别使用一个卷积核,然后将所有卷积核的输出拼接叠加在特征层维度。因此,DC 运算没有整合通道上的特征信息,而后的PC 运算就可以弥补这个缺点。PC 实际上就是(1×1)的传统卷积,这主要起到了两个作用:①能够自由地改变通道的数量;②能够对DC 输出的数据进行通道信息整合。DC 和PC 的运算公式分别为:
式中:和分别是DC 卷积核与PC 卷积核,Xc,t,m和Xc,t,n是DC 运算和PC 运算的输出。因此,DSC在运算效率和参数规模上都远远优于传统卷积。
1.2 自适应滤波器组
传统的时域卷积很难应对MI-EEG 数据的低信噪比、训练样本少和学习难等问题,并且学习到的滤波器包含很大的噪声,而自适应滤波器组(Adaptive Filter Bank,AFB) 能够解决传统卷积带来的问题[22]。首先通过对滤波器形状的先验知识,构造矩形带通滤波器g[t,f],其中f代表少量的可学习参数。g[t,f]的频域特性可以表示为两个低通滤波器的差分运算:
式中:rect(·)代表矩形函数,f1、f2分别是可学习的低截止频率和高截止频率。G[f,f1,f2]经过逆傅里叶变换得到其时域的表达式为:
式中:截止频率的初始化范围为[0,fs/2](fs为采样频率),且f2≥f1≥0。因此,通过先验知识设计的滤波器g[t,f1,f2]是可微分的,可以与深度学习模型中的其他参数一起进行传播优化。最后,由于g[t,f1,f2]的离散近似特性,AFB 得到的带通滤波器是非理想的且可能在通带产生波纹,在阻带产生有限的衰减。因此,为了平滑g[t,f1,f2]的截断特性,在g[t,f1,f2]上乘上汉明窗口ω[t],其表达式为:
式中:a0=0.538 36[22],L为窗口长度。因此,给定输入MI-EEG 信号X[t],其运算过程为:
1.3 Inception 模块
随着深度学习的研究与发展,深层的模型已经逐渐遍布各个研究领域。虽然深层的模型能够拟合任何连续函数,但是随着层数的加深,模型会出现过拟合、梯度消失、模型性能停滞、内存开销大等问题。因此,Inception 模型的初衷就是为了解决卷积神经网络的性能问题和计算内存开销问题。
Inception 模块通过并行不同尺寸的卷积核和池化层来提取特征,并且通过(1×1)的卷积核来减少通道数量。计算机视觉中,最常用的卷积核为(3×3)和(5×5)。在MI-EEG 分类研究中,Inception 结构最常用的卷积核为(1×25)、(1×75)与(1×125)[21],但是这也带来了巨大的计算量和内存开销,并且在小样本的MI 数据集上很容易过拟合。因此,如何改进Inception 结构让其适用于MI-EEG 的分类任务成为了一个难点。虽然Inception 从提高性能和减少计算量的角度提出了分解卷积核和空间分解非对称卷积等方法,但是这在MI-EEG 上很难适用。本文所提出的通过膨胀卷积和DSC 等方法来改进Inception 模块成为了一种新的解决方案。
2 AFBCNet 框架
本文提出了一种基于自适应滤波器组的卷积神经网络,其四分类任务的网络框架如图1 所示(以BCICIV_2a 数据集为例),网络详细设计参数如表1 所示。AFBCNet 主要包括三个模块:①信号分解模块;②Inception 时域特征提取模块;③特征整合及分类模块。
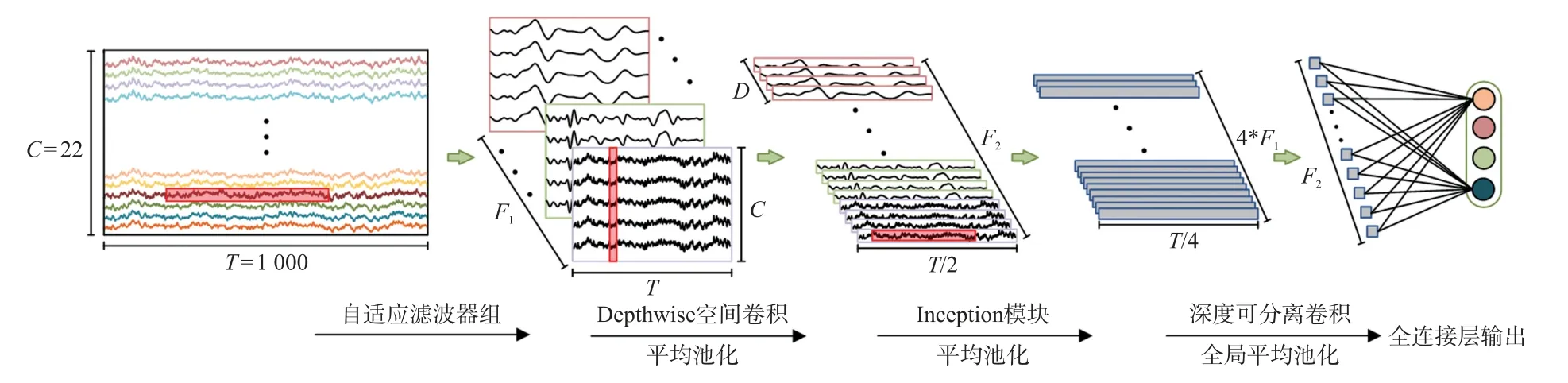
图1 所提出模型的网络架构示意图

表1 AFBCNet 网络设计框架
首先,信号分解模块借鉴了EEGnet 的时空双线性分解技术[17]和FBCnet 的频带切割策略[19]。因此,该模块由AFB 和Depthwise 空间卷积两部分构成。AFB 通过对滤波器形状的先验知识规定了卷积核的频率特性,从而降低了模型的学习难度,因此更加适合小样本的MI-EEG 数据集。第一步,AFB 通过F1个(1×16)的卷积核沿着原始MI-EEG信号E(E∈RC×T)的时间轴进行卷积,提取出F1组最优频带的MI-EEG 序列。第二步,Depthwise 空间卷积层对第一步时域分解得到的F1层最优频带的特征图分别做D次空间卷积,卷积核大小为(C,1)。这种时空分解的方法能够让特定频带的信号得到多个空间滤波器,同时可以灵活地调节时空分解的粗细程度。此外,本文在每组滤波器后面增加批量归一化层加快收敛,并在信号分解后采用平均池化来减小时间维度。
其次,本文利用改进的Inception 结构进一步提取信号分解模块得到的多频带时域信息,其网络结构如图2 所示。虽然很多研究者尝试使用不同的方法提取时空特征提取后的多频带时域信息,如TCNs[18]、方差层[19]等,但是在MI-EEG 分类上的性能提升有限。本文借鉴Inception v3 的设计思路并且结合深度可分离卷积与膨胀卷积来改进Inception结构。相关研究表明[21],较大尺度的卷积核更有利于提取MI-EEG 信号特征,但是这也会带来很多问题,比如参数过多、容易过拟合等。为了解决这些问题,本文采用DSC 来替代传统的卷积核,并且通过将较大的DSC 卷积核拆分成两个较小的DSC 卷积核的方式来减少参数量和运算。但是这种做法也带来了感受野减小的问题。因此,本文在第二个较小的DSC 卷积核上加上膨胀系数,使得感受野扩大到原来的平方倍。此外,本文在两个较小的DSC 层之间加入批量归一化层和ELU 激活函数,并且在特征图拼接之前,采用平均池化进一步减小时间维度。
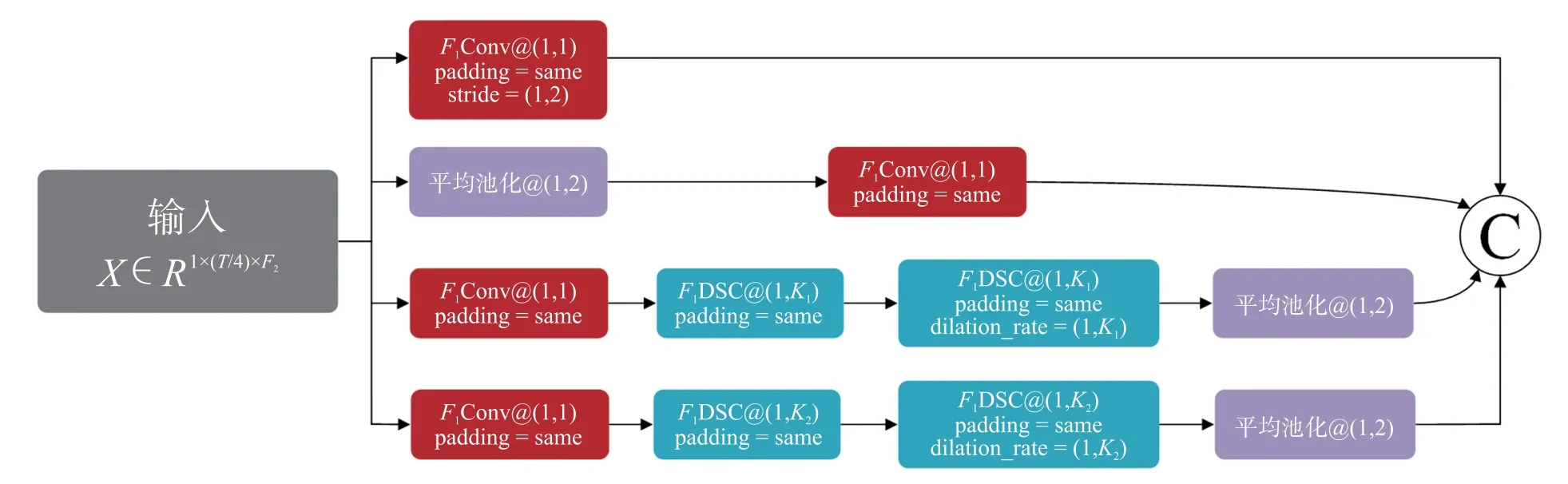
图2 改进的Inception 网络结构示意图
最后,本文通过一层DSC 来整合Inception 模块提取到的特征,并用全局平均池化将数据特征降维到F2个特征点。为了避免过拟合以及减少计算复杂性,网络中没有添加额外的全连接层,而是直接将F2个特征点输入Softmax 分类器进行分类输出。
3 实验与分析
3.1 数据描述与预处理
本文采用了由格拉茨科技大学知识发现研究所脑-机接口实验室提供的运动想象数据集[16],分别为四分类的BCICIV_2a 数据集与二分类的BCICIV_2b数据集。
BCICIV_2a 数据集是基于线索的无反馈四分类(左手、右手、双脚和舌头)数据集,该数据集采集了9 名受试者两天的脑电数据,其中包括22 通道的EEG 数据与3 通道的眼电数据,采样频率为250 Hz,每个通道都经过了0.5 Hz~100 Hz 的带通滤波器和50 Hz 的陷波滤波器进行预处理。9 名受试者分别经历了两天的采集实验,每天进行6 轮采集,每轮采集48 条脑电数据(其中,四类任务各12 条)。本文使用第一天采集的数据作为训练集,第二天采集的数据作为测试集。此外,本文采用相关研究中常见的[0,4]s 线索后时间窗切割数据集。综上,BCICIV_2a数据集包含9 个子数据集,每个数据集有288 条样本,其尺寸为(22×1000)。
本文所采用的第二个数据集为BCICIV_2b 数据集,该数据集是基于线索的二分类数据集(左右手),也来源于9 名不同的受试者。数据集的采集频率和滤波处理与BCICIV_2a 数据集一致。不同点在于BCICIV_2b 数据集只采集了6 个通道的数据(3 通道EEG 数据与3 通道眼电数据)并且进行了五天的采集。该数据集前两天采集的数据为无反馈的实验范式,后三天采集的数据为有反馈的实验范式。本文将前三天的数据集作为训练集,后两天的数据集作为测试集,其每个样本的尺寸为(3×1 000)。
目前大多数研究都对MI-EEG 数据集进行带通滤波处理,为了降低自适应滤波器组的学习难度、加快学习速度,本文对上述数据集进行了4 Hz~40 Hz的带通滤波并剔除人工标记的脏数据。此外,本文不对数据集做任何预处理,使用原始的数据进行学习,从而避免特征丢失。
3.2 实验设置
本文采用的学习批次大小为64,损失函数为分类交叉熵,采用Adam 算法作为优化算法,学习率设置为0.001,激活函数使用ELU 函数,模型层的参数初始化采用标准Glorot 方法,Dropout 参数本文设置为0.7,K1、K2设置为7 和9。由于两种数据集的通道数和任务难度不同,所以本文单独设置了网络模型中的F1和D参数,BCICIV_2a 数据集的F1、D设置为32、4;BCICIV_2b数据集的F1、D设置为16、2。实验的编程语言为Python3,深度学习框架为Tensorflow2.4,并且通过Nvidia GeForce RTX 3090 显卡进行训练。
本文将划分出来的训练集再划分为训练集(占原训练集的80%)和验证集(占原训练集的20%)。由于训练集的样本较少,充分利用验证集的训练策略更加适用于MI-EEG 数据集。因此,本文借鉴了计算机视觉领域开发的两阶段训练策略并加以调整[16]:①第一阶段,通过早期停止策略用训练集训练模型,并且监测验证集的精度。当验证集精度历经200 轮训练不增加时,就满足早期停止条件。此时,将模型的参数回滚到当验证集达到最佳精度时的模型参数;②第二阶段,加载第一阶段保存的模型参数,继续在验证集和训练集上训练,当验证集的损失值小于等于第一阶段训练集损失值时,停止训练并保存模型。
3.3 评价指标
为了评估提出方法的性能,本文采用两种最常见的指标进行性能评价,即精确度(Accuracy,Acc)和K系数(Kappa)。其公式分别为:
式中:TP、TN、FP 和FN 分别代表真正例、真反例、假正例和假反例,prand代表随机猜测的准确度。若不剔除脏数据,则四分类的prand=0.25。
3.4 单被试分类对比实验
3.4.1 BCICIV_2a 对比实验
为了证明所提方法的有效性和精确性,本文首先在BCICIV_2a 数据集上进行四分类任务的对比实验。本小节展示了所提方法与基于深度学习和传统机器学习方法的对比结果。其中,基于深度学习的方法包括DRDA[20]、M3DCNN[23]、DMTLBCI[24]、FBCNet[19]、TCNet[18]、C2CM[12]、EEGNet[17]和ShallowNet[16];基于传统机器学习的方法包括SSMM[20]和FBCSP[9]。对比结果如表2 所示(A1~A9 代表9名BCICIV_2a 受试者的编号,SD 为标准差)。
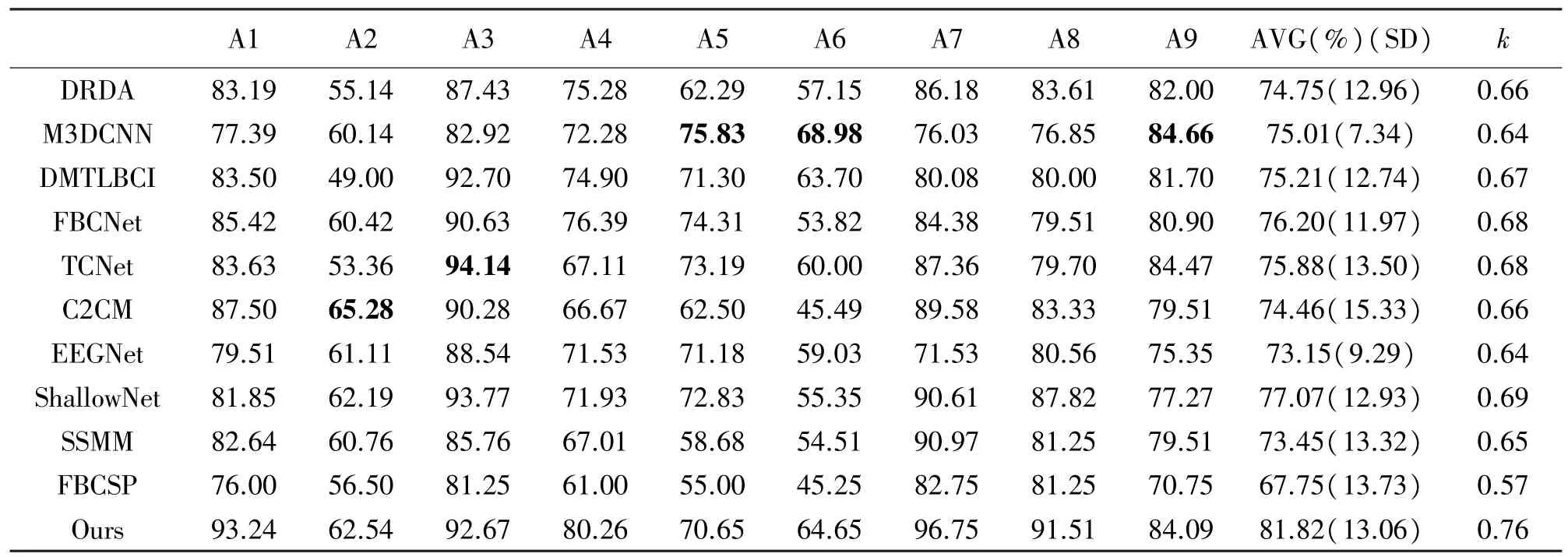
表2 BCICIV_2a 单被试对比实验数据:AFBCNet 与其他方法的对比。最佳的Acc 与K 用粗体标识
表2 列举了十种先进的MI-EEG 分类算法在BCICIV_2a 数据集上的个体准确率、平均准确率、标准差和K系数。本文提出的方法明显优于其他机器学习算法,对单被试的平均准确率达到了81.82%,K系数达到了0.76。图3(a)给出了测试集上的实验结果和混淆矩阵。FBCSP 是一种常见的EEG 机器学习基线方法,该方法通过频带划分与构造最优空间滤波器来提取特征,最后采用支持向量机进行分类。该方法在BCI 竞赛上获得了优胜,但是其平均准确率仅有67.75%,比本文所提出的方法低了14.07%。SSMM 作为SMM[20]的改进方法,使用稀疏支持矩阵机对复杂的矩阵式EEG 信号进行回归正则化,将数据转化到低秩来捕捉固有的结构特征,弥补了传统分类器的结构信息丢失问题,其准确率为73.45%。综上所述,本文提出的方法在多分类脑电信号数据集上的性能明显优于传统机器学习方法。
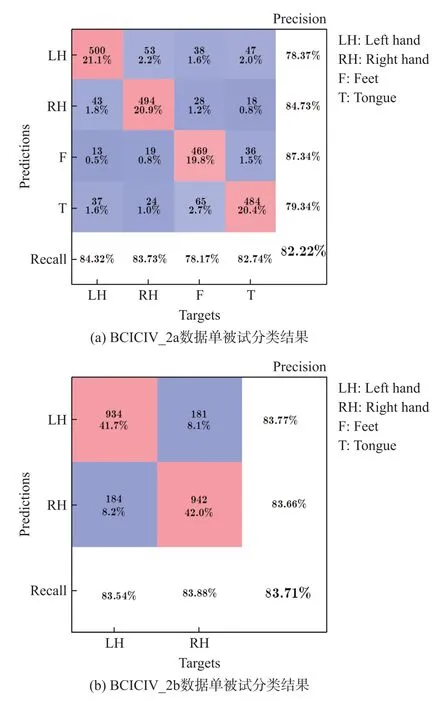
图3 MI 单被试分类实验结果的混淆矩阵
近年来,基于深度学习的方法已经在MI-EEG分类上领先了传统的机器学习方法,本文比较了近几年来最先进的深度学习方法,其平均准确率在73%到78%之间,略强于传统的机器学习方法。DRDA 和DMTLBCI 是基于迁移学习的方法,其准确率相比于传统机器学习方法有了明显的提升,分别达到74.75%和75.21%。DRDA 通过迁移多个受试者的EEG 数据来提高单被试的分类效果,该方法联合优化了特征提取模块、分类器和领域鉴别器。其中,领域鉴别器通过对抗学习的策略来匹配受试者之间的特征分布偏移,但是这类方法考虑了其他受试者的脑电数据,很难从中学习到有用的信息,且训练难度很大。FBCNet、TCNet、EEGNet 和ShallowNet是基于信号分解范式的卷积神经网络,精度分别达到76.2%、75.88%、73.15%和77.05%。此外,基于信号分解范式的卷积神经网络目前在精度上、计算量、内存需求和模型设计上都处于领先地位。因此,本文所提出的方法也继承了这类方法的优势,在精度上更是达到了81.82%。M3DCNN 使用复杂的三维EEG 数据表示与多分枝结构来改善模型性能,并证明了三维表达能够有效提高模型分类精度,但是其精度、计算开销上都远比本文所提出的方法要低。因此,挖掘二维数据的关联性和内在特征比使用复杂结构的数据更加有效。C2CM 利用混合通道卷积对时空特征进行分类,其精度达到74.46%。虽然C2CM 取得了不错的性能,但是这种方法微调了每个受试者的模型体系结构参数(卷积核大小和节点个数等),而本文提出的方法对所有的受试者都采用一致的结构与参数,这使得本文提出的模型能够快速地适应线下真实应用场景。此外,本文所提出的方法在6 名受试者的平均精度上达到了80%以上,且其中3 名受试者的准确度达到了90%以上,只有3 名受试者的分类精度在80%以下。在其他研究中,这三名受试者的分类精度也无法得到有效的提升,因此可以认为这类受试者是运动想象盲。
此外,表2 列举了各个方法的标准差,其中M3DCNN 的标准差最小,而本文所提出的方法的标准差为13.06,其中可能的原因是部分受试者的解码效果取得了非常高的精确度,而运动想象盲的精确度与其他受试者的精确度差距增大。除去三名被认为是运动想象盲的受试者,本文所提方法的标准差为6.24,并且平均精确度达到了89.75%,进一步证明了所提方法在善于运动想象的受试者中的稳健性与可靠性。
为了进一步证明AFBCNet 的解码和分类能力,本文对BCICIV_2a 数据集的A7 受试者进行t 分布随机领域嵌入(t-Distributed Stochastic Neighbor embedding,t-SNE)分析[8]。这是一种高维数据可视化的降维技术,结果如图4 所示。图4(a)是A7 受试者原始数据的降维投影,可以看到在未经解码时,其数据是混乱且不可分的。图4(b)是A7 受试者的经过AFBCNet 分解后的降维特征,除了小部分的重叠区域,四类任务都具有高度的聚类性和离散性。

图4 A7 受试者的t-SNE 分析
以上结果与分析表明,对于难度较大的四分类BCICIV_2a 数据集,AFBCNet 优于传统的机器学习方法(平均提高11.22%)和近年来先进的深度学习方法(平均提高6.6%),并且在单被试的分类实验中的表现最佳,比次优方法(ShallowNet)的精度高出4.75%。此外,本文所提出的方法在个体A1、A4、A7 和A8 上取得了最佳解码、分类效果。
3.4.2 BCICIV_2b 对比实验
为了进一步的验证本文提出方法能够胜任不同难度的任务,本文对二分类的BCICIV_2b 数据集进行进一步的单被试对比实验。本文不对网络结构做任何变动,仅调整F1、D和输出分类层的类别数。在BCICIV_2b 数据集上的单被试对比实验结果如表3 所示(B1~B9 代表9 名BCICIV_2b 受试者的编号),其对应的混淆矩阵如图3(b)所示。
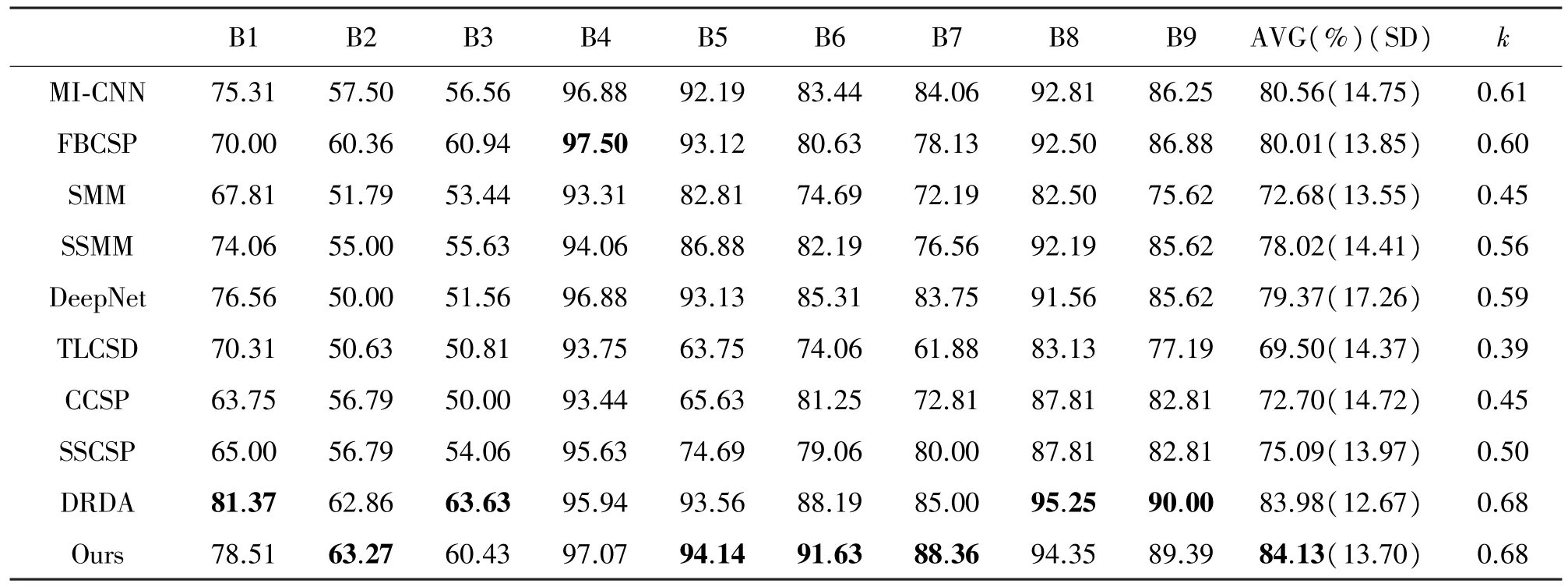
表3 BCICIV_2b 单被试对比实验数据:AFBCNet 与其他方法的对比。最佳的Acc 与K 用粗体标识
在较为简单的二分类数据集上,传统的机器学习方法也表现出了出色的性能。其中,FBCSP、SMM和SSMM 分别达到了80.01%、72.68%和78.02%的准确率。虽然FBCSP 在四分类的数据集上的效果远不如SMM(平均准确度70.75%)和SSMM,但是SMM 和SSMM 在二分类的数据集上表现却较差。这表明传统的手工提取特征方法和机器学习方法的泛化能力有限,而本文所提出的方法在仅调整F1和D参数的条件下,都能取得最优的平均性能。CCSP、SSCSP 和TLCSD 是基于自适应学习的机器学习方法[10],DRDA 是领域自适应的深度学习方法。CCSP 和SSCSP 的分类性能较差,这可能是由于这类方法假设不同受试者的空间滤波器是相近的,并且通过逼近协方差均值的方式来估计协方差矩阵,然而事实上,不同的受试者之间的数据隔离性较大。DRDA 在二分类的数据集上的表现接近本文所提出的方法,但是其在四分类的数据集上的效果比AFBCNet 低了7.07%,且训练过程复杂,这说明领域迁移学习虽然有效,但是对于复杂的任务很难学习到有用的跨被试信息。
以上结果表明,本文提出的方法不仅在高难度的四分类数据集上有显著的提升,在二分类的数据集上也同样表现不俗,略高于次优的DRDA算法。因此,对于不同的数据集和不同难度的任务,本文提出的网络模型具有很强的自适应性与鲁棒性。
3.5 跨被试分类对比实验
目前,大多数研究都集中于单被试的实验与模型训练,上述的实验就是基于这种范式开展的,并且证明了本文提出的方法在这种情况下表现最佳。此外,为了验证模型的健壮性与迁移能力,本文展开了第二种基于迁移学习范式的实验,并在BCICIV_2a数据集上与DeepNet[16]、ShallowNet、DMTLBCI 和PSTSANN[25]算法进行比较。第二种实验范式首先使用其他被试(不包括目标受试者)的EEG 数据进行预训练并保存参数,然后使用目标受试者的数据继续进行第一种实验范式的训练并进行测试。其结果如表4 所示。

表4 BCICIV_2a 跨被试迁移学习分类实验结果。最佳的Acc 用粗体标识。
由于不同受试者之间的MI-EEG 数据差异较大,因此,跨被试实验的结果并不优于单被试实验的结果。在平均准确度上,本文所提出的方法相比于其他深度学习算法依然保持了最佳的性能,以1.96%的优势高于次优的PSTSANN,并且在A1、A2、A4、和A7 受试者上的表现最佳。此外,实验分类精度的大幅度退化主要发生在少数运动想象盲受试者上(A5 和A6),而在大多数受试者上精度退化在较小范围内。实验结果表明,本文提出的方法不仅在单被试的情况下表现最佳,而且具有较强的迁移能力与鲁棒性。
3.6 消融实验
为了研究AFB 和改进的Inception 层对模型的影响,本文删除一层来测试另一层的作用,结果如表5所示。由于模型紧凑且属于承前启后的分解范式,对于模型中层数的变动会极大地影响模型的精度。因此,只有Inception 或者AFB 层都不能对MIEEG 信号进行深度的解码与分类。从实验结果上来看,Inception 对于AFBCNet 的影响更大一些。

表5 基于BCICIV_2a 的模型消融实验
为了更加合理地证明AFB 和改进的Inception的作用,本文使用传统的卷积层来代替模型中的AFB 层(表5 中的CNN-Inception)进行实验,其精度达到76.76%,略高于基于时空分解范式的卷积神经网络(FBCNet、EEGNet 和TCNet),而与次优的ShallowNet 的表现非常接近。这表明通过改进的Inception 结构提取时空分解后的特征比采用方差层和时域卷积网络的效果更好。此外,相较于传统的卷积核,AFB 的引入在性能上提高了5.06%,且降低了学习难度、大幅度减小了计算量、增强了模型的可解释性。
4 结束语
本文提出了一种基于自适应滤波器组的运动想象卷积神经网络,在继承传统的解码型结构网络的基础上,更加注重解码的精度与可解释性。该模型在训练数量有限的多分类任务中能快速学习MIEEG 数据的内在特征并进行有效分类。在BCICIV_2a 和BCICIV_2b 数据集上的实验结果表明,本文提出的模型与传统的机器学习方法和近年来先进的深度学习方法相比有明显的优势。未来,我们计划进行线下采集实验与实际应用的研究。
