进给系统机电耦合仿真建模与误差影响规律分析
2024-01-09李海洲谢丽军周梦洁柏明剑朱润平
李海洲,谢丽军,周梦洁,柏明剑,朱润平,庞 伟
(1.东莞稳控自动化技术有限公司,广东东莞 523000;2.中国航空工业集团成都飞机设计研究所,成都 610041;3.东莞理工学院,广东东莞 523808;4.东莞市东莞理工科技创新研究院,广东东莞 523808)
0 引言
当前,我国现代机械制造业正朝着高精度、高速度、高效率的方向发展[1]。数控机床作为工业母机,其加工精度决定着工业制造水平的高低[2]。进给系统是数控机床的关键部件,该部件的性能对数控机床的精度影响很大[3]。因此,分析机床进给系统的稳定性,对于提高机床的加工速度和加工精度具有非常重要的意义[4]。
进给系统的动态响应特性受可动结合面、结构刚性变形、控制系统的响应性能等多因素影响,以上影响因素具有强耦合特点[5],这对动态响应特性的精确建模提出了巨大的挑战。
进给系统动态响应特性仿真分析研究方法主要有基于机电联合仿真建模与基于数学模型和Simulink 的建模方法。多位研究者用机电联合仿真的建模方法[6-9]考虑了进给系统实际运行时的接触变形、结合面刚度、阻尼、固有频率等。孙名佳、方晨曦、罗茹楠等[10–21]考虑了延时、摩擦等影响因素,用Simulink 进行仿真建模,分析其动态响应过程中的固有频率、跟随误差等影响。
本文从理论建模与基于Simulink 仿真两方面出发,对滚珠丝杠进给驱动系统的控制系统与机械传动系统进行数学简化,建立了进给系统的Simulink 仿真模型。搭建了单轴伺服进给系统实验平台,并通过理论推导、仿真分析与实验验证研究了位置环增益、位置、速度、加速度、间隙等因素对跟随误差的影响规律。
1 机电系统理论建模
1.1 进给系统动力学建模
本文采用交流永磁同步电机驱动的滚珠丝杠进给系统,其机械部分组成如图1所示。
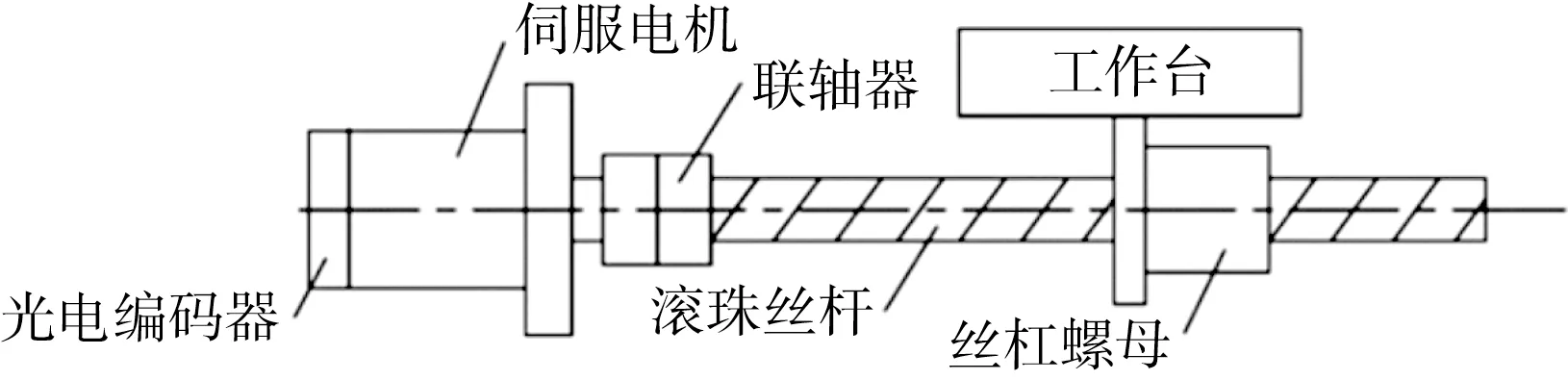
图1 进给系统的组成
伺服驱动器驱动电机旋转,电机轴通过联轴器带动丝杠旋转,进而转化为工作台的直线运动。进给系统的转矩平衡方程为:
式中:Tl为电机轴输出转矩;Ta为系统总惯性力矩;Tf为系统总摩擦力矩,包括支撑轴承的滚动摩擦、工作台承载滑块与导轨间摩擦、丝杠螺母副的摩擦力等;Tc为切削负载等效切削力矩。
进给系统总惯性力矩为:
式中:ωm为丝杠转速;J为系统总的转动惯量,包括丝杠、联轴器、轴承等旋转部件的转动惯量以及工作台、滑块等直线运动部件的等效转动惯量。
进给系统的摩擦力建模常见的有Stribeck模型[22]:
式中:Tfc为库伦摩擦力矩;Tfs为最大静摩擦力矩;vs为临界速度;σ 为黏滞摩擦因数,v为接触面的相对运动速度。
Stribeck 摩擦模型如图2所示。由Stribeck 摩擦模型可知,高速时摩擦力与速度基本是线性关系,但在启、停、过象限点等低速运动时,摩擦力与速存在很强的非线性,这对系统在低速阶段的运动跟踪精度产生不利影响。

图2 stribeck摩擦模型
此外,进给系统传动过程中,还存在如图3 所示的各种典型非线性影响因素。
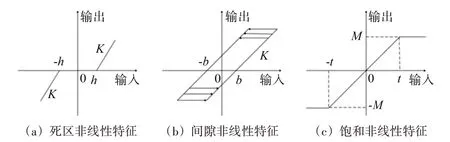
图3 进给系统典型非线性影响因素
因零部件本身尺寸精度、导轨的非线性摩擦,以及反向间隙、装配精度等因素影响,工作台的运动速度是变化波动的,与指令值存在一定偏差,这种偏差经伺服反馈调节引起伺服电机电枢电流变化,进而改变电机输出扭矩。图4 所示为电机轴由匀加速到匀速阶段的输出扭矩信号和速度信号。
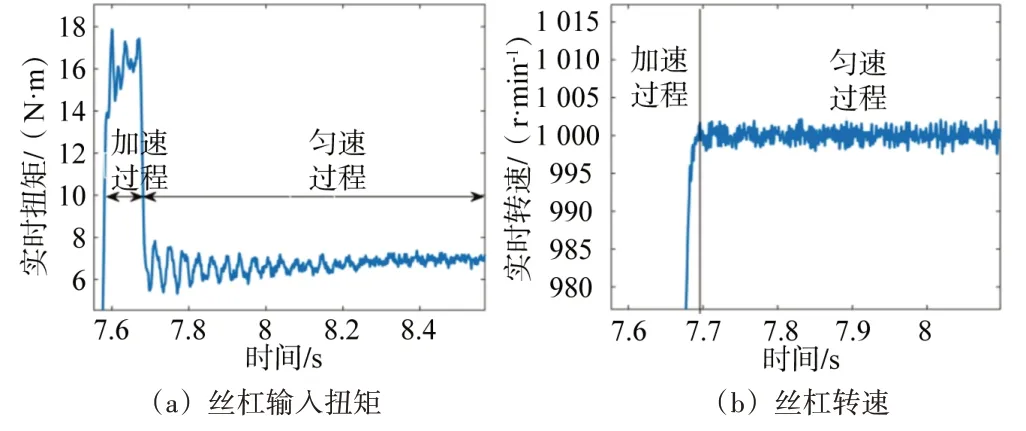
图4 进给系统丝杠输入扭矩与转速
可以看到,在匀加速阶段存在惯性力矩,加速和匀速段均存在明显的扭矩波动,电机轴的实际速度也并不稳定,说明进给系统在运动过程存在加大的非线性干扰,这种干扰将对进给系统的跟踪精度产生一定影响。
1.2 进给驱动系统控制模型建立
进给轴控制系统通常采用串联式闭环的三环控制结构,如图5所示。

图5 进给系统三环控制结构
(1)电流环:与交流永磁同步电机直接相连,实时监测电机的驱动电流大小,限制电机电枢的电流范围,提供有稳定的加速转矩。其响应速度快,能有效抑制内部干扰,在工程上常采用负反馈PI控制。
(2)速度环:位于中间的是速度环,利用丝杠末端编码器监测丝杠轴实时转速,与指令速度比较对电机转速进行调整,将整个电流环作为被控对象,抑制负载变化和外部干扰引起的速度波动,常采用负反馈PI控制。
(3)位置环:最外环是位置环,利用编码器或光栅尺监测的工作台实际位置,与指令位置进行比较,对工作台的位置进行调整,保证系统的位置跟踪精度和定位精度。根据三环控制系统的设计结构可知,相对于电流环和速度环,位置环的截止频率更小,这严重影响了位置控制器的快速性。因此,常采用P 控制来提高位置环响应的快速性。
基于以上三环结构,建立如图6 所示的单轴伺服进给系统的控制结构。

图6 单轴伺服进给系统PID控制结构
2 跟随误差影响因素理论分析
2.1 稳态误差分析
根据系统开环传递函数中积分环节的个数将系统分为0 型系统、Ⅰ型系统、Ⅱ型系统等,将上节伺服控制系统模型进行简化,以开环传递函数表示进给系统PID三环控制模型,则其误差传递函数如下:
式中:E(s)为系统响应误差;R(s)为指令输入。
根据终值定理可知,若系统稳定,系统稳态误差可由下式计算:
进给系统动态响应误差与进给轴速度、加速度等密切相关,实际加工作程中系统给定的运动指令常由多种典型信号线性组合而成,因此,本文以3 种典型信号作用下对系统的稳态误差进行分析:阶跃信号为r(t)=1(t),R(s)=1/s;斜坡信号为r(t)=t∙1(t),R(s)=1/s2;加速度信号为r(t)=t2/2∙1(t),R(s)=1/s3。将上述3 种典型信号的R(s)代入,可以计算得到该信号输入下的系统稳态误差:
式中:C0为位置误差系数;C1为速度误差系数;C2为加速度误差系数。
可知,当进给系统的控制参数确定时,其响应的跟随误差仅由输入决定。进给系统的指令输入信号主要是由上述3 种典型信号线性组合而成,因此,其跟随误差也是输入指令中位置、速度、加速度分量的组合。
2.2 跟随误差的计算
对于PID 三环控制这样的线性系统,其脉冲输入响应的拉式变换等于其传递函数。线性系统的输入输出满足卷积关系:
式中:u(t)为系统输入;h(t)为脉冲响应;x(t)为系统输出。
根据此关系计算任意输入下系统的响应输出:
式中:w(k)为单位脉冲响应。
根据脉冲响应的特性,脉冲响应在时域上具有一定宽度N,当k<0 及当k>N时,w(k)=0,因此,系统输出可以表示为:
可以看到,通过数值法计算脉冲响应的有限项,可以得到对应的输出。但这种方法需要事先知道系统的脉冲响应函数,且需要大量繁琐的求和计算,过程复杂。考虑PID 三环控制模式下的进给控制系统可以看做是一个二阶系统,其跟随误差可近似如下:
可知,跟随误差与位置、速度、加速度存在相关性,是跟随误差的重要影响因素。
3 基于Simulink的进给系统动力学仿真分析
3.1 进给系统动力学模型参数的设置
(1)机械结构参数
本文利用KISTLER 扭矩传感器采集的电机输出扭矩信号,对进给系统的总等效转动惯量和阻尼进行辨识,得到简化后进给系统的等效转动惯量和阻尼如表1所示。

表1 进给系统机械结构参数表
(2)交流永磁同步电机参数
在本文所搭建的单轴伺服进给实验台中,选用的是YASKAWA 公司生产的Σ-7 系列SGM7G 型交流永磁同步电机。根据Σ-7系列电机选型手册中所给参数进行计算,可以得到相关的仿真参数,如表2所示。

表2 进给系统伺服电机参数表
(3)PID三环控制参数
进给伺服系统采用的是PID 三环控制结构,经整定过后,可以得到如表3所示的进给系统仿真控制参数。

表3 进给系统PID三环控制参数表
根据上述参数,建立了进给系统的Simulink 仿真模型,如图7所示。

图7 进给系统Simulink仿真模型
3.2 伺服控制参数与丝杠间隙对动态响应误差的影响
(1)位置环增益对跟随误差的影响
以2.2节建立的进给系统动力学模型为基础,保持模型其他参数不变,改变系统位置环增益,分别取Kp为100、150、200、250、300、350、400 时,进给系统对阶跃信号输入、斜坡信号输入以及正弦信号输入的动态响应,其仿真结果如图8所示。
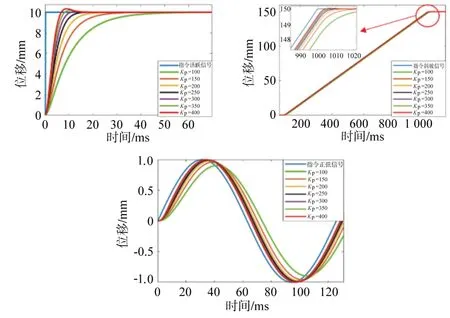
图8 不同位置环增益下的系统响应
由图8(a)可知,位置环增益Kp在由100 逐渐增加到400 的过程中,进给系统对阶跃信号的响应逐渐产生超调量,响应速度越来越快;由图8(b)可知,随着进给系统位置环增益Kp的增大,进给系统匀速运动的跟随误差逐渐减小,但减小的幅度在逐渐降低,同时达到稳态的时间也逐渐减小,当Kp达到200 后跟随误差大小基本不再变化,只是稍微有点下降;由图8(c)可知,对于速度时变的正弦信号,在反向点处,由于实际位置响应滞后于指令,导致进给系统在运动指令反向后一段时间参才反向,这将导致实际加工过程中产生相应的轮廓误差,但这种误差随着Kp的增大逐渐减小,并在Kp达到200后基本趋于稳定。
综上所述,进给系统位置环增益Kp对载荷突变过程、匀速运动过程以及周期性变速运动过程的跟随误差均会产生显著影响。
(2)丝杠间隙对跟随误差的影响
以建立的进给系统动力学模型为基础,改变进给系统的进给加速度的大小,分别取丝杠间隙Cn为0.00、0.01、0.02、0.03、0.04、0.05 mm 时,仿真进给系统对正弦信号输入的动态响应,保持匀加速运动至速度达到1 200 mm/min。其仿真结果如图9所示。
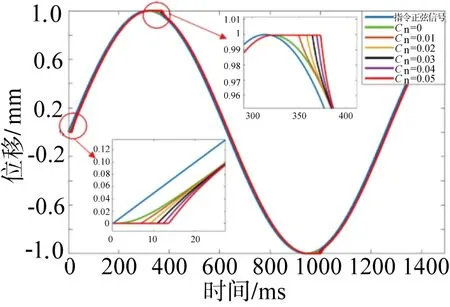
图9 不同间隙下进给系统的动态响应
与无间隙相比,当丝杠间隙存在时,进给系统在启、停点处以及速度反向点处的动态跟踪精度会迅速下降,工作台在经过这些启、停、反向点处时,跟随误差会迅速累积丝杠间隙而发生突然增大,而与进给系统的控制参数无关。在工作台走过间隙区间后,此时很大的跟随误差值将被PID三环控制系统逐渐补偿,有、无间隙的位移输出响应曲线慢慢重合,但这个过程将消耗一段时间,表现为相对于无间隙的进给系统,有间隙的进给系统在反向点前后的一个时间区段内跟随误差会突变,这个区间段的长度与间隙大小呈正相关,有、无间隙的跟随误差差值会先增大后减小的,且这种差值的变化是非线性的。
4 跟随误差影响因素相关性验证
4.1 实验平台搭建
本文搭建了单轴伺服进给系统实验平台,如图10所示。

图10 单轴伺服进给系统实验台
4.2 误差影响因素相关性验证
(1)位置的相关性验证
如图11 所示,通过输入指令的整体平移使运动轨迹在进给台上的位置发生改变,以此进行位置相关性验证。
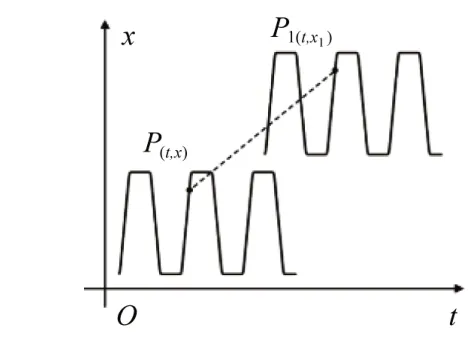
图11 单轴伺服进给系统直线轨迹
同一轨迹在不同位置下的响应特性误差对比如图12所示。由图可知,在第二个位置下的跟随误差与第一个位置下的跟随误差之差在±0.003 mm范围内波动,而此实验平台的的重复度误差也在0.004 mm 左右,其跟随误差的大小和变化趋势并不会改变,即跟随误差与位置并不相关。
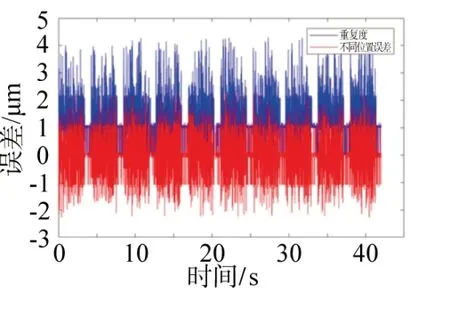
图12 不同位置下的跟随误差对比
(2)速度的相关性验证
以梯形加减速的直线运动轨迹来进行速度相关性实验,分别进行进给速度为4 000、6 000 mm/min 两组不同速度下的直线轨迹运动,比较不同速度下跟随误差的大小和变化趋势。不同速度下的跟随误差按轨迹展开后的曲线如图13所示。
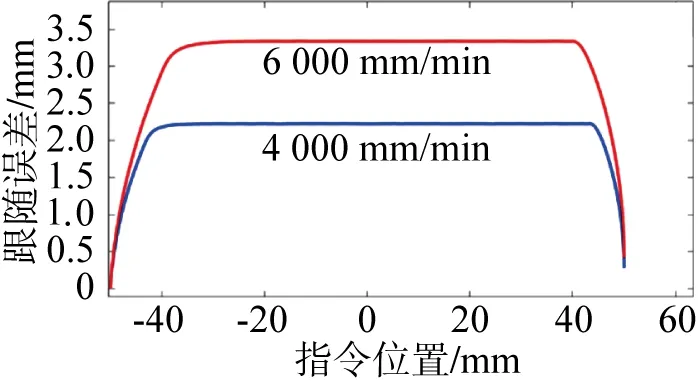
图13 不同速度下的跟随误差对比
可以看到,进给速度由4 000 mm/min 变化到6 000 mm/min的后,跟随误差的变化趋势基本一致,但跟随误差的大小明显不同。在4 000 mm/min 时,匀速段的跟随误差稳态值在2.2 mm 左右,而当进给速度变为6 000 mm/min 时,匀速段的跟随误差稳态值增大到了3.4 mm左右。而且可以发现,随着速度的增大,跟随误差也相应增大。由此,跟随误差和进给速度有较强关联性。
(3)加速度的相关性验证
以重复的梯形加减速运动轨迹来进行跟随误差加速度相关性实验,分别进行加减速时间常数为200、300 ms 时的轨迹运动,所对应加减速段的加速度分别为500 mm/s2和333 mm/s2。去除速度相关部分跟随误差后的跟随误差曲线如图14所示。

图14 不同加速度下的跟随误差对比
可以看到,当加速度由333 mm/s2变化到500 mm/s2后,跟随误差的变化趋势保持一致,但跟随误差的大小发生了显著变化。加速度为333 mm/s2时,加速度段跟随误差最大值约为0.29 mm,当加速度增加至333 mm/s2后,加速度段跟随误差最大值增加到了约0.42 mm。由此,跟随误差和进给加速度具有一定的相关性。
综上所述,速度、加速度是跟随误差的重要影响因素,而位置基本对跟随误差无影响。
5 结束语
本文对滚珠丝杠伺服进给系统进行简化,利用Simulink 仿真工具建立进给系统的动力学仿真模型,从理论上分析了系统动态响应过程中的稳态误差,利用仿真模型分析了位置环增益以及速度、加速度、间隙等对跟随误差的影响。同时,在单轴伺服进给系统实验台上进行了跟随误差影响因素的相关性验证,明确了速度、加速度与跟随误差的相关性,为进给系统非稳态跟随误差的精确建模和预测奠定了基础。
