物流装卸机器人运动学分析及碰撞检测研究*

魏 鹏

（泉州华中科技大学智能制造研究院，福建泉州 362000）

0 引言

物流系统是生产系统中至关重要的组成部分。为了提高物流效率、减轻工人的劳动强度以及便于管理，物流机器人在物流行业得到了广泛应用。这些物流机器人包括AGV 小车、码垛机器人、分拣机器人等，它们被用于实现搬运、装卸、分拣等任务的自动化[1-5]。但是，当面对从集装箱中装卸箱包这种任务时，常见的六轴机器人、SCARA 机器人和Delta 机器人会存在刚性不足、效率不高和经济性差等问题。基于此，本文设计一种适用于从集装箱内装卸箱包的物流装卸机器人。

物流装卸机器人被部署在货物装卸区域，其主要任务是将货物从地面装入集装箱或将货物从集装箱内搬出。这个工作场景通常发生在物流中心、港口、货运站等地方，其中集装箱是一种常见的货物运输容器。当货车司机驾驶集装箱货车将车辆调整到适当的角度和位置后，车辆往往不再频繁移动，而是停留在指定的装卸位置上。因此，集装箱的相对位置相对固定，物流装卸机器人可以利用视觉或雷达设备获取集装箱的位姿信息，以便进行后续的操作和碰撞检测。

近年来，也有许多企业工程师和学者对物流装卸机器人进行研究。顾绮芳[6]针对货柜车厢的作业环境，设计空间七连杆机构、二转动自由度差动机构实现机械臂在行程范围内能达到货箱中任意位置，并通过空间轨迹视觉引导实现快速精确移动定位。韩祥东[7]以井下矿用坑道钻机的钻杆装卸为应用背景，进行运动学动力学建模，使用人工蜂群算法进行最优冲击轨迹优化，并设计了装卸机器人的控制系统以及操作界面。

本文主要完成物流装卸机器人的运动学建模、逆解公式推导、仿真验证、可达空间分析和碰撞检测研究。

1 物流装卸机器人结构介绍

物流装卸机器人结构如图1 所示。机器人整体可分为两大部分，一部分是可移动底座，另一部分是由旋转平台、旋转臂、支撑臂等零部件组成的五轴机械臂，当横向旋转臂移动到集装箱内指定位姿后，可将货物经由旋转臂上的传送带运送至集装箱内。

图1 物流装卸机器人结构简图

五轴机械臂部分是一种五关节的串联机构，5 个关节均为转动副，J1轴的旋转运动可实现旋转平台与可移动底座之间绕Z轴的旋转；J2、J3和J4轴的旋转运动可实现相邻连杆之间绕X轴的旋转；J5轴的旋转运动可实现横向旋转臂与纵向旋转臂3 之间绕Z轴的旋转。其中J1、J4和J5由电机直接驱动，J2、J3由支撑臂间接驱动，支撑臂上安装有伺服液压缸，可以提供更好的支撑和稳定性。θi为连杆i的转角，Li为连杆i的长度，S1、S2、S3和S4为支撑臂在底座和连杆上的安装尺寸。

2 机械臂运动学建模与求逆

2.1 运动学建模

如图2 所示，基于物流装卸机器人的机械臂三维结构建立其连杆坐标系，分别命名为机器人基坐标系{B}、第一关节轴静坐标系{Js1}、第一关节轴动坐标系{Jd1}、第二关节轴静坐标系{Js2}、第二关节轴动坐标系{Jd2}、第三关节轴静坐标系{Js3}、第三关节轴动坐标系{Jd3}、第四关节轴静坐标系{Js4}、第四关节轴动坐标系{Jd4}、第五关节轴静坐标系{Js5}、第五关节轴动坐标系{Jd5}。

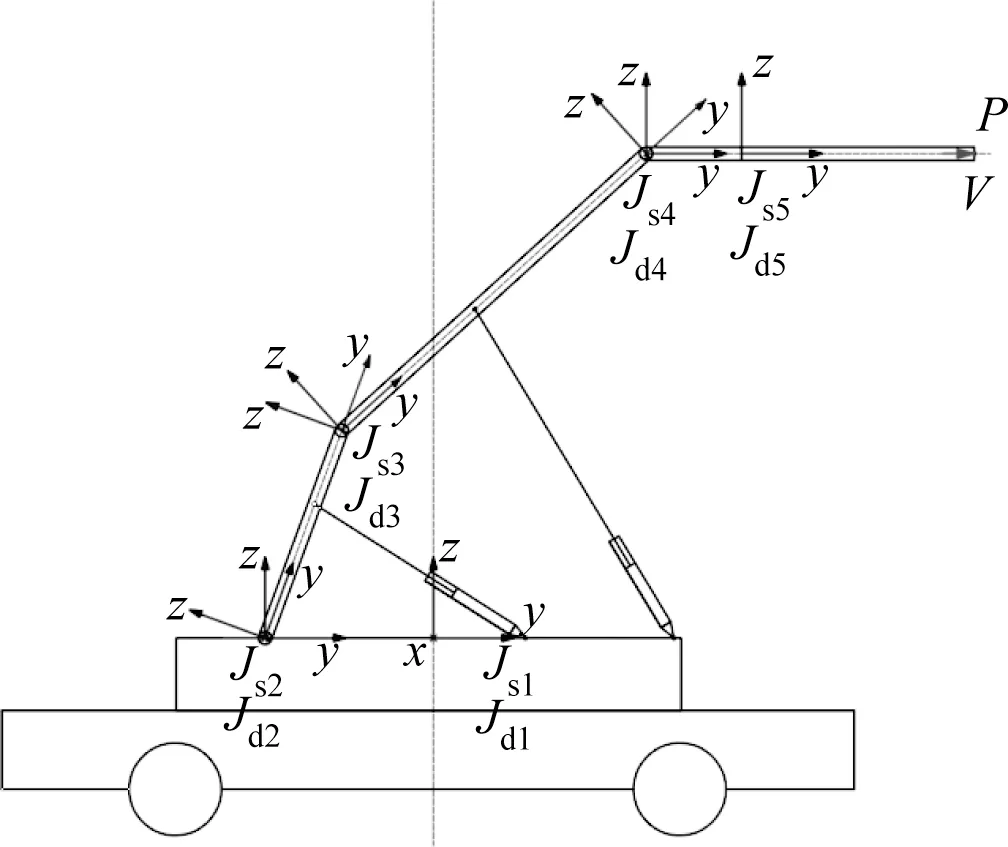
图2 各轴坐标系示意

建立各坐标系之间的转换矩阵。T表示转换矩阵，具体为从左上标坐标系到左下标坐标系的转换矩阵。依次建立。由于{B}的原点位置可以任意选取，令{B}与{Js1}重合，则为单位矩阵。设矩阵运算符号如下：

由式（1）便可以实现正向运动学求解。

2.2 求运动学逆解

常见的逆运动学求解方法有几何法、解析法、数值法，近年来随着人工智能热潮，一些人工智能的方法也得到了应用[8]。国内外学者对机器人逆运动学方法进行了深入的研究。马建伟等[9]针对六自由度串联机械臂，在Levenberg-Marquardt（LM）迭代法求值的基础上，针对迭代参数因子和步长，提出改进的逆运动学问题数值解法。刘曰涛等[10]针对KUKA 机器人，使用反变换法计算机器人逆运动学解，并通过算法筛选和条件限制确定唯一解。刘国平等[11]针对一种前3 关节轴线交于一点的六自由度机械臂，提出一种旋量理论结合已知pandenkahan 子问题的逆解方法，将旋量、几何法、欧拉角相结合，简化了传统旋量求解方法。

该机器人共有5 个关节轴，没有冗余的关节，所以可以求出解析解。本文采用几何推导的方式求出其解析解。在求逆的过程中，默认控制点BP=[x y z1]T和控制方向BV=[i j k0]T已知，且连杆的长度尺寸Li已知。

2.2.1 求θ1、θ2、θ3、θ4、θ5

（1）对 控制 向量BV=[i j k0]T进行单位化处理，使得其向量长度为1。单位化公式为：

用BVnorm=[inormjnormknorm0]T表示单位化后的控制向量BV。

（3）分析机械臂在oxy平面内的投影关系可知，θ1由xJd5与yJd5决定，θ1的求解公式如下：

（4）纵向旋转臂1、纵向旋转臂2 与纵向旋转臂3 共同构建了一个平面，将其命名为纵向旋转面，

求出该平面在{B}坐标系下的单位法向量BVver-lon-plane的表达式：

（5）θ5是控制向量BV=[i j k0]T与纵向旋转面之间的夹角，纵向旋转面的法向量BVver-lon-plane已知，公式如下：

θ5的求解还需要进行符号判断，当BV的x方向分量大于BVver-lon-plane的x方向分量时，θ5的符号为负，反之为正。

（6）求出控制方向BV=[i j k0]T在纵向旋转面内的投影向量BVp-lon-plane，公式如下：

（9）在第二关节轴静坐标系{Js2}内，求解θ2、θ3、θ4。在{Js2}内，纵向旋转臂1、纵向旋转臂2 与纵向旋转臂3 构成了一个典型的SCARA 机器人结构，相关的研究非常丰富，本文不再重复推导，直接列出如下公式：

2.2.2 求解D1、D2

利用三角函数关系，把θ2、θ3转换成D1、D2。角度与长度转换关系如图3 所示。旋转角θ1、θ4、θ5可由安装在关节上的电机旋转实现角度调整，而θ2、θ3所处的位置等效转动惯量较大，若直接用电机在关节上进行驱动，稳定性难以保证，所以采用伺服液压缸间接控制θ2、θ3。转换公式如式（11）所示。

图3 角度与长度转换关系

3 仿真验证与可达空间分析

3.1 数值仿真

使用MATLAB 对机器人逆运动学准确性进行验证。给定机械臂长度，L1～L5分别为400、850、5 104、175、1 660 mm。选取机器人末端起始点位置[-300 7 000 200]，方向向量[0 1-0.5]，终止点位置[300 7 000 200]，方向向量[0 1-0.5]，取插补数ns=100，分别对末端位置和方向进行平均插补，得到期望轨迹上各插补点位置[pex pey pez]与归一化方向向量[vex vey vez]。根据本文所提出的逆运动学解法得到各关节转角，再进行正运动学求解获取各插补点实际位置[prx pry prz]与归一化方向向量[vrx vry vrz]。末端执行器轨迹如图4所示。

图4 末端执行器轨迹

计算期望轨迹与实际轨迹在各插补点的位置误差Δp与方向误差Δv，其中：

由数值计算结果可知，在该轨迹中位置误差最大值Δpmax=2.365 5×10-10，方向误差最大值Δvmax=1.425 0×10-13。算法引起的误差在数值上很小，使用该运动学逆解方法可实现末端轨迹的准确规划。

3.2 可达工作空间分析

机器人可达空间的求解方法主要有几何法、解析法以及数值法三类[12]。几何法利用几何绘图的原理确定工作空间的边界，从而表示机器人工作空间。解析法主要通过求解工作空间边界的包络问题，得到边界方程，从而进行工作分析。于英红等[13]从构成并联机构的基本单元出发，研究了其位置正解与反解的分析方法，以3-RPS并联机构进行分析，得到其工作空间分析的解析方法。而数值法计算机器人工作空间时，通过运动学正解得到一系列末端位置，从而得到工作空间的边界曲面与曲线。数值法中应用较为广泛的是蒙特卡洛法，蒙特卡罗法是一种以概率统计为指导的数值计算方法，通过大量的正解模拟出机器人的工作空间。杨永鲲等[14]为进行焊接机器人工作空间分析，使用蒙特卡洛法，在关节限位内对关节变量进行随机赋值，获取焊接末端点。许如宾等[15]在电子设备电磁兼容检测近场成像的六轴机械臂应用中，给定末端天线姿态，使用蒙特卡洛法求解其末端执行器工作空间，并证明该空间内存在一个不可达球域。

根据该机器人尺寸参数，并考虑机器人关节以和液压缸的实际约束条件，在MATLAB中进行机器人正运动学求解，取计算点数nc=10 000进行遍历，得到机器人工作空间云图，将其沿各坐标轴进行二维投影，结果如图5所示。

图5 工作空间仿真

总体上，可达工作空间在Z方向两端收缩，如图5（a）所示。在图5（b）中，由于机器人关节1 和5 旋转角的限制，且机器人旋转臂1、2、3 始终构成一纵向平面，使xoy平面投影的扇形图像限定在一定角度范围内。当机器人末端趋于可达工作空间两端时，横向旋转臂转角θ5趋于0，使末端的x方向可移动距离减小，但由于末端绕z轴转动由θ1和θ5共同作用，且θ1的改变不影响末端z坐标值大小，因此在工作空间z方向两端θ1可取范围内的任意值，使得扇形图像的下端收缩并保持一定转角，从而产生图5（b）。当机器人末端远离可达空间两端时，θ5的取值范围放宽，使机器人在x方向的可移动距离变大，所以产生了如图5（c）所示的鼓形图像。

4 碰撞检测研究

由于该物流机器人需要在货物大小不一、空间有限的货箱中完成装卸任务，对机器人进行碰撞检测，合理规划其运动轨迹是有必要的，以避免造成对货物、货箱乃至机器人本体的破坏。

目前，已有众多学者进行了机器人碰撞检测方向的研究，主要的实现方法有基于几何建模方法、基于外部传感器和视觉的方法、数字孪生方法等[16-18]。朱战霞等[19]针对障碍环境中自由漂浮模式空间冗余机械臂进行了球形包围盒和空间叠加思想研究，简化描述障碍物和空间机械臂的占位关系，使用直线段和球体判断碰撞。王张飞等[20]提出了一种基于深度投影的点云目标实时分割方法，并使用该分割后的点云目标构造混合层次包围盒进行碰撞检测。江雪梅等[21]将数字孪生引入重型机床碰撞检测，构建了感知-演化预测-反馈的碰撞检测框架，动态感知工件刀具等加工要素，对潜在的干涉现象进行预测。

对于机器人的碰撞检测，本文采用圆柱包络法。由于旋转平台、纵向旋转臂1 和支撑臂都位于靠近移动平台的位置，并且在各自的可达范围内都不会发生碰撞，因此只需要对纵向旋转臂2、纵向旋转臂3和横向旋转臂进行包络处理。包络线如图6所示。

图6 包络线示意

考虑到集装箱的厚度较小且几何形状接近长方体的外表面，使用线段集对集装箱进行碰撞检测建模。具体方法如下：将集装箱长方体的4 个棱进行数学表达，并选择与棱平行的其他线段作为参考线段。确保各线段之间的间距不大于L，其中L是纵向旋转臂2、纵向旋转臂3 和横向旋转臂所形成的包络圆柱体的最小半径。

包络完成后，逐个求解圆柱中心线线段和箱体线段之间的距离，判断该距离是否小于圆柱半径即可，若小于，则发生碰撞，若不小于，则不发生碰撞。通过这种方法，可以有效地检测机器人在操作过程中与集装箱之间的碰撞情况，并采取相应的措施以确保安全运行。

5 结束语

本文基于物流装卸机器人的结构，建立了机器人的运动学模型，推导了机器人的逆运动学求解方法。该方法简洁可靠，并具有快速求解的特点，适用于实时控制系统。通过计算机仿真，验证了逆运动学的有效性，并用数值方法求解了机器人的可达空间。所得结果为机器人的结构改进提供了重要的参考，可以用于优化机器人的尺寸参数。同时，研究了机器人的防碰撞问题。针对机器人与障碍物之间的碰撞风险，进行了包络建模研究。

下一步可在本文研究的基础上，以视觉拍摄结果为输入，结合碰撞检测结果规划末端执行器的运动路径，使其能够高效且安全地完成装卸任务。