基于改进多目标粒子群优化算法的列车节能研究*

□ 金瑷瑶 □ 李文强 □ 武瑞杰 □ 顾富国 □ 毛绅宇 □ 朱 楠

江苏理工学院 汽车与交通工程学院 江苏常州 213001

1 研究背景

近年来,我国城市轨道交通实现飞速发展。随着运营规模的扩大,城轨交通系统总电耗不断攀升,其中,牵引能耗占总电耗的比例达49.8%,因此必须采取节能运行策略来降低牵引能耗。列车牵引能耗受线路设计影响,与列车驾驶模式有关。陈明亮等[1]分析单面坡与多段坡内列车能耗,得出经济适用的节能坡设置参数。在列车驾驶模式方面,曹佳峰[2]研究牵引惰行交替节能模式和四段模式在五种不同坡道的能耗表现。在列车运行速度曲线求解算法方面,已有文献多采用启发式算法,如文献[3-5]采用改进遗传算法来获得列车的运行速度曲线。但是,遗传算法的生物遗传概念与列车工况转换点需要通过二进制对应,而且难以避免交叉、变异、选择等复杂操作。杨志清等[6]采用改进自适应粒子群算法获得列车最优控制方案,但仿真环境中坡度过于单一。鲍鹏宇等[7]采用粒子群算法求解列车分段曲线制动点,但粒子群算法在某种情况下会陷入局部最优解,出现早熟现象。

已有文献很难将需要空间想象力的线路设计、列车驾驶与牵引能耗之间的联系展示出来,笔者以列车牵引能耗、运行时间为优化目标,建立列车运行节能模型,采用改进多目标粒子群优化算法求解列车运行速度轨迹,并且对比不同运行策略下的节能效果。

2 列车区间运行节能优化模型

2.1 优化目标函数

以列车运行工况转换点{xi|i=1,2,…,xi∈[0,Send]}为决策变量,Send为站台指定停车位置,以牵引能耗和运行时间误差最小化为优化目标,建立优化目标函数:

minfitE(xi)=E(xi)

(1)

minfitT(xi)=|T(xi)-T0|

(2)

式中:E(xi)为区间运行总能耗;T(xi)为区间运行总时间;T0为区间计划运行时间;fitE(xi)为能耗优化目标函数;fitT(xi)为时间误差优化目标函数。

2.2 约束条件

(1) 运动约束。根据牛顿第二定律,列车运动方程为:

F(v)-B(v)-W(s,v)=m(1+γ)a(s)

(3)

式中:F(v)为牵引力;B(v)为制动力;W(s,v)为运行阻力;a(s)为运行距离s处的加速度;m为列车总质量;γ为回转质量因数,常取0.06。

以列车运行距离Δs作为迭代步长,列车在运行距离s处的加速度a(s)可由式(3)离散得到。根据动力学方程,列车运行速度、时间、位置为:

(4)

t(s+Δs)

(5)

vlimit1(s)≤v(s)≤vlimit2(s)

(6)

v(0)=v(Send)=0

(7)

|Svend=0-Send|≤ψ

(8)

式中:v(s)为运行距离s处的运行速度;vlimit1(s)为运行距离s处的运行最低限速;vlimit2(s)为运行距离s处的运行最高限速;t(s)为运行至运行距离s处的时间;Send为指定停止位置;Svend=0为实际停止位置;ψ为停车精度要求,城轨列车停车精度要求0.3 m为安全停车。

采用从区间终点反算迭代的方法求解列车制动曲线,以此求得列车制动工况转换点,保证停车精度满足要求。

(2) 受力约束。建立列车的牵引、制动、阻力模型,可以包含更多线路平纵断面的信息,更加贴近实际情况。

列车模型中的牵引力、制动力、附加力、运行阻力为:

F(v)=fF(v)

(9)

B(v)=fB(v)

(10)

wi(s)=ramp

(11)

wr(s)=A/R

(12)

ws(s)=0.000 13ls

(13)

W(s,v)=[w0(v)+wi(s)+wr(s)

+ws(s)]mg

(14)

式中:fF(v)为列车牵引特性曲线;fB(v)为列车制动特性曲线;w0(v)为基本阻力;wi(s)为单位坡道附加力;wr(s)为单位曲线附加力;ws(s)为单位隧道阻力;ramp为坡道千分数;A为阻力因数,常取600;R为轨道半径;ls为隧道长度;g为重力加速度。

(3) 运行能耗约束。根据列车牵引做功计算原理,列车在区间内运行能耗E为:

(15)

式中:F为列车在运行距离s处的牵引力。

当Δs取0.1 m时,既可以获得足够的停车精度,又可以缩短计算机求解时间,因此设Δs为0.1 m。

3 算法

3.1 改进多目标粒子群优化算法

传统多目标粒子群优化算法容易陷入局部最优解,而且最优解集多样性差,因此有必要对多目标粒子群优化算法进行改进[8]。

(1) 准对立变异粒子。为解决传统多目标粒子群优化算法存在的早熟问题,将准对立学习策略引入多目标粒子群优化算法的变异中。准对立学习策略的基本思想是在原始粒子位置的基础上,产生一个准对立粒子位置,以此扩大种群空间的覆盖范围。通过比较两个粒子位置产生的目标值,择优选择新的粒子位置。通过轮盘赌法选择是否接受较差的粒子解,帮助算法跳出局部最优。

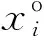
(16)

(17)

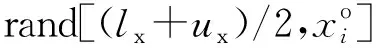
(2) 惯性权重优化。惯性权重w是多目标粒子群优化算法中的重要参数。在传统多目标粒子群优化算法中,惯性权重随迭代次数增加而线性递减。笔者通过比较当前粒子的目标值与种群的平均目标值,动态调整惯性权重w:

(18)

式中:we为粒子e的惯性权重;wmax为惯性权重最大值;wmin为惯性权重最小值;wmid为惯性权重中间值;fite,j为粒子e的第j个目标值;meanfitj为种群中所有粒子第j个目标值的平均值。

采用以上方法优化惯性权重,可以优化粒子飞行方向及飞行距离,提高算法的收敛性。

改进多目标粒子群优化算法具体步骤如下。

第1步,初始化算法参数,包括最大迭代次数、种群规模N、最优解集规模M、学习因子c1和c2,惯性权重最大值wmax、惯性权重最小值wmin、惯性权重中间值wmid。

第2步,初始化粒子e位置Xe,即工况转换点xi,初始化粒子速度Ve,即工况转换点xi改变量,计算粒子个体历史最优位置pbest,e。

第3步,根据粒子位置,计算优化目标函数值,将非支配解存入最优解集,并在最优解集中构建自适应网格计算粒子密度,选择密度较小的粒子作为种群最优解gbest。

第4步,更新种群中粒子位置和粒子速度,Ve更新为weVe+c1r1(pbest,e-Xe)+c2r2(gbest-Xe),Xe更新为Xe+Ve。

第5步,计算粒子更新后的优化目标值,以及准对立变异粒子的优化目标值,根据帕累托支配关系更新粒子个体最优位置pbest,e。

第6步,对最优解集进行更新,同时截断最优解集,保留M个最优解。

第7步,判断是否达到最大迭代次数,是则结束算法,否则跳转到第3步。

(3) 最优解选择。使用多目标粒子群优化算法求解多目标优化问题所得到的最优解集是一组解,采用模糊隶属度函数对每个解的目标值对应的隶属度进行评价,从而筛选出最优解。模糊隶属度函数um为:

um=

(19)

式中:fitem为粒子e第m个目标的函数值;maxfitm为外部档案中第m个目标对应的最大函数值;minfitm为外部档案中第m个目标对应的最小函数值。

(20)

用式(20)求解得到最优解集中每个粒子的满意度值,满意度值最大的粒子对应的解即为算法的最优解。

3.2 性能指标

收敛性和多样性是多目标粒子群优化算法中的两个重要性能指标,为了验证算法的优越性,将传统多目标粒子群优化算法、文献[8]自适应网格多目标粒子群优化算法与改进多目标粒子群优化算法进行对比。算法参数设置见表1。

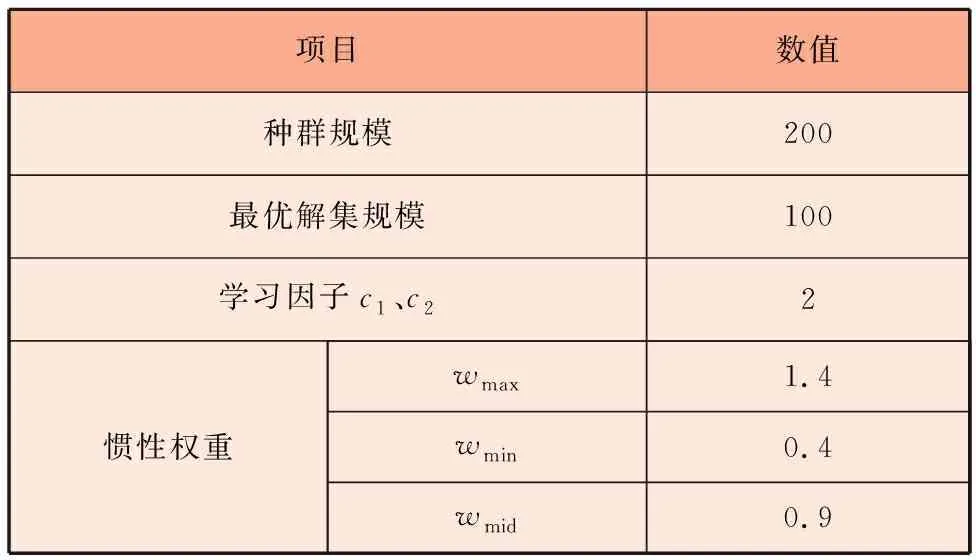
表1 算法参数设置

选用多目标粒子群优化算法性能测试中常用的ZDT1测试函数,算法最大迭代次数设为100,重复独立运行三种不同的算法30次,并求出算法的收敛性指标、多样性指标的均值和方差。收敛性指标越小,代表算法收敛性越好。多样性指标越小,代表算法多样性越好。

算法测试结果见表2。改进多目标粒子群优化算法在收敛性指标上具有较小的均值,代表算法具有更好的收敛性;在多样性指标上具有较小的均值和方差,代表算法的多样性较好。

4 实际线路仿真

4.1 列车及线路参数

选取广州地铁8号线中大—晓港区间进行仿真试验,由此验证改进多目标粒子群优化算法及列车区间运行节能优化模型的有效性。运行列车为A型列车,参数见表3。线路纵断面、曲线数据如图1所示[9]。结合约束计算式,即可计算出模型的优化目标函数。

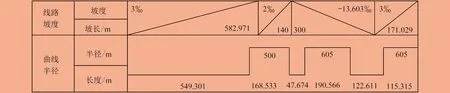
图1 线路数据

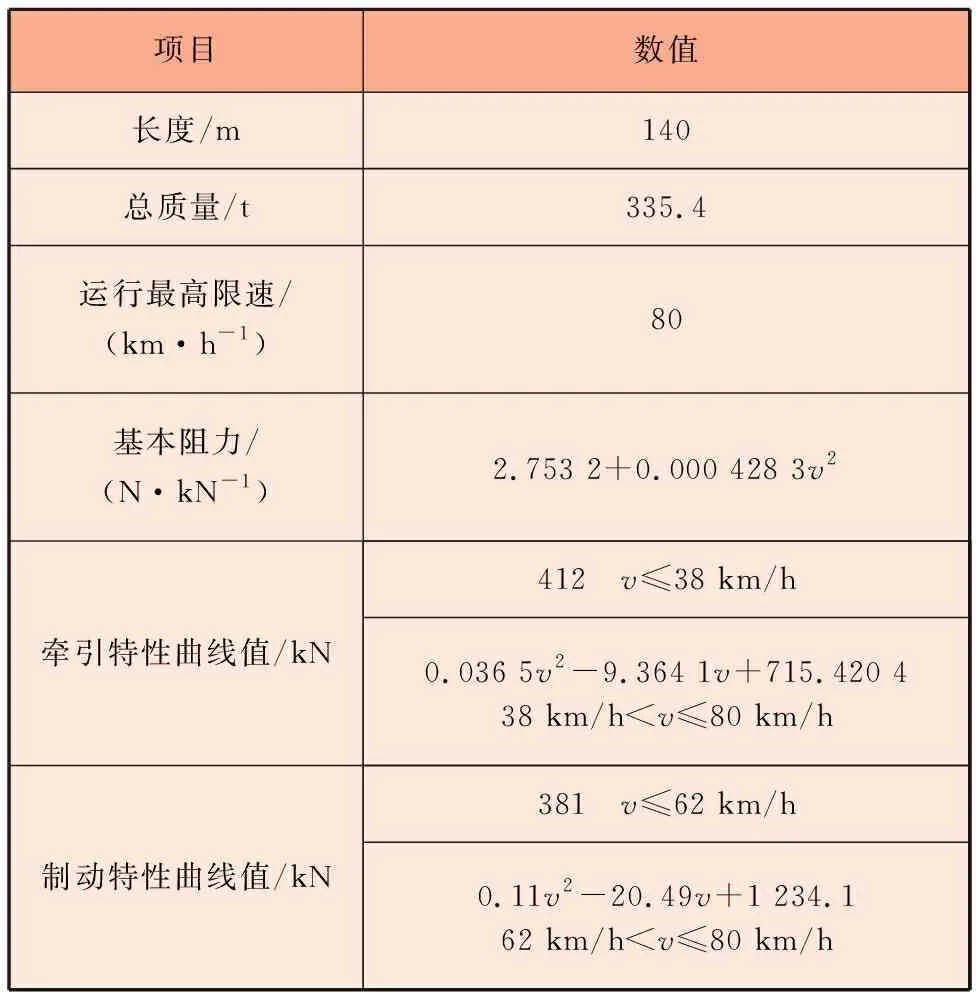
表3 A型列车参数

4.2 仿真结果

列车常采用牵引(T)、巡航(H)、惰行(C)、制动(B)四种运行工况相互组合,以保证准时、安全停靠站台。列车常用运行策略为传统四段模式,即按照T、H、C、B工况组合顺序运行。将中大—晓港区间限定运行时间设为100 s,改进多目标粒子群优化算法迭代次数设为20,种群规模设为100,最优解集设为50,求解THCB、TCHCB、TCTCB三种运行策略的最优解。算法结果见表4,三种运行策略的最优速度曲线如图2所示。

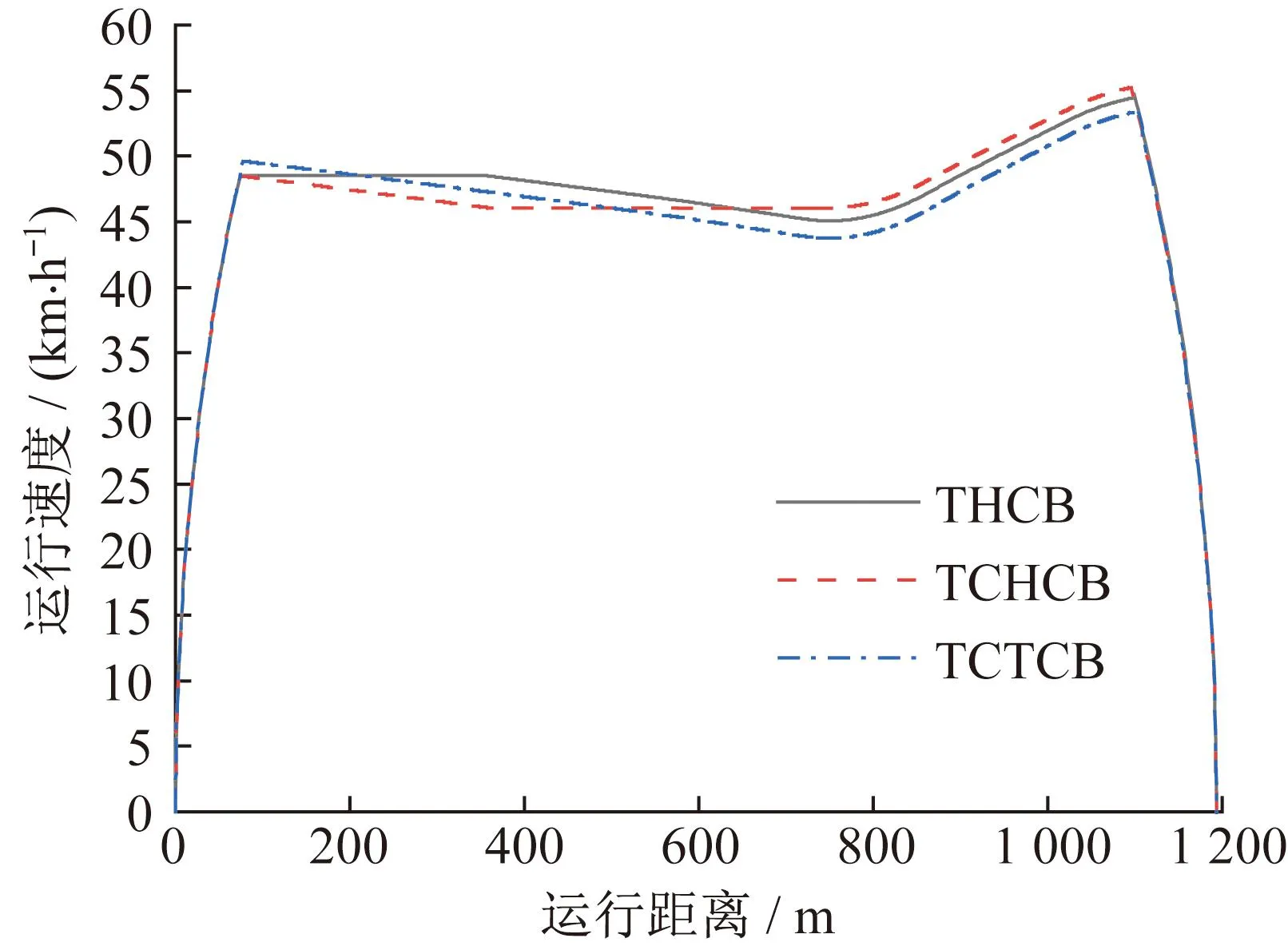
图2 不同运行策略最优速度曲线

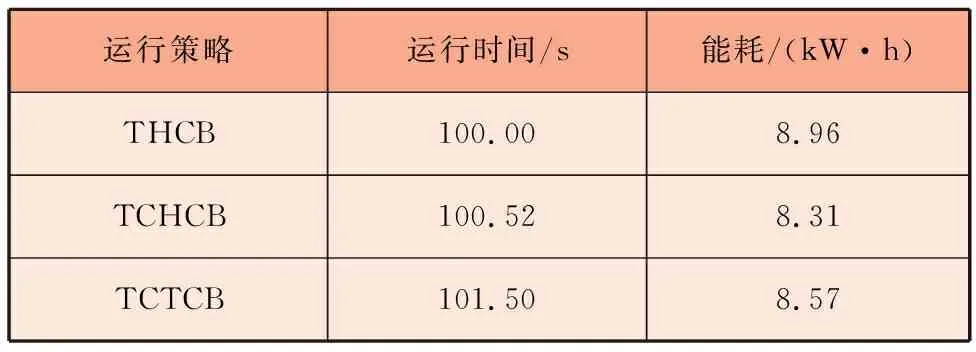
表4 仿真算法结果

在运行时间方面,三种运行策略均可以满足列车运行时间误差要求,进一步证明了改进多目标粒子群优化算法求解列车区间运行节能优化模型的有效性。在运行能耗方面,TCHCB运行策略比THCB运行策略增加惰行工况,列车的运行能耗从8.96 kW·h减少至8.31 kW·h,降幅为7.25%。同时,TCTCB运行策略也比THCB运行策略节能4.4%,说明在列车运行期间适当增加惰行的次数,可以减少列车的运行能耗。TCTCB运行策略与TCHCB运行策略相比,列车的运行能耗从8.31 kW·h增加至8.57 kW·h,增幅为3.1%。结合图2可以发现,TCTCB运行策略拥有更长的牵引距离和更高的最大牵引速度,由此才能抵消惰行工况带来的速度衰减,在规定运行时间范围内到达指定车站。

5 结束语

对于城市轨道交通中列车节能方法的问题,建立列车区间运行节能优化模型,采用改进多目标粒子群优化算法求解不同运行策略下的列车运行速度曲线,并得出结论。

针对传统多目标粒子群优化算法容易陷入局部最优解等问题,对算法进行改进。采用准对立学习策略对粒子进行变异优化,采用当前粒子的目标值与种群的平均目标值动态调整惯性权重。

通过ZDT1测试函数检验算法性能,结果显示,相比传统多目标粒子群优化算法,改进多目标粒子群优化算法拥有更好的收敛性和多样性。

采用改进多目标粒子群优化算法求解列车区间运行节能优化模型,建立满意度评价方法获得最优运行曲线。采用实际线路数据进行仿真,对比不同运行策略的节能效果。结果显示,在传统四段运行策略中增加惰行工况,变为TCHCB运行策略,可以明显减少运行能耗,节能率为7.25%。当然,另一种TCTCB运行策略需要更长的牵引距离,才能在规定时间内到达车站,节能率为4.4%。