隧道减光格栅段全天候路面照度计算模型

吴宣莹，杨继厅，李正华，康 诚，张 驰，吴 珂，5

(1.浙江大学浙江省海洋岩土工程与材料重点实验室，浙江 杭州 310058；2. 浙江大学平衡建筑研究中心，浙江 杭州 310007；3.浙江数智交院科技股份有限公司，浙江 杭州 310006；4. 绍兴市柯诸高速公路有限公司，浙江 绍兴 312000；5.浙江大学中原研究院，河南 郑州 450000)

引言

隧道洞口设置减光格栅，不仅有利于缓和隧道内外光环境的剧烈过渡，缩短驾驶人的视觉适应时间，而且可降低入口段亮度需求，节省隧道照明系统一次性投入和运营成本，已在我国隧道建设中逐步推广应用[1-3]。

在自然光源照射下，隧道减光格栅段路面亮暗区域照度差异大，这种光场的不均匀分布会降低驾驶员的视觉功效。针对隧道减光格栅段的光环境，一部分学者采用比尺模型试验方法获得了减光格栅下方路面光场分布。玮宝等[4]和Gil-Martín等[5]通过搭建减光格栅模型，测量获得了6月份晴天中午时刻下路面照度随格栅间距的变化规律。吴刚等[6]以港珠澳大桥隧道为对象，制作了1/43的减光格栅模型，实测9月某天11：00—13：00时段内的路面亮度。由于存在测量周期长、结构参数不便调节和环境条件无法更改等局限，比尺模型试验方法往往难以获得减光格栅段路面光场的长时序分布特征。

数学模型计算方法可以较为准确地计算长时间序列下的路面光场分布，在隧道减光格栅段光环境研究方面得到了广泛的应用。Pea-García等[7]基于太阳运行轨迹，利用太阳光线、减光格栅和侧墙之间的角度关系，建立了路面平均照度和亮暗区域面积变化的理论预测模型，但该模型忽略了天空散射对路面暗区照度的影响。Cantisani等[8，9]针对可完全遮挡住太阳直射光的减光格栅，提出了仅考虑天空散射的隧道减光格栅段路面照度计算方法，可用于分析晴天时减光格栅参数对路面光效的影响。应当指出，散射对路面照度的影响超过25%[10]，计算路面照度时应同步考虑直射和散射的共同作用。此外，天气对路面光场分布影响显著，多云、阴天时路面平均照度相较晴天降低15%～60%[11]，而已有模型均只适用于标准晴天。

因此，本文将太阳辐射理论和CIE天空模型相结合以同步考虑太阳直射和天空散射，利用大气消光系数、太阳照度参数和天空元参数反映天气因素的影响，构建了隧道减光格栅段全天候路面照度计算模型，为隧道减光设计和光环境评价提供参考依据。

1 模型构建

对于隧道减光格栅段路面，入射光包含太阳直射光和天空散射光，减光格栅对光线起到物理遮挡作用。因此，首先计算直射和散射照度，然后考虑格栅遮挡效果，最终形成减光格栅段全天候路面照度计算模型。

1.1 太阳直射照度

太阳光入射到地面的过程中，会受到日地距离和地球大气等因素影响，导致强度逐渐衰减[12]。由于地球绕太阳公转轨道为椭圆形，日地距离会随时间改变，从太阳到达地球外表面的照度Ext需根据日地距离进行修正，Ext的计算式[13]为：

Ext=Esc[1+0.034cos(2π(J-2)/365)]

(1)

式中，Esc为太阳照度常数，指太阳处的太阳辐射照度，常取133.1 klx；J为日期。

光线从地外穿过大气层的过程中将发生衰减，最终抵达地面的太阳光强度为法向太阳照度Edn。由于太阳光并非垂直入射地面，因此路面的太阳直射照度ED应为Edn的垂直分量，即：

ED=Ednsinαt

(2)

Edn=Exte-c/sinαt

(3)

式中，αt为太阳高度角，是太阳光入射方向和地平面之间的夹角(rad)，如图1所示；c为大气消光系数，受大气污染程度和气象要素影响，可通过实测[14]或模型计算[15]获得。

图1 太阳和天空元角度Fig.1 Angles of sun and sky element

αt表征了太阳位置，可通过当地纬度lsite、太阳赤纬δ、太阳时t计算得到[13]：

αt=arcsin[sinlsitesinδ-coslsitecosδcos(πt/12)]

(4)

1.2 天空散射照度

太阳光穿过大气层时，经空气分子和气溶胶等反射和折射形成散射光，从而使天空产生不均匀的亮度分布。天空可视为由若干天空元组成的发光半球，天空半球上任意天空元的亮度取决于天顶亮度Lz以及天空元、天顶、太阳三者之间的相对位置。以天空元P为例，其亮度LP计算式[16]为：

(5)

式中，Lz为天顶亮度(kcd/m2)，由天空水平照度Ekh和天顶亮度系数ZL决定，可分别由式(6)、(7)计算得到；ζ、γ、Z0分别为天空元和天顶之间的夹角、天空元和太阳之间的夹角、天顶和太阳之间的夹角(rad)，如图1所示；f(γ)、f(Z0)为散射指标函数、φ(ζ)为亮度梯度函数，可由式(8)～(10)计算得到。

Lz=EkhZL

(6)

Ekh=A+BsinCat

(7)

f(γ)= 1+e·cos2γ+c·[exp(dγ)-exp(dπ/2)]

(8)

f(Z0)= 1+e·cos2Z0+c·[exp(dZ0)-exp(dπ/2)]

(9)

φ(ζ)=1+a·exp(b/cosζ)

(10)

式中，A、B、C为太阳照度参数，取值见表1。a、b、c、d、e为天空元参数，反映了气象因素的影响，CIE提供了15种天空类型下的天空元参数取值[17]。

表1 太阳照度参数

每一个天空元均可视为有一定面积的点光源，其照射到地面的光强即为天空元散射照度。根据距离平方反比定律[18]，天空元P的散射照度ESP计算式为：

ESP=LP(A/r2)cosζP

(11)

式中，A=r2dωdθ，为天空元面积(m2)；r为天空元到地面的距离(m)；ω、θ为天空元与地面的夹角(rad)。

1.3 路面光场分布

任意光源i(i=0时为太阳，i=1，2，…，n时为天空元)产生的光线经过减光格栅时，一部分会被格栅遮挡，剩余部分则照射到路面。被光源i照射到的路面区域为ULi，未被照射到的区域为UDi，如图2(a)所示。以沿行车方向为x轴，垂直行车方向为y轴，建立直角坐标系，ULi、UDi如图2(b)所示。

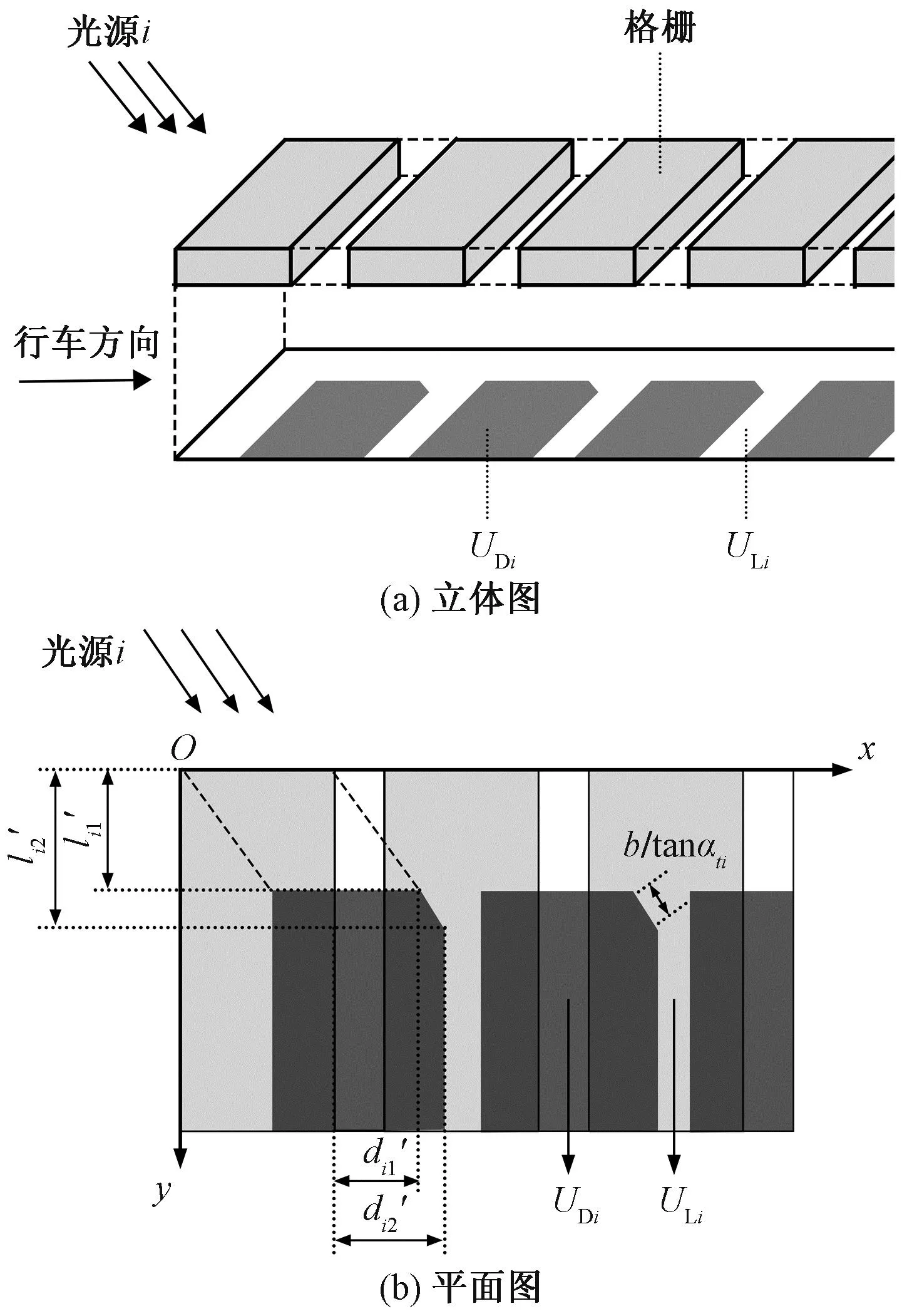
图2 隧道减光格栅段路面区域划分Fig.2 Regional division of pavement under a tunnel pergola

当光源i方位角αsi⊂(0，π/2)时，UDi范围如式(12)所示，其余区域为ULi。当光源改变时，同理可获得对应的ULi、UDi范围。

(12)

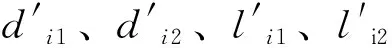
(13)

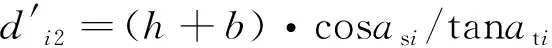
(14)

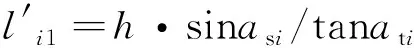
(15)

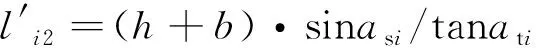
(16)

式中，h为格栅高度(m)；ati为光源i的高度角(rad)；b为格栅厚度(m)。

利用式(1)～(11)，可计算光源i在ULi产生的照度Ei；由于UDi未被光源i照射到，该区域内的照度为0，因此，光源i在路面形成的照度分布Ei(x，y)如下。

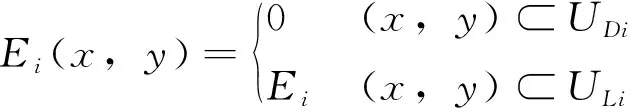
(17)

进一步将所有光源(i=0～n)产生的Ei(x，y)进行叠加，如图3所示，即可获得减光格栅段路面的照度分布E(x，y)。

图3 路面照度分布计算示意图Fig.3 The calculation of pavement illuminance distribution

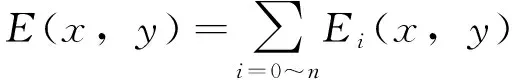
(18)

2 结果分析

利用实测数据验证本文构建计算模型的适用性和精度。实测隧道为紫金港路隧道(120 °N，30°E)，全长2 150 m，双向四车道，设计速度为60 km/h，单洞宽9.75 m、高5 m。隧道洞口设减光格栅，格栅宽度0.5 m、间距3.5 m、厚度1 m，如图4所示。分别对晴天(6月22日、23日)、多云(6月26日、27日)、阴天(6月15日、16日)条件下6：00—20：00时段格栅下方的路面照度进行测量。测点位于路面中线，间隔1 m。测量采用远方Z-10智能照度计，精度为2%。各测点测三次取平均值，以避免测量误差。

图4 紫金港路隧道减光格栅段Fig.4 The tunnel pergola of Zijingang Road

2.1 天空元数量的影响

受太阳位置和大气条件影响，天空各点亮度并不相同，为描述天空亮度的不均匀分布，可根据区域不重叠、均匀分布和划分区域关于天顶对称等原则[19]，将天空划分为有限的天空元。在进行天空亮度的测量和计算时，通常的做法是划分为8层共145个天空元[20]。增加天空元数量会提高模型精度，但也会加大计算量，根据划分原则，设置如表2所示的工况以对比天空元数量对模型精度的影响。

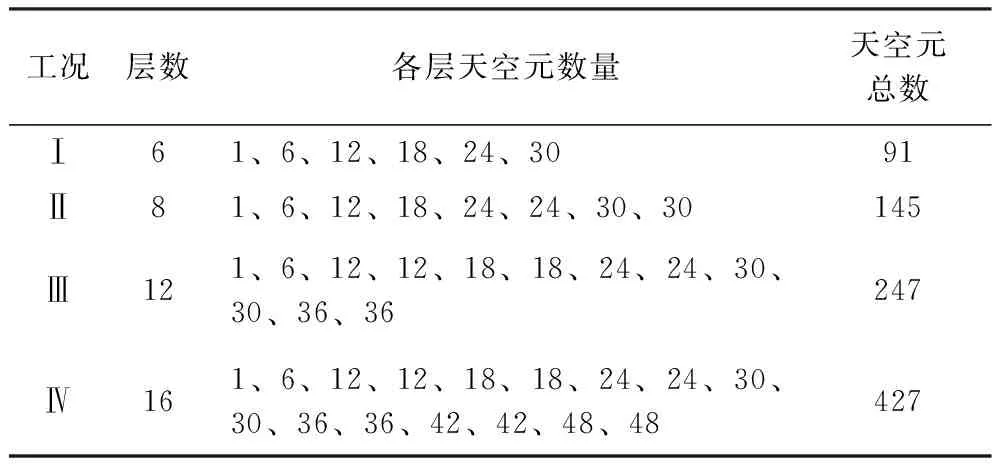
表2 天空元数量工况

图5为夏至日(6月22日)12：00减光格栅段路面沿行车方向的照度分布。可以看出，随着天空元数量的增加，路面亮区和暗区的照度计算值均增大且更接近实测值。当天空被划分为12层、天空元数量达到247个后，进一步增加天空元数量对亮、暗区域照度计算值的影响将极为有限。

图5 减光格栅段沿行车方向路面照度分布Fig.5 Pavement illuminance distribution along the driving direction under the tunnel pergola

表3为不同天空元数量下照度计算值与实测值之间的平均偏差百分比M。可以看出，路面亮区和暗区的M均随着天空元数量的增加而减小。对于路面亮区，当天空元数量达到145时，M<5%，且进一步增加天空元数量到427时，M仅从4.3%降低至3.8%。而对于路面暗区，当天空元数量达到247时，M<5%。可见，尽管天空元数量的变化仅影响天空散射，但由于减光格栅段路面亮区同时受太阳直射和天空散射的影响，而暗区仅受天空散射作用。因此，路面暗区照度计算值受天空元数量的影响更大。

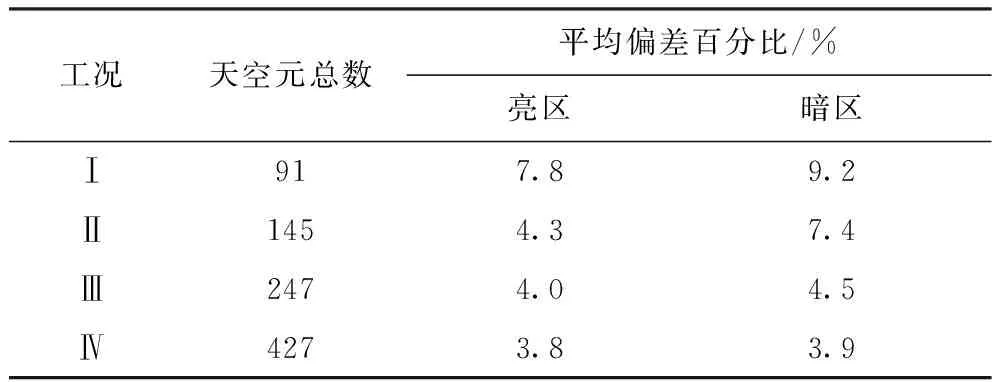
表3 平均偏差百分比

综合考虑计算精度和效率，为准确获得隧道减光格栅段路面照度分布，应用本文模型建议天空划分为12层共247个天空元。

2.2 季节因素的影响

杨公侠等[11]搭建了上海打浦路隧道减光格栅的1/10比尺模型，测量了不同季节晴天时格栅下方路面亮区照度，图6为预测结果与实测数据的对比。可以看出，随着太阳的东升西落，路面亮区照度在一天中呈现出先增大后减小的变化规律。其中，夏至照度最高、冬至最低，春分、秋分介于夏至和冬至之间。春分、夏至、秋分、冬至下照度计算值与实测值间的平均偏差百分比M分别为6.8%、3.2%、5.9%、7.6%，夏至时误差最小，这是因为夏至时路面照度大，测量误差造成的影响小。本文构建的模型能够准确捕捉不同季节时路面亮区照度分布特征，模型预测结果与文献实测数据吻合良好。

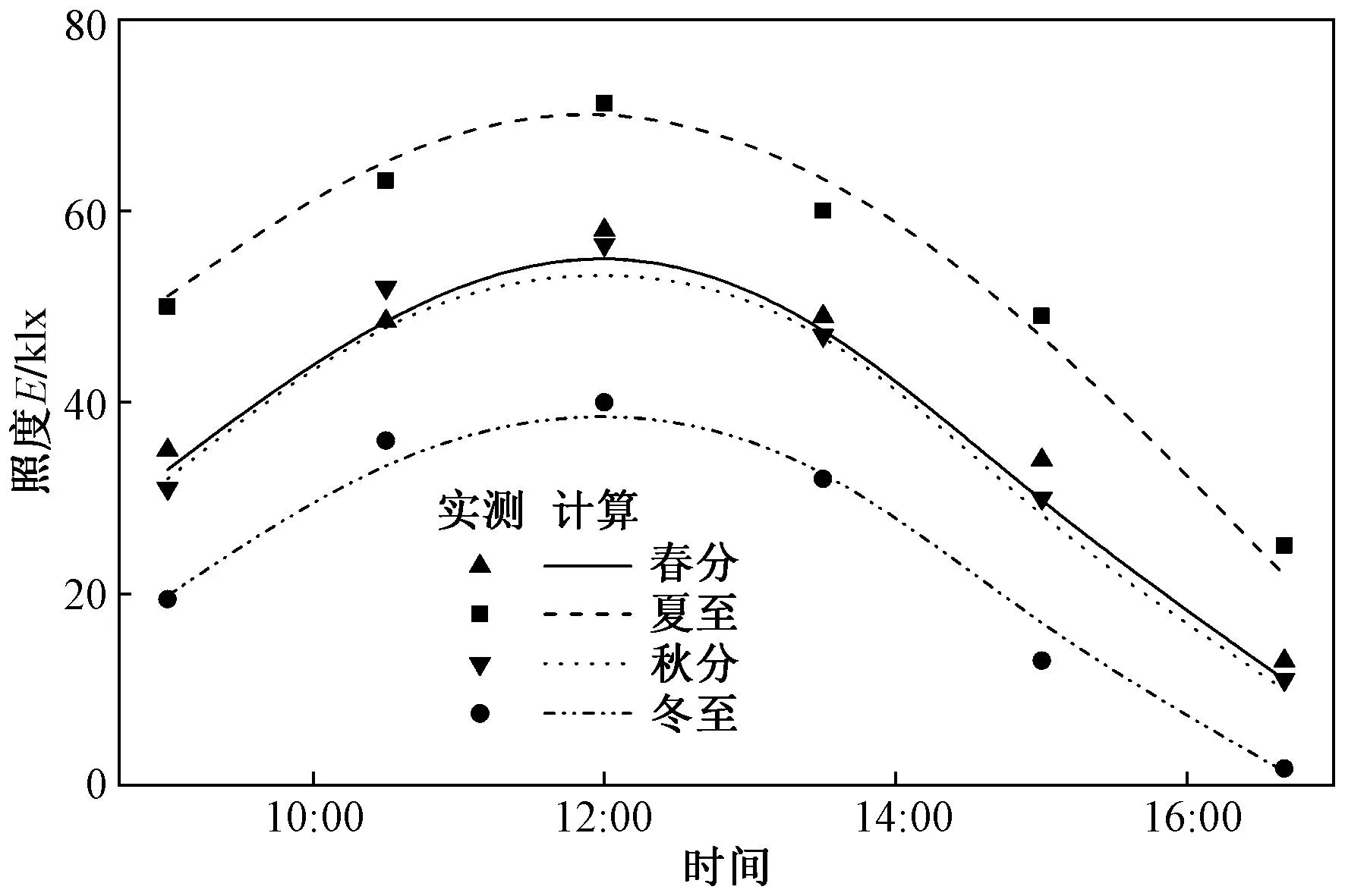
图6 减光格栅段路面亮区照度Fig.6 Pavement illuminance of bright region under the tunnel pergola

2.3 天气因素的影响

图7为夏季时不同天气下紫金港路隧道减光格栅下方的路面照度分布。

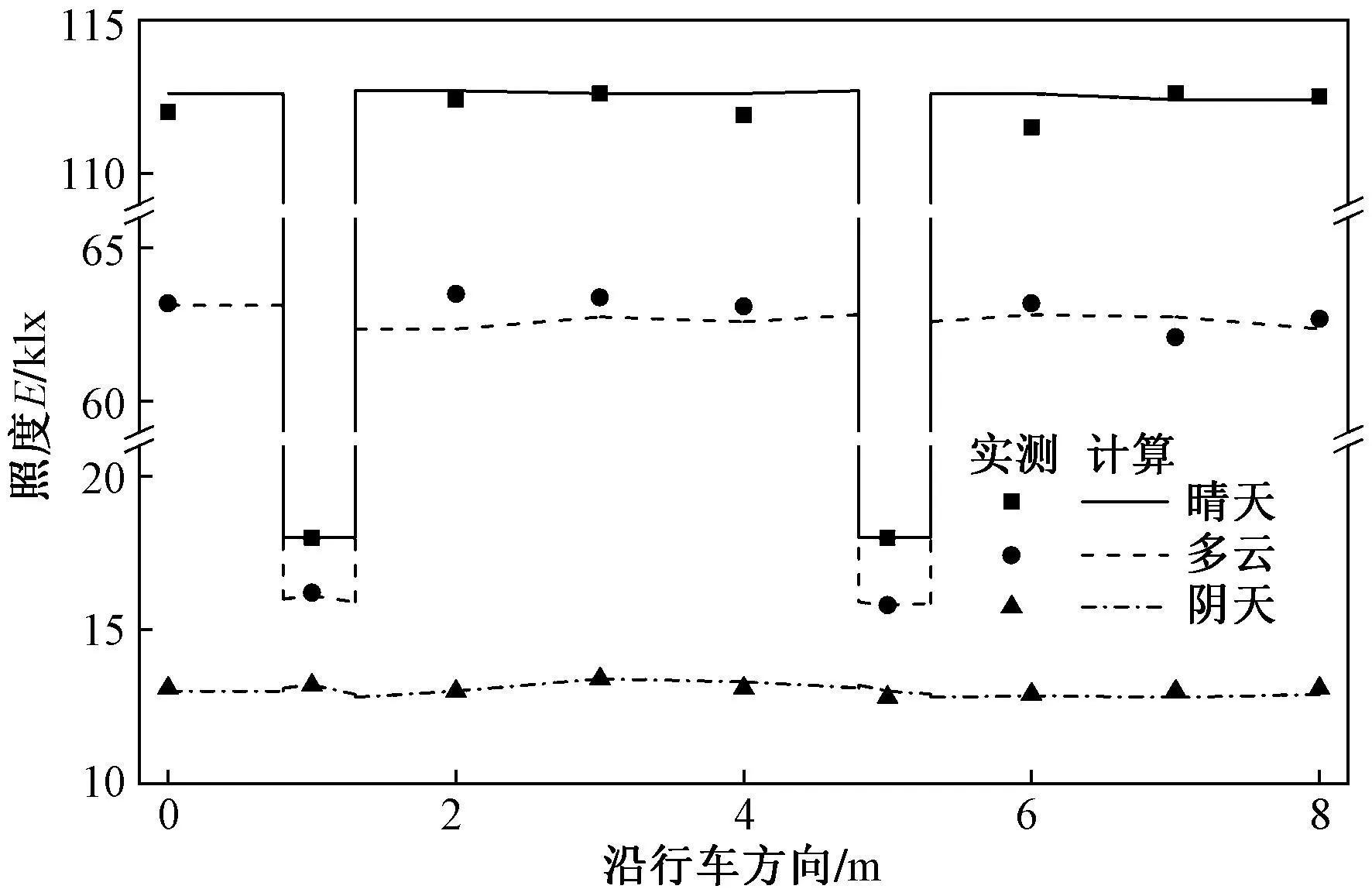
图7 减光格栅段路面沿行车方向照度分布Fig.7 Pavement illuminance distribution along the driving direction under the tunnel pergola

由图7可知，模型计算结果与实测数据吻合良好，平均偏差百分比M在多云时为7.6%，在晴天和阴天时仅为2.3%、3.4%。相较于晴天，多云和阴天路面亮区照度下降幅度可达43.9%、88.3%，而暗区下降幅度分别为11.1%、18.1%。多云和阴天时路面亮暗区照度差更小，路面均匀度更高。可见，本文模型可以反映出不同天气下路面亮暗区照度和均匀度的变化特点。

3 结论

本文基于太阳辐射理论和CIE天空亮度分布函数构建了同步考虑太阳直射和天空散射的隧道减光格栅段全天候路面照度计算模型，模型预测结果与实测数据吻合良好(M<8%)，可准确捕捉不同季节和天气条件下的路面照度分布特征和时变特性。

增加天空元数量可提升本文模型的计算精度，且对路面暗区照度计算值的影响更大。综合考虑精度与计算效率，建议应用本模型时天空划分为12层共247个天空元。