24p阶群的构造
2024-01-08陈松良莫贵圈
陈松良,李 斌,莫贵圈
(贵州师范学院数学与大数据学院,贵州 贵阳 550018)
有限群的同构分类,一直是人们关心的问题。设p,q是不同的素数,文[1]与[2]分别确定了p3q阶群和p3q2阶群的构造。当p,q是不同的奇素数时,文[3]完成了p3q3阶群的同构分类。文[4]分析了无三次因子阶群的结构信息并给出了在同构意义上构造这类群的一个算法,文[5]对无三次因子阶群的结构信息给出了更细致准确的描述和刻画,文[6]对无四次因子阶群的结构信息给出了描述和刻画。当p>3为奇素数时,本文研究了阶为24p的有限群G的同构分类,得到了G的各种互不同构的类型,从而推广了文[7]、[8]的结果,并指出了文[7]、[8]中存在的错误。
在本文中,Cn表示n阶循环群,Epn表示pn阶初等交换群,A∶B表示群A被群B的半直积,|G|,|g|分别表示群G与元素g的阶,记xg=g-1xg,其他符号的意义请读者参看文献[9-11]。此外,为简化叙述,当一个群中两个生成元交换时,在生成关系中,不再加以说明。
1 主要结果
定理1 设p是奇素数且p>3但p≠5或7,G是24p阶群,那么:(i)当p≡1(mod 24)时,G共有64个互不同构的类型;(ii)当p≡13(mod 24)时,G共有61个互不同构的类型;(iii)当p≡17(mod 24)时,G共有46个互不同构的类型;(iv)当p≡11,23(mod 24)时,G共有39个互不同构的类型;(v)当p≡7,19(mod 24)但p≠7时,G共有54个互不同构的类型;(vi)当p≡5(mod 24)但p≠5时,G共有44个互不同构的类型。
2 定理1的证明
以下恒设p是奇素数且p>3但p≠5或7,G是24p阶群。
引理1 不存在阶为 264=24·11 的单群。
证明:见文献[9]第78页例5.15。
引理2 设H是24阶群,则H必同构于下列15种类型之一[12]:
(a)H1=a||a|=24;
(b)H2=a,b||a|=12,|b|=2,ab=a;
(c)H3=a,b,c||a|=6,|b|=|c|=2,ab=ac=a,bc=b;
(d)H4=a,b||a|=3,|b|=8,ab=a-1;
(e)H5=a,b,c||a|=3,|b|=4,|c|=2,ab=a-1,ca=cb=c;
(f)H6=a,b,c||a|=3,|b|=2,|c|=4,ab=a-1,ca=cb=c;
(g)H7=(a:b)×c×d,其中|a|=3,|b|=|c|=|d|=2,ab=a-1;
(h)H8=a,b||a|=6,|b|=4,ba=b-1;
(i)H9=a,b,c||a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1;
(j)H10=a,b||a|=12,|b|=2,ab=a-1;
(k)H11=b,c||b|=|c|=4,b2=c2,bc=b-1×a||a|=3;
(l)H12=a,b,c||a|=3,|b|=|c|=4,b2=c2,ab=a,ac=a-1,bc=b-1;
(m)H13=a,b,c||a|=3,|b|=|c|=4,b2=c2,bc=b-1,ba=c,ca=bc;
(n)H14=a,b,c||a|=3,|b|=|c|=2,ba=c,ca=bc×d||d|=2
(o)H15=a,b,c,d||a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,ad=a-1,bd=c,cd=b.
引理3 设G是264=24·11阶群,则G的 Sylow 11-子群是G的正规子群。
证明:若G的Sylow 11-子群P不正规,则由Sylow定理[10]39可知,G的Sylow 11-子群的个数是12,从而NG(P)是22阶群。又由引理1知G的极小正规子群N是3阶循环群或阶不大于8的初等交换2-群,于是再由Sylow定理[10]39可知P◁NP,因而N⊂NG(P)。但NG(P)是22阶群,所以必有|N|=2。 由此又易知NG(P)是交换群,从而由Burnside定理[11]169知,G有正规11-补K,且显然|K|=24。 又由引理2不难推出,任何24阶群都不可能有11阶的自同构,因而P只能平凡作用在K上,从而P◁G,矛盾。
显然,由Sylow定理及其推论知,当p>11时,G的Sylowp-子群P必正规。从而在本文讨论的范围内,G的Sylowp-子群P总是正规的,且G总是可解群。于是再由Schur-Zassenhaus定理[10]246知,P在G中有补子群H。显然H是24阶群,而由引理2得H有15种互不同构的类型,因此对群G可作如下讨论:
引理4 设p是奇素数,且p>3但p≠5或7,σ为模p的一个原根。如果24p阶群G的Sylowp-子群P=x||x|=p的补子群H是交换群:H1、H2、H3,那么:

G恰有20个互不同构的类型:
G1=x||x|=24p;
G2=x×y,其中|x|=12p,|y|=2;
G3=x×y×z,其中|x|=6p,|y|=
|z|=2;
G4=x:a,其中|x|=p,|a|=24,
xa=x-1;
G5=x:a,其中|x|=p,|a|=24,
xa=xr8;
G6=x:a,其中|x|=p,|a|=24,
xa=xr6;
G7=x:a,其中|x|=p,|a|=24,
xa=xr4;
G8=x:a,其中|x|=p,|a|=24,
xa=xr3;
G9=x:a,其中|x|=p,|a|=24,
xa=xr2;
G10=x:a,其中|x|=p,|a|=24,
xa=xr;
G11=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=xr2;
G12=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=xr4;
G13=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=xr6;
G14=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=xr8;
G15=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=x-1;
G16=(x:b)×a,其中|x|=p,|a|=12,|b|=2,xb=x-1;
G17=x:(a×b),其中|x|=p,|a|=12,|b|=2,xa=xr8,xb=x-1;
G18=(x:a)×b×c,其中|x|=p,|a|=6,|b|=|c|=2,xa=xr4;
G19=(x:a)×b×c,其中|x|=p,|a|=6,|b|=|c|=2,xa=xr8;
G20=(x:a)×b×c,其中|x|=p,|a|=6,|b|=|c|=2,xa=x-1.
(ii) 当p≡13(mod 24)时,则G恰有18个互不同构的类型,即(i)中除了G8和G10外的其余18种构造。
(iii)当p≡17(mod 24)时,则G恰有10个互不同构的类型,即(i)中的G1、G2、G3、G4、G6、G8、G13、G15、G16、G20。
(iv)当p≡7,19(mod 24)时,则G恰有14个互不同构的类型,即(i)中除了G6、G8、G9、G10、G11和G13外的其余14种构造。
(v)当p≡5(mod 24)时,则G恰有9个互不同构的类型,即(i)中的G1、G2、G3、G4、G6、G13、G15、G16、G20。
(vi)当p≡11,23(mod 24)时,则G恰有7个互不同构的类型,即(i)中的G1、G2、G3、G4、G15、G16、G20。
证明 (i)如果G是交换群,那么容易得到G有3种互不同构的类型:G1、G2、G3。 如果G不是交换群,那么G=P∶H,且H非平凡作用在P上,即H/CH(P)同构于Aut(P)的一个非单位子群。设σ是模p的一个原根,则Aut(P)=σ是p-1阶循环群,所以H/CH(P)是一个不等于1的循环群。
1)当H≅H1时,CH(P)可取为a2、a3、a4、a6、a8、a12、1,由此可得G的7个互不同构的非交换群:G4、G5、…、G10。
2)当H≅H2时,CH(P)可取为b、a6,b、a4,b、a3,b、a2,b、a、a3,它们分别同构于:C2、C2×C2、C3×C2≅C6、C4×C2、C6×C2、C12、C4,由此可得G的7个构造:G11、G12、…、G17。 显然,这7个群的中心互不同构,所以它们是互不同构的7个24p阶群。
3)当H≅H3时,CH(P)可取为b,c、a3,c、a3,b,c、a2,b,c、a,c。但b,c≅C2×C2≅a3,c、a3,b,c≅C2×C2×C2≅E8、a2,b,c≅C6×C2,所以当CH(P)分别取为b,c、a3,b,c、a2,b,c时,可得G的3个互不同构的非交换群:G18、G19、G20。
如果取CH(P)=a,c,那么必有xb=x-1,于是得G的构造为:
G=(x:b)×a×c,其中|x|=p,|a|=6,|b|=|c|=2,xb=x-1。
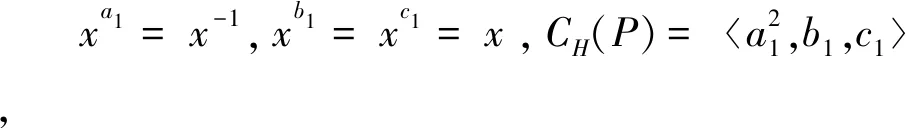
如果取CH(P)=a3,c,那么可设xa=xr8,xb=x-1,于是得G的构造为:
G=(x:(a×b))×c,其中|x|=p,|a|=6,|b|=|c|=2,xa=xr8,xb=x-1。
在上述构造中,若令a1=a5b,b1=a3,c1=c,则xa1=xr4,xb1=xc1=x,CH(P)=b1,c1,由此不难看出上述构造与G18同构。
(ii)当p≡13(mod 24)时,H/CH(P)不可能是24或8阶循环群,因此这时G没有(i)中的构造G8和G10,从而G恰有18个互不同构的类型。
(iii)当p≡17(mod 24)时,H/CH(P)不可能是24、12、6或3阶循环群,因此这时G没有(i)中的构造G5、G7、G9~G12、G14、G17、G18和G19,从而G恰有10个互不同构的类型。
(iv)当p≡7,19(mod 24)时,H/CH(P)不可能是24、12、8或4阶循环群,因此这时G没有(i)中的构造G6、G8、G9、G10、G11和G13,从而G恰有14个互不同构的类型。
(v)当p≡5(mod 24)时,H/CH(P)不可能是24、12、8、6或3阶循环群,因此这时G没有(i)中的构造G5、G7~G12、G14、G17、G18和G19,则G恰有9个互不同构的类型。
(vi)当p≡11,23(mod 24)时,H/CH(P)只可能是1或2阶循环群,因此这时G没有(i)中的构造G5~G14、G17~G19,则G恰有7个互不同构的类型。
引理5 设p是奇素数,且p>3但p≠5或7,σ为模p的一个原根。 如果24p阶群G的Sylowp-子群P=x||x|=p的补子群H是非交换群:H4、H5、H6、H7,那么:

G1=x×(a:b),其中|x|=p,|a|=3,|b|=8,ab=a-1;
G2=x×(a:b)×c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1;
G3=x×(a:b)×c,其中|x|=p,|a|=3,|b|=2,|c|=4,ab=a-1;
G4=x×(a:b)×c×d,其中
|x|=p,|a|=3,|b|=|c|=|d|=2,ab=a-1;
G5=(x×a):b,其中|x|=p,|a|=3,|b|=8,ab=a-1,xb=xr;
G6=(x×a):b,其中|x|=p,|a|=3,|b|=8,ab=a-1,xb=xr2;
G7=(x×a):b,其中|x|=p,|a|=3,|b|=8,ab=a-1,xb=x-1;
G8=((x×a):b)×c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,xb=xr2;
G9=((x×a):b)×c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,xb=x-1;
G10=(x:c)×(a:b),其中|x|=p,
|a|=3,|b|=4,|c|=2,ab=a-1,xc=x-1;
G11=((x×a):b)×c,其中|x|=p,|a|=3,|b|=2,|c|=4,ab=a-1,xb=x-1;
G12=(x:c)×(a:b),其中|x|=p,
|a|=3,|b|=2,|c|=4,ab=a-1,xc=xr2;
G13=(x:c)×(a:b),其中|x|=p,
|a|=3,|b|=2,|c|=4,ab=a-1,xc=x-1;
G14=(x×a):(b×c),其中|x|=p,|a|=3,|b|=2,|c|=4,ab=a-1,ac=a,xb=xc=x-1;
G15=((x×a):b)×c×d,其中|x|=p,|a|=3,|b|=|c|=|d|=2,ab=a-1,xb=x-1;
G16=(x:d)×(a:b)×c,其中|x|=p,|a|=3,|b|=|c|=|d|=2,ab=a-1,xd=x-1.
(ii)当p≡5,13(mod 24)时,则G恰有15个互不同构的类型,即(i)中除了G5外的其余15种构造。
(iii)当p≡7,11,19,23(mod 24)时,则G恰有12个互不同构的类型,即(i)中的G1、G2、G3、G4、G7、G9、G10、G11、G13、G14、G15、G16。
证明 (i)如果H平凡作用在群P上,那么容易得到G有4种互不同构的类型:G1、G2、G3、G4。 如果H非平凡作用在群P上,那么G=P∶H,即H/CH(P)同构于Aut(P)的一个非单位子群。设σ是模p的一个原根,则Aut(P)=σ是p-1阶循环群,所以H/CH(P)是一个不等于1的循环群。
1)当H≅H4时,CH(P)可取为a、a,b4、a,b2,由此可得G的3个互不同构的构造:G5、G6、G7。
2)当H≅H5时,CH(P)可取为a,c、a,b2,c、a,b,且易知a,c≅C6、a,b2,c≅C6×C2、a,b≅C3:C4是非交换群。 于是a,c、a,b2,c、a,b是两两互不同构的,从而得G的3个互不同构的构造:G8、G9、G10。
3)当H≅H6时,CH(P)可取为a,c、a,b、a,b,c2、a,bc,且易知a,c≅C12、a,b≅C3:C2≅S3、a,b,c2≅S3×C2、a,bc≅C3:C4。 于是a,c、a,b、a,b,c2、a,bc是两两互不同构的,从而得G的4个互不同构的构造:G11、G12、G13、G14。
4)当H≅H7时,CH(P)可取为a,c,d、a,b,c,而a,c,d≅C6×C2,a,b,c≅S3×C2,由此可得G的2个互不同构的构造:G15、G16。
(ii)当p≡5,13(mod 24)时,H/CH(P)不可能是8阶循环群,因此这时G没有(i)中的构造G5,从而G恰有15个互不同构的类型。
(iii)当p≡7,11,19,23(mod 24)时,H/CH(P)不可能是8阶或4阶循环群,因此这时G没有(i)中的构造G5、G6、G8、G12,从而G恰有12个互不同构的类型。
引理6 设p是奇素数,且p>3但p≠5或7,σ为模p的一个原根。如果24p阶群G的Sylowp-子群P=x||x|=p的补子群H是非交换群:H8、H11、H13、H14,那么:
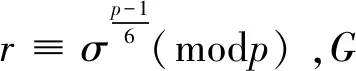
G1=x×a×b,c,其中|x|=p,|a|=3,|b|=4,|c|=2,bc=b-1;
G2=x×a×b,c,其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1;
G3=x×(b,c:a),|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,ba=c,ca=bc;
G4=x×((b×c):a)×d,其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc;
G5=(x×b):a,其中|x|=p,|a|=6,|b|=4,xa=xr,ba=b-1;
G6=(x×b):a,其中|x|=p,|a|=6,|b|=4,xa=xr2,ba=b-1;
G7=(x×b):a,其中|x|=p,|a|=6,|b|=4,xa=x-1,ba=b-1;
G8=x:(b:a),其中|x|=p,|a|=6,|b|=4,ba=b-1,xa=x,xb=x-1;
G9=x:(b:a),其中|x|=p,|a|=6,|b|=4,ba=b-1,xa=xr2,xb=x-1;
G10=x:(a×b,c),其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,xa=xr2,xb=x,xc=x-1;
G11=(x:a)×b,c,其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,xa=xr2;
G12=(x×a×b):c,其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,xc=x-1,ac=a,bc=b-1;
G13=(x×b,c):a,其中|x|=p,|a|=3,|b|=2,|c|=4,b2=c2,bc=b-1,xa=xr2,ba=b,ca=c;
G14=x:(((b×c):a)×d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,xa=xr2,xb=xc=x,xd=x-1;
G15=x:(((b×c):a)×d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,xa=xr2,xb=xc=xd=x;
G16=x:(((b×c):a)×d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,xa=xb=xc=x,xd=x-1.
(ii)当p≡5,11,17,23(mod 24)时,则G恰有8个互不同构的类型,即(i)中的G1、G2、G3、G4、G7、G8、G12、G16。
证明 (i)如果H平凡作用在群P上,那么容易得到G有4种互不同构的类型:G1、G2、G3、G4。 如果H非平凡作用在群P上,那么G=P∶H,即H/CH(P)同构于Aut(P)的一个非单位子群。设σ是模p的一个原根,则Aut(P)=σ是p-1阶循环群,所以H/CH(P)是一个不等于1的循环群。
1)当H≅H8时,为了使H/CH(P)成为非单位的循环群,只要CH(P)取为b、a2,b、a3,b、a,b2、a3,b2。 不难看出这5个群是互不同构的,所以由此可得G的5个互不同构的构造:G5、G6、G7、G8、G9。
2)当H≅H11时,CH(P)取为b、b,c、a,b,可使H/CH(P)分别为6,3,2阶循环群,从而得G的3个互不同构的构造:G10、G11、G12。
3)当H≅H13时,CH(P)只能取为b,c,使H/CH(P)是一个3阶循环群,从而得G的构造:G13。
4)当H≅H14时,CH(P)取为b,c、b,c,d、a,b,c可使H/CH(P)分别为6,3,2阶循环群,由此得G的3个不同构的构造:G14、G15、G16。
(ii)当p≡5,11,17,23(mod 24)时,H/CH(P)只可能是2阶循环群,因此这时G没有(i)中的构造G5、G6、G9、G10、G11、G13、G14、G15,从而G恰有8个互不同构的类型。
引理7 设p是奇素数,且p>3但p≠5或7。如果24p阶群G的Sylowp-子群P=x||x|=p的补子群H是非交换群:H9、H10、H12、H15,那么G恰有12个互不同构的类型:
G1=x×(a:b,c),其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1;
G2=x×(a:b),其中|x|=p,|a|=12,|b|=2,ab=a-1;
G3=x×(a:b,c),其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,ab=a,ac=b-1;
G4=x×(((b×c):a):d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,ad=a-1,bd=c,cd=b;
G5=(x×a):b,c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1,xb=x,xc=x-1;
G6=(x×a):b,c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1,xb=x-1,xc=x;
G7=(x×a):b,c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1,xb=x-1,xc=x-1;
G8=(x×a):b,其中|x|=p,|a|=12,|b|=2,ab=a-1,xb=x-1;
G9=x:(a:b),其中|x|=p,|a|=12,|b|=2,ab=a-1,xa=x-1,xb=x;
G10=x:(a:b,c),其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,ab=a,ac=b-1,xa=xb=x,xc=x-1;
G11=x:(a:b,c),其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,ab=a,ac=b-1,xa=xc=x,xb=x-1;
G12=x:(((b×c):a):d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,ad=a-1,bd=c,cd=b,xa=xb=xc=x,xd=x-1.
证明 如果H平凡作用在群P上,那么容易得到G有4种互不同构的类型:G1、G2、G3、G4。 如果H非平凡作用在群P上,那么G=P∶H,且H/CH(P)同构于Aut(P)的一个2阶循环群。
1)当H≅H9时,CH(P)可取为a,b、a,b2,c或a,b2,bc,从而可得G的3种构造:G5、G6、G7。 由于a,b≅C3:C4、a,b2,c≅C3×C2×C2、a,b2,bc≅(C3:C2)×C2,所以a,b、a,b2,c与a,b2,bc两两互不同构的,故G5、G6、G7是3个互不同构的24p阶群。
2)当H≅H10时,CH(P)取为a、a2,b、a2,ab,可使H/CH(P)为2阶循环群。令CH(P)=a或a2,b,分别得G的2个互不同构的构造:G8、G9。 若令CH(P)=a2,ab,则因为ab与b在H10中的地位是相同的,因而所得到的群G与G9同构。
3)当H≅H12时,CH(P)可为a,b或a,c。 又a,b和a,c是不同构的,因而得G的2个不同构的构造:G10、G11。
4)当H≅H15时,CH(P)只有取为a,b,c才能使H/CH(P)为2阶循环群,由此得G的构造:G12。
由引理4至引理7,易知定理1成立。
注:必须指出,文[7]中引理2遗漏了两种不同的类型,引理3的表述不对,证明过程是不严谨的;文[8]中引理2和3的证明存在错误。[7]中引理2的正确表述是:当Sylow 7-子群正规时,168阶群共有54种互不同构的类型(在本文的引理4至7中,令p=7即得);[7]中引理3的正确表述是:当Sylow 7-子群不正规时,168阶群只有3种互不同构的类型,其中仅有一种是不可解的,另外两种分别是Sylow 3-子群与Sylow 2-子群都正规时的1种和 Sylow 3-子群不正规而Sylow 2-子群正规时的1种(限于篇幅,我们在此不再详证此结论)。
