Analytical solution for Non-Darcian effect on transient confined-unconfined flow in a confined aquifer

Peng-yu Shi, Jian-jun Liu, Yi-jie Zong, Kai-qing Teng, Yu-ming Huang, Liang Xiao*

1 College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China.2 Guangxi Key Laboratory of Disaster Prevention and Engineering Safety, Guangxi University, Nanning 530004, China.3 Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education, Guangxi University, Nanning 530004, China.

Abstract: This paper presents a new analytical solution to investigate the mechanism of transient confinedunconfined flow in a confined aquifer induced by pumping with a large rate during mine drainage.The study focuses on understanding the impact of non-Darcian effect on flow towards a fully penetrated pumping well.The nonlinear relationship between specific discharge and the hydraulic gradient is described using Izbash's equation.A novel approximate method is developed to linearize the mathematical model, and the solution is derived using the Boltzmann transform.The proposed solution is validated by comparing it with previous works.The findings indicate that increased non-Darcian index, quasi-hydraulic conductivity,and specific storage have negatively affect the development of the unconfined region and aquifer drawdown, as greater turbulence flow accelerates recharge to the pumping well.Drawdown is found to be sensitive to the non-Darcian index, quasi-hydraulic conductivity, while it is unaffected by specific yield and specific storage.The conclusions provide valuable insights for mine drainage and the application of geological and hydrological conditions.

Keywords: Non-Darcian flow; Izbash equation; Boltzmann transform; Sensitivity analysis

Introduction

Coal resources account for 94.22% of total primary energy resources in China, leading to significant development in coal mining, particularly in deep coal mining.Deep coal mining operations are typically situated beneath confined aquifer systems and are prone to water inrushes, which have been proven one of the important factors affecting the mining safety (Xiao et al.2022; Zhao et al.2021).In order to prevent these water inrushes and ensure mining safety, mine drainage has proven to be a highly effective method for reducing hydraulic pressure in the confined aquifer.However, this drainage process can have detrimental effects on the groundwater resources within the mining area.Consequently, it is crucial to accurately assess the decline in water levels caused by drainage in the confined aquifer to safeguard mine safety and protect groundwater resources in the mining area.

The constant-rate pumping has been widely acknowledged an effective approach for drainage design (Moench et al.2001; Zong et al.2022).During the pumping process, if the pumping rate is sufficiently high or the duration of drainage is long enough, the hydraulic head in the confined aquifer can drop below the bottom of the overlying aquitard.This phenomenon leads to the development of a transient unconfined flow near the pumping well.Since 1970s, many analytical and numerical solutions have been proposed to investigate the flow mechanism associated with the transient conversion from confined to unconfined conditions.Moench and Prickett (1972) introduced the MP model and derived an analytical solution with the assumption that the aquifer transmissivity is constant.In the same vein, Elango and Swaminathan (1980) developed a numerical method to study the characteristics of the transient confinedunconfined flow within a confined region.Li et al.(2003) analyzed the mechanism of confined-unconfined flow using both analytical and numerical approaches in an initially dry aquifer.Hu and Chen(2008) presented an analytical solution based on Theis' equation.Wang et al.(2009) extended the MP model and Chen's model to develop a solution for transient conversion flow in a pumping well.Considering the variations in hydraulic properties(such as transmissivity, storativity and diffusivity)between confined and unconfined regions, Xiao et al.(2018) developed an analytical solution.They employed the Boltzmann transform under Darcian conditions.Subsequently, Xiao et al.(2022) utilized a semi-analytical method to investigate the delayed response of drawdown.

Based on a comprehensive literature review, it is noted that previous studies have predominantly assumed Darcian conditions for pumping-induced flow.However, fieldwork and actual experiments have provided evidences of non-Darcian flow occurring in a wide range of porous and fractured media surrounding pumping wells, regardless of the flow rate (e.g.Basak, 1976; Soni et al.1978;Sen, 1987, 1989, 1990; Bordier and Zimmer, 2000;Wu, 2001, 2002a, 2002b; Moutsopoulos and Tsihrintzis, 2005; Wen et al.2006, 2011; Houben, 2015;Feng and Wen, 2016; El-Hames, 2020; Jiong et al.2021; Hao et al.2021).In term of the non-Darcian flow induced by high pumping rates, two common functions are used to describe the nonlinear specific discharge: The Forchheimer equation and the Izbash's equation.The Forchheimer equation expresses the specific discharge as a second-order polynomial function of hydraulic gradient (e.g.Sen, 1987, 1990; Wu, 2002a; Moutsopoulos and Tsihrintzis, 2005; Mathias and Wen, 2015; Mathias and Moutsopoulos, 2016; Liu et al.2017),while the Izbash's equation describes the specific discharge as exponentially related to the hydraulic gradient.The Forchheimer equation considers viscous and inertial forces of water flow, and its polynomial form allows flexible representation of flow velocities, regardless of their magnitude (Wen et al.2008c; Moutsopoulos and Tsihrintzis, 2005).The Izbash's equation is suitable for modelling postlinear non-Darcian flow (Wen et al.2009; Chen et al.2003; Qian et al.2005), and can be more easily linearized in comparison with the Forchheimer equation.Over the past two decades, the validity of these two functions has been verified through their application in various types of aquifer hydraulic tests.These tests include slug test (Wang et al.2015; Ji and Koh, 2015), and pumping tests in different aquifer systems such as aquifer-aquitard system (Wen et al.2008a), fractured aquifers (Wen et al.2006), leaky aquifers (e.g.Wen et al.2011;Wen and Wang, 2013; Wang et al.2015), unconfined aquifers (Bordier and Zimmer, 2000; Mathias and Wen, 2015; Moutsopoulos, 2007, 2009),and confined aquifers (e.g.Wen et al.2008b,2008c, 2013).

The authors have observed that a high discharge rate during well pumping can cause a temporary transition from confined to an unconfined state in a confined aquifer (e.g.Chen et al.2006; Wang et al.2009; Mawlood and Mustafa, 2016; Xiao et al.2018, 2020, 2023).Additionally, it has also been reported that a large pumping rate can result in non-Darcian flow within the aquifer with a high Reynolds number (Rec＞10).Consequently, the drawdown in a confined aquifer induced by a high pumping rate is expected to be influenced by both the non-Darcian flow and transient confined-unconfined conversion.However, to date, there has been a lack of research on groundwater modelling on the transient confined-unconfined flow under non-Darcian conditions.

The paper presents an analytical solution for modelling the transient confined-unconfined flow under non-Darcian conditions.The flow in a confined region is described by a two-dimensional differential equation that represents the seepage system, while the flow in an unconfined region follows the Boussinesq equation with distinct hydraulic parameters.The boundary conditions in the conversion interface are expressed by the flow continuity.To capture the nonlinear relationship between specific discharge and hydraulic gradient,the Izbash's equation is employed for modelling purposes.The analytical solution is obtained by using the Boltzmann transform, which enables the development of a practical approach for assessing the dynamic development of the unconfined region in real-world scenarios.The time-drawdown curves are used to quantify the effect of the non-Darcian index and other hydraulic parameters, and a normalized sensitivity analysis is conducted to evaluate the response of drawdown to the different hydraulic parameters.

1 Model description and solutions

1.1 Conceptual-mathematical model

Fig.1 illustrates a schematic diagram of pumping test resulting from the transient confined-unconfined flow.The modelling assumptions are as follows: (1) The confined aquifer is isotropic and horizontal infinitely; (2) Both pumping and observation wells fully penetrate the confined aquifer;(3) The pumped rate,remains a constant over time; (4) The effective radius of the pumping well is considered infinitesimal.initial head of the confined aquifer, L.The governing equation can be expressed as (Wen et al.2008b, 2008c):

1.2 Linearization method

Using the Izbash's equation, the nonlinear specific discharge is depicted as:

Combining Equation (8) with Equation (6) yields:

2 Derivation of analytical solutions

In the section, the solution of the mathematical models for transient confined-unconfined flow is derived using the Boltzmann transform.As shown in Supporting Information, the analytical solution for the transient flow in the unconfined region is given by:

2.1 Drawdown simulation

Using Equations (12) and (13), we have developed an approach to simulate drawdown for transient

As shown in Fig.2, Hu and Chen (2008) considered that the total amount of groundwater drained to the pumping well is equal to the changes of groundwater storage of both the confined and unconfined regions.This can be expressed as:

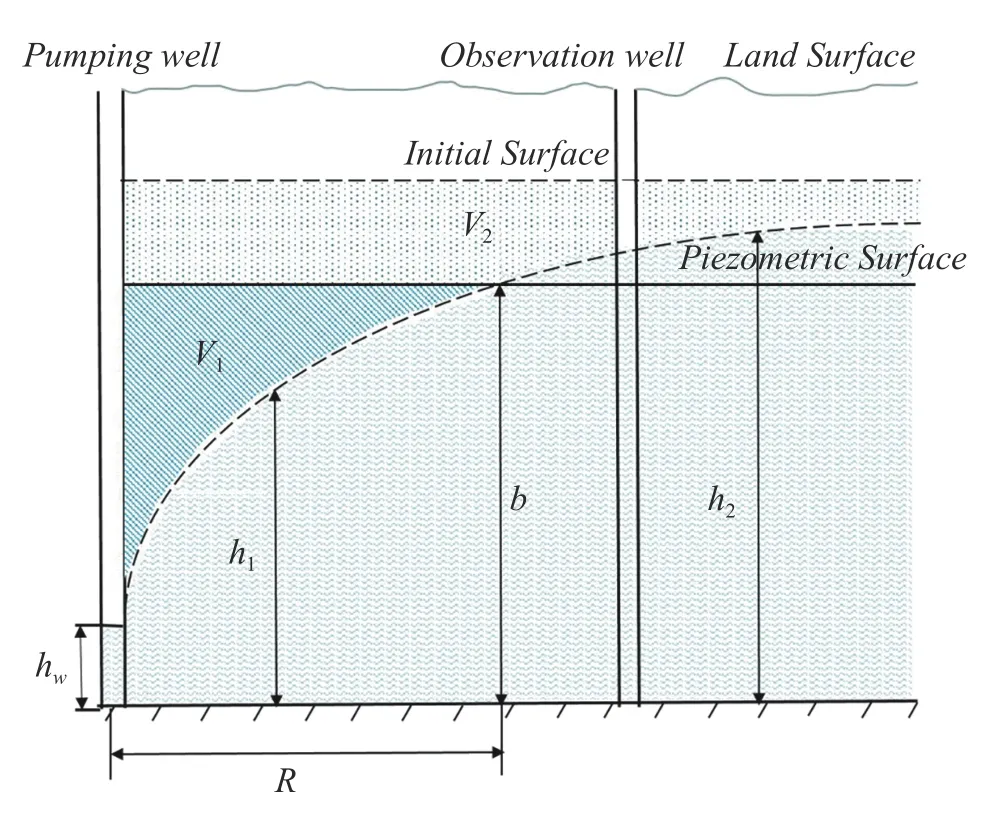
Fig.2 Change of groundwater storage during the confined-unconfined conversion (after Hu and Chen,2008)

Using Equations (14) and (16), the unknown values ofcan be simulated at each time point of interest.

2.2 Parameter estimations

The pumping test has been widely acknowledged as an effective method for assessing aquifer hydraulic parameters.By analyzing drawdown data obtained from fieldwork, an inversed analytical approach has been developed to determine the dynamic behavior of the unconfined region, as well as the diffusivity and specific yield of unconfined region under confined-unconfined conditions.This approach relies on the assumption that the parametersare known.

As shown in Fig.2, the unconfined region is radially expanded as pumping continues.The dynamic development of the unconfined region is typically characterized by the radial distance ()of the conversion interface from the pumping well.Letrepresent the water level (measured relative to the bottom of the confined aquifer) in the pumping well and the observation well,respectively.The radial distance between the pumping well and an observation well is denoted asThe transient confined-unconfined conversion flow occurs when the piezometric surface in the pumping well falls below the bottom of the overlying aquitard ().

During the early pumping stage, the piezometric surface is generally located above the top of the aquiferindicating that the flow towards the observation well is confined.In this case,can be determined by using Equation(13) as:

Considering the flow continuity and the Equation (4a), the expression at the transient interface can be obtained using Equation (13) as:

By combining Equations (17) and (18) and taking the ratio, it can be obtained:

Based on Equation (19), there are only two unknown parameters:.Therefore, given a specific time point of interest, we can calculate theR-value in the confined region by finding the root fined region can be estimated using Equations (17)and (18).of Equation (19).Once the-value is determined,the values of specific yieldof the uncon-

As the pumping continues, there comes a point where the water level in the observation well falls below the top of the confined aquifer＜b)after sufficiently long pumping time.In this scenario,can be calculated using Equation(12), which yields:

By using Equations (16), (18) and (20), the values ofR,Syandhmcan also be assessed for a given pumping time point.In summary, the steps to estimate the pumping test parameters are highlighted as follows: (a) Measure the water level in the observation well; (b) Ifb＜h′(r1,t) during the early time, employ Equations (17)-(19) to estimateR,Syandhmfor the confined region; ifh′(r1,t)＜b,use Equations (16), (18) and (20) to estimate theR,Syandhmfor the unconfined region.

3 Results and discussion

This section aims to evaluate the validity of the proposed solution by comparing it with the work conducted by Xiao et al.(2018).Additionally, the effects of hydraulic parameters, namelyn,Krand specific storage, on the drawdown andR-value simulation are examined.Considering the assumption that the flow exhibits non-Darcian behavior whenn＞1,a MATLAB program is employed to numerically simulate the drawdown at specific time of interest using the proposed solution.In general case, the hypothetical values of the parameters are given as within the following ranges:Kr, ranging from 0.0000011574 mns-nto0.00011574 mns-n(Wang, 2011);Sy, representing the specific yield of sand and fractured rock aquifers, ranging from 0.05 to 0.5; andS, ranging from 0.000001 to0.05(Marsily, 1986).

3.1 Reduction to flow under Darcian condition

Since the proposed analytical solution is intended for non-Darcian flow, it can also be employed to analyze Darcian flow under confined-unconfined conditions by considering a special case whenn=1.In this case, the proposed solution can be simplified to describe transient confined-unconfined flow under Darcian condition:

To verify the accuracy of the proposed solution,the results of drawdown simulation using the proposed solution whenn=1 are compared to those obtained by Xiao et al.(2018) through a hypotheticalcasestudy.Theparametervaluesused inthe comparisonareasfollows:Q=0.026 m3/s,Kr=0.0000695 m/s,S s=0.000002 m-1,Sy=0.3,b=30 m,h0=36 mandr1=10 m.Theconversionoccurs whenthedrawdownexceeds6 m.The simulated time-drawdown curves are presented in Fig.3.The results indicate that the proposed solution yields nearly identical outcomes to those of Xiao et al.(2018) during the early pumping period.However, slight differences between the two solutions are observed at later stage, likely attributed to the use of different linearization methods.The conversion time, approximately 0.1 day after the start of pumping, supports the acceptability of the proposed solution.

3.2 Effects of n constant on drawdown simulation

Fig.4 illustrates the drawdown curves obtained from a hypothetical study considering differentnconstants.The parametersused inthis studyareas follow:Q=0.04 m3/s,Kr=0.0000278m/s,S s=0.000002m-1,Sy=0.3,b=30 m,h0=36 m,r=10m,n=1,1.1, 1.2and 1.3.Inthiscontest, ahigher value ofnindicates a departure from Darcian flow,where groundwater is more easily transported within the aquifer, leading to a smaller drawdown at any given time of interest.Assuming that hydraulic head represents the hydraulic energy per unit weight of water (Wang et al.2015), an instantaneous decrease in water level within the well implies a loss of hydraulic energy.It is well-known in fluid mechanics that the turbulent flow (n＞1) is the most efficient in dissipating hydraulic energy compared to laminar and Darcian flow (Wang et al.2015).Consequently, a higher value ofncorresponds to a higher degree of turbulence flow(Wang et al.2015), suggesting greater recharge from the area farther away from the pumping well.As a result, a greaternvalue positively impacts the conversion time while negatively affecting the drawdown.In the case ofn=1.3, no confined-unconfined conversion occurs throughout the pumping duration, indicating purely confined flow.

Fig.3 Comparison of time-Drawdown curves with Xiao's model

3.3 Effects of Ss on R-Value and drawdown simulation

Fig.5 depicts theR-time curves of transient confined-unconfined flow under non-Darcian conditions.The curves are generated using the following parameters values:Q=0.04 m3/s,Kr=0.000003475 m/s,Sy=0.3,b=30m,h0=36m,r=10mandn=1.4for three differentS svalues of 0.0000016 m-1, 0.000002 m-1and0.0000025 m-1.It is important to note that a smaller specific storage results in a largerRvalue during the early stage.However, as the pumping continues, theRTime curves forthethree differentS svalues coincide with each other.

Fig.5 Time-R value curves for different S s value

The time-drawdown curves for the same hypothetical case but with different specific storages are compared in Fig.6.The differences between three drawdowncurves,correspondingtodifferentSsvalues,areprimarily observedduring theearly time period.Once the conversion occurs near the observation well, the drawdown curves align with each other,indicating thattheS svaluehas anegligible influence ondrawdownsimulation.Itcanbe attributed to the fact that, during the early time, the recharge primarily comes from the elastic storage of theaquifer.AlargerSsvalueimplies a greater release of waterfromtheaquifer, leading toa smaller drawdown at the initial stage.However,the seepage reaches a quasi-stable state towards the end of pumping, the effect of the elastic storage diminishes, exerting no significant impact on the drawdown andR-value of the transient confinedunconfined flow under non-Darcian conditions.

Furthermore, a decreasing slope is observed in the time-drawdown curve from the confined region to the unconfined region.This can be attributed to fact that, at the early pumping stage, the flow predominantly stems from the artesian storage ofS s.As the confined-unconfined conversion takes place, the release of artesian storage gradually decreases, while the discharge of gravity storage represented bySyis gradually increases.In practice,the specific yield is larger than the artesian storage,indicating a greater recharge to the pumping well and a slower decline of water level.

Fig.6 Time-Drawdown curves for different S s value

3.4 Effects of Kr constant on R-Value and drawdown simulation

Fig.7 shows the R-value and drawdown at various time points of interest for the hypothetical scenario ofQ=0.04 m3/s ,S s=0.000002 m-1,Sy=0.3,b=30 m,h0=36 m,r=10 m andn=1.4, considering three differentKrvalues: 0.00000278 m/s,0.00000348 m/s and 0.00000434 m/s.The findings reveal an inverse relationships between theRand drawdown values as theKrconstant varies.As the pumping continues, the amount of water released from the aquifer gradually decreases, and the recharge predominantly occurs from the regions located further away from the pumping well.With higherKrvalues, the flow is more easily transmitted within the aquifer, facilitating faster recharge from outer regions towards the pumped area.Consequently, the development of the unconfined region is constrained, leading to smaller drawdown and delayed conversion from confined flow to unconfined flow.

4 Sensitivity analysis

The objective of the sensitivity analysis is to assess the impact of different parameters on the hydrogeological model and streamline the parameter calibration process.Among the various methods available, local sensitivity analysis has been selected as the calculation approach to evaluate the influence of individual parameters on the analytical solution.In this case, the hydraulic parameters are assumed to be independent of each other.In comparison with Theis' solution, the modeling for transient confined-unconfined flow under non-Darcian conditions involves four key parameters:Quasi-hydraulicconductivityKr,non-Darcianindexn,specificyieldSy, and specificstorageS s.Therefore, conducting a sensitivity analysis becomes necessary.

The sensitivity is defined as a rate of change in one factor with respect to a change in another factor.Based on the work by Huang and Yeh(2007), the normalized sensitivity parameter is defined as:

Where: ΔPjis a small increment usually set as 10-2×Pj.Fig.8 illustrates the normalized sensitivity ofS s,Sy,Kr, andn, withQ=0.04 m3/s,S s=0.000002 m-1,Sy=0.3,b=30 m,h0=36 m,r=10 m,n=1.4 andKr=0.00000348 m/s.

Fig.8 Sensitivity analysis of aquifer parameters

Fig.8 displays the temporal variation of normalized sensitivity with respect toSs,Sy,Krandnvalues.It is worth noting that the normalized sensitivity ofS s,Sy,Krandngenerally exhibits negative values, indicating a negative relationship.In other word, an increase inS s,Sy,Krandncan lead to a decrease in drawdown at the observation well.The normalized sensitivity coefficient curves ofKrandndemonstrate convex shapes, coinciding with the occurrence of conversion from transient confined flow to unconfined flow after approximately 75 hours of pumping.This corresponds to the time when the normalized sensitivity reaches its peak value.This suggests that the normalized sensitivity in the confined region initially decreases with time, but then increases after the confinedunconfined conversion takes place.

5 Conclusions

Greater values ofnandKrresult in increased turbulence in flow, which negatively affects the development of the unconfined region and the drawdown of the aquifer.However these values have a positive effect on the time it takes for the conversion from confined to unconfined flow.

A larger specific storage implies a greater release of water from the elastic storage of the aquifer.This initially has a negative impact on the drawdown and the development of the unconfined region during the early stage of pumping.However, as pumping continues, these effects diminish.

The drawdown is particularly sensitive to the power indexnand quasi-hydraulic conductivityKr.The normalized sensitivity ofnandKrin the confined region initially decreases with time, but then increases after the confined-unconfined conversion occurs.On the other hand, the drawdown is not significantly affected by both the specific storage (S s) and specific yield (Sy).Nomenclature

Q-constant pumping rate, L3T-1;

q-specific discharge, LT-1;

Kr-quasi-hydraulic conductivity of the aquifer LnT-n;

S-storativity coefficient;

Sy-specific yield of the unconfined region;

S s-specific storage, L-1;

b-the thickness of the confined aquifer, L;

h0-initial head, L;

h1(r,t) -elevation of piezometric surface in unconfined region, L;

h2(r,t) -elevation of piezometric surface in confined region, L;

hm(r,t) -effective elevation of piezometric surface within the range from b to zero in the unconfined region, L;

h′(r,t) -elevation of piezometric surface in an observation well, L;

r-radial distance, L;

r1-distance of observation well from pumping well, L;

R- radial distance of conversion interface from pumping well, L;

n-power index, an empirical constant in the Izbash's equation;

t- the pumping time, T;

W(u) -theis well function.

Acknowledgements

This study was supported by the national natural science foundation of China (Grant Numbers 41807197, 2017YFC0405900, and 51469002), the natural science foundation of Guangxi (Grant Numbers 2017GXNSFBA198087, 2018GXNSFAA 138042, and GuiKeAB17195073), and Hebei high level talent funding project (B2018003016).