二维磁性半导体笼目晶格Nb3Cl8单层的磁性及自旋电子输运性质*
2024-01-06樊晓筝李怡莲吴怡陈俊彩徐国亮安义鹏
樊晓筝 李怡莲 吴怡 陈俊彩 徐国亮 安义鹏
(河南师范大学物理学院,新乡 453007)
1 引言
随着石墨烯的制备及其优异性能的发现,二维(2D)材料受到人们的广泛关注[1,2].许多二维材料被预测并通过实验合成,包括过渡金属二硫族化物[3-7]、过渡金属二卤族化物[8]、硼烯[9-14]、磷烯[15-18]、MnBi2Te4[19]、MA2Z4家族[20-22]等材料.它们诱人的应用前景及其新颖的物理和化学性质,为设计和制备新型材料和器件的实验工作提供了不竭的动力.研究发现,二维半导体材料可以表现出许多功能特性,例如整流效应[23]、场效应行为[24-26]、自旋过滤效应[19,27]等,可以作为整流器、场效应晶体管和自旋开关等的重要候选材料.随着量子计算的飞速发展,对低功耗、小尺寸和高效率的自旋电子学器件提出了更高的要求.如何实现电荷与自旋的交互控制成为目前的研究热点[28-31].实现半导体中的自旋性质主要有两种途径: 一种是制备具有高居里温度的磁性半导体;另外一种方式是利用二维铁磁金属或二维半导体异质结来实现半导体中的自旋注入.例如,通过搭建二维铁磁金属Fe3GaTe2同质结[32];Fe3GaTe2与半导体的异质结[33];基于Fe3GeTe2二维铁磁电极,利用InSe[34],GaSe[35],Cr2Ge2Te6[36]等作为中间层,实现高效的室温自旋注入.另外,研究者曾尝试通过引入缺陷[37]和掺杂磁性元素[38]等方法诱导二维材料产生磁性相变.但在实验中很难有效控制杂质和缺陷的分布以获得稳定的磁性.2017年至今,Cr2Ge2Te6[1],CrI3[39],CrBr3[40]和CrCl3[41]等二维本征磁性半导体材料被先后报道,使得自旋电子学器件得到了进一步的发展.
近年来,笼目晶格结构因其独特的磁性[42,43]和电学性质[44]引起了人们极大的研究兴趣.笼目晶格是由共角三角形围成的六边形结构,这种特殊的晶格结构导致材料中通常存在狄拉克点、平带和范霍夫奇点[45-49].在包含自旋-轨道耦合和磁性的情况下,该晶格结构可以表现出多种非平庸的拓扑电子或磁性态[49,50],如Weyl费米子、量子化反常霍尔态等.之前发现的笼目材料大多是没有带隙的金属,这明显限制了它们在半导体器件方面的应用.最近,一种新的具有笼目晶格结构的二维磁性半导体材料Nb3Cl8单层被成功制备出来[51],通过角分辨光电子能谱和第一性原理计算证实了半导体基态和拓扑平带的存在,其对可见光和紫外光具有较强的响应[52].尽管Nb3Cl8单层具有优异的性能,但相关磁性和输运性质尚未开展深入研究.
本文通过第一性原理方法系统地研究了Nb3Cl8单层的磁性,探究了其磁各向异性,及应力应变对其磁性的量子调控,设计了基于Nb3Cl8单层的p-n结二极管原型纳米器件,并采用密度泛函理论结合非平衡格林函数方法计算了其自旋极化的电子输运性质,揭示了其器件功能特性及在下一代高性能自旋电子学器件领域的潜在应用.
2 计算方法
二维Nb3Cl8单层的电子结构、磁各向异性和输运性质结果通过密度泛函理论(DFT)[53]结合非平衡格林函数(NEGF)[54,55]方法确定,在Quantum ATK程序包代码中运算获得[56].计算过程中使用PseudoDojo模守恒赝势[57]、原子轨道线性组合基组以及自旋极化广义梯度近似交换关联泛函[58].为了避免相邻层之间的相互作用,真空层厚度设为25 Å.采用55 Hatree的实空间网格密度截断能求解泊松方程.在结构优化中,收敛标准为总能量容差小于 10-6eV,每个原子受力小于 10-2eV/Å.对Nb3Cl8单层Z型p-n结二极管纳米器件左右电极的布里渊区采样时,设置了3×1×150的Monkhorst-Packk点网格[59].
3 计算结果和讨论
3.1 Nb3Cl8单层的原子结构和电子特性
图1(a)为Nb3Cl8单层的俯视图和侧视图.Nb3Cl8单层的空间群为P3m1 (No.156),具有三聚笼目晶格结构,其中三个Nb原子形成一个三角形团簇,每个单胞包含3个Nb原子,8个Cl原子.考虑铁磁基态[52],计算所得Nb3Cl8单层晶体的晶格参数为6.817 Å,与Jiang等[52]用DFT+U方法预测的相应值6.744 Å,和Mortazavi等[60]用广义梯度近似方法预测的6.783 Å相当接近.计算得到的总磁矩M=0.997 μB,与通过密度泛函理论高通量预测[61]的M=1 μB一致.
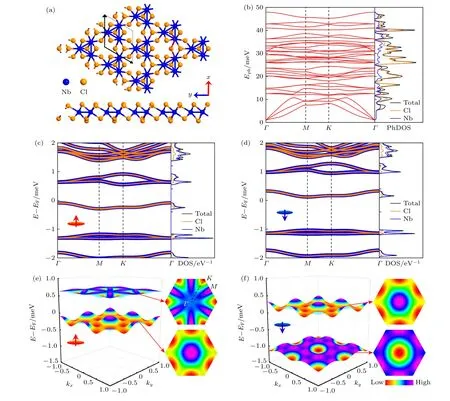
图1 (a) Nb3Cl8单层晶体结构的俯视图(上)和侧视图(下),x轴代表锯齿型方向;(b) 声子谱以及投影声子态密度;自旋向上(c)和向下(d)状态的元素投影电子能带以及投影态密度;Γ点附近自旋向上(e)和向下(f)状态的导带与价带的三维视图以及在第一布里渊区的二维投影;色卡显示了图(e)、图(f)中从低(红色)到高(紫色)的能量本征值;费米能级(EF)设置在能量零点位置Fig.1.(a) Top view (top) and side view (bottom) of Nb3Cl8 monolayer crystal structure,x axis refers to the zigzag irection;(b) phonon spectrum and phonon projected density of states;element-projected electronic band and density of states for the spin-up(c) and spin-down (d) states;3D views for the spin-up (e) and spin-down (f) states of the conduction and valence bands around the Γ point,and 2D views in the first Brillouin zone projection.Color map shows the values for (e),(f) from low (red) to high (purple).the Fermi level (EF) is set at the energy zero position.
如图1(b)所示,Nb3Cl8单层的声子谱在整个布里渊区中没有虚频,证明结构是动力学稳定的,在没有衬底的情况下可以保持独立的稳定结构.由于Nb3Cl8单层的每个单胞含有11个原子,共有33条声子分支,包含3条声学(A)支和30条光学(O)支,在低频声学支部分Nb原子和Cl原子贡献相当,对高频光学支Cl原子的振动起主要贡献.进一步使用以下公式计算了其形成能Ef=-2.014eV,证明了Nb3Cl8单层结构的稳定性.
其中Ef为形成能;Etot为Nb3Cl8单层的总能量,E(Nb)和E(Cl) 分别为Nb元素单质和Cl元素单质的能量.图1(c)和图1(d)分别为自旋向上态和自旋向下态的元素投影电子能带及态密度.Nb3Cl8单层自旋向上态的导带最小值和价带最大值分别出现在K点和Γ点,而自旋向下态的导带最小值和价带最大值均位于M点.两种自旋态在费米能级附近的电子态都主要由Nb原子的d轨道贡献,自旋向下态的带隙(1.157 eV)明显大于自旋向上态的带隙(0.639 eV).此外,考虑自旋-轨道耦合效应时其能带结构劈裂与自旋极化的能带结构吻合较好,见补充材料图S1 (online).这些结果表明,费米能级附近的导带和价带具有自旋极化效应,该材料可作为自旋电子器件的候选材料.
为了更深入地了解费米能级(EF)附近的电子态,在三维视图和第一布里渊区投影中研究了Nb3Cl8单层Γ点附近的导带及价带的能量色散关系.如图1(e)和图1(f)所示,锥形(漏斗形)带在高对称性点处形成坚固的六边形结构,Γ点附近的能量色散和有效质量基本呈现各向同性,远离Γ点处,能量色散和有效质量各向异性增强.自旋向下态价带顶部沿x轴方向的空穴有效质量(-5.284me)大于其导带底的电子有效质量(2.059me)及自旋向上态价带顶部的空穴有效质量(-2.870me)和导带底的电子有效质量(2.203me).对于载流子而言,较大的有效质量导致其与晶格的耦合较强,对应能量色散关系较弱,使得载流子输运能力降低.据此,可以初步推断出自旋向上态的输运能力应强于自旋向下态.
磁各向异性(EMA)是二维磁性材料自旋电子学应用的重要参数,主要来源于自旋-轨道耦合效应[62],根据晶格结构定义了特定方向上磁化强度的稳定性.使用力场原理[63]来研究Nb3Cl8单层的EMA,其中能量差异由自旋-轨道耦合的非自洽能带能量计算得到:
其中θ0,φ0为所在平面内零参考处的极角;θ1,φ1为所在平面 内的其他极角;fi(θ,φ) 为自旋取向(θ,φ) 的能带i的占据因子;εi(θ,ϕ) 为对应的能带能量.Nb3Cl8单层的角依赖性和轨道投影EMA计算结果如图2所示.
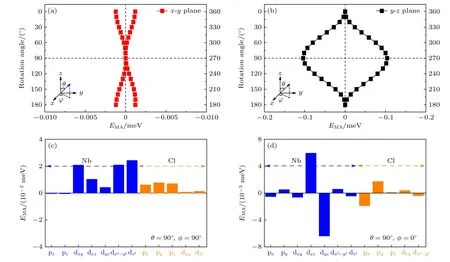
图2 (a) x-y平面内EMA随极角θ和φ的变化;(b) y-z平面内EMA随极角θ和φ的变化,插图显示极坐标;(c) θ=90°,φ=90°(y轴方向)的EMA轨道投影;(d) θ=90°,φ=0°(x轴方向)的EMA轨道投影;y轴(θ=90°,φ=90°)和z轴(θ=0°,φ=90°)方向的能量设置为x-y和y-z平面的零参考Fig.2.(a) EMA variation with polar angles θ and φ in the x-y plane;(b) EMA variation with polar angles θ and φ in the y-z plane,inset shows polar coordinates;orbital projections of EMA corresponding to polar angles of (c) θ=90°,φ=90° (y axis direction) and(d) θ=90°,φ=0° (x axis direction).Energy of y axis (θ=90°,φ=90°) and z axis (θ=0°,φ=90°) directions are set as zero reference of the x-y and y-z plane.
结果表明,面内和面外(分别对应于x-y和y-z平面)的能量都是各向异性的.图2(b)表明,y-z平面内当θ=90°时各向异性最弱.同样地,如图2(a)所示,保持θ=90°即在x-y平面内φ=0°对应的EMA略低于其他角度,这表明Nb3Cl8单层的易磁化轴在平面内并且沿x轴方向.此外,对应极角为(θ=90°,φ=90°)和(θ=90°,φ=0°) 的EMA轨道投影结果如图2(c)和图2(d)所示.Nb原子的dz2,dxz和轨道对 (θ=90°,φ=90°) 极角处的EMA起主要作用,dxz和dyz轨道主要对(θ=90°,φ=0°)极角处的EMA起作用.
3.2 应变对Nb3Cl8单层磁性的影响
应变诱导的磁性相变已经在许多材料中得到证实[64-66],本文尝试通过施加应力应变探究Nb3Cl8单层的性质变化.施加应力应变的定义为ε=(aa0)/a0,其中a0为Nb3Cl8单层原始的晶格常数,a为施加应变后Nb3Cl8单层的晶格常数.对结构施加了0%至-6%的压缩应变和0%至6%的拉伸应变,图3(a)显示,施加应变时,自旋向下态的带隙减小,而自旋向上态的带隙从负(压缩)应变到正(拉伸)应变单调递减.ΔE是Nb3Cl8单层总能量随应变的变化量,定义为 ΔE=E1-E0,其中E0为体系在未施加应变时的总能量,E1为施加应变后的能量.从图3(b)可以发现,在施加应变时,Nb3Cl8单层的总能量随应变的增大而逐渐升高,然而其总磁矩几乎保持不变,表明其磁性在有限应变下的高度稳定性.另外发现,从-6%—6%的应变下,金属Nb原子对总磁矩的贡献逐渐增大.Nb3Cl8单层的易磁化轴在-6%应变下处于面内,沿y轴方向;自由状态下(即0%应变)易磁化轴在平面内,沿x轴方向;6%应变下指向面外,沿z轴方向(见补充材料图S2 online).结果表明应变可使Nb3Cl8单层的易磁化轴发生面内-垂直方向的翻转,有望通过应力应变调控Nb3Cl8单层的磁性.
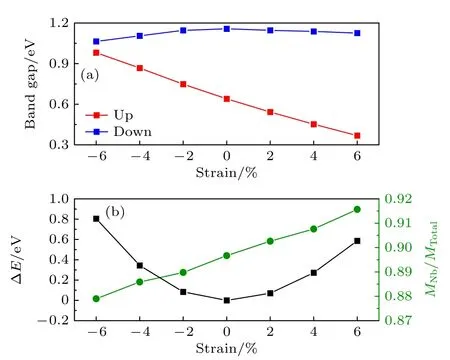
图3 (a) Nb3Cl8单层自旋向上态与自旋向下态带隙随应力应变的变化;(b) Nb3Cl8单层能量变化量(ΔE)和Nb原子对总磁矩的贡献(MNb/MTotal)随应力应变的变化Fig.3.(a) Variation of the band gap with strain in the spin-up and spin-down states of Nb3Cl8 monolayer;(b) variation of the energy change (ΔE) and the contribution of Nb atoms to the total magnetic moment (MNb/MTotal)with strain in the Nb3Cl8 monolayer.
3.3 Nb3Cl8单层p-n结二极管的输运性质
为了解 Nb3Cl8单层的电子输运性质,采用p型和n型原子补偿电荷的静电掺杂方法[67]构造了基于Nb3Cl8单层的p-n结二极管(图4(a)),锯齿型(zigzag)方向作为输运方向.本文中,对样品进行了3×1012cm-2浓度的掺杂 (对应于常见的1019cm-3的体掺杂浓度)[67-69].Nb3Cl8单层的p-n结二极管由漏极(D)和源极(S)以及中心散射区(p-n结)组成.D和S电极由p/n型掺杂的Nb3Cl8超胞描述,其长度沿传输方向半无限延伸.当施加正向D-S偏压Vb时,会产生正电流,从D电极流向S电极,反之亦然[27].通过Nb3Cl8单层p-n结二极管的电流I由Landauer-Büttiker公式[70]确定:
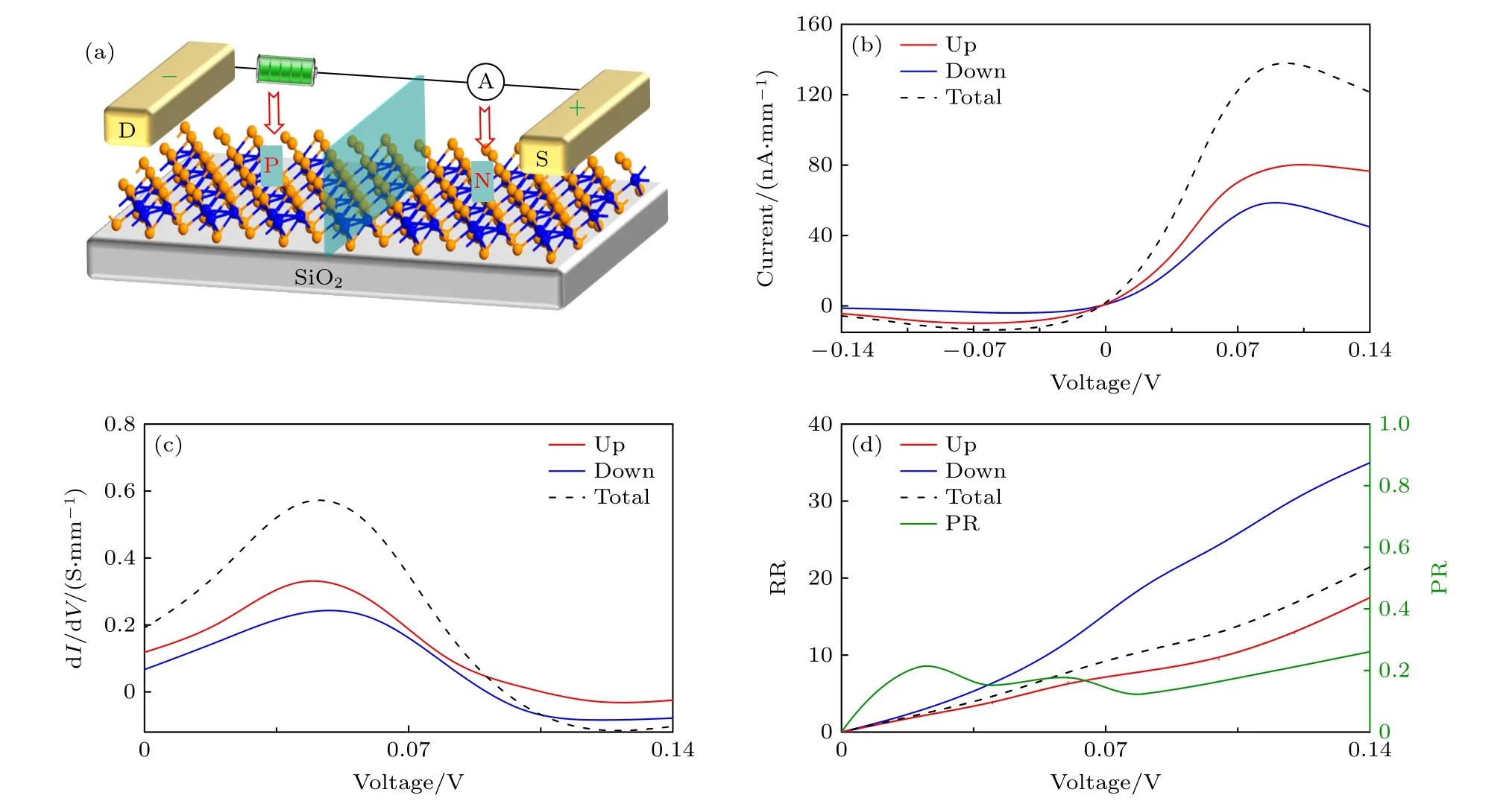
图4 (a) Z型Nb3Cl8单层p-n结二极管示意图;(b) Z型Nb3Cl8单层p-n结二极管I-V曲线;(c) Z型Nb3Cl8单层p-n结二极管的微分电导(dI/dV)曲线;(d) Z型Nb3Cl8单层p-n结二极管整流比(RR)和极化比(PR)Fig.4.(a) Schematic diagram of Z-type Nb3Cl8 monolayer p-n junction diode;(b) I-V curve of Z-type Nb3Cl8 monolayer p-n junction diode;(c) differential conductance (dI/dV) curve of Z-type Nb3Cl8 monolayer p-n junction diode;(d) rectification ratio (RR)and polarization ratio (PR) of Z-type Nb3Cl8 monolayer p-n junction diode.
式中σ是自旋指数;e代表电子电荷;h为普朗克常数;Tσ(E,Vb)是指p-n结的自旋透射系数;fD(S)=是D(S)电极的费米-狄拉克分布函数,其中µD(S)代表化学势,TD(S)指电子温度.本文偏置电压范围Vb为 -0.14 —0.14 V,采样间隔为0.02 V.
图4(b)中Z型Nb3Cl8单层p-n结二极管电子输运的电流-电压(I-V)曲线显示出明显的整流效应,即电流在有限的负向偏置电压下被禁止(电路关闭状态),而在施加正向偏置电压时打开(电路开启状态).Nb3Cl8单层p-n结二极管的整流比定义为 RR=|I(Vb)/I(-Vb)|,整流比曲线见图4(d).此外,在I-V曲线中观测到显著的负微分电阻现象.最初电流随着偏置电压的增加而线性增加,直到在0.08 V或0.1 V达到峰值,当电压进一步升高时,电流开始存在下降趋势.电流极化比定义为PR=(I↑-I↓)/(I↑+I↓),Nb3Cl8单层p-n结二极管在正偏压下具有0.26的极化比(图4(d)).这些结果表明,自旋向上态的电流大于自旋向下态的电流,Z型Nb3Cl8单层p-n结二极管表现出自旋过滤效应.值得注意的是,掺杂浓度的提高会增加电流密度,但会一定程度上降低自旋极化率[19],在实验实现上高浓度掺杂的难度也会增加.
4 结论
本文通过密度泛函理论结合非平衡格林函数方法研究了Nb3Cl8单层的电子结构、磁各向异性以及p-n结二极管的自旋输运性质.结果表明,Nb3Cl8单层的磁矩为0.997 μB,易磁化轴在平面内并且沿x轴方向,Nb 原子对磁各向异性作主要贡献.压缩应变和拉伸应变都会减小自旋向下态的带隙,自旋向上态的带隙与晶格常数的变化成反比.从-6%到6%的应变下,Nb原子对总磁矩的贡献增大,Nb3Cl8单层的易磁化轴发生面内-垂直方向的翻转.此外,基于Nb3Cl8单层的p-n结二极管具有整流效应,自旋向上态的电流大于自旋向下态的电流,表现出自旋过滤效应和负微分电阻现象.这些结果揭示了Nb3Cl8单层材料在高性能自旋电子器件中的潜在应用,为该材料和相关二维材料进一步的实验验证和探索提供了指导.
感谢河南师范大学高性能计算中心.
