基于频率比模型和随机森林模型耦合的地质灾害易发性评价

翟文华,王小东,吴明堂,吴晓亮,李倩倩

(1. 华北水利水电大学 地球科学与工程学院,河南 郑州 450000; 2. 中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310000)

0 引言

中国是一个地质灾害多发的国家,依据自然资源部发布的数据,2021年全国发生地质灾害4772起,造成大量的人员伤亡和经济损失。而在我国南部地区由于受雨水浸泡、河流冲刷和人类工程活动的影响,多数山区城镇面临滑坡、崩塌此类地质灾害的威胁,需进行区域性地质灾害易发性评价。地质灾害易发性评价[1]是区域预警评价前期重要的准备工作,主要研究在一定空间下由于环境因素导致地质灾害发生概率的大小,其对区域防灾减灾有着重要意义。

目前地质灾害易发性评价模型众多,以知识驱动模型和数据驱动模型为主[2]。知识驱动模型以专家经验为主,评估过程简单,容易理解,但其主观性过强,导致评价结果无法进行对比分析[3],常用的知识驱动模型有模糊逻辑[4]、层次分析[5-6]和专家打分法[7]。数据驱动以机器学习为主,能够高效地解决地质灾害与环境因子间复杂的非线性关系,常用的数据驱动模型有支持向量机[8-9]、逻辑回归[10]、随机森林[11]和神经网络[12]等。如黄发明等[13]将聚类分析与支持向量机相结合运用到重庆市地质灾害多发区段的万州区进行滑坡易发性评价,结果表明聚类分析-支持向量机模型比支持向量机模型具有更好的预测效果。何书等[11]将自组织特征映射网络模型和随机森林模型结合对江西省赣州市西南部地区进行了滑坡易发性评价模型,结果显示自组织特征映射网络与随机森林相结合的模型比随机森林模型具有更高的预测精度。黄立鑫等[12]将径向基函数神经网络模型与信息量模型进行耦合,进而对甘肃省岷县进行滑坡灾害易发性评价,结果表明径向基函数神经网络与信息量耦合模型比单一的神经网络及信息量模型具有更好的评价精度。综上所述,数据驱动模型在地质灾害易发性评价领域具有广泛的应用。为了对模型进行有效训练和测试,需选取与已知地质灾害单元量相匹配的非地质灾害单元量,而非地质灾害单元的选取目前只是主观推测或随机选取,可能导致选取的非灾害单元位于地质灾害单元附近的潜在地质灾害单元之上[14],并不能保证所选的非地质灾害单元具有较低的易发性。为减少此类情况的发生,提高地质灾害单元与非地质灾害单元的辨识度,采用从频率比模型结果中选取非地质灾害单元。在此基础上,构建频率比支持下的随机森林模型进行地质灾害易发性评价。

近年来,浙江省长兴县李家巷地区经济快速发展,工程活动不断加剧,造成该地区地质环境不断恶化,多地区发生滑坡、崩塌,对当地居民的生命及财产造成了威胁。因此,本文以李家巷为研究区,利用频率比-随机森林模型对李家巷进行地质灾害易发性评价,随后将频率比-随机森林模型与随机森林模型进行比较,探讨本文提出方法的可行性。

1 研究区概况及数据源

1.1 研究区概况

李家巷镇位于浙江省长兴县,总面积约53.13km2,地势总体西低东高如图1所示,研究区内水系众多,多年平均气温为23℃,多年平均降水量达1701 mm,属亚热带季风气候。地层岩性主要以砂岩、碎屑岩、砾岩和碳酸盐岩为主。近年来,李家巷人类工程活动加剧,如城市建设、矿产开采等,都会对环境造成一定程度的危害,进而引发地质灾害的发生。以上复杂的环境条件,共同孕育了李家巷地区频发的地质灾害。研究区典型的地质灾害有第二石矿矿区南侧滑坡如图2所示。

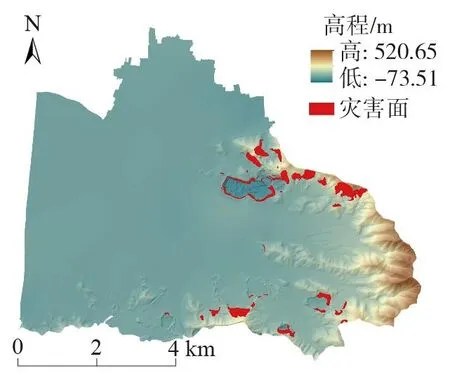
图1 研究区位置Fig. 1 Location of the study area

图2 研究区滑坡现场照片Fig. 2 Photo of landslide site in the study area

1.2 数据源

本研究采用的数据源于历史地质灾害数据库、全球地表覆盖数据库、地理空间数据云平台、李家巷地质灾害风险评价报告,主要包括:LandsatTM8影像1景(2019-05-23,轨道号119/038),用于获取归一化植被指数(normalized difference vegetation index, NDVI); 数字高程模型(digital elevation model, DEM)数据用于提取坡向、坡度和曲率等信息;通过1∶50000地质图提取断层,岩组等信息;地质灾害编录数据和野外调查资料等。研究区地质灾害分布的总面积达975209 m2,本文采用10 m×10 m的栅格,研究区共划分为156051个地质单元栅格。

2 评价方法

2.1 频率比计算

易发性评价的基础是对某一环境指标因子进行分类并计算各分类状态对灾害的影响程度,常采用频率比[15]来实现该过程以提高分类的准确性。频率比(frequency ratio, FR)可以归纳为某因子分类区间内灾害栅格数占所有灾害栅格百分比与该分类区间栅格数占研究区总栅格数百分比的比值。计算公式为:

(1)

式中:Fj为某因子在分类区间内出现地质灾害的栅格数;F为区间内所有地质灾害栅格总数;Cj为某因子在分类区间内的栅格数;C为研究区栅格总数。

FR表明了评价因子各分类区间对于地质灾害发生的影响程度:FR>1表明该评价因子分类区间对地质灾害的发生具有较强的影响。FR≤1说明该评价因子分类区间对灾害发生影响不大。

2.2 随机森林模型

为了弥补单棵决策树的不足,本文采用随机森林(random forest, RF)算法。随机森林是一种新型集成分类器[16]。使用Bootstrap重采样技术,从样本集T中有放回地随机抽取n个样本(占总样本的2/3)作为训练样本集,每条训练样本数据用于训练一棵树,共生成n个树组成的森林,预测数据时需根据n棵树的结果,取众数或平均值作为结果,流程如图3所示。随机森林参数的选择将会直接干扰模型泛化能力和预测效果,本文利用网格搜索算法确定模型的基本参数(森林中的树木数量、树的最大深度、特征数量等)。

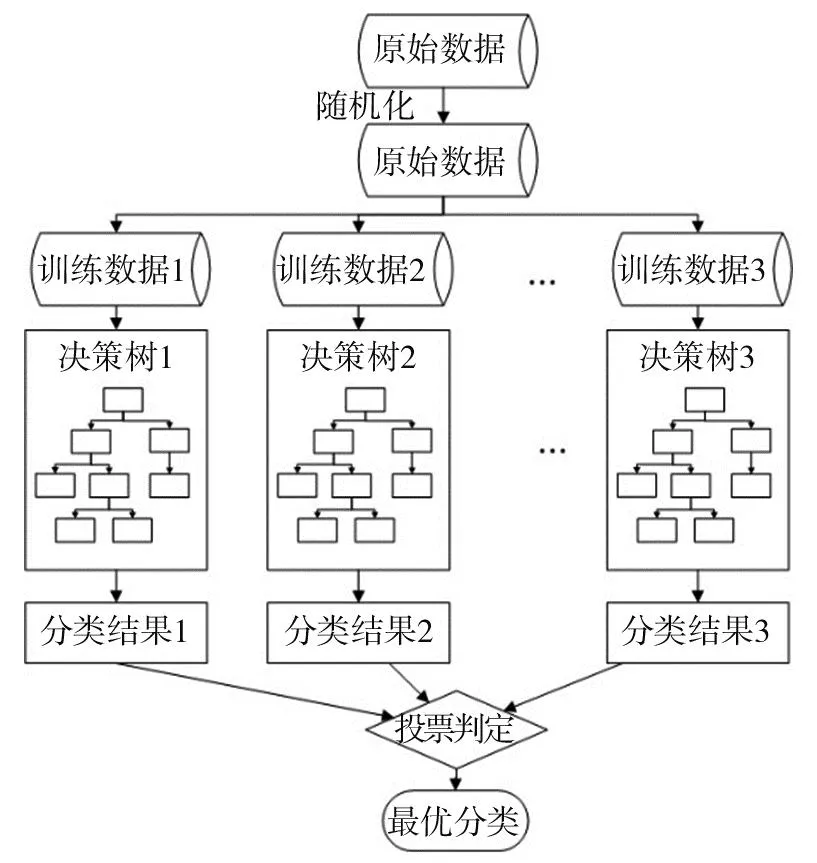
图3 随机森林算法流程Fig. 3 Flow of random forest algorithm

2.3 频率比-随机森林模型构建流程

频率比-随机森林(FR-RF)模型主要包含4步:①对评价因子进行相关性分析及利用频率比计算各评价因子对地质灾害的影响程度;②根据频率比模型结果进行非地质灾害单元的选取;③将地质灾害单元、选取的非地质灾害单元和评价因子输入到的RF模型中,进行易发性评价计算;④对RF模型和FR-RF模型进行评估和对比分析,具体流程如图4所示。

图4 频率比-随机森林模型流程Fig. 4 Frequency ratio-random forest model process

3 评价指标体系建立

评价因子的选取和评价单元的确定是进行灾害易发性评价的重要前提条件。地质灾害的发生不仅由环境因素引起还与人类活动有关,在结合相关文献[1-13]中相似地区的地质条件、灾害发育特征及形成背景的基础上,从本文1.2节数据源中获取评价指标,并进行相关性分析(表1)以确保环境因子之间具有较弱的相关性。最终选取9个环境因子:高程(DEM)、坡度、坡向、岩组、剖面曲率、距离断层的距离、距离水系的距离、土地利用和归一化植被指数(NDVI),如图5所示。地质灾害易发性评价的基本评价单元主要包含栅格单元、斜坡单元、行政区划单元等[17-18],栅格单元具有结构简单、方便计算等优势,因此本文以栅格作为基本评估单元。

表1 评价因子间的相关系数Table 1 Correlation coefficients among evaluation factors

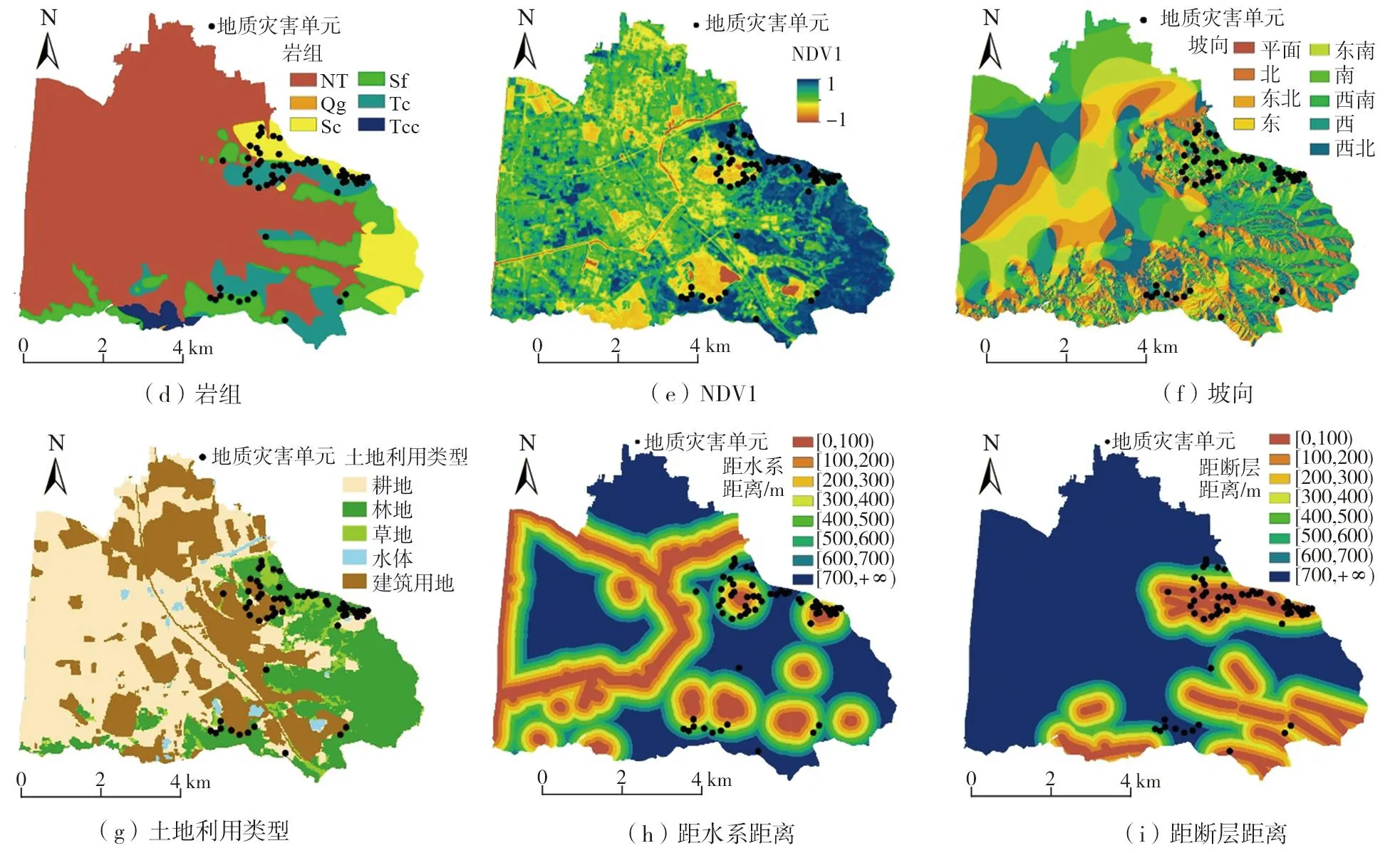
图5 评价因子专题图Fig. 5 Evaluation factors

这些数据包含连续型因子和离散型因子,结合各因子分布规律利用等间隔或自然断点法进行划分,划分结果如表2所示。其中岩组中NT为以黏性土为主的岩组,Qg为坚硬块状以花岗岩为主的酸性岩岩组,Sc为坚硬较坚硬以砂岩、砾岩为主的粗碎屑岩岩组,Sf为软硬不均较坚硬中层以粉砂岩、泥岩为主的细碎屑岩岩组,Tc为坚硬中至厚层状以碳酸盐岩为主的岩组,Tcc为较坚硬薄至中层状以碳酸盐岩、碎屑岩为主的岩组。本文使用频率比计算环境因子的各分类区间对地质灾害发生的影响程度。由表2可知,高程在17～302 m范围内、坡度大于10°的坡面、坡向为北、南和西南、NDVI在0.0～0.23和大于0.51、断层距离小于600 m、水系距离小于700 m、土地利用类型为草地林地以及岩组为Sc,Sf和Tc分别在各所属因子里面占据较高的频率比值,易导致地质灾害的发生。

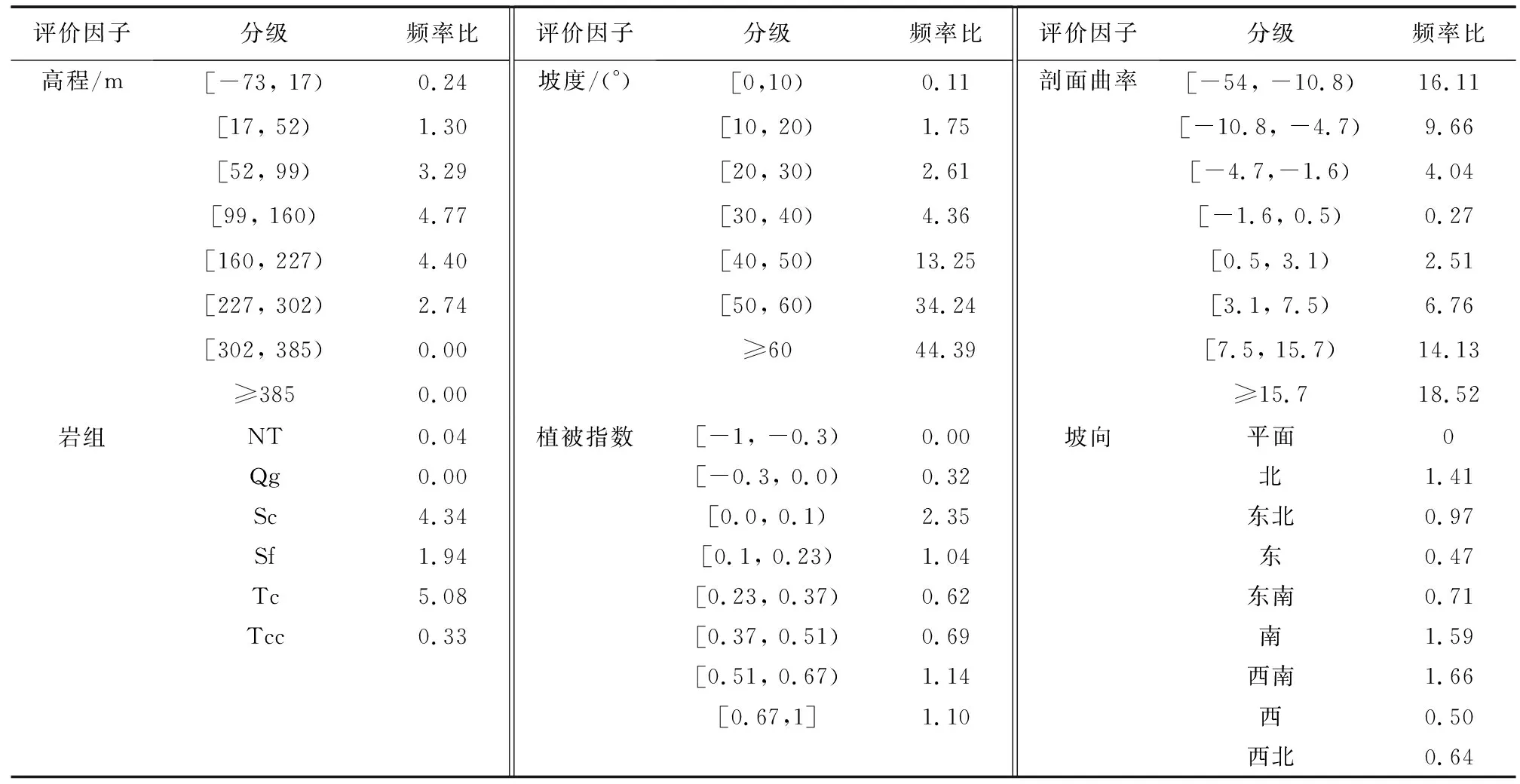
表2 各评价因子频率比值Table 2 Frequency ratio of each evaluation factor

4 灾害易发性评价

4.1 频率比模型

利用FR对环境因子的各分类区间进行计算,将9个环境因子的各分类区间按频率比值高低进行重分类,将重分类后的栅格数据进行叠加分析。结合地质灾害易发性指数分布规律,将李家巷镇划分为5个易发性等级区间:极高[0.9,1)、高[0.7,0.9)、中等[0.3,0.7)、低[0.1,0.3)和极低[0,0.1),5个易发区由高至低分别占总面积的2.36%、15.85%、40.41%、41.21%、0.16%,FR模型计算得到的李家巷地质灾害易发性结果如图6所示。由表3可知,极高和高易发区约占地质灾害总面积的93.34%,而极低易发区约占地质灾害总面积的0%,在研究区的中部地区地形平坦灾害发生概率几乎很小,但在该模型分析结果中,有大量的中易发区在中部地区,可见FR模型预测出的易发性结果具有偏差。

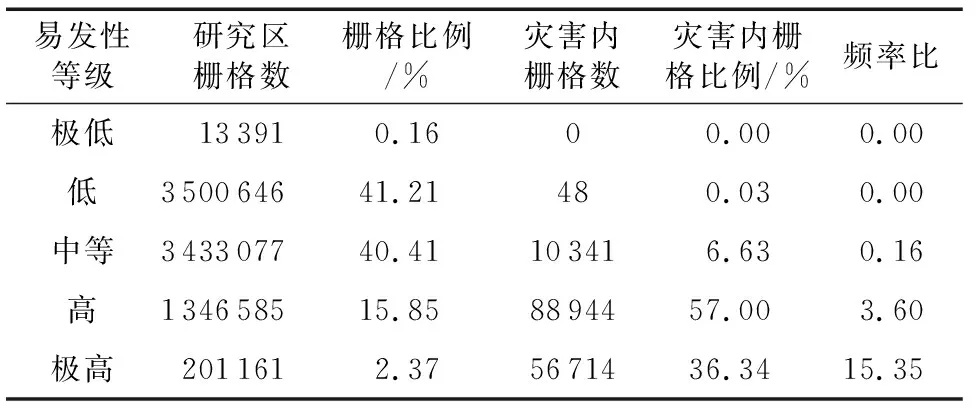
表3 基于频率比模型地质灾害易发性等级的频率比Table 3 Frequency ratio of geological hazard susceptibility grades based on frequency ratio model

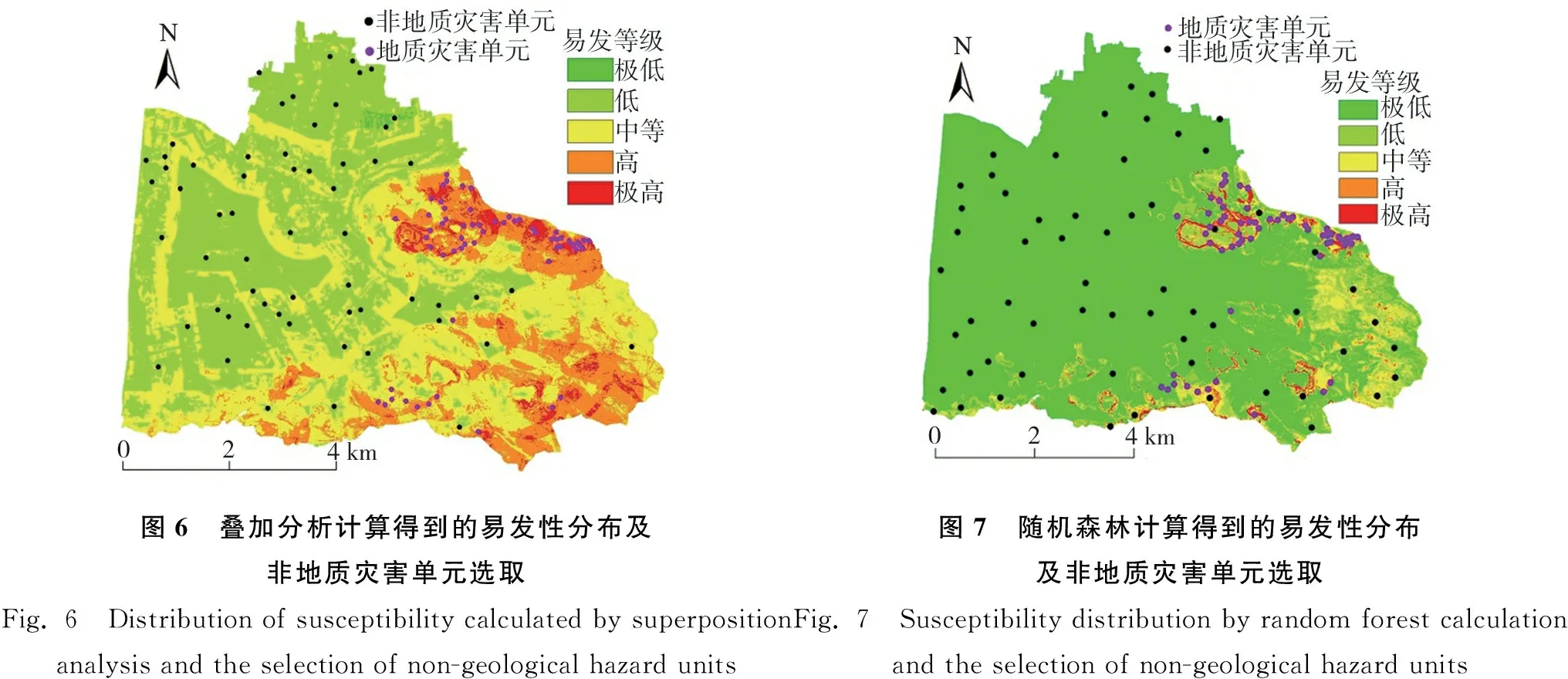
图6 叠加分析计算得到的易发性分布及非地质灾害单元选取Fig. 6 Distribution of susceptibility calculated by superposition analysis and the selection of non-geological hazard units图7 随机森林计算得到的易发性分布及非地质灾害单元选取Fig. 7 Susceptibility distribution by random forest calculation and the selection of non-geological hazard units

由于地质灾害往往发生于暂未发生地质灾害的区域,为避免随机选取的非地质灾害单元落到潜在地质灾害上,在FR模型结果中的低和极低易发区随机选取与已知地质灾害单元样本量匹配的非地质灾害单元,非地质灾害单元的选取结果如图6所示。随机选取的非地质灾害单元主要分布在平原区,部分点分布在坡度较缓的山区,表明经频率比模型筛选非地质灾害单元的空间分布合理。

4.2 随机森林模型

在研究区随机选取与地质灾害单元样本量匹配的非地质灾害单元如图7所示,并将地质灾害单元和非地质灾害单元的集合分为两部分:70%用于模型训练,30%用于模型测试。将地质灾害单元设为1,非地质灾害单元设为0。并将所有环境因子都进行特征标准化处理作为模型的输入变量。采用网格搜索算法和交叉验证对RF模型进行参数优化和检验。计算的易发性结果采用同样的等级分区,5个易发区由高至低分别占总面积的1.53%、1.99%、8.37%、10.66%、77.44%,RF模型计算得到的李家巷地质灾害易发性如图7所示。由表4可知,极高和高易发区约占地质灾害总面积的55.92%,而极低易发区约占地质灾害总面积的7.68%,可见RF模型预测的地质灾害易发性结果也存在一定的偏差。

表4 基于随机森林模型地质灾害易发性等级的频率比Table 4 Frequency ratio of geological hazard susceptibility grades based on random forest model

4.3 频率比-随机森林模型

利用4.1节中选取的非地质灾害单元,并结合地质灾害单元作为RF模型的输入变量,采用网格搜索算法和交叉验证对RF模型进行参数优化和检验。为确保不同模型的易发性评价结果具有可对比性,FR-RF模型的易发性结果同样将研究区划分为5个等级,5个易发区由高至低分别占总面积的9.43%、4.40%、9.60%、4.03%、72.53%。FR-RF模型计算得到的李家巷地质灾害易发性如图8所示。由表5中可知,极高和高易发区约占地质灾害总面积的81.90%,而极低易发区约占地质灾害总面积的0%,可见FR-RF模型具有较高的准确度。

图8 频率比-随机森林计算得到的易发性分布Fig. 8 Susceptibility distribution by frequency radio-random forest calculation图9 评价指标因子的贡献程度雷达图Fig. 9 Contribution degree radar diagram of evaluation index factors

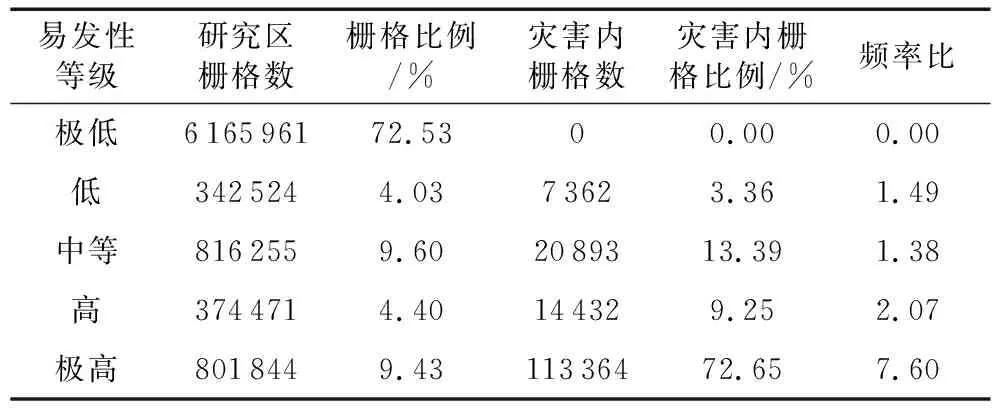
表5 基于频率比-随机森林模型地质灾害易发性等级的频率比Table 5 Frequency ratio of geological hazard susceptibility grade based on frequency ratio-random forest model

RF模型和FR-RF模型两者分析结果都表明了在研究区的东北部和东南部地区是地质灾害的主要发生地区,中部、北部以及南部地区几乎没有地质灾害发生。FR-RF模型在极高和高易发区所占地质灾害总面积数比RF模型高25.98%,在极低和低易发区所占地质灾害总面积数比RF模型低16.7%。由图8可知,FR-RF模型的极高易发区在东北部以及南部边界地带以及中部偏东地区明显高于RF模型,且根据实际调查结果,表明FR-RF模型与实际灾害分布更为吻合,划分效果更好。利用FR-RF模型,得到研究区地质灾害易发性评价因子的贡献程度雷达图如图9所示,结果表明,坡度和工程岩组是该研究区地质灾害的主控因素,相对重要性占比分别为37.7%和28.0%。

5 模型的校验与对比

本文通过接受者操作特性曲线(receiver operating characteristic curve, ROC)下面积(area under curve,AUC)、准确率(Accuracy)、特异性(Specificity)和敏感性(Recall)对模型性能进行评估,其中AUC通常大于0.5小于1,AUC值越大,模型性能越好,采用测试样本绘制ROC曲线,如图10所示。Accuracy是正确预测地质灾害单元和非地质灾害单元的样本占所有样本比例,值介于0和1之间;Recall为能正确预测地质灾害单元的能力;Specificity能正确预测非地质灾害单元的能力。RF和FR-RF模型在测试集上的评估结果如表6所示,FR-RF模型具有较高的AUC、Accuracy、Specificity和Recall,FR-RF模型比RF模型的AUC、Accuracy、Specificity和Recall分别高出6%、11.66%、9.51%和13.71%。FR-RF模型的Recall和Specificity分别为98.33%和93.33%,这表明FR-RF模型对地质灾害单元和非地质灾害单元的预测都具有较好的性能。由此可见,FR-RF具有比随机选取灾害单元的RF模型更高的预测率,能更加有效地反映李家巷地质灾害的分布特征。

图10 模型计算的灾害易发性预测率曲线Fig. 10 Disaster susceptibility prediction rate curves calculated by the model表6 随机森林和频率比-随机森林模型性能对比Table 6 Performance comparison of random forest and frequency ratio-random forest models %评估指标RFFR-RFAUC90.0096.00Accuracy84.1795.83Specificity83.8293.33Recall84.6298.33

6 结论

本文以浙江省长兴县李家巷镇作为研究区,分别采取FR模型、RF模型及FR-RF模型,对研究区进行地质灾害易发性评价,得出如下结论:

1) 本文采用高程、坡度、岩组、剖面曲率、坡向、归一化植被指数、土地利用、距水系距离和距断层距离9个评价因子进行地质灾害易发性评价,经模型重要性分析表明,坡度、工程岩组是该研究区地质灾害的主控因素,相对重要性占比分别为37.7%和28.0%。

2) 根据浙江省长兴县李家巷镇地质灾害发育与分布特征,本文利用FR与RF耦合的方法,确定的非地质灾害单元的选取,建立了FR-RF模型,并对研究区进行了地质灾害易发性评价。FR-RF模型比单一的RF模型AUC、Accuracy、Specificity和Recall分别高出6%、11.66%、9.51%和13.71%。表明FR-RF模型不仅能够有效选取非地质灾害单元,而且对地质灾害单元和非地质灾害单元预测都具有较好的性能,并且在地质灾害易发性预测方面具有较高的精度。

3) 基于FR-RF模型对研究区进行地质灾害易发性评价结果与实际地质灾害分布相对应,极高易发区和高易发区主要分布于存在碎屑岩和坡度较大的区域。随着易发性级别的增大,各等级内地质灾害栅格数量随之增大,说明采用FR-RF模型确定的易发性分区与实际地质灾害发生情况相吻合。