航空永磁电驱动系统比例谐振型自抗扰速度控制器设计

陈哲，陈沛阳，滕国飞，李金程，骆光照

1.西北工业大学，陕西 西安 710072

2.航空工业西安航空计算技术研究所，陕西 西安 710065

随着全电/多电飞机的快速发展，高功率密度机电作动器（EMA）在飞机飞行控制系统中得到了极大的推广，其大多采用具有高功率密度和高效率的永磁同步电机（PMSM）[1-3]。在飞机高升系统的襟缝翼EMA中，需要加、减速度快和速度控制精度高[4]。襟缝翼翼面在飞行中的气弹性载荷表现为周期性扭矩载荷[5]，对PMSM驱动器的速度控制精度产生很大影响。根据文献[6]、文献[7]中的分析，气动载荷或颤振的频率范围为25～250rad/s，并高度依赖其翼型的几何设计和材料特性。因此，设计出一种抗干扰能力强的速度控制器对提升航空EMA性能具有重要意义。

现有的比例积分微分（PID）速度控制器在周期性负载扰动存在时控制性能受限。为了设计一种更具抗周期干扰能力的速度控制器，许多学者尝试采用基于模型的控制策略，如模型预测控制[8]和内部模式控制[9]，以及无模型速度控制策略，如重复控制（RC）[10]和迭代学习控制（ILC）[11]。在过去的10年中，自抗扰控制器（ADRC）在EMA领域中也得到了广泛关注，其中线性型 ADRC（LADRC）的数学描述直观，并且方便采用传递函数进行分析[12]。本文采用LADRC 作为速度控制器。为了抑制速度环的周期性负载干扰，在ADRC 中加入比例谐振控制作为扩张状态观测器的一部分。本文提出的速度控制器保持了传统LADRC的优势，并对特定次周期性干扰有较强的抑制能力，可以实现襟缝翼机电作动器高精度的速度控制，为飞机平稳起降提供技术支撑。

1 机电作动器速度控制

1.1 系统结构

图1所示为机电作动系统的示意图，其主要包括飞控计算机、作动器控制单元、供电电源、PMSM、减速器和丝杠等组成部分。首先由飞控计算机下达位置或者速度指令，作动器控制单元采集永磁同步电机的位置信息和线性可变差动变压器（LVDT）的直线位移信息，最终完成高动态的位置或者速度闭环控制，使舵面偏转到指定的角度。

图1 机电作动系统示意图Fig.1 Diagram of flight EMA system

永磁同步电机控制系统如图2所示，主要包括位置环、速度环、电流环三个控制回路。

1.2 速度环扰动分析

永磁同步电机驱动器中速度环扰动包括非周期性扰动和周期性扰动。非周期性扰动主要由阶跃等非周期性负载转矩引起。另外，电机参数的变化、电流回路跟踪误差，摩擦力矩、未模型化的电机转子及减速器和丝杠的动力学特性等也会产生周期性扰动。周期性扰动通常由诸如齿槽转矩、磁通谐波等齿槽效应和涡流效应引起。本文着重考虑气动周期性负载扰动。

2 比例谐振型ADRC速度控制器

2.1 速度环解耦型ADRC控制器设计

永磁同步电机机械方程为

式中，TL为负载转矩；J为转动惯量；pn为极对数；ωe为电角速度；B为黏性摩擦系数；g(t)为其他扰动，包括非周期性和周期性扰动；Te为电磁转矩，可表示为

2.2 PR-ADRC的设计

为了抑制周期性的负载转矩扰动，本文提出了PR-ADRC的速度环，与传统LADRC相比，有两步改进，如图3所示。

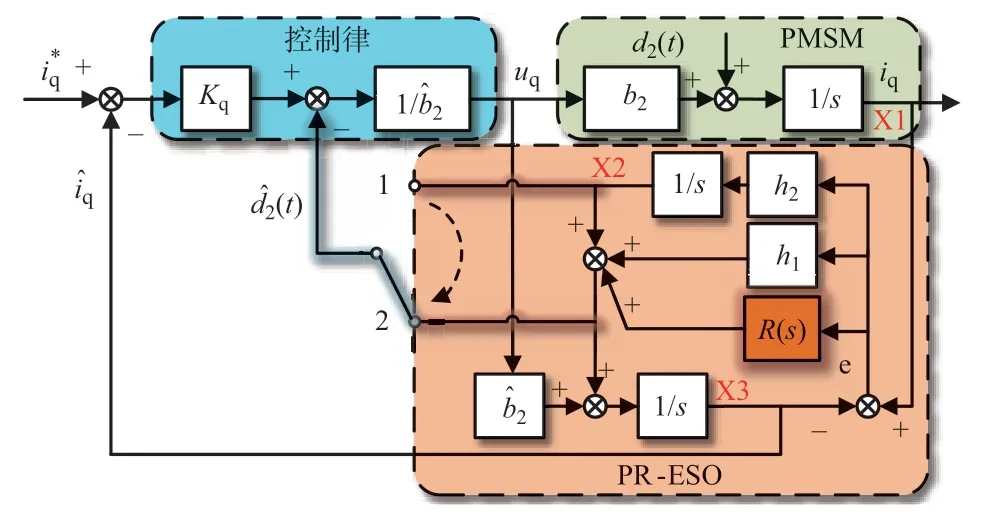
图3 基于LADRC的速度环和提出的PR-ADRC框图Fig.3 Block diagram of speed controller based on LADRC and the proposed PR-ADRC

式中，h1+R(t)组成了ESO中的PR控制器。一旦估计得到了周期性的负载转矩扰动频率ωeso，提出的带PR控制器的ESO可以更有效地估计相应的扰动。

Gf3(s) 仅与隐藏在h1和h2中的ωeso有关。它取决于Kr，ωc和ωload。

图4 展示了相同条件下，ωload设置为100rad/s 时，Gf1(s)、Gf2(s)和Gf3(s)的波特图的对比。显然，在谐振频率，Gf3(s)有更好的抗扰动能力。

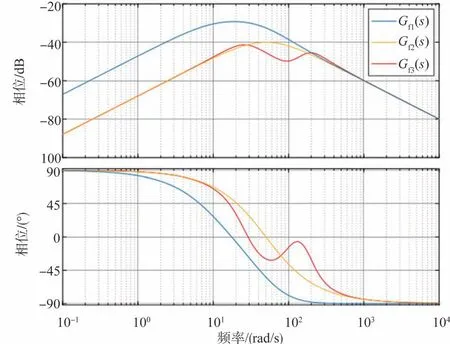
图4 Gf1(s)，Gf2(s)和Gf3(s)的波特图对比Fig.4 Bode diagram comparison between Gf1(s)，Gf2(s)and Gf3(s)

3 试验验证

本文在基于Higale的实时仿真平台上对提出的速度环比例谐振型自抗扰控制算法进行了试验验证。试验电机参数见表1，控制系统参数见表2。为了保证试验验证结果对比的合理性，本文参考文献[13]中的PI 参数计算方法统一设置了电流内环带宽。PI速度环和LADRC速度环带宽设置和PR-ADRC保持一致。

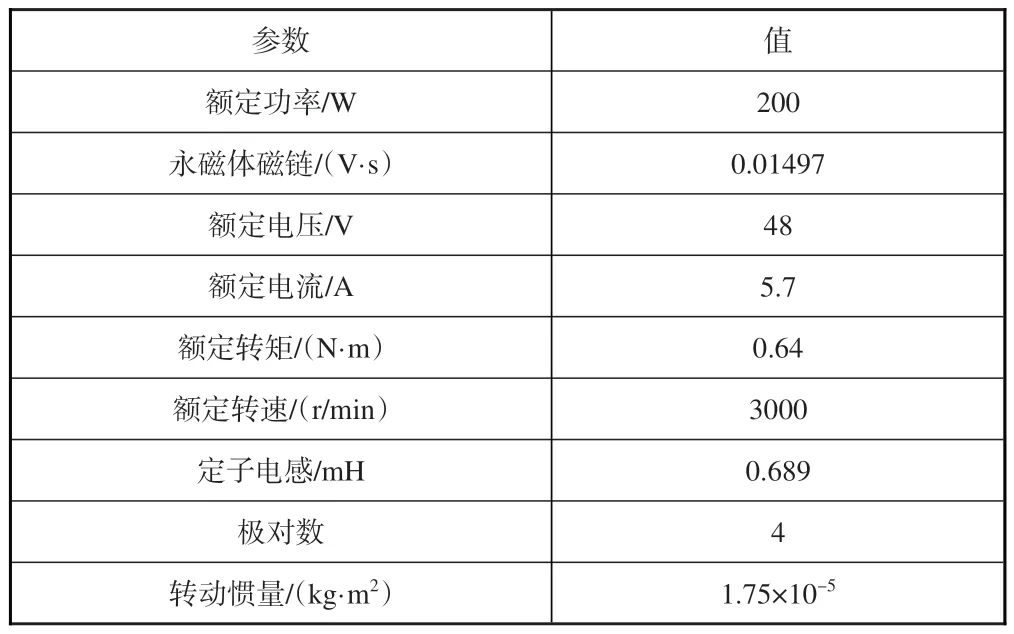
表1 试验永磁同步电机参数Table 1 Parameters of PMSM under test

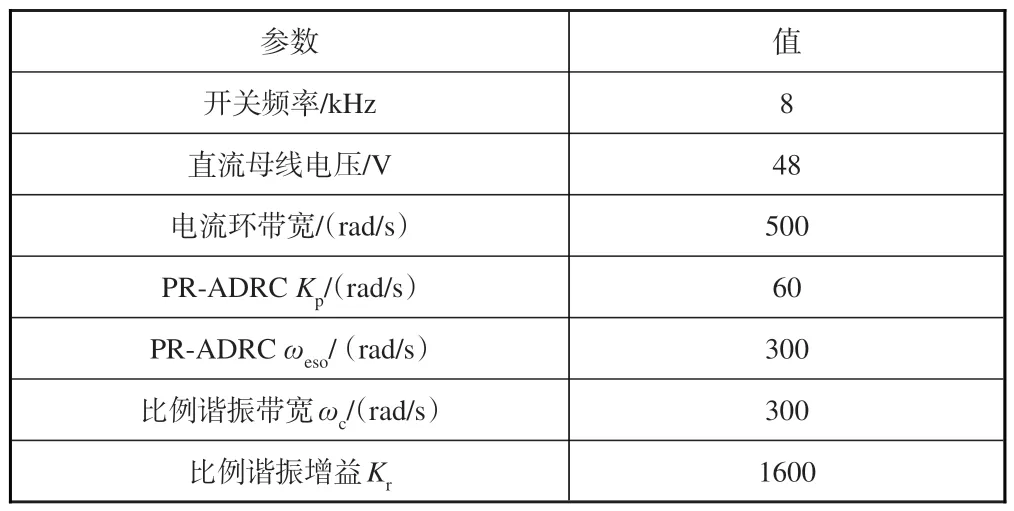
表2 控制系统参数Table 2 Parameters of PMSM controller

3.1 额定转速下周期性扰动试验

在额定转速3000r/min 况下，设置负载转矩由初始的0.1sin(100t)N·m 变为0.1sin(200t)N·m，测试三种不同速度控制方式下转速控制的性能，试验结果如图5 所示，从上至下分别为负载转矩、PI 控制器、LADRC 控制器和提出的PRADRC控制器的转速控制效果。从图5中可以看出，在负载转矩为0.1sin(100t)N·m时，PI控制器、LADRC控制器和PRADRC 控制的转速波动分别为66r/min、59r/min 和21r/min。当周期性负载变为0.1sin(200t)N·m后，这三种速度环控制方法的转速波动最大值分别为76r/min、66r/min和25r/min。可以明显看出，本文所提出的PR-ADRC在变周期性负载扰动下对转速的控制更为平稳。

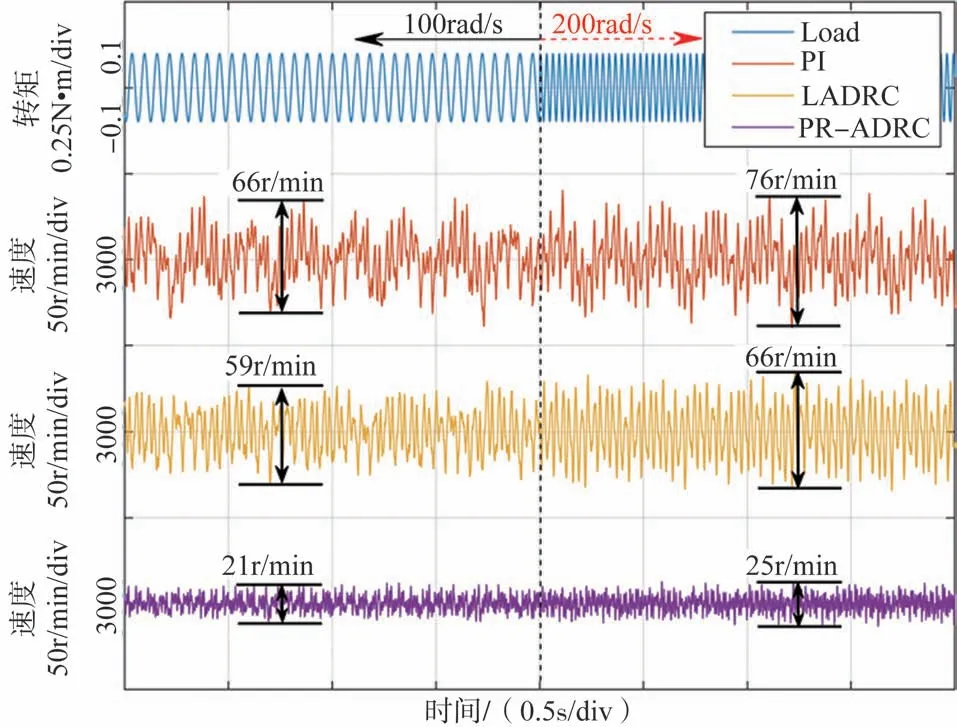
图5 额定转速下周期性负载转矩变化三种控制方法试验结果Fig.5 Experimental results at rated speed with load torque frequency variation for three different control strategies

3.2 周期性负载下负载阶跃试验

在转速为1000r/min 条件下，根据气动载荷或颤振的频率范围[7]选取负载转矩为0.1sin(200t)N•m+0.15N·m，即在固定周期性负载条件下叠加一个阶跃负载，同样对三种速度环控制方法的速度控制性能进行对比验证，试验结果如图6所示，从上至下分别为负载转矩，PI 控制器、LADRC 控制器和提出的PR-ADRC控制器的转速控制效果。从图6中可以看出，在负载转矩为0.1sin(200t)N•m 时，PI 控制器、LADRC 控制器和PR-ADRC控制的转速波动分别为43r/min、47r/min和19r/min。当阶跃负载0.15N·m叠加以后，三种速度环控制方法的转速跌落最大值分别为171r/min、132r/min 和57r/min。待动态调节过程结束，实际转速恢复至设定值1000r/min后，三种速度环控制方法的转速波动分别为62r/min、66r/min 和42r/min。从该试验中也可以明显看出，本文提出的PRADRC速度控制器有着优异的转速控制性能。

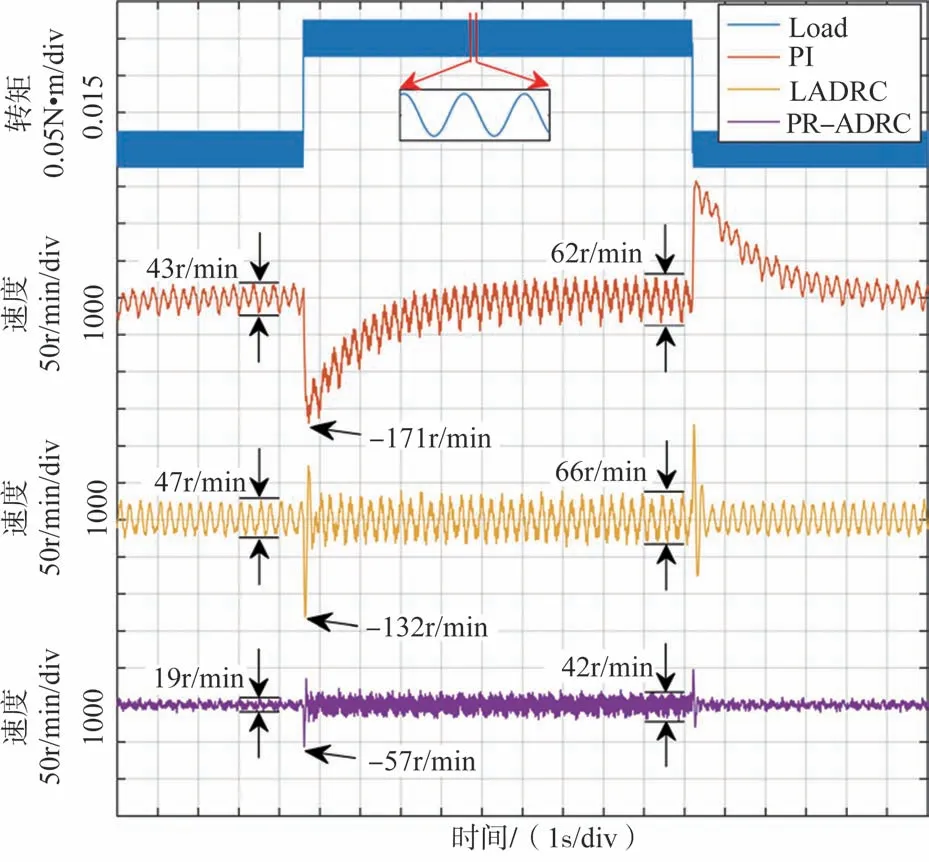
图6 周期性转矩下转矩阶跃试验结果Fig.6 Experimental results under two different load torque disturbance with three different control strategies

4 结论

本文提出了一种PR-ADRC 速度控制器，以抑制周期性负载扰动并提高速度控制精度。为了解决现有PI 和LADRC 速度控制器的缺点，本文所提出的PR-ADRC 速度控制器更改了反馈路径，并在ESO 中添加了谐振控制器。试验结果表明，本文所提出的方法可以显著抑制非周期性干扰和周期性干扰，并且对电机参数变化具有良好的鲁棒性。同时，本文的研究成果还对于永磁同步电机控制系统在速度控制精度高和加、减速度快的场合下的应用实现具有工程意义。