可变形式翼型钝体的风致振压电俘能器

张忠华，李 哲，孟凡许，王淑云，李 赫，阚君武

（浙江师范大学 精密机械与智能结构研究所，浙江 金华 321004）

1 引言

随着微功率便携式电子产品和无线传感器节点的自供电需求越来越高，寻求一种可持续、安全稳定的俘能技术成为了国内外学者讨论的热点话题，为此人们对以电磁、摩擦、压电等原理为基础的俘能器进行了多方面的研究［1-4］。电磁式适用于高速旋转环境、摩擦式适用于微表面接触环境，相较于前两者，压电俘能器的优势在于结构简单，易集成一体化微机电系统、无电磁干扰及对材料的损耗较小等［5-7］。根据应用领域工作环境中存在能量的不同，压电俘能器大致可分为风致振式［8］、旋转式［9］、振动式［10］三类。其中，风致振压电俘能器主要依靠钝体受风力影响产生振动激励压电陶瓷进行发电，其根据激励钝体的结构主要分为三类，分别为单钝体式、多钝体式及复合钝体式，三者各有特色，单钝体式的研究最为普遍，在此基础上的多钝体及复合钝体式振动特性多样，已然成为风致振压电俘能器的研究前沿。

早期，学者们主要研究的是卡门涡街对海洋建筑物的振动损害［11］，但随着研究的深入，利用单钝体在这种振动中的特性进行俘能的方法逐渐成为热点话题。2019 年，Wang 等人［12］通过在风力作用下圆柱壳体所产生的涡振间接激励壳体内的压电悬臂梁振动发电，有效避免了环境对发电单元的影响，且最佳负载下的功率可达0.4 mW。2021 年，Liu 等人［13］提出一种顺流激励式Y 型钝体压电俘能器，试验表明半角为60°的Y 型钝体使俘能器输出电压提升了近十倍。2022 年，侯成伟等人［14］将圆柱钝体涡振式俘能器放在可转动圆盘上，通过圆盘的导向翼自主调节迎风角度，从而大幅提高了其在多风向环境中的适应能力。综上，单钝体式俘能器具有结构简单、理论基础深厚的优势，但由于钝体单一固定，振动特性几乎不可调，无法适应多变的环境从而导致发电效率较低。

为改善单钝体式压电俘能器的振动特性并提高其发电性能，多钝体及复合钝体式应运而生。多钝体式指两个及以上独立存在钝体共同影响俘能器工作，2021 年，Hu 等人［15］提出了一种由方柱钝体和梳状钝体共同作用的压电俘能器，相较于单一方柱钝体，它降低起振风速的同时输出功率提高了约171.2%；2022 年，Liao 等人［16］在圆柱壳体后方安置了一个矩形定钝体来改善原有振动特性，实现了小振幅涡振向大振幅驰振的转变，使其输出功率达到近2.22 mW；2023 年，Kan 等人［17］提出了一种顺流激励式双钝体压电俘能器，通过下游挡板钝体扰动上游圆柱钝体的流场来弥补顺流激励振幅小的缺陷，提升高风速下俘能器的结构可靠性及发电能力。复合钝体式指在单一钝体上耦合一种及以上部件来改变俘能器原有的振动特性，2020 年，Wang 等人［18］提出一种不同横截面的混合钝体式风致振压电俘能器，通过调节钝体中圆柱与方柱的占比以及迎风面形状改善流固耦合特性，使其最大输出电压提高71%；2021 年，该团队又设计了一种非光滑圆柱钝体来改变涡振特性［19］，研究表明，不同表面的圆柱钝体可以增强或抑制系统的振动，以期适用于不同的工作环境。综上，多钝体结构或复合钝体结构能有效改善俘能器的振动特性，降低其起振风速、扩宽工作风速范围，但这两类俘能器多数以驰振形式工作，容易造成发电单元的损坏，故其高风速环境下的适应能力还存在提升空间。

除此之外，近几年还出现了一种可变钝体式的风致振压电俘能器，2018 年，Zhou 等人［20］提出利用弯曲机翼的Y 形钝体所产生的相干共振来提高低速气流的俘能效率；2020 年，Sun 等人［21］提出一种滑动式圆柱钝体的风致振压电俘能器，实现拓宽锁频范围、提高平均功率的目的。综上，该类俘能器为风能的采集开辟了新方向。

针对上述各类问题并结合现有研究，本文提出一种可变形式翼型钝体的风致振压电俘能器，它主要由可变式翼型钝体（弹性翼+刚性翼）、悬臂梁及压电组合梁构成，钝体的弹性翼受风力影响产生形变，从而实现系统振动特性的自我调节，以期达到降低起振风速、拓宽工作风速范围及限制高风速系统振幅的目的。通过建模仿真和试验两种方法研究结构参数（钝体迎风角和弹性翼刚度）、风速及负载电阻对俘能器输出特性的影响规律，证明该结构原理能够提高其环境适应性，为构造满足自供电需求的俘能器后续研究提供了新思路。

2 俘能器的结构与工作原理

可变形式翼型钝体风致振压电俘能器的结构原理如图1 所示，主要由基座、悬臂梁、垫块、铜基板、压电陶瓷、刚性翼及弹性翼组成。其中，垫块、铜基板和压电陶瓷三者构成压电组合梁，并安装在悬臂梁的两侧，呈对称分布；刚性翼和弹性翼构成可形变式翼型钝体，并安装在悬臂梁的自由端。钝体的迎风角由两片刚性翼组成的角度决定，钝体的形状则通过弹性翼在风力作用下产生的变形量决定；压电组合梁自由端的垫块可实现振动能力的间接传递，避免压电陶瓷因承受超过许用应力的拉应力而损毁［22］。

图1 俘能器的结构示意图Fig.1 Structure diagram of energy harvester

风致振压电俘能器主要通过风经过钝体后在其两侧表面产生的交替漩涡促使钝体连带着悬臂梁进行往复摆动，从而间接激励压电组合梁变形发电，同时钝体形状主要由弹性翼变形量决定，因此可以通过弹性翼受风速影响的大小来改变俘能器的流固耦合及振动特性。为直观体现出风速对俘能器工作过程及钝体形状的影响，采用COMSOL 仿真对其进行了模拟试验，获得了俘能器的输出电压波形及工作过程，分别如图2和图3 所示，其中图3 是分别在不同风速下提取一个振动周期T内的波峰（0.25T）、平衡位置（0.5T）及波谷（0.75T）的振动形态组成的。根据图中俘能器钝体形状和输出电压大小的变化，将工作过程分为两个阶段：

图2 输出电压的波形图Fig.2 Output voltage waveform

图3 风速v 不同时俘能器的工作过程Fig.3 Working process of the energy harvester wIth different wind speeds

（1）发散性振动阶段：当风速在0～10 m/s 之间时，弹性翼变形较小，钝体迎风面呈V 字形，其振幅及输出电压均随着风速的增加而增大，结合流体力学理论和现有关于V 型钝体的研究［13，23］，此时俘能器主要以驰振的方式工作，其中风速v=5 m/s 和v=10 m/s 时的俘能器工作过程分别如图2（a）和图2（b）所示；

（2）收敛性振动阶段：当风速在10～15 m/s之间时，弹性翼变形较大，钝体迎风面呈弯弧状，其振幅及输出电压均随风速的增大而出现减小趋势，而这种迎风面类似于圆柱钝体表面的形状，根据流力力学理论和现有关于圆柱钝体的研究［24］可知，在这一风速范围内，俘能器是以类似涡振的方式进行工作，基本实现通过钝体形状随风速变化而变化的特性来防止系统振幅无限制增大的目的，其中风速v=15 m/s 时的俘能器工作过程如图2（c）所示。

3 有限元建模与仿真

为研究可变形式翼型钝体迎风角和弹性翼刚度对俘能器的流固耦合特性及输出性能的影响规律，利用COMSOL 对不同参数下的俘能器进行了模拟仿真，其中由于本文研究重点在于钝体及其形变状态，故将压电组合梁简化成单层的压电陶瓷，几何模型的基本结构参数及材料如表1 所示。

表1 俘能器的基本结构参数及材料表Tab.1 Basic structure parameters and materials of the energy harvester

图4 为俘能器的几何模型及流场设置，其中作为变 量的迎风角θ分别为0°，40°，80°，120°，160°及180°；弹性翼刚度因测量不便，将其厚度e作为刚 度变量，其分别 为0.15 mm，0.3 mm，0.45 mm，0.6 mm 及0.75 mm。此外，仿真时采用的测试风速为10 m/s，出口压力为0 Pa；本文采用宽为钝体总翼长10 倍（400 mm）、长为其20倍（800 mm）的流场进行测试［25］。

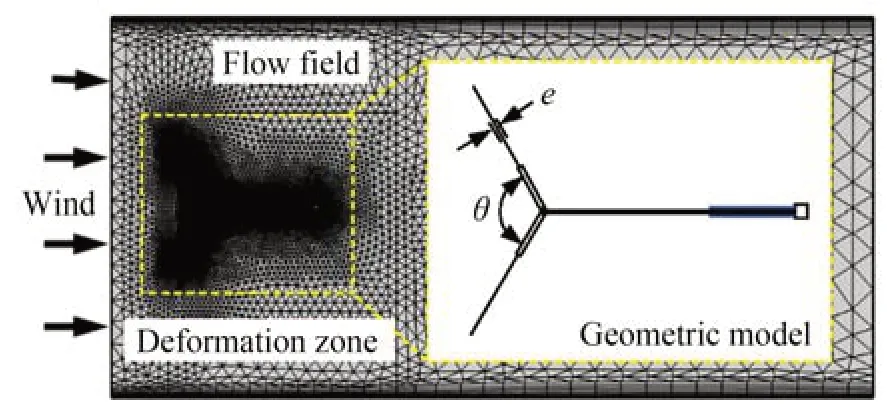
图4 俘能器的几何模型及流场设置Fig.4 Geometric model and flow field setting of energy harvester

图5 为迎风角和弹性翼厚分别作为变量时的风场流速分布及压力等值线云图。由图可知，当θ=0°，e=0.15 mm 时，压力等值线分布均匀，且钝体两侧流速基本一致，俘能器无法起振，但随着θ的增加，俘能器周边的涡流分布密度和最大压力差均呈先增大后减小趋势；当θ=120°、e作为变量时，弹性翼形变量、涡流数量及最大压力差均随着e的增大而逐渐增大。

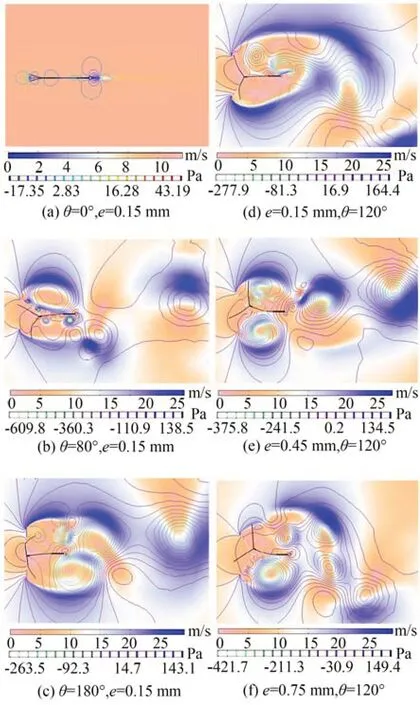
图5 不同变量下的风场流速分布及压力等值线云图Fig.5 Velocity distribution and pressure contour cloud map of wind field under different variables

图6 为迎风角θ、弹性翼厚e分别作为变量时的输出电压波形图。由图6（a）可知，当迎风角θ=0°时，由于钝体迎风面积较小，无法产生交替脱落的涡流促使其起振，但当0°＜θ≤80°时，涡流所提供的压力差随迎风角θ增加而增大，故俘能器输出电压呈增大趋势；当80°＜θ≤180°时，由于涡流压力差及分布密度的减小，俘能器输出电压呈小幅下降趋势。由图6（b）可知，随着弹性翼厚e的增加，俘能器输出电压会出现小幅上涨，由此表明，降幅的效果随着弹性翼刚度的增大而减小。综上，选择合适迎风角θ和弹性翼厚e能够实现控制钝体振幅、有效降低俘能器起振风速及提高发电能力的目的，为后续俘能器的设计、制作和试验测试提供了理论依据。

图6 迎风角θ、弹性翼厚e 分别作为变量时的输出电压波形图Fig.6 Output voltage waveform diagram with windward angle θ and elastic wing thickness e as variables respectively

4 试验测试与分析

为验证该俘能器结构的可行性及仿真结果的正确性，制作并搭建了如图7 所示的试验样机及测试系统，其结构尺寸和所用材料与仿真基本相同（详见表1），不同之处在于试验样机采用三维结构，其钝体高度为50 mm，悬臂梁宽度为20 mm，压电陶瓷的直径和厚度分别为18 mm 和0.2 mm，铜基板直径和厚度分别为26 mm 和0.3 mm。试验所用仪器包括：DS5042M 型数字存储示波器、测试风机、变频器、风速仪、电阻箱等。试验中调节变频器频率来间接改变风机的风速，经风速仪测量二者近似呈线性关系（v=0.75f），变频器步长1 Hz，测试风速范围为0～25 m/s。试验中所提到的输出电压U均为单片压电陶瓷的开路峰峰值电压，输出功率P为单片压电陶瓷的峰峰值功率，且主要研究的变量为迎风角θ（0°/40°/80°/120°/160°/180°）和弹性翼厚e（0.15 mm/0.3 mm/0.45 mm/0.6 mm/0.75 mm）。

图7 试验样机及测试系统Fig.7 Test prototype and test system

为验证不同风速区域内俘能器拥有不同的振动特 性，选取迎风角θ为120°、弹性翼 厚e为0.15 mm 的俘能器进行试验，获得了不同振动状态时的电压波形及输出电压与输入风速的关系曲线，分别如图8（a）和图8（b）所示。由图可知，俘能器大致有四种振动状态：

（1）无振区：当风速v在0～3.24 m/s 之间时，输出电压微弱，俘能器处于静止状态还未起振，产生波形的主要原因为试验台的微振动以及示波器内置电压的干扰；

（2）增幅区：当风速v在3.24～8 m/s 之间时，由于压电组合梁主要受单向力作用，电压波形呈周期性非对称曲线，此时钝体因风速较小未发生过大变形，整体呈V 型，而根据流体力学理论及现有关于V 型钝体的风致振压电俘能器的研究可知，俘能器输出电压会随着风速的增加而快速增大的工作方式，属于驰振；

（3）等幅区：当风速v在8～17 m/s 之间时，电压波形与增幅区波形除了幅值外基本一致，俘能器逐渐由驰振转为涡振，输出电压不再随风速的增加而增大，而是达到最大值后维持在一个小范围内上下波动，出现近似“锁频”的状态；

（4）降幅区：当风速v在17～25 m/s 之间时，电压波形的频率较高但电压值有所减小，此时钝体迎风面受强风影响变为弯弧状，而这种类似于圆柱钝体表面形状的钝体，根据流体力学理论和现有关于圆柱钝体的风致振压电俘能器的研究可知，俘能器输出电压在某一风速带内较大，此后会随风速增大而减小的工作方式，属于涡振。

图9 为弹性翼厚e=0.15 mm、迎风角θ不同时输出电压U与输入风速v的关系曲线，图10 为提取不同迎风角θ下的起振风速v0、锁频风速vf（俘能器完全起振并刚进入等幅振动时的风速）、降幅风速vd及等幅电压Uc构成的规律曲线。由图9 可知，在试验风速范围内，随着风速v的增加，迎风角θ在0°～80°范围内的俘能器会出现失稳现象（如图中A，B，C点所示），即悬臂梁产生过大变形以致偏转到一边无法回到平衡位置，而迎风角θ在80°～180°范围内的俘能器随风速增大基本会出现无振、增幅、等幅及降幅四种振动状态，且随着迎风角θ的增加，等幅振动的风速范围出现减小趋势，同时降幅区输出电压下降的速率逐渐增大，系统涡振特性愈发明显。由图10 可知，在试验迎风角范围内，俘能器的起振风速v0随迎风角θ的增加呈先减小后增大的趋势；当迎风角θ＜40°时俘能器在起振过程中出现失稳现象，当迎风角θ≥40°时俘能器出现等幅电压Uc，且其值随迎风角θ的增加呈波动式下降趋势，但锁频风速vf随迎风角θ增大呈先减小后增大的趋势；当迎风角θ＜120°时俘能器基本不会出现降幅现象，而当迎风角θ在120°～180°之间时，俘能器出现涡振特性，且降幅风速vd随迎风角θ的增加而减小。

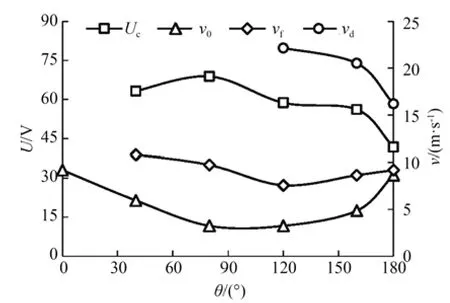
图10 迎风角θ 对起振风速v0、锁频风速vf、降幅风速vd及等幅电压Uc的影响规律曲线Fig.10 Influence of windward angle θ on vibration velocity，frequency locking velocity，drop velocity and constant amplitude voltage

图11 为迎风角θ=120°、弹性翼厚e不同时输出电压U与输入风速v的关系曲线，图12 为提取不同弹性翼厚e下的起振风速v0、锁频风速vf、降幅风速vd及等幅电压Uc构成的规律曲线。由图11 可知，在试验风速范围内，当弹性翼厚e＞0.3 mm 时，俘能器在较高风速下会出现失稳现象（如图中D，E，F点所示）；当弹性翼厚e≤0.3 mm 时，随风速增大俘能器均会出现等幅、降幅现象，确保了其结构的安全可靠。由图12 可知，俘能器的起振风速v0受弹性翼厚e影响较小，但锁频风速vf和等幅电压Uc均会随着弹性翼厚e的增加而小幅增大，且当弹性翼厚e≤0.3 mm 时，俘能器的降幅风速vd也随着弹性翼厚e的增加而增大，有效拓宽了其稳定工作的风速范围。

图11 弹性翼厚e不同时输出电压与输入风速的关系曲线Fig.11 Relation curve between output voltage and input wind speed when elastic wing thickness e is different

图12 弹性翼厚e 对起振风速v0、锁频风速vf、降幅风速vd及等幅电压Uc的影响规律曲线Fig.12 Influence of elastic wing thickness e on vibration velocity，frequency locking velocity，reduction velocity and constant amplitude voltage

综上，存在迎风角θ为120°～160°、弹性翼厚e为0.15～0.3 mm 时，俘能器的起振风速较低、工作风速范围较宽，同时其振幅不会因风速的增加而无限制增大，提高了俘能器的环境适应性，且试验所获得的规律与仿真分析结果基本保持一致，证实了仿真模型的正确性。

图13 为 弹性翼厚e=0.15 mm、迎风角θ不同时输出功率P与负载电阻R的关系曲线，分别选取三个较为合适的迎风角θ（80°，120°及180°），然后在15 m/s 的风速激励下通过调整负载电阻找到该俘能器的匹配阻抗，以此获得它们的最大输出功率。由图中可知：存在最佳的负载电阻（250 kΩ）使该俘能器的输出功率达到最大，当迎风角θ为80°，120°及160°时，俘能器最大输出功率分别为3.78 mW，2.65 mW 及2.52 mW。

图13 迎风角θ 不同时输出功率与负载电阻的关系曲线Fig.13 Relation curve between output power and load resistance when windward angle θ is different

5 结论

为降低起振风速、拓宽工作风速范围及限制高风速下的系统振幅，本文提出一种可变形式翼型钝体的风致振压电俘能器，并通过仿真与试验研究了不同风速下弹性翼厚和迎风角对俘能器输出性能的影响规律，获得如下结论：

（1）俘能器的钝体由于存在可变形的弹性翼，钝体的形状会随着风速变化而改变，从而使俘能器达到自适应风速调节自身振动特性的目的。当风速较低时，弹性翼形变较小，钝体呈V字形，其振幅随风速增大而增大，此时系统以驰振为主；当风速较高但还未超过阈值时，弹性翼形变增大，钝体呈曲面翼型，其振幅不再随风速增加而大幅变化，此时系统进入“锁频”状态；当风速超过阈值时，弹性翼变形较大，钝体呈弯弧状，其振幅随风速增加而逐渐减小，此时系统以涡振为主。因此，俘能器钝体形状适应风速而变化的特性能够使得输出电压随风速增大呈先增大后平缓再减小的趋势；

（2）迎风角和弹性翼厚对钝体形状变化及其振动特性的影响较大。在试验范围内，当迎风角小于120°时，俘能器在较高风速下会出现失稳现象，从而导致其结构易发生损坏；而当迎风角在120°～180°之间时，俘能器能够在较高风速下稳定发电，且随着迎风角的增大，起振风速呈增大趋势，锁频风速呈先减小后增大趋势，降幅风速和等幅电压则基本呈减小趋势。当弹性翼厚大于0.3 mm 时，俘能器由于弹性翼刚度过大产生变形较小，无法改变发散性振动特性而出现失稳现象；但当弹性翼厚不大于0.3 mm 时，俘能器的振动特性会适应风速的变化，且锁频风速、等幅电压及降幅风速均随弹性翼厚增加而增大；

（3）当选择较佳的迎风角（120°～160°）、弹性翼厚（0.15～0.3 mm）时，俘能器的起振风速可降至3.24 m/s，稳定工作风速至少可达25 m/s，且存在最佳负载为250 kΩ 时俘能器的最大输出功率为3.78 mW。