基于模糊免疫自适应PID的风力发电机励磁控制方法
2024-01-04李世明林玥廷曾凯文龙建平
戴 月,李世明,林玥廷,曾凯文,龙建平
(1.广东电网电力调度控制中心,广东 广州 510600;2.湖南大唐先一科技有限公司,湖南 长沙 410007)
0 引言
目前,保证电网的供电质量变得越来越重要,同步发电机励磁控制是电网中的一个关键环节,其运行的好坏将直接关系到电网电压波动、无功功率分布和抗干扰性等。另外,它还可以对励磁控制系统进行额外的控制,以有效地抑制磁同步振荡,从而保证电网的稳定运行。但在实际操作中,需要保证发电机的励磁性能,为此,较多学者对风力发电机励磁控制方法展开了研究。其中,杨琦等[1]研究了基于模糊控制虚拟电阻的双馈风力发电机低电压穿越励磁控制方法,通过将模糊控制技术引入到常规的虚拟电阻中,实现了在失效过程中跟踪系统动态变化的模糊控制,并在不超过容许范围的情况下,实现控制;苏显贺[2]研究了新型直驱交流励磁风力发电系统控制策略,该策略重点对电网电压定向矢量控制,调节直流母线的电压以及功率因数,并对磁链方向进行了控制,实现励磁电流的控制。
上述方法虽然能够实现发电机励磁控制,但是由于进行风力发电机励磁控制的过程中没有考虑发电机内部状态变化以及非主要电路的控制作用,导致控制后的电压、电流和输出功率均不稳定。而模糊免疫 PID基本思想是:通过量化因子将控制器输入的输入量投影到 Fuzzy论域中,获得模糊量,然后根据所设置的模糊规则进行模糊操作,最终通过比例因子解模糊,从而获得更好的控制效果。为此,本文提出基于模糊免疫自适应PID的风力发电机励磁控制方法,解决当前存在的问题。
1 励磁系统建模
风力发电机励磁控制对于电力系统稳定性起着非常重要的作用,为有效控制,建立基于励磁控制系统中各项参数的模型[3]。为了简化计算,对实际的风力发电机作必要的假定:
a.忽略磁饱和因素和涡流引起的损失,把电动机磁体的磁导系数记为1个常量。
b.假定发电机的结构在空间上是完全对称的。
c.在发动机内部,空气间隙的磁场是均匀[4]的。
d.忽略交流励磁系统的减振性能。
e.考虑非可控整流器的换相过程。
f.交流励磁电机的转速是恒定的。
g.考虑励磁系统的饱和作用。
h.交流励磁电机的定子压降未被计算在内。
i.不考虑由整流器本身引起的压力损失。
基于以上假设,建立无刷励磁系统数学模型,主要内容如下:
a.风力发电机数学模型,在电力系统机构中,风力发电机数学模型结构较为复杂,并且内部有机械运动部件,所以其传递函数较为复杂[5]。为简便分析,需要对其简化,简化后的传递公式为
(1)
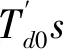
b.电压测量与比较单元的数学模型[6],电压测量单元能够将发电机的输出电压变为正比的直流电压,将一阶滞后环节表示为
(2)
UG为风力发电机的输出端电压值;Udc为比较单元输出的参数向量;KR为电压的增益值;TR为测量电路的时间常数;s为输入量。
c.移动触发与功率单元的数学模型,移动触发单元由触发器、放大电路等组成[7],同时整流电路供电的交流电之间存在一定延迟,将延迟的公式表示为
(3)
f为交流电源频率;m为电路相数。
将输电线路总的传递函数[8]表示为
(4)
KZ为第Z个指标的放大增益量;TZ为第Z个功率模块的输出参数。
上述计算没有考虑发电机内部状态变化以及非主要电路的控制作用,因此,将风力发电机励磁系统转换为单输入与单输出的系统,并得到传递函数,方便后续的风力发电机励磁控制。
2 模糊免疫 PID 励磁控制器设计
模糊免疫自适应PID的原理是:人体免疫系统在遇到外来入侵的时候,会生成对抗机制,即抗体,在对抗后会与抗原结合,从而发生一系列的反应,破坏抗原[9]。因此,本文采用免疫PID算法对风力发电机励磁控制。首先,根据免疫反馈理论设计了PID控制器,该控制器的结构如图1所示。
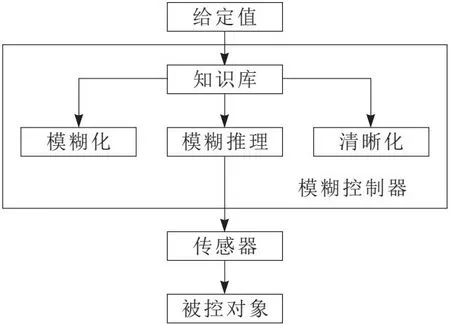
图1 模糊免疫自适应PID控制器结构
将免疫反馈控制[10]公式表示为
s(k)=(k1-k2f(Δs(k)))ε(k)
(5)
k、k1、k2分别为控制结构中的非线性函数、激励函数以及抑制函数;f为抑制参数;Δs为抗原数量;ε为刺激后输出的细胞参数。
免疫的作用就是在保持免疫系统稳定性的同时,对外来的抗原作出反应,这是因为抗原会对机体造成伤害,也有可能是因为抗体浓度太高,会对机体造成伤害,所以必须要控制住[11]。而免疫系统的总体目标是尽可能地减少机体所遭受的整体损伤,以确保在动态调整过程中能迅速地消除这些误差[12]。基于上述分析,将公式表示为
u(k)=K(1-ηf(u(k),Δu(k)))e(k)
(6)
η为超调量;u(k)、e(k)分别为抑制细胞的抑制量。
从以上程序可以看到,模糊免疫系统是一种非线性控制器,其中涉及的比例系数会随着控制器的输出而发生变化,具有很好的适应性,而模糊免疫控制器无法对其进行有效的补偿,且由于非线性干扰造成的控制误差无法得到及时的修正[13],为此需要对参数进一步优化,过程如下所示:
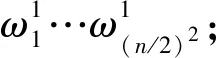
b.定义控制器的适应度函数[14],将其表示为
(7)
e(t)为第t个实数的调制参数;t为计算时间。
其中Q=I4,R=0.6。控制律取为状态反馈τ2=Kx,控制增益为K=-BTR-1P,其中P是下列Ricatti方程的解。
c.根据预先确定的标准对个体微粒的适配度函数进行评估。
d.对每个微粒寻找历史最好的位置,计算每个粒子的适应度函数均值,不断更新位置,表示为
(8)
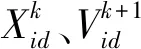
e.对当前条件判断,如果达到停止条件,则保留当前信息,返回当前适应度值。
f.通过上述迭代后,粒子群算法会逐渐收敛到最优解,作为伸缩因子的最优参数。
基于上述过程对PID控制参数优化[15],实时调节控制器,免疫 PID控制器的输出表示为
u(k)=u(k-1)+
KP1(e(k)-e(k-1))+e(k-2))
(9)
KP1为比例系数。
将自调整参数表示为
(10)
基于上述过程对参数优化,控制风力发电机励磁,风力发电机励磁控制流程如图2所示。
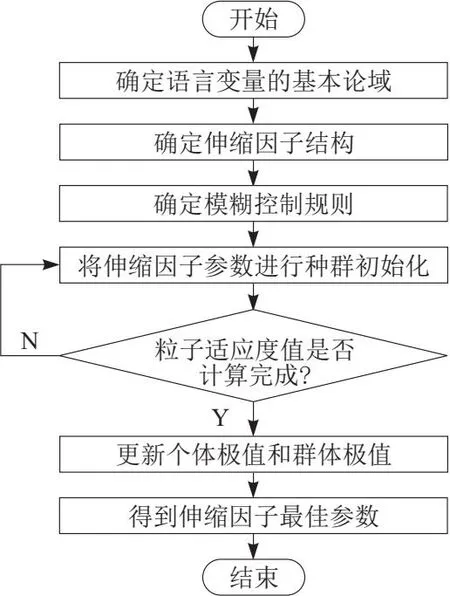
图2 风力发电机励磁控制流程
在实际应用中,通过调整比例因子,可以获得更好的动态和静态特性,增强了控制器的自适应能力。
3 实验对比
3.1 实验参数
为验证本文提出的基于模糊免疫自适应PID的风力发电机励磁控制方法在实际应用中的效果,选取某地区风力发电机为实验对象,如图3所示,进行仿真实验分析。

图3 实验对象
实验选取的风力发电机的参数设置如表1所示。
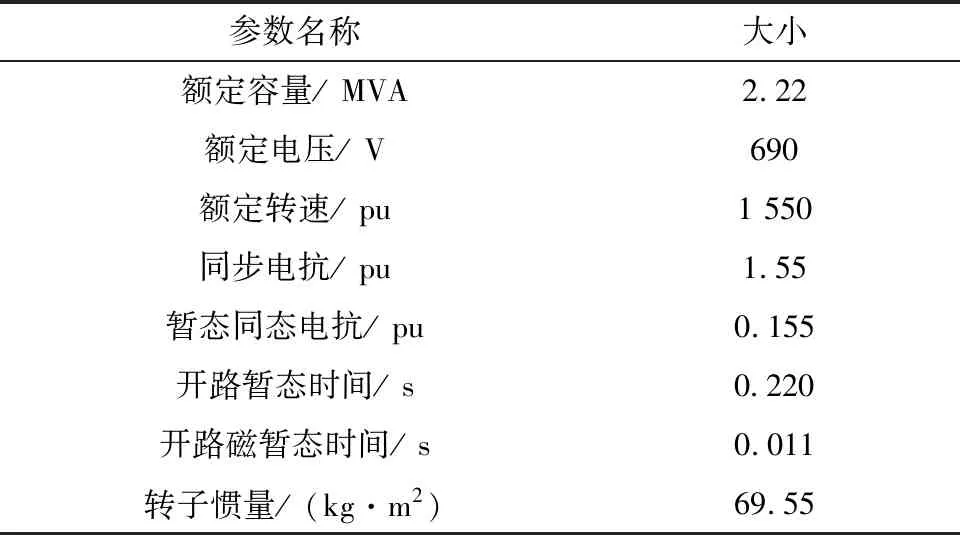
表1 发电机参数表
在实验过程中,采用取样电路对发电机的电压、电流等进行取样、调理,并将其进行相应的运算,最后由DSP进行处理。接着,DSP把所取样的信号与所述给定的信号进行比较,获得数据,并为了保证实验的严谨性,将文献[1]提出的基于模糊控制的方法、文献[2]提出的新型直驱交流励磁风力发电系统控制方法与本文提出的基于模糊免疫自适应PID的风力发电机励磁控制方法进行对比,比较3种方法的风力发电机励磁控制效果。
3.2 实验结果分析
预先对比发电机输出电压,结果如表2所示。
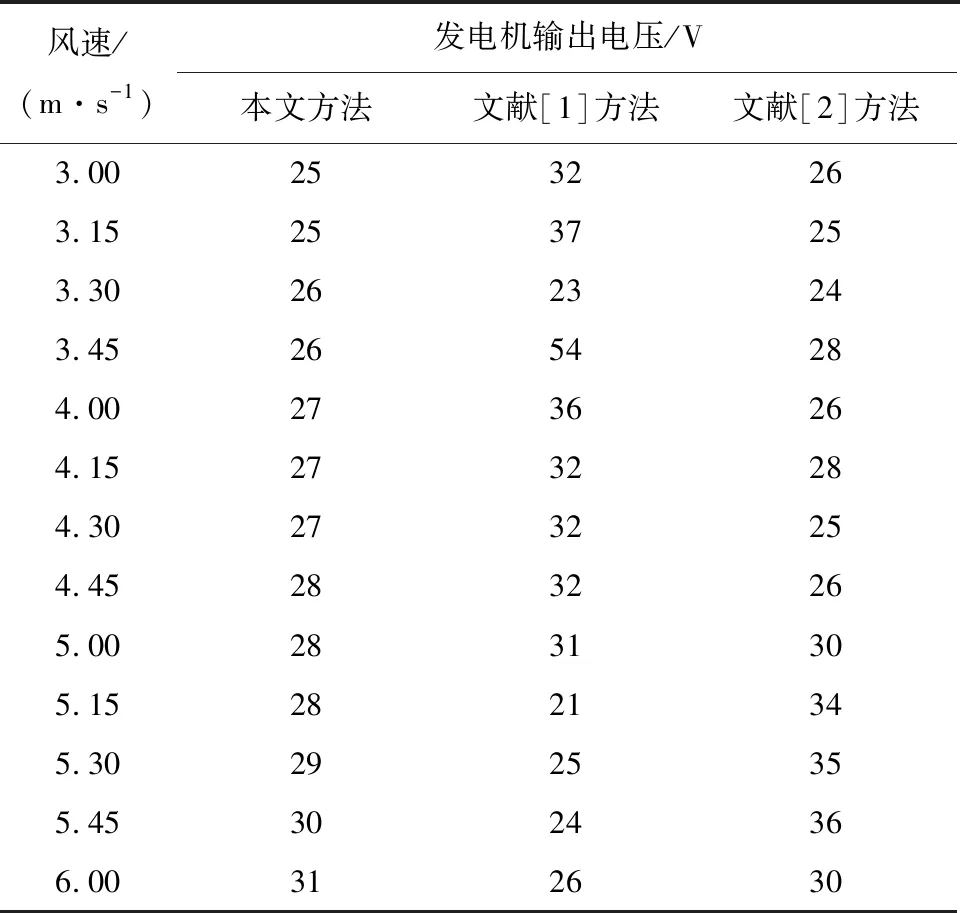
表2 发电机输出电压
由表2可知,本文方法的发电机输出电压能够达到输出电压恒定,符合并网的要求,较另外2种方法控制后效果好。
不同风速下励磁电压变化情况,结果如表3所示。

表3 励磁电压变化情况对比
由表3可知,本文方法进行风力发电机励磁控制后,随着风速增大电压逐渐减小,并且较为稳定,说明风力发电机励磁控制效果较好。另外2种方法虽然随着风速的变化而变化,但在风速增加后,电压变化情况不是很稳定。
接下来对比不同风速下,本文方法、文献[1]方法和文献[2]方法的励磁电流变化情况,对比结果如表4所示。
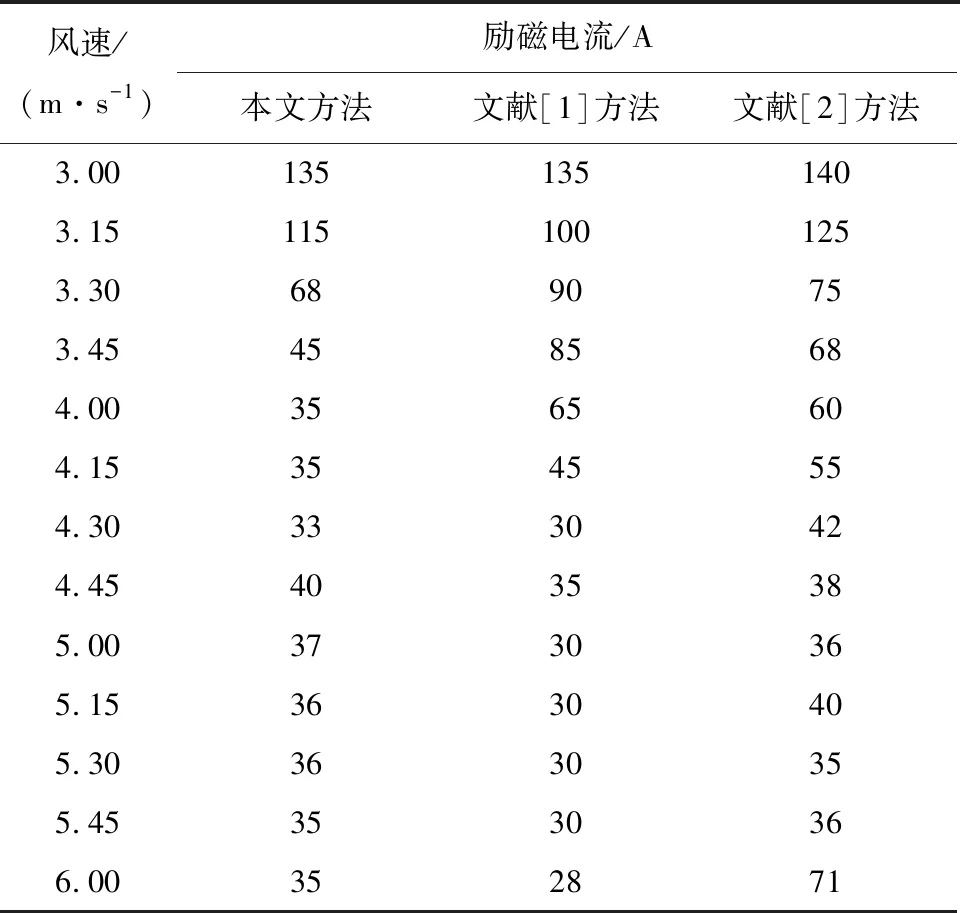
表4 励磁电流变化情况对比
由表4可知,当风速达到运行的最大风速区域时,本文方法控制后的励磁电流基本恒定,而文献[1]方法和文献[2]方法控制后,电流变化幅度较大,稳定性较差,说明控制效果没有本文方法的控制效果好。
接下来对比在外界风速一直处于额定风速时,本文方法、文献[1]方法和文献[2]方法的风力发电机组输出功率控制情况,3种方法的对比结果如图4所示。
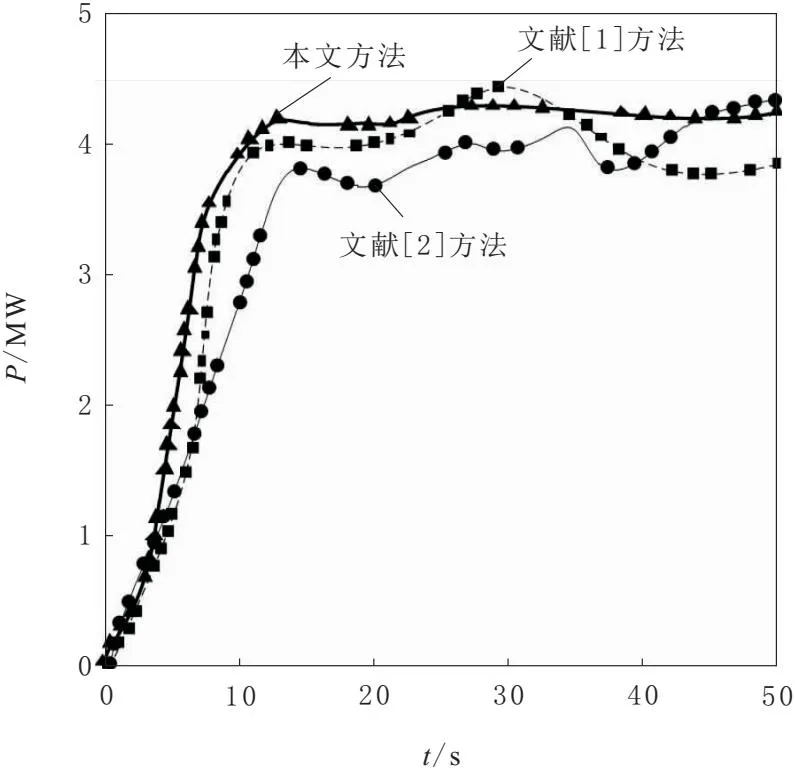
图4 系统输出功率曲线
由图4可知,在外界风速恒定的情况下,本文方法的风力发电机组输出功率控制调节作用较好,输出的功率基本恒定,能够实现对风能的最大利用,使整个风力发电系统稳定有效运行在有效风速情况下。而文献[1]方法和文献[2]方法的风力发电机组输出功率控制效果不是很理想,稳定性不是很好,具有较大的波动情况。
4 结束语
基于上述过程完成基于模糊免疫自适应PID的风力发电机励磁控制方法的研究,采用此方法对励磁系统调整,可以提高机组的风能利用率,使发电机的输出电压处于一个稳定的状态,从而保证其在最优的功率曲线以内,满足电网的并网需求。励磁技术在风电行业的应用尚处在起步阶段,本文在完成了一些工作的同时,也存在着一些问题,针对风电机组的无刷励磁系统,采用模糊控制与神经网络相结合的方法,目前尚处于模拟研究阶段,需深入探讨。
