城市年用水量聚类分析
2024-01-04李树平王莹莹唐之嵋王磊新陆纳新
李树平,王莹莹,唐之嵋,王磊新,陆纳新,姚 灵,陈 伟
(1.同济大学环境科学与工程学院,上海 200092;2.无锡市水务集团有限公司,江苏无锡 214031;3.宁波水表<集团>有限公司,浙江宁波 315032)
城市用水量既有周期性也有变化性。城市用水量周期性表现在一年、一周、1 d内的变化上(年用水量变化如图1所示)[1]。一年内用水量随不同季节的温度而变化;一周内分工作日和周末用水情况。当城市以居民活动为主导时,1 d内的小时用水量表现为“双峰双谷”特点(各地在如下所列时间上可能略有差异):早上5:00—6:00,人们开始准备一天的活动,用水量开始上升;到早上8:00—10:00达到最高峰;11:00—16:00用水量处于下降时段;16:00之后用水量又逐渐上升;20:00—22:00再次达到高峰;之后用水量逐渐下降;其中2:00—4:00为1 d内用水量最低时段,此时段的流量常称作夜间最小流量。

图1 某市365 d用水量变化Fig.1 365-Day Water Consumptions of a City
城市用水量变化性包括:(1)一年365 d(闰年366 d)并非一周7 d的整数倍,按照周规律变化时,并不能使不同年份的同一日历日固定为某周内的同一天;(2)每年农历日期与公历日期不是固定对应的,例如每年农历春节、端午节、中秋节等我国传统节日在公历中常常是变化的。此外,由于气候变化等原因,也会引起城市用水量的变化。
在城市用水量规律性分析中,分析一周内(工作日和周末)各日用水量变化、节假日用水量变化的文献居多;很少在一整年基础上,分析不同月份、不同日期之间用水的相似性和差异[2-6]。若能发现一年内不同日期之间用水的相似性,则可以初步根据先出现日期的用水规律,预测将要来临的相似用水特性日期的情况。同时,有助于总体掌握一年内的用水规律性。
为此,本研究将采用K均值聚类算法分析城市年用水量,试图寻找一年内不同日期之间用水的相似性和一年内的用水规律性,为城市用水量管理和供水运行调度提供有价值的信息。K均值聚类算法兼具模式识别和异常值诊断功能,已在供水用户类型识别中得到应用[7]。
1 K均值聚类算法
聚类是将样本中相似的数据点分配到相同的类,不相似的数据点分配到不同的类。聚类时样本通常是欧氏空间中的向量;类别不是事先给定,而是从数据中自动发现。样本之间的相似度或距离由应用决定[8]。
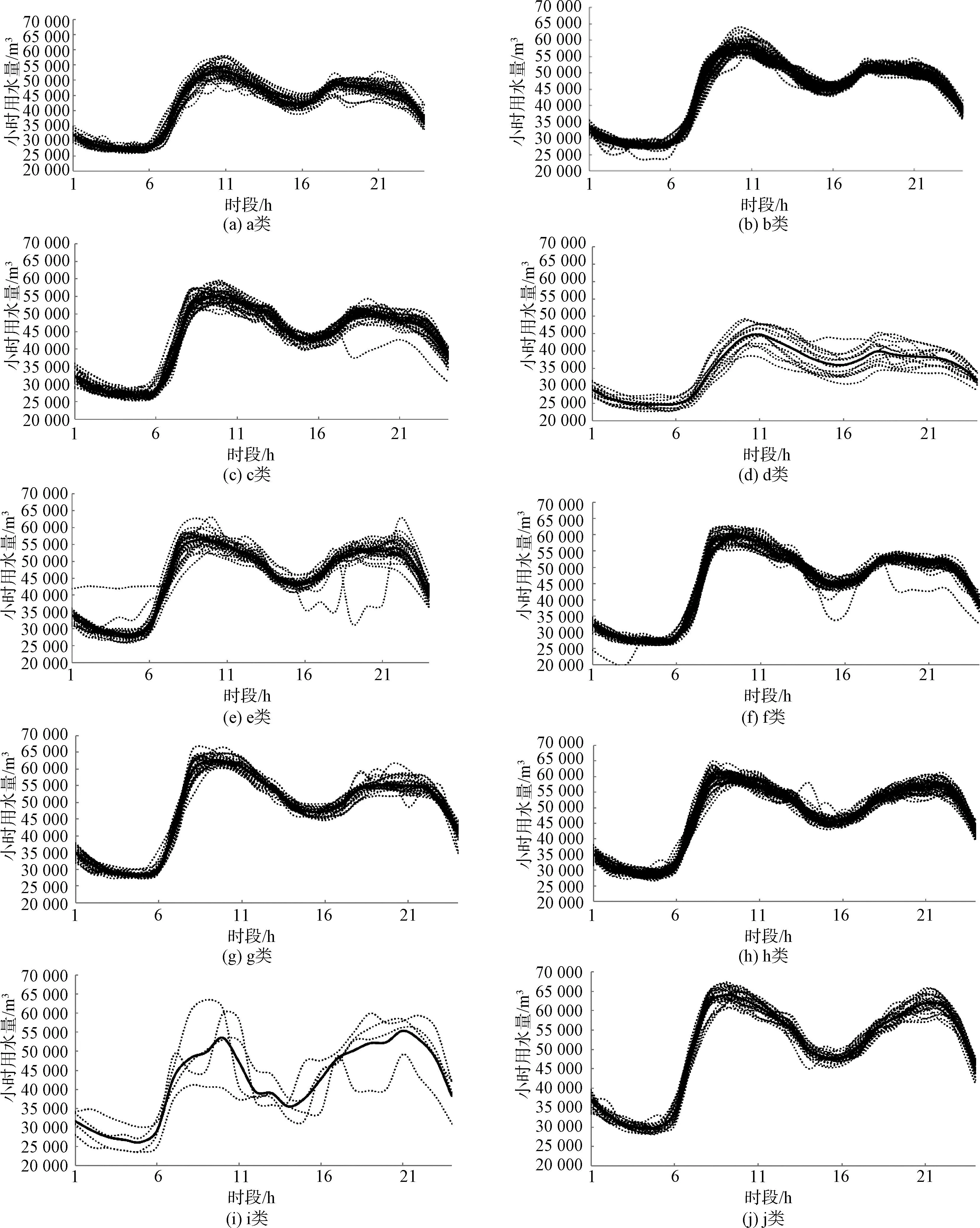
常用的K均值聚类算法将数据点集合划分为K个子集,构成K个类;将N个数据点分配到K个类别中(K (1) 输入N个数据点集X和类别数K。 (4) 计算各数据点到所属类别质心之间距离平方的总和(称作损失函数W(0))如式(1)。 (1) 其中:n(k)——类别k内所含数据点个数。 (2) (6) 计算新的损失函数W(1),即各数据点到所属类别质心之间距离平方的总和如式(3)。 (3) (7) 比较W(0)和W(1)的数值大小。如果W(1) K均值聚类算法受初始值和异常点影响,聚类结果可能不是全局最优而是局部最优。(1)尽管异常点会影响聚类结果,但K均值聚类算法的一个优点就是可用于检测异常值。因此,当检测到异常值时,对其进行修正,重新执行计算,将会克服异常值的影响。(2)选择不同的各类质心初始值会得到不同的聚类结果。通常需要执行多次运算,从中选择可使相应损失函数较小的分类结果作为最终聚类结果。 以上K均值聚类中的类别数K值需要预先指定,而实际应用中最优K值是不知道的。K值的选择常采用手肘法:尝试不同K值并将对应的损失函数绘制成曲线图;随着K值增大,经过图中曲线拐点后损失函数将不再显著变化,因此,认为该曲线拐点就是所求最优K值[10]。 K均值聚类算法的应用还包括前期原始数据的预处理,以及计算结果的分析。 算例采用我国华东某城市365 d逐时用水量进行分析。在该365 d内最低小时用水量为20 000 m3,最高小时用水量为67 227 m3。算例分析之前需先对异常值进行处理。 一年内每日的小时用水量原始数据中可能存在异常值,在本研究算例中异常值包括小时用水量为0或较低值。经与现场工作人员了解,很少出现小时用水量的超高值异常,因此,本研究中未考虑超高值异常。小时用水量为0时很容易辨识出来;而大于0的较低值隐藏在大量数据之内,很难辨识,通常需要在K均值聚类分析后发现。 用水量常会出现逐小时用水量高低变化的情况,线性插值法处理会抹去中间点的上凸或下凹特征,因此,不能按照线性插值处理。针对某小时用水量异常值的修正,可引入权重系数,将前1 h和后1 h数据,以及前1 d和后1 d该小时数据处理为式(4)。 (4) 其中:w1、w2——权重,数值均在[0,1],且w1+w2=1,应根据相邻数据变化趋势确定; Qij——第id第jh的用水量,m3; Qi-1,j、Qi+1,j——第i-1 d第jh、第i+1 d第jh的用水量,m3; Qi, j-1、Qi, j+1——第id第j-1 h、第j+1 h的用水量,m3。 在K均值聚类分析中,数据点总数N取365;数据点xi=(xi1,xi2,…,xih,…,xiH)为H=24的向量,由1 d内24 h用水量组成。 针对K= 1,2,…,20,分别执行K均值聚类计算,将不同K值获得的损失函数值绘制成曲线(图2)。为使聚类具有充分代表性,参考手肘法,取K= 10作为该年每日用水量聚类的类别数,各类别分别记为a,b,…,j(图3、表1)。各类别质心数据如图4所示。以下分别从逐月、逐类别和季节性方面进行说明。 图2 不同K值对应损失函数值Fig.2 Loss Function Values Corresponding to Different K Values 注:图中实线为该类别平均用水量,虚线为具体日期用水量变化。 图4 各类别质心小时用水量Fig.4 Hourly Water Flow of Centroid of Each Cluster 表1中逐月与各个类别的对应情况如下。该年度1月用水可归为4类,主要为a类(13 d)和b类(13 d)。2月用水可归为5类,主要为a类(15 d)和d类(9 d)。3月用水可归为5类,主要为b类(10 d)和c类(12 d)。4月用水可归为4类,主要为a类(7 d)、c类(12 d)和f类(10 d)。5月用水可归为8类,主要为e类(9 d)。6月用水可归为5类,主要为e类(9 d)和h类(17 d)。7月用水可归为4类,主要为e类(7 d)、h类(8 d)和j类(14 d)。 8月用水可归为5类,主要为h类(17 d)和j类(8 d)。9月用水可归为5类,主要为g类(8 d)和h类(14 d)。10月用水可归为4类,主要为f类(8 d)和g类(18 d)。11月用水可归为4类,主要为b类(7 d)和f类(19 d);12月用水可归为3类,主要为b类(25 d)。其中,归类数最少的为12月(3类),最多的为5月(8类)。 表1中逐个类别与日期对应情况如下。a类共含43 d用水量数据,多数为1月(13 d)、2月(15 d)用水,所含4月用水量(7 d)均处于周末(星期六和星期日);a类中含有元旦、元宵节、端午节3个法定假日。b类共含57 d用水量数据,多数为12月(25 d)、1月(13 d)和3月(10 d)用水量。c类共含43 d用水量数据,多数为3月(12 d)、4月(12 d)用水量;c类中含有清明节、劳动节和国庆节3个法定假日;含有5月1日—4日,10月1日—4日的用水量。d类共含有连续从1月28日—2月9日13 d的用水量数据,其中2月1日春节。e类共含36 d用水量数据,多数为5月(9 d)、6月(9 d)、7月(7 d)用水量。f类共含50 d用水量数据,多数为4月(10 d)、10月(8 d)、11月(19 d)用水量。g类共含31 d用水量数据,多数为9月(8 d)、10月(18 d)用水量。h类共含61 d用水量数据,多数为6月(17 d)、7月(8 d)、8月(17 d)、9月(14 d)用水量。i类共含5月(2 d)、6月(1 d)、8月(1 d)的数据,从图4中可以看出,1 d内水量变化趋势极不稳定。j类共含27 d用水量数据,多数为7月(14 d)、8月(8 d)用水量。 逐个类别对应季节性情况为:a类和b类反映了冬季用水;c类反映了春季用水,且含有“五一”和“十一”两个小长假期间的用水;d类为春节前后用水;e类、h类和j类反映了夏季用水;g类反映了秋季用水;f类反映了春末和初冬用水。由图3可知,d类(春节前后)各小时用水量均较低;j类(7月、8月)各小时用水量均较高。 城市年用水量的周期性和变化特征可采用K均值聚类算法进行理论分析。K均值聚类算法具有模式识别和异常值诊断功能,在使用中应关注各类质心初始值的随机选取问题,以及K值非预先指定特点,需要多次运行,以获得最优K值和较小损失函数结果。 以华东某城市某年逐日用水量为原始数据,分析认为K=10较为合理;分类中的明显特点包括用水高峰作为一类,春节期间用水量较少时作为一类,“五一”和“十一”小长假期间用水作为一类。 在小时用水量异常值处理中,为兼顾时用水变化中上凸和下凹特点,考虑利用前后两日该时段用水量和前后2 h用水量的加权方式修正。 本研究只针对一年的用水量进行了计算,如果每年能够采用K均值聚类算法分析,充分考虑特殊年份用水(例如出现冬季冻灾、受新冠疫情影响等),将会对城市用水量管理和供水运行调度提供更有价值的信息。

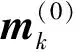
2 算例分析
2.1 异常值处理
2.2 K均值聚类分析


3 结束语
