微型涡流发生器对空化初生特性的影响

龚瑜璠,胡常莉,洪伯杰,杨斯睿,纪潇曈

(南京理工大学 能源与动力工程学院, 南京 210094)

0 引言

空化是指当液体内部的局部压力降低到饱和蒸汽压力以下时,液体内部或固液交界面上蒸汽或气体的空泡形成、发展和溃灭过程。在高速水中兵器[1]、水下航行体[2]、舰船[3]及两栖车[4]螺旋桨叶片表面空化现象时常发生,对其安全运行造成了严重影响。空泡的脱落和溃灭会引发不同程度的振动和噪声[5-6],影响到船员的舒适性和舰船的隐蔽性。长期的空化会加剧叶片表面的侵蚀破坏,缩短其使用寿命[7],同时也对弹体及水下航行器的运动状态和稳定性造成影响[8-9]。空化初生是空化的最初阶段,开展初生空化流动控制方法的研究具有十分重要的工程价值和科学意义。

20世纪70年代,大量研究发现边界层分离是诱导空化的重要原因之一,层流边界层分离与空化初生之间存在很强的相关性。Arakeri等[10-11]用纹影成像的方法证明了层流边界层分离存在于空化脱离点上游。Joseph[12]发现空化起始区位于转捩区下游的湍流剪切层或具有较大分离区物体的再附着区上游,且与混合层涡旋结构有关。Franc[13]通过实验发现附着空化与边界层之间存在着强烈的相互作用,并且当对翼型攻角稍作调整后,使得流动转捩为湍流,流动分离不再发生,此时附着空化会瞬间消失。可以从前人的这些研究中得到启示:通过人为地激发流动转捩湍流来消除层流分离,可以抑制在某些情况下所形成的附着空化。

由于边界层状态会对空化的形成发展产生显著影响,故近年来许多学者通过采用被动控制的方法来控制边界层,进而控制空化。Lin等[14]研究了不同尺寸的弧形障碍物对空化演化的影响,发现障碍物对平板水翼空化脱落频率和含气量分布均有影响,可以稳定前缘空腔,减小脱落空腔的尺寸。Zhang等[15]发现障碍物的存在改变了瞬态回射流的强度和方向,以及空腔尾部的压力分布,导致云空化的脱落变弱。Chen等[16]利用前缘粗糙度改变了前缘区域的局部压力分布,显著提高了最小压力系数,从而降低了水翼的初生空化数,延缓空化起始时间。在众多被动控制方法中,微型涡流发生器对边界层分离有很好的控制效果,有着尺寸小、成本低且高效等优势,在空气动力学领域已经有相当成熟的应用,能起到很好的增升减阻效果[17-18]。近年来,研究人员将微型涡流发生器引入到水动力领域来对空化流动进行控制,并取得了一定的成果。Javadi等[19]引入了人工空泡发生器(ACG)的概念,发现在ACG的后部会形成一个低压回流区,且当ACG的形状、位置、大小合适时,该区域液体的局部静压始终低于饱和蒸汽压,人为地产生了静止的空泡,能够很好地控制空化过程。车邦祥等[20]在水翼前缘安装微型涡流发生器(MVG)来控制流动分离,发现MVG所诱发的稳定对漩涡和涡空化结构,对近壁面流动具有整流作用,使得空泡脱落过程呈现显著的周期性,从而实现了对水翼附着空化的形成和稳定性控制。Kundu等[21]利用涡流发生器(VGs)来提升水翼性能,发现与同向旋转的VGs相比,反向旋转的VGs能够更加显著提高水翼升阻比,且当VGs逐渐向后缘移动时,失速角增大,峰值升力系数增加。Kadivar等[22-23]将圆柱形微型涡发生器安装在CAV2003水翼表面后,发现大尺度云空化得到了缓解,只有小尺度的空泡结构从水翼表面脱落,并且水翼尾流区的压力脉动也明显减小。Qiu等[24]发现在水翼前缘安装MVG后能够形成稳定的涡流管,从时间和空间上分散了空泡云的集中坍塌,大幅减小空泡脱落时对水翼的撞击能量和对水翼前缘的冲蚀,尤其在小攻角时,缓解作用更为突出。Li等[25]设计了一种三角形涡流发生器并安装在船艉的表面,使得尾迹的周向过渡变得更加缓和,增大了叶片空化坍塌位置与船底壳体之间的距离,有利于降低脉动压力的幅值,减小振动。

综上所述,现有涡流发生器对控制空化方面的研究主要集中于云空化阶段,而对空化初生控制的相关研究较少。因此,本文将采用数值计算的方法研究MVG对不同攻角条件下绕NACA66水翼流动分离和初生空化特性的影响机制,以期为工程实际中抑制空化初生的方法研究提供理论支撑。

1 数值计算模型和方法

1.1 数值计算模型

采用均相流模型,气液两相的连续性方程和动量方程为

(1)

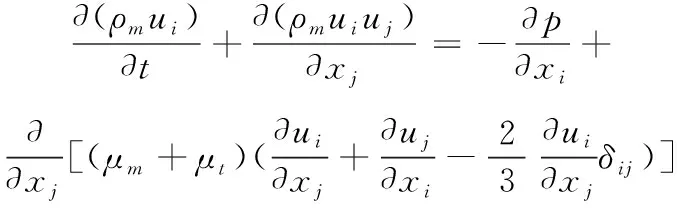
(2)

混合相密度和黏度为

ρm=ρlαl+ρvαv

(3)

μm=μlαl+μvαv

(4)

式(3)—式(4)中:下标i和j表示坐标方向;u和p分别表示混合相速度和压力;ρm、μm、μt分别是混合相密度和混合相层流/湍流黏性系数;α代表体积分数;下标l和v分别表示液相和气相。

湍流模型采用的是SSTγ-Reθt模型。它由Langtry等[26]提出,是在SSTk-ω基础上增加了2个输运方程,一个为计算间歇性,另一个为计算转捩起始。其中,间歇因子γ运输方程

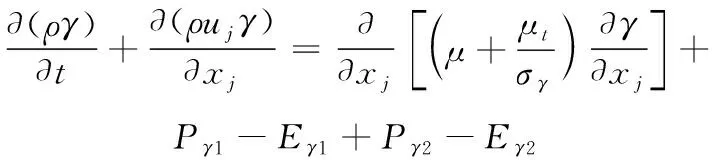
(5)

Pγ1=FlengthρS[γFonset]ca1

(6)

Eγ1=ce1Pγ1γ

(7)

Pγ2=ca2ρΩγFturb

(8)

Eγ2=ce2Pγ2γ

(9)

其中:S为应变率;Flength是用来调节转捩区长度的参数;Ω为涡量;Fturb的作用是在层流边界层外或黏性底层内使破坏项Eγ不起作用。与其他间歇模型的主要区别在于Fonset是涡量雷诺数Rev的函数,用来触发间歇因子生成项Pγ。

过渡动量厚度雷诺数的运输方程为

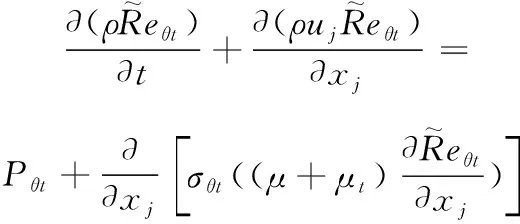
(10)

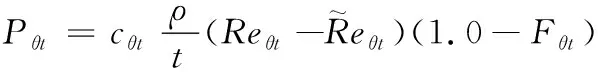
(11)

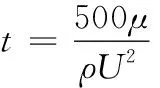
(12)

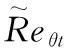
转捩模型与原始SSTk-ω湍流模型耦合得到的SSTγ-Reθt模型为

(13)

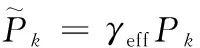
(14)

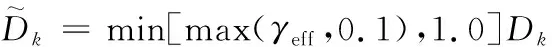
(15)

(16)

F3=e-(Ry/120)8

(17)

F1=max(Florig,F3)

(18)

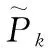
空化模型采用的是Zwart空化模型[27],该模型已被广泛地应用于水翼空化的模拟[28-29],且计算结果能够较好地与实验结果相吻合。Zwart空化模型的输运方程为:

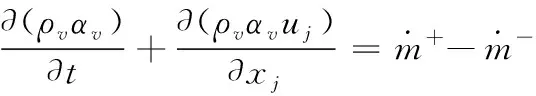
(19)

考虑到随着气体体积分数的增加,气核密度减小。为了使模型同时适用于气泡溃灭消失过程和生长过程,在气化过程中用rnuc(1-rv)代替rv,rnuc表示气核体积分数,rv表示气泡体积分数。RB为气核半径。空化模型的最终形式为

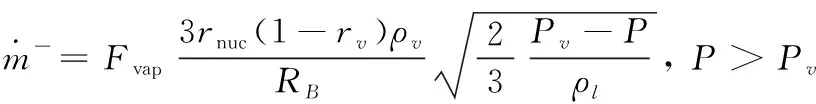
(20)

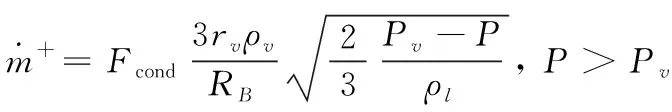
(21)

式(20)—式(21)中,各系数取值为RB=2×10-6m,rnuc=2×10-6m,Fvap=50,Fcond=0.01。

1.2 无量纲参数

本文中所涉及的无量纲参数主要有雷诺数Re、空化数σ、压力系数Cp、升力系数CL、阻力系数CD等,其定义分别为

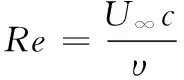
(22)

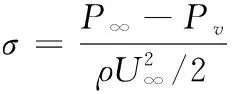
(23)

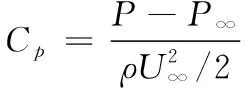
(23)

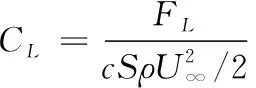
(24)

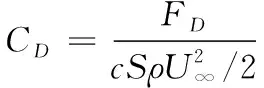
(24)

其中:P∞为环境压强;ρ为水的密度;ν为水的运动学黏度;U∞为来流速度;c为水翼弦长;S为水翼展长;FL和FD分别为水翼所受升力和阻力。

1.3 计算域设置与网格划分

以NACA66水翼为研究对象,其弦长c=0.07 m,展长S=0.001 m。微型涡流发生器的形状为三角形,如图1所示,长度lMVG=0.057c,高度hMVG=0.001 4c,距离水翼前缘xMVG=0.286c。

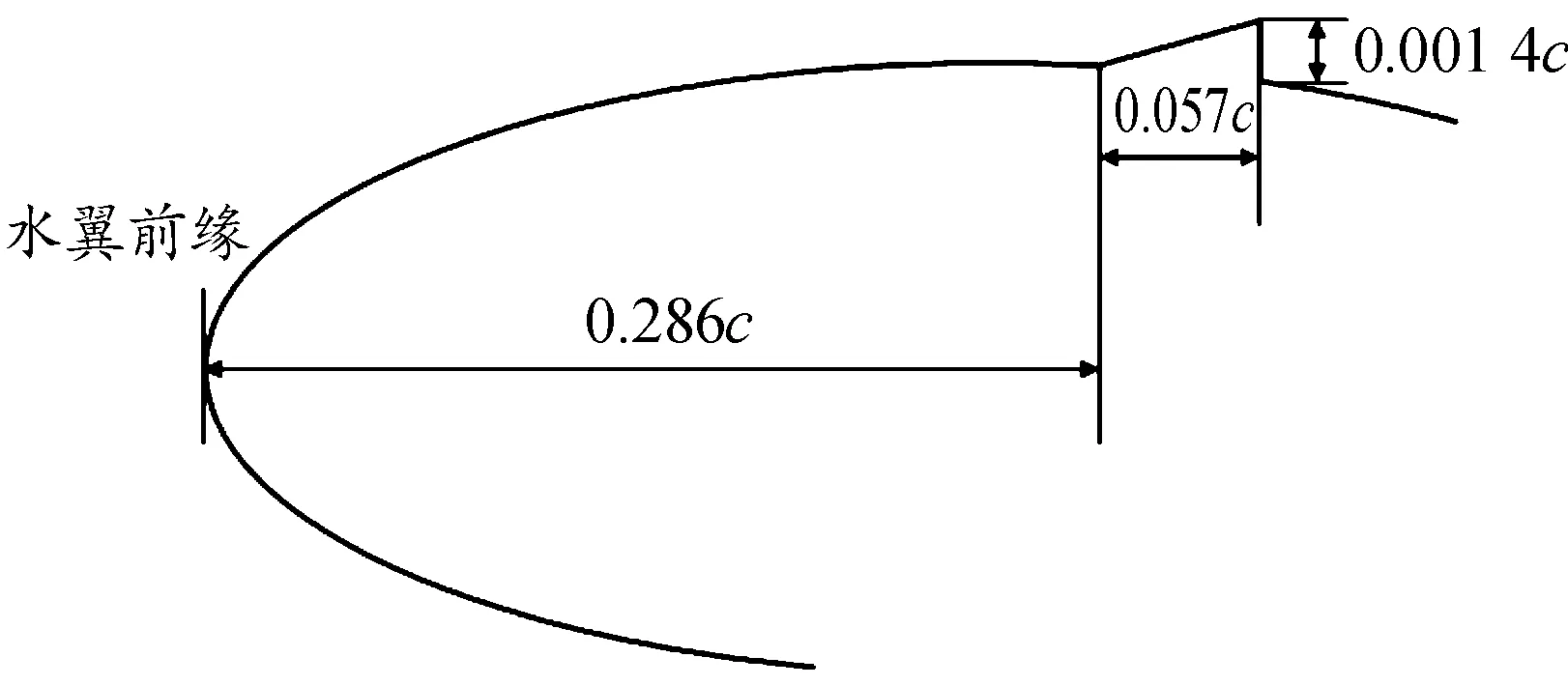
图1 MVG几何尺寸与弦向位置

数值计算基于ANSYS CFX仿真软件,计算域和边界条件的设置如图2所示,入口处为速度边界,流速为U∞=10 m/s,对应的雷诺数Re=7.8×105,出口为开放式压力边界,压力通过改变空化数来调节,流动区域的前后2个端面为对称边界条件,上下壁面为自由滑移壁面,水翼表面以及MVG的表面设置为无滑移壁面。

由于在不同攻角下流动分离区的位置不同,首先在攻角为4°、6°和8° 3个工况下,计算得到无MVG水翼流动分离点和再附着点位置,分别为0.464～0.519c,0.264～0.302c和0.235～0.275c。然后将MVG安装在距离水翼前缘x=0.286c处,这样就使得4°攻角时MVG位于流动分离涡之前,6°攻角时位于流动分离涡内,8°攻角时位于流动分离涡之后,如图3所示,以此实现通过调整攻角来改变MVG与流动分离涡相对位置的目的。

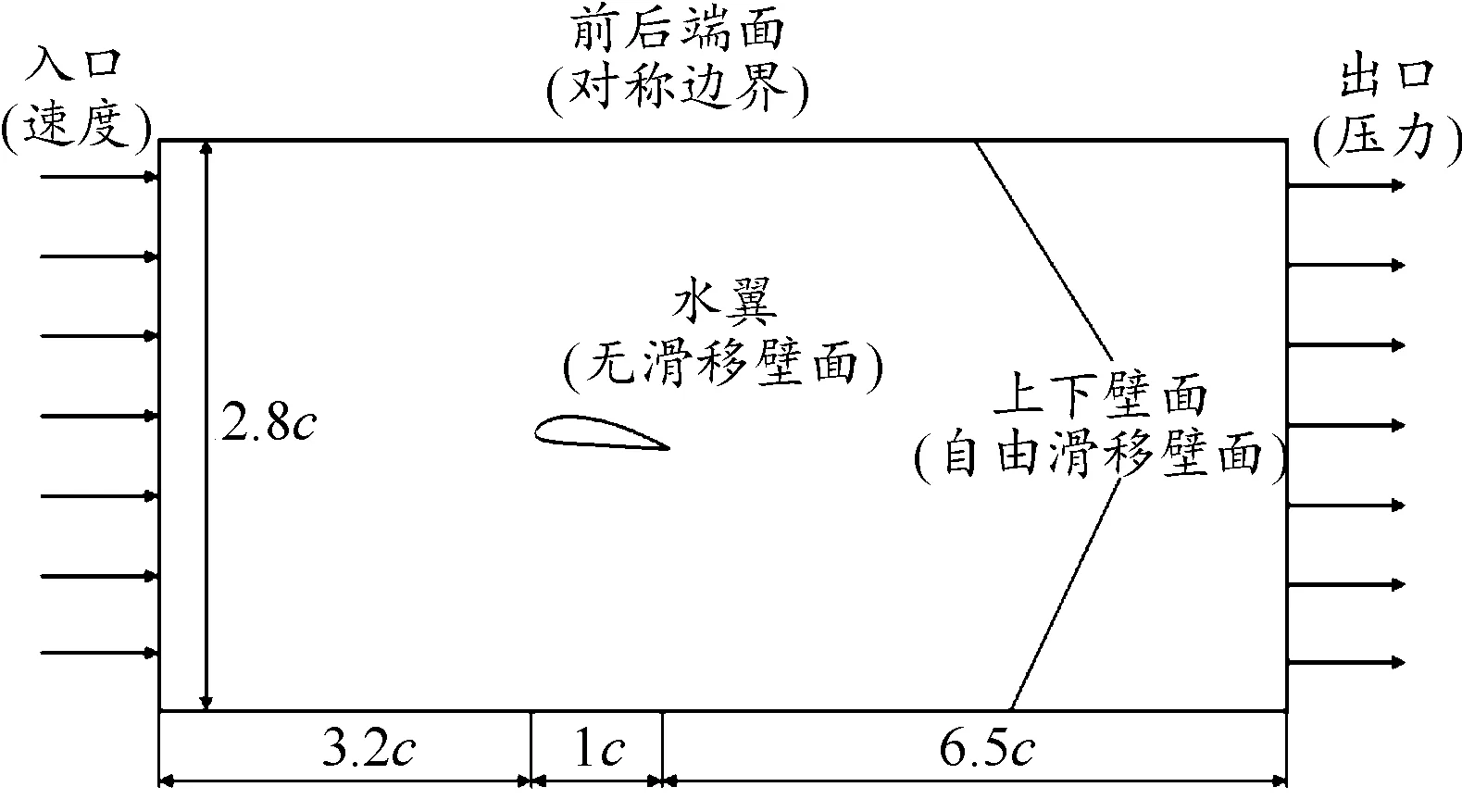
图2 计算域与边界条件

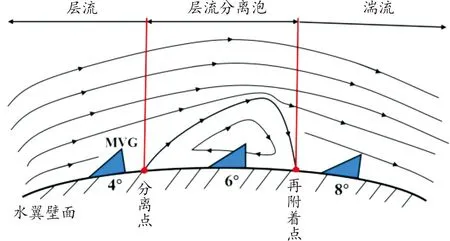
图3 不同攻角下MVG相对于无MVG水翼 流动分离涡的位置

图4展示了水翼和MVG附近的网格划分情况。计算域采用结构化网格,并对水翼壁面和涡流发生器区域的网格进行加密处理,为了排除网格数对计算结果的影响,首先进行了网格无关性分析,图5给出了采用不同网格数所计算出的时均升力系数,可见当网格加密到86万后,升力系数趋于稳定。从计算的准确性和经济性出发,选用了节点数为86万的网格进行水翼初生空化流动的数值计算。

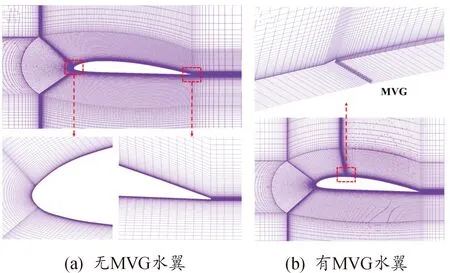
图4 网格划分Fig.4 Mesh subdivision

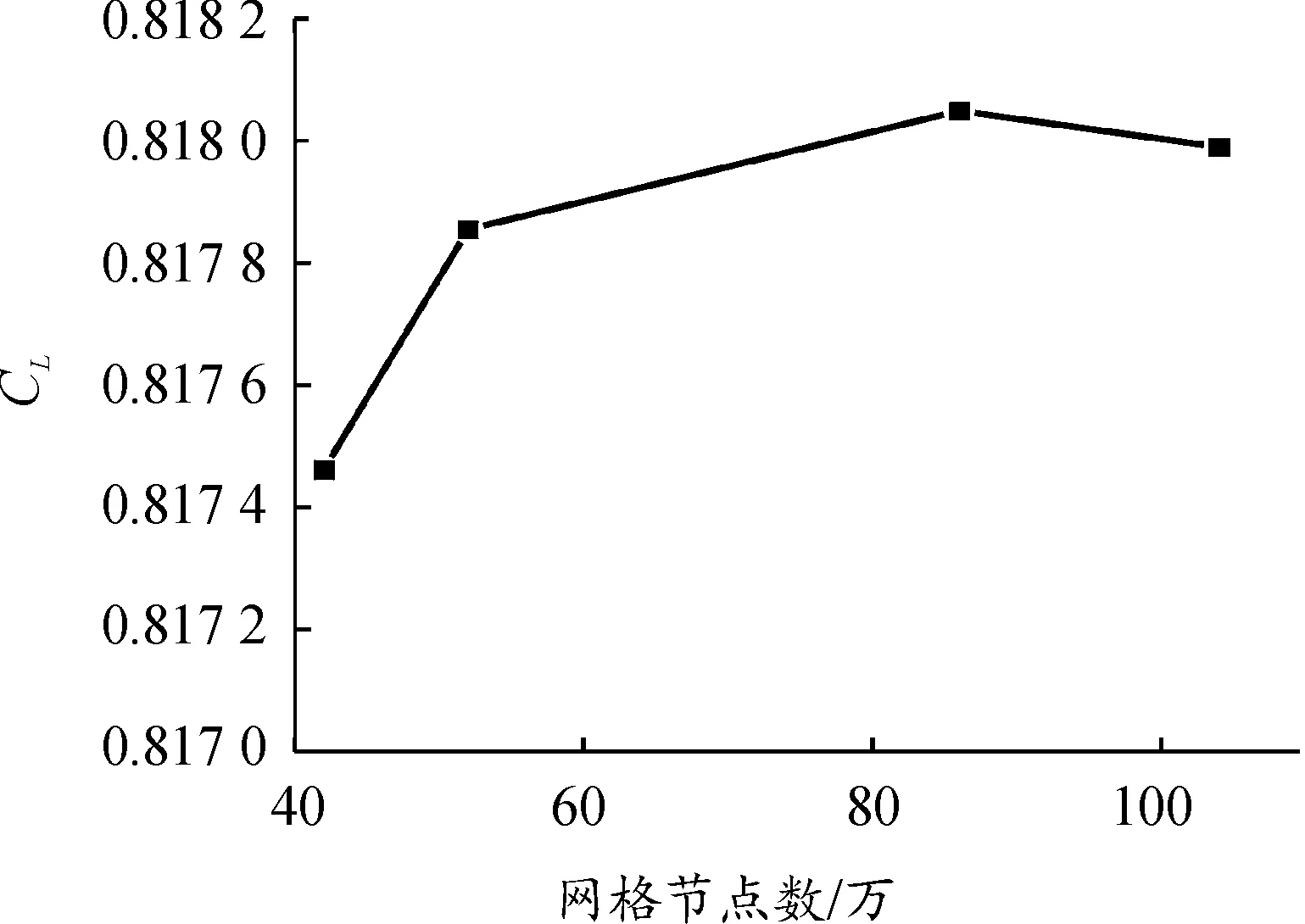
图5 不同网格计算得到的时均升力系数

1.4 数值模型的验证

采用与实验[30]相同的工况,在8°攻角,空化数为0.8的条件下进行计算。表1为实验及其他数值模型计算得到时均升阻力系数,从表1中可以看出,本文中所采用的数值模型对时均升阻力系数的预测与实验数据相比均偏低,但与其他数值模型的计算结果都比较接近。图6为水翼瞬时升力系数的模拟值和实验数据之间的比较,可见升力系数在时间上的周期性波动。

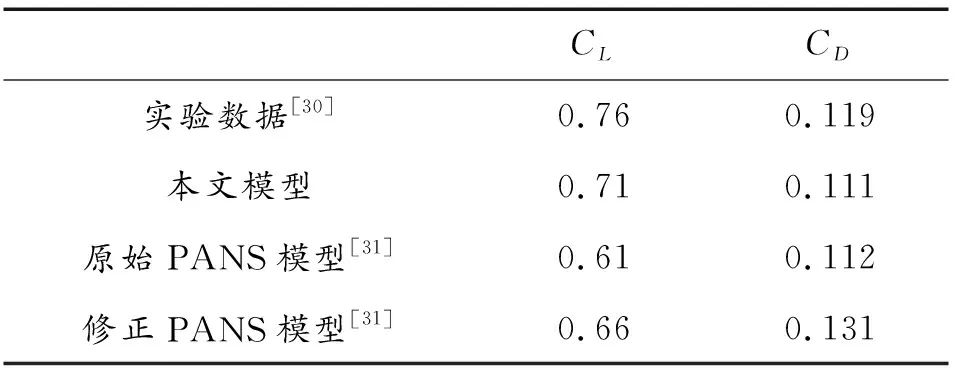
表1 不同数值模型下的时均升阻力系数对比

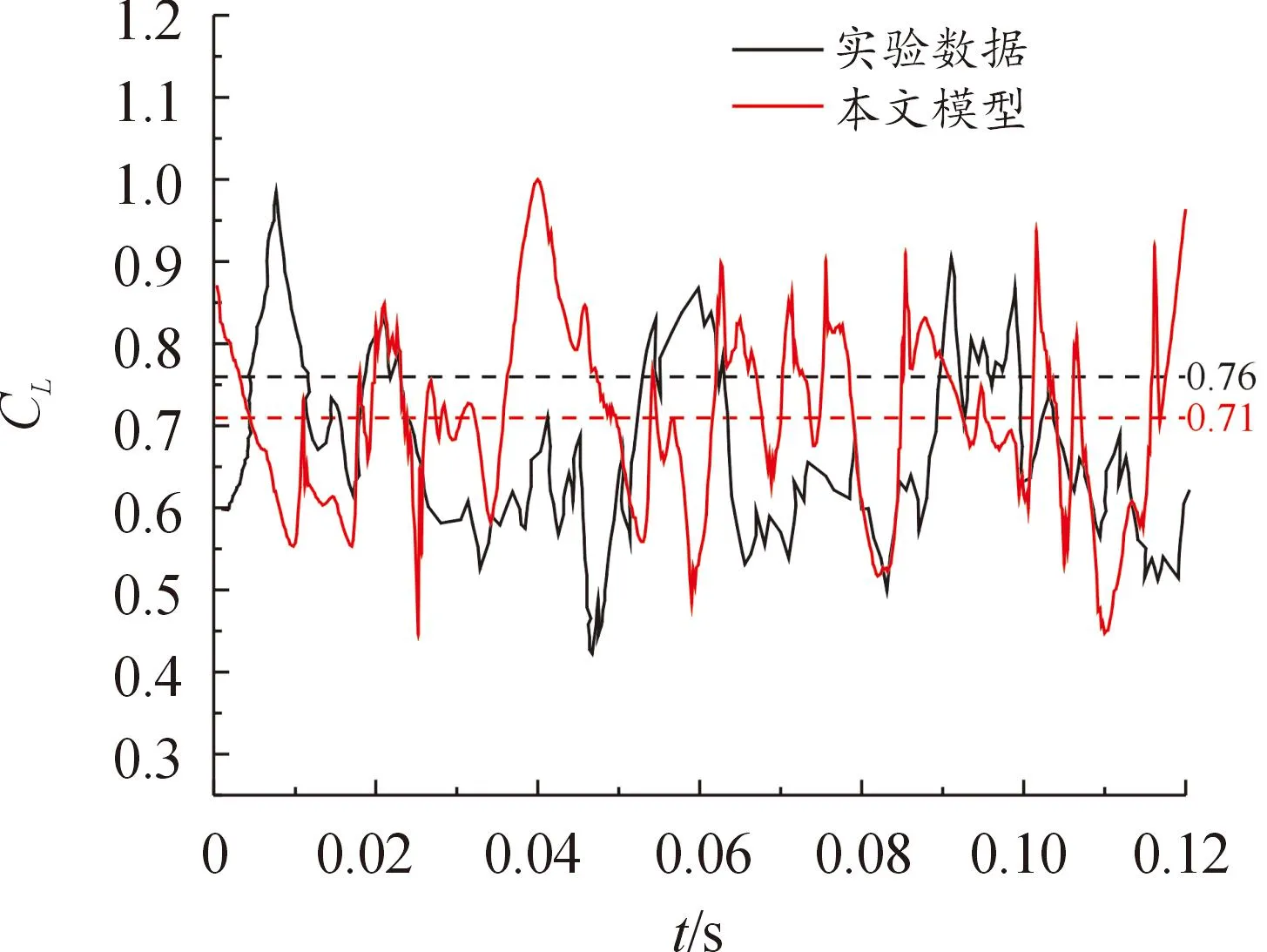
图6 水翼升力系数的时间变化

SSTγ-Reθt模型广泛应用于边界层自然转捩和分离转捩的预测,对边界层厚度和水翼尾迹区流动参数的预测与实验结果吻合良好[32]。本文中4°攻角时无MVG水翼的分离涡位于水翼的中部(0.464～0.519c),6°攻角以后,分离涡移动到水翼前缘,且随着攻角增大,分离涡逐渐向水翼前缘发展。这与文献[33]和[34]中的实验和数值结果相吻合,也证明了该数值模型在所计算的工况下具有较好的准确性。

2 结果的分析与讨论

2.1 微型涡流发生器对流动分离的影响

边界层流动特性对初生空化具有十分重要的影响,为了得到MVG附近当地边界层厚度,在水翼展向中间截面设置了如图7所示的4条检测线来提取局部速度分布,y为检测线上的坐标值,当地速度以无量纲形式U/U∞表示,即当地速度与来流速度之比。从图8所示的速度剖面来看,在所计算的攻角范围内,检测线处的边界层厚度约为0.25±0.02 mm,随着攻角的增大,4个位置的边界层厚度都略微增大,这与实际经验相符合,并且高度为0.1 mm的MVG始终在边界层厚度之内,意味着MVG能对边界层内的速度产生影响,并且安装MVG后,MVG后端边界层厚度增大。

图9给出了不同攻角条下有、无MVG水翼吸力面速度分布,从其中可以看出,无MVG水翼的速度分布在3个攻角下都呈现出相同的变化趋势,水翼表面流速先沿弦向逐渐减小,出现层流分离泡,随后转捩为湍流后重新附着在壁面上,此时流速急剧上升达到峰值后慢慢下降。对安装了MVG的水翼,MVG下游处的分离涡促进了主流区与近壁面流体的相互混合和质量交换,使得MVG下游处的流速大幅提高,如图9(a)所示。其中4°攻角时流速的增幅最大,消除了图9中Ⅳ区域的流动分离现象。

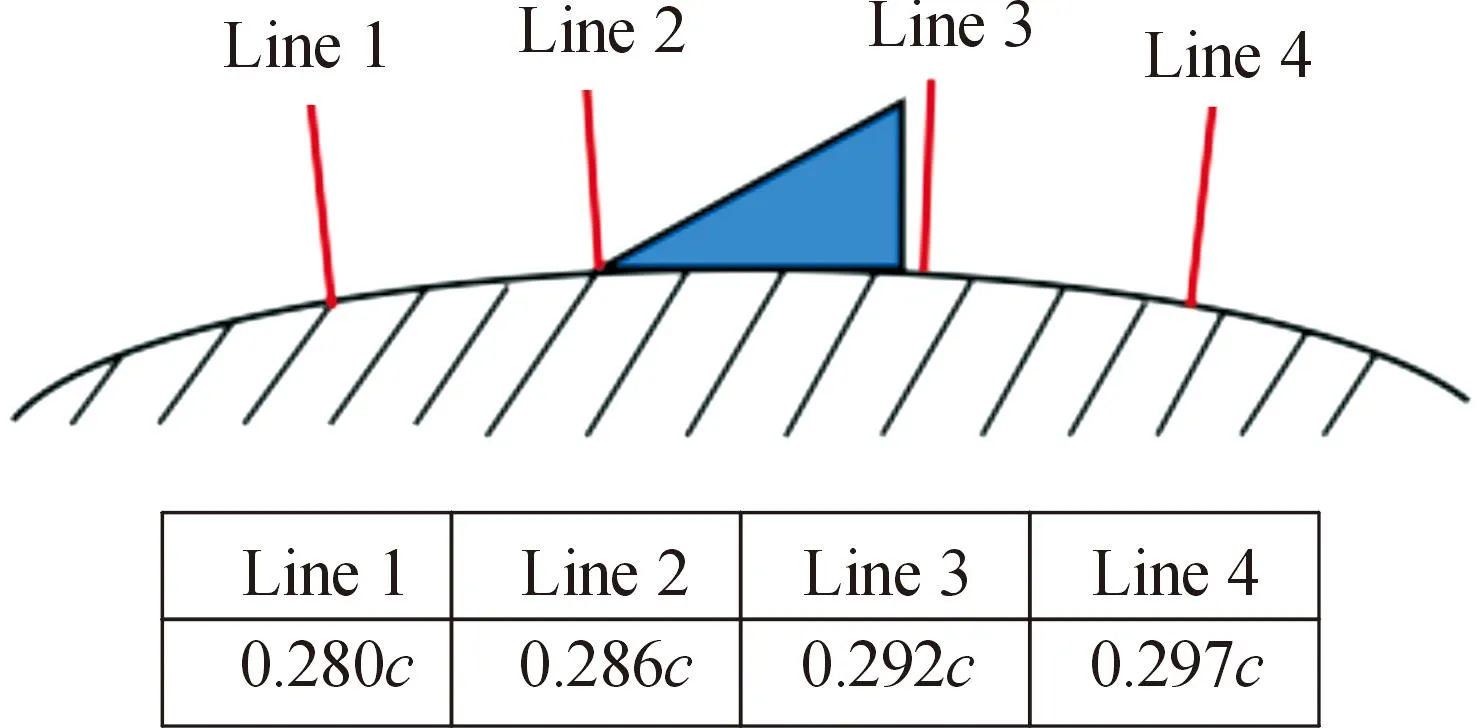
图7 MVG附近检测线位置

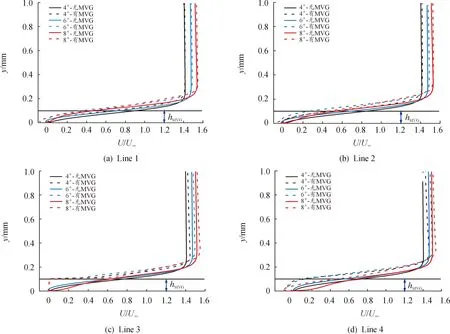
图8 有、无MVG水翼各检测线处速度分布

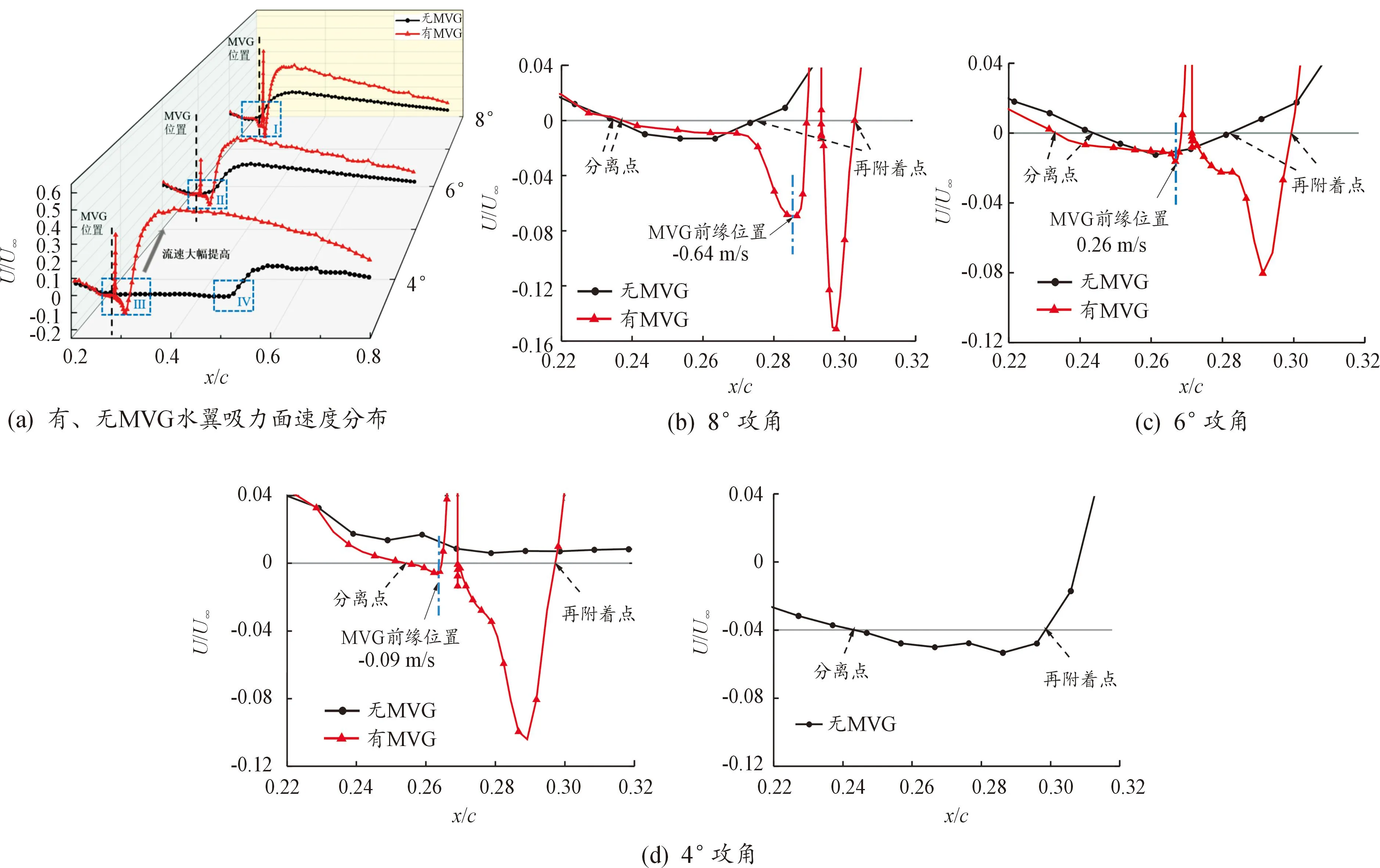
图9 不同攻角条下有、无MVG水翼吸力面速度分布及局部放大视图

图10给出了各攻角下MVG附近流线,从图10中可以看出,在MVG前后会分别产生漩涡结构,且分离涡被固定在该区域。随着攻角增大,MVG前端的漩涡结构更加明显,而其产生的反向射流可能对分离点的位置产生影响。结合图9的速度分布可知,当水翼攻角分别为4°、6°和8°时,位于MVG前端的反向速度分别是-0.09、-0.26、-0.64 m/s,攻角越大,反向射流速度越大。为了更好地分析MVG对流动分离的影响情况,表2统计了不同工况水翼的流动分离点和再附着点位置。图11给出了不同攻角下有、无MVG水翼分离涡的位置和尺度,从图11中可以看出,随着攻角增大,流动分离涡的位置向水翼前缘移动。与无MVG水翼相比,在安装MVG后,4°攻角时MVG位于流动分离涡之前,基础水翼中部的流动分离被抑制,而从MVG前端开始发生分离,如图10(a)所示,使得分离点和再附着点提前,但MVG前端的反向流速较小,能够向上传播的距离短,分离涡尺度减小;6°攻角时MVG位于流动分离涡内,MVG促进了漩涡的产生,其前缘的反向流速增大,使得分离点提前,再附着点延迟,分离涡尺度增大;8°攻角时MVG位于流动分离涡之后,分离点位置基本不变,而MVG前端形成的反向射流速度较大,向上传播发展与分离涡相混合,使得流动分离继续向下发展,再附着点延迟,分离涡尺度增大。

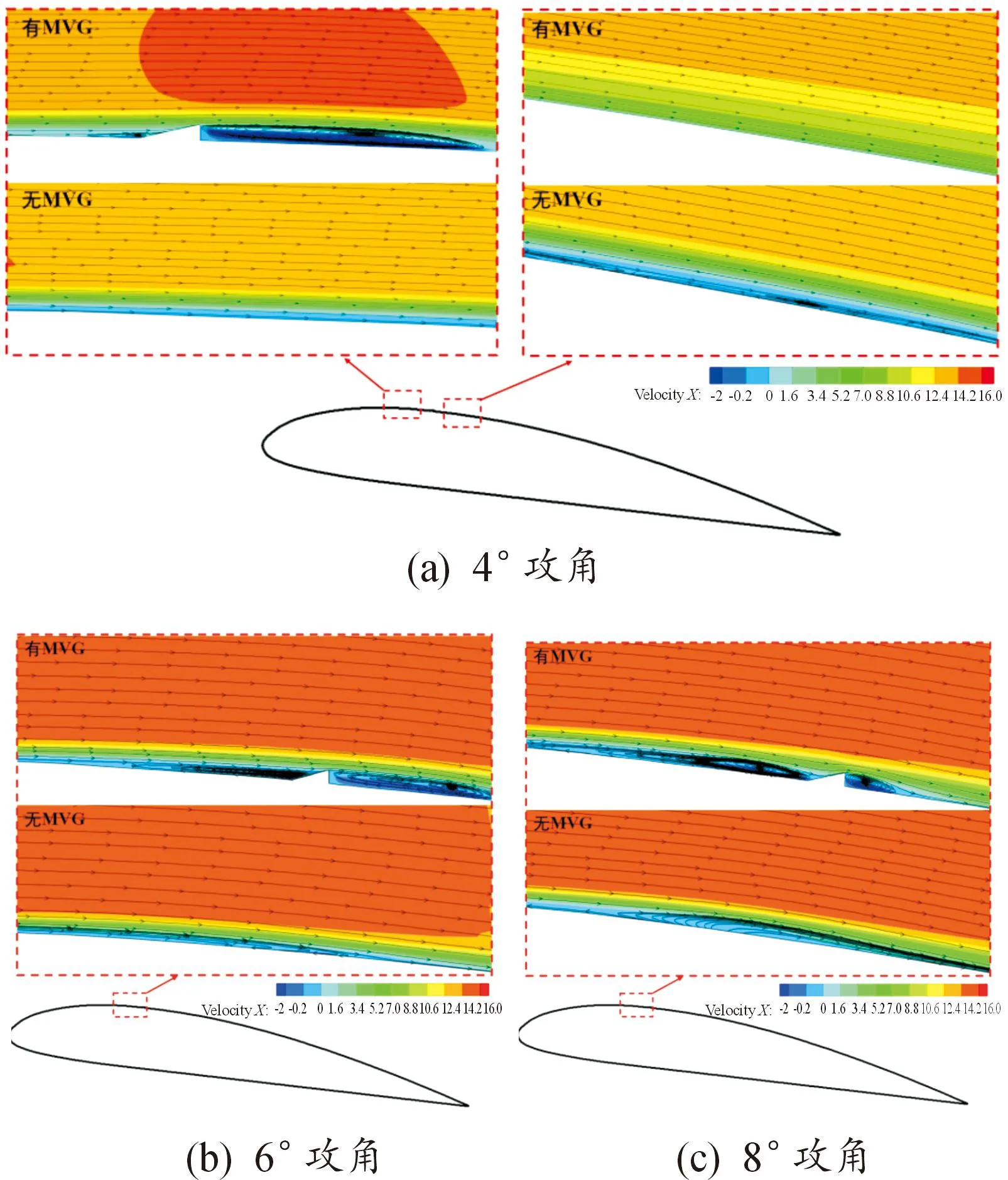
图10 不同攻角条件下MVG附近流线图Fig.10 The streamline neighbouring MVG at different attack angles

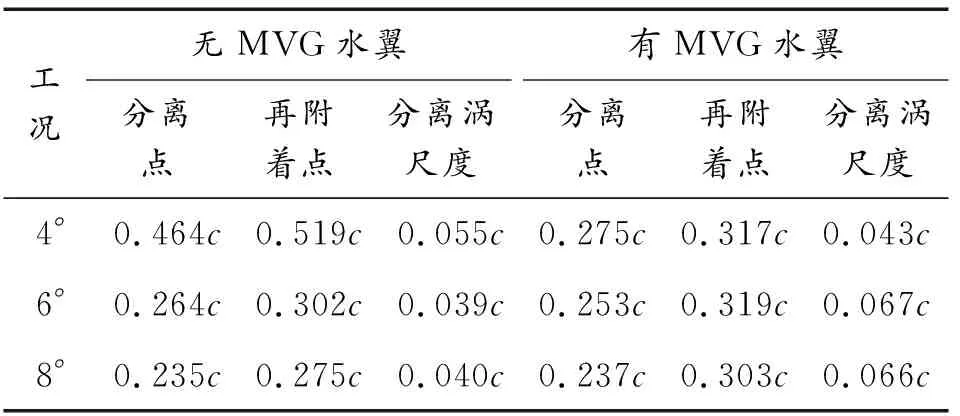
表2 不同攻角条件下有、无MVG水翼流动分离点 和再附着点的位置

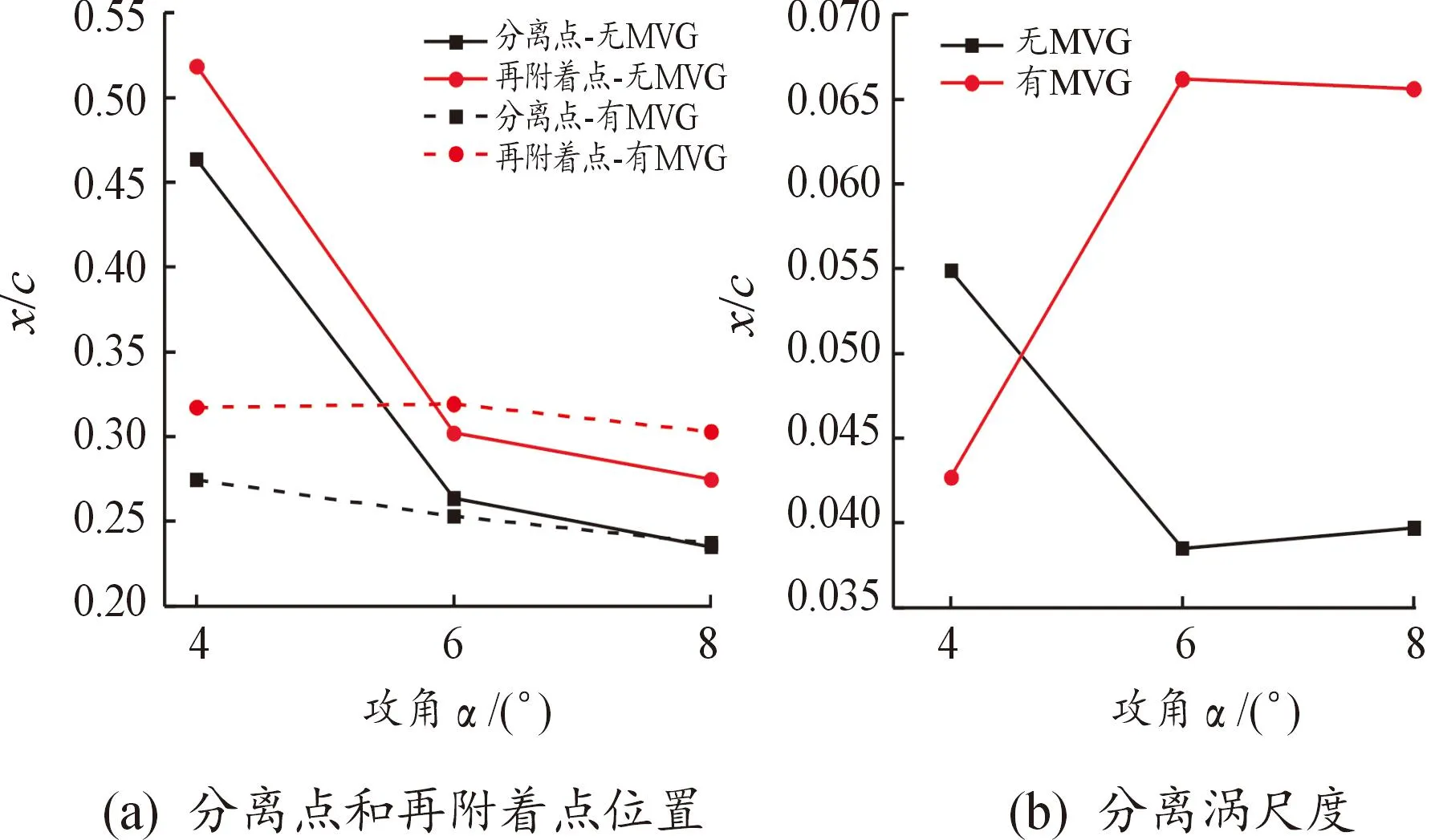
图11 不同攻角条件下流动分离区参数Fig.11 The parameters of flow separation zone at different attack angles

2.2 微型涡流发生器对空化初生特性的影响

通过调整出口压力改变空化数,逐步降低空化数至刚好出现空化,对应空化数即为初生空化数。从表3中可以发现,随着攻角增大,初生空化数增大,并且安装MVG后,各个攻角下的初生空化数均不同程度地下降,对初生空化起到一定的延迟作用,其中,8°攻角时下降幅度较大,降低了7.50%;4°时次之,下降了3.85%;6°时变化不明显,仅下降了0.55%。从图12中的初生空化形态图可以看出,MVG对初生空泡的位置和形态无明显影响,初生空泡均呈片状稳定的贴附在水翼表面,且随着攻角的增大,初生空化的位置逐渐向水翼前缘移动。

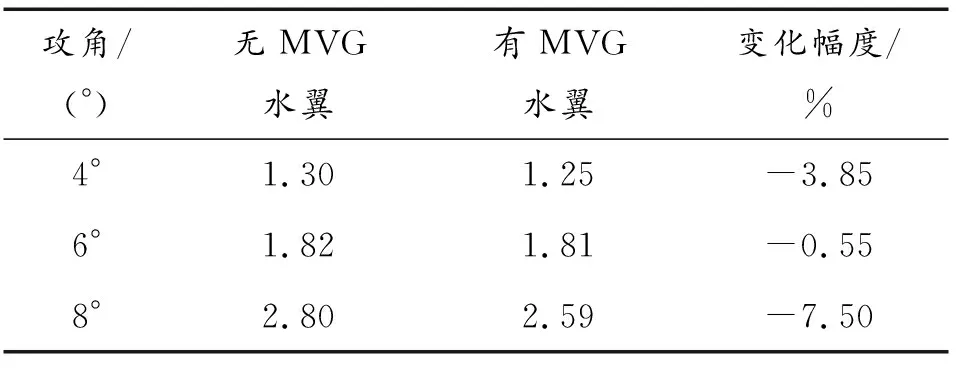
表3 不同攻角下有、无MVG水翼初生空化数对比

图13给出了不同攻角条件下有、无MVG水翼吸力面的压力系数分布。从图13中可以看出,在不同攻角条件下,水翼吸力面压力系数的分布均呈现出先下降后上升的趋势,且随着攻角的增大水翼吸力面的压力整体下降。在安装MVG 后,水翼前缘压力有所增大,最小压力系数也均有所提高,与初生空化数的下降相对应。

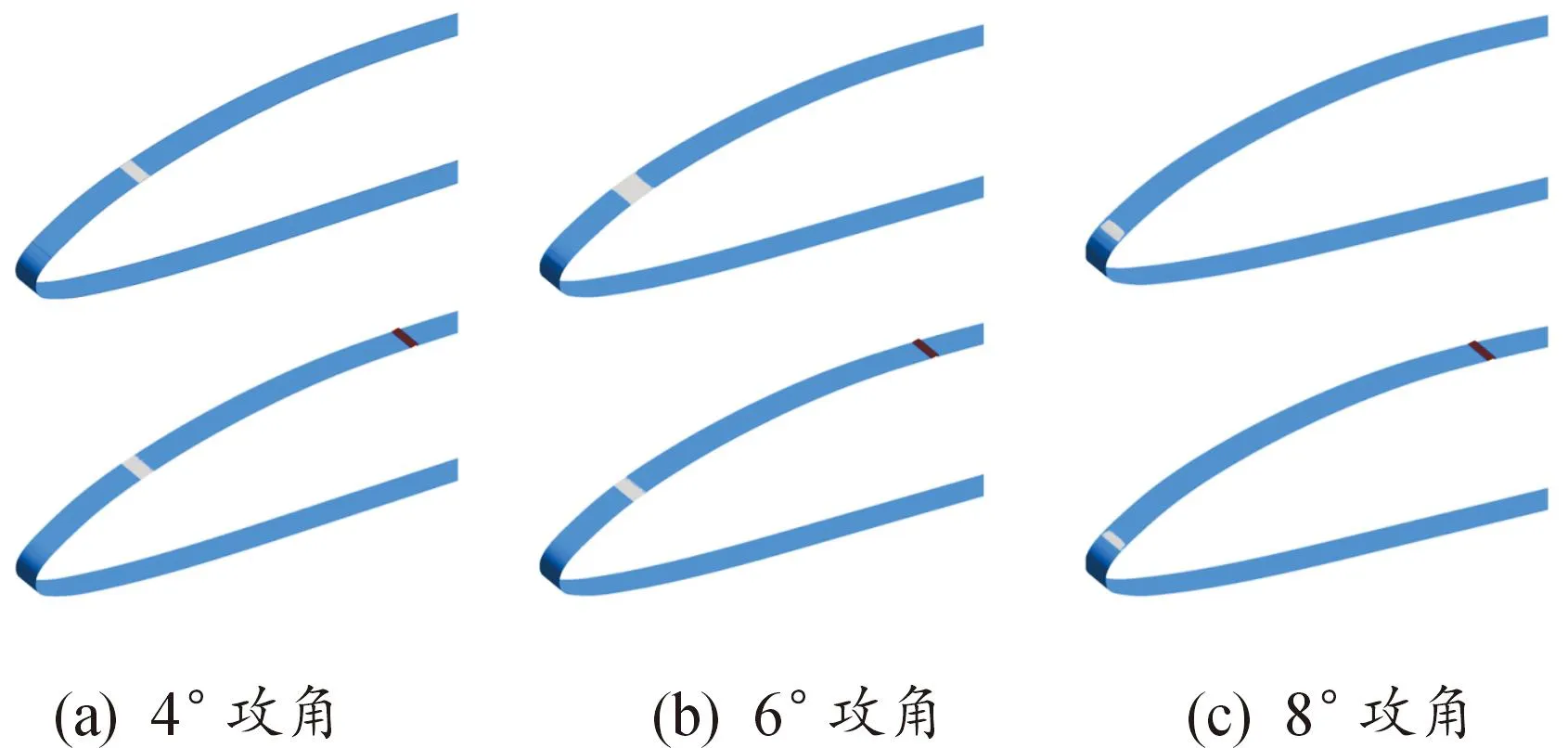
图12 不同攻角条件下初生空化形态

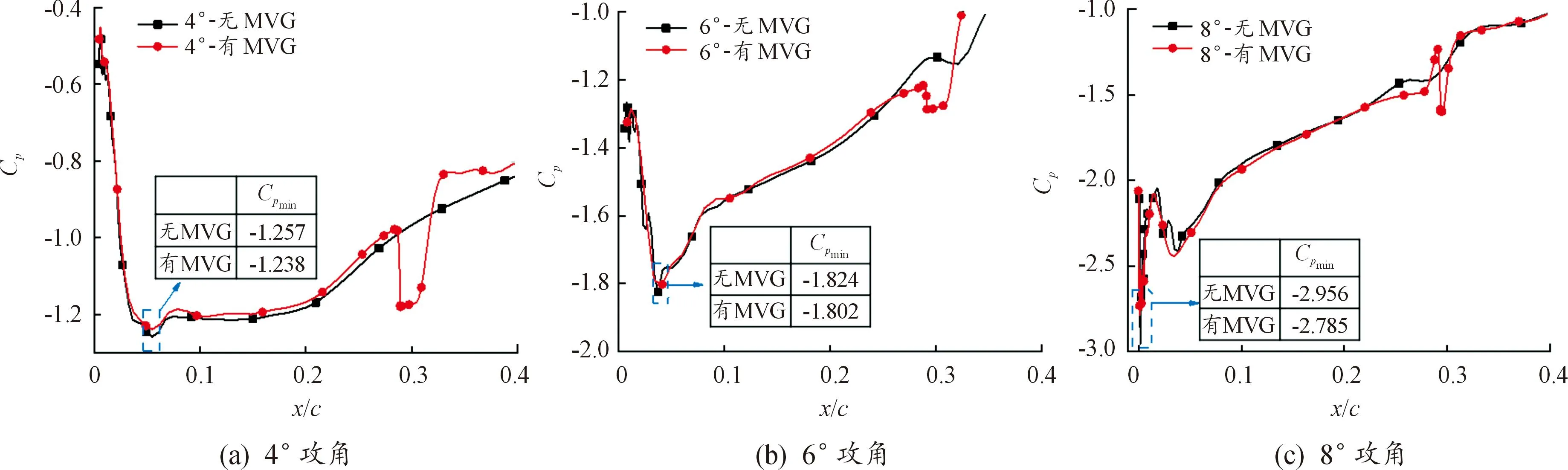
图13 不同攻角条件下有、无MVG水翼吸力面压力分布Fig.13 Pressure coefficient distribution on the suction surface of hydrofoil with MVG and without MVG at different attack angles

表4和表5统计了各攻角下有、无MVG水翼单相流动和初生空化流动下的时均升、阻力系数,并在图14中进行对比。从图14中可以看出,各工况下,水翼的升、阻力系数都随攻角的增大而增大。相较于无MVG水翼,安装MVG后,水翼升力有所下降,阻力有略微增大趋势,但整体上对水翼的水动力性能无产生明显影响。同时,与单相流相比,空化的初生使得水翼的升力有所增加,阻力略微减小。

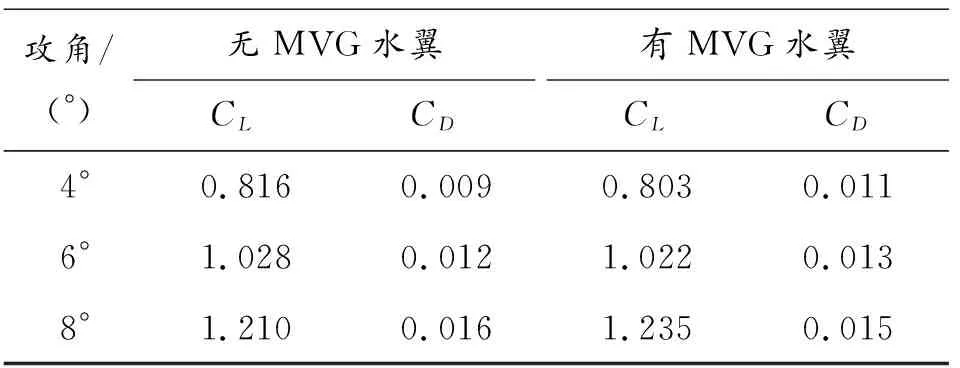
表4 各攻角下有、无MVG水翼单相流动下的 时均升、阻力系数

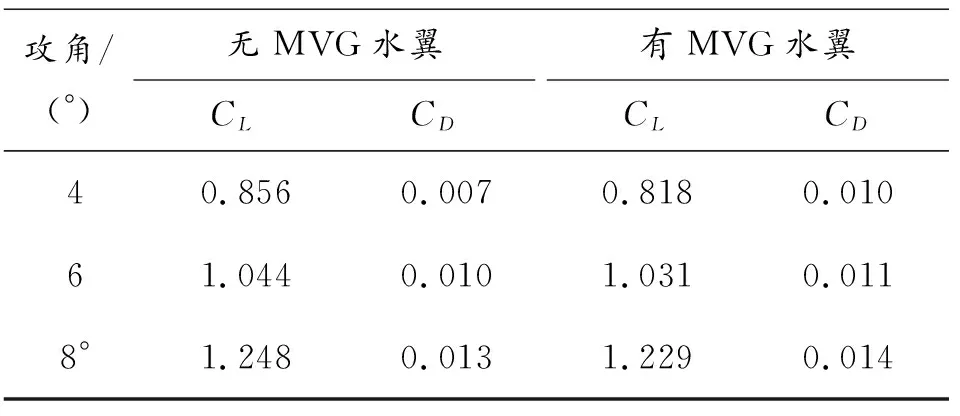
表5 各攻角下有、无MVG水翼初生空化流动下的 时均升、阻力系数

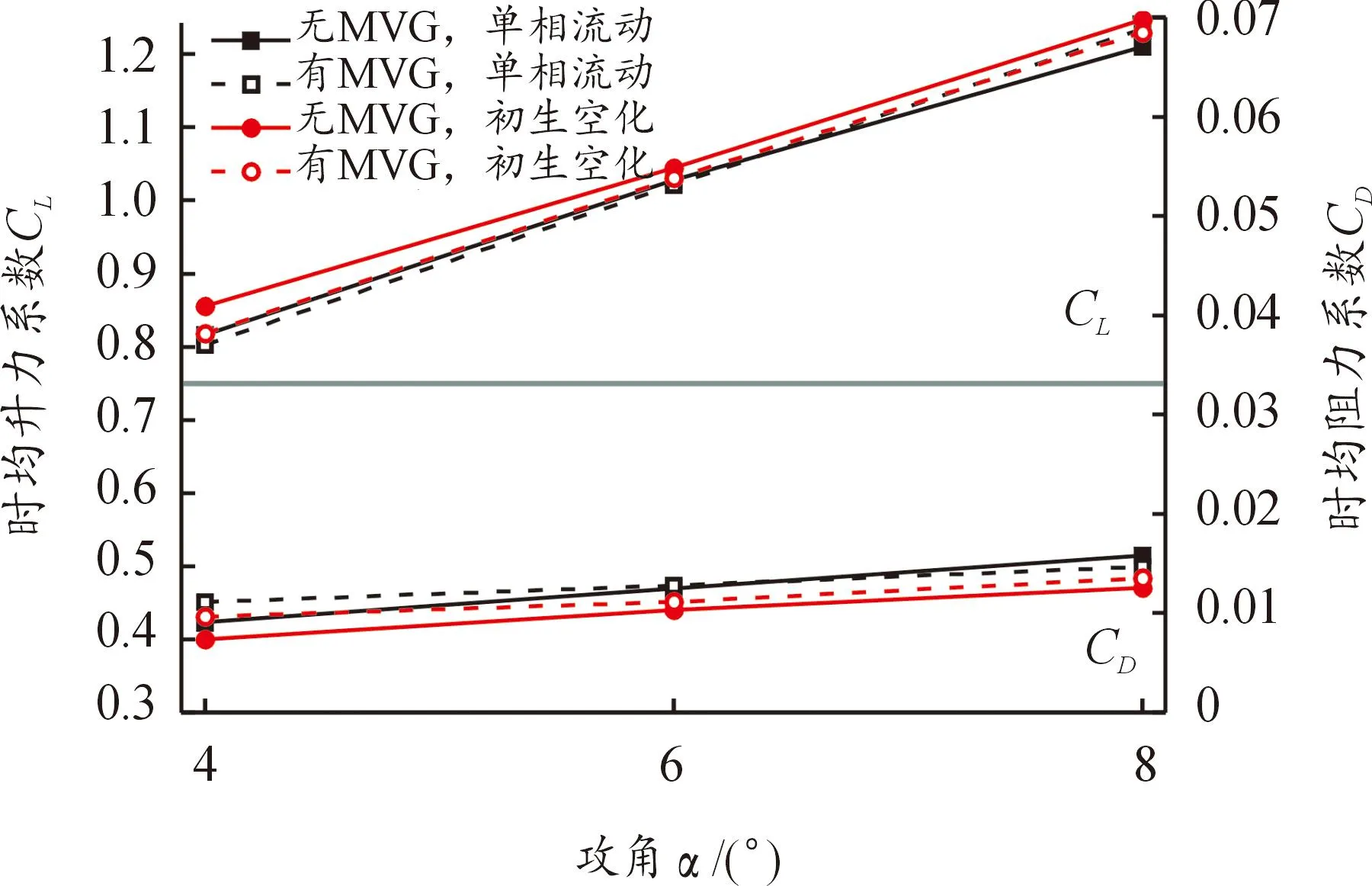
图14 各攻角下有、无MVG水翼时均升、阻力系数比较

3 结论

本文中采用均相流模型,并耦合SSTγ-Reθt湍流模型以及Zwart空化模型对不同攻角下有、无MVG水翼的初生空化流动进行数值计算,研究了MVG对不同攻角水翼流动分离和初生空化特性的影响,得到主要结论如下:

1) MVG可以改变水翼的边界层分离特性。在各攻角条件下,安装MVG均增大了水翼近壁流速,并在MVG的前后端产生了漩涡结构,从而对流动分离区的位置和长度造成影响,同时使得MVG后端边界层一定程度地增厚。随着攻角增大,流动分离涡逐渐向水翼前缘移动。4°攻角时MVG位于分离点之前,基础水翼中部的流动分离被消除,而从MVG前端开始发生分离,分离涡尺度减小,对流动分离起到了一定的抑制作用;6°和8°攻角时MVG位于分离点之后,MVG前端反向射流及后端回流区产生,分离涡尺度增大。

2) MVG可以在一定程度上抑制空化的发生。在各攻角条件下,初生空泡呈片状贴附在水翼表面,MVG的存在使得水翼前缘压力有所增大,最小压力系数提高,从而降低了水翼的初生空化数,对初生空化起到了一定的延迟作用,而对初生空泡的位置和形态以及水翼的时均升阻力不产生明显影响。在4°、6°和8°攻角下,安装MVG后水翼初生空化数分别下降了3.85%、0.55%和7.50%,8°攻角时降幅最大。