基于改进卡尔曼滤波的风电塔筒倾斜监测算法

郑启山,朱少红，陈长红，常海青，晏锡忠，魏晨曦

（1.福建国电风力发电有限公司，福建 福州 350014；2.厦门理工学院，福建 厦门 361024）

0 引言

风电是一种开发成本低，能大规模开发的可再生能源，随着我国经济和科技的快速发展，我国的风电机组数量和规模正在快速增长。

风电场一般都设立在远离人烟的山谷或海上，基本都处于无人值守的状态，因此对风电塔筒设备的运行状况通常利用人工定期巡检来进行维护，这样做会消耗大量的人力和财力[1]，且风电塔筒出现安全问题时不能第一时间通知到管理人员进行维修。风电塔筒属于高耸建筑物，其工作时受到风的推力、自身重力以及叶轮的扭力等复杂多变的负荷影响，导致风电塔筒产生倾斜和较大变形，给邻近建筑物、后期风电工作带来巨大隐患[2]。因此，对塔体的倾斜状态进行实时监测是保障风电机组安全运营的重要措施。

塔筒的角度变化反映出塔筒倾斜和变形的状态，利用倾角传感器可以实现塔筒结构的倾斜以及塔体变形角度的测量。魏锦德等[3]对风机塔筒倾斜的监测方法进行介绍，认为全站仪免棱镜法具有精度高、操作简单的优点，适用于风机塔筒倾斜监测，但该方法的工作效率较低，精度受多重因素影响。三维激光扫描技术也常用于风电塔筒倾斜监测中，史阳军等[4]利用三维激光扫描技术对塔筒的倾斜度、位移量进行计算，但该方法部署环境有限，并不适用于所有风电机组场景。

为了解决风电塔筒的倾斜角不易实时监测，且计算精度低的问题，本文提出基于改进卡尔曼滤波的风电塔筒倾斜监测算法。

主要工作内容如下：

1)对风电塔筒的倾斜角度进行姿态解算，通过数据处理过程中的均值处理零偏，减小零偏对解算的影响；

2)调整姿态解算中卡尔曼滤波方程Rk值，改进卡尔曼滤波方程，提高倾斜角计算精度，减小误差影响。

3)利用Matlab仿真验证改进后的卡尔曼滤波姿态解算精度以及估计值方差收敛程度。

1 姿态解算

本文对风电塔筒倾斜进行监测，通过安装在塔架顶部、塔身处等多个位置的倾角传感器感知风电塔筒倾斜。风电塔筒之间的连接采用法兰盘联接，在塔体内部的不同高度上安装有多个倾角传感器有利于提高塔体位姿及倾斜测量的精度。

姿态解算过程涉及两个坐标系，一个是运载体的坐标系，该坐标系与运载体（风电塔筒）固连，当塔筒发生倾斜、变形等转动时，这个坐标系也跟着转动，假设运载体的坐标系为b系[5]。另外一个是地理坐标系，这个坐标系为n系[6]。姿态解算应用于风电塔筒倾斜监测中，相当于求出当前载体（风电塔筒）坐标系b相对于地理坐标系n的变化。由于n系和b系均为直角坐标系，风电塔筒的倾斜变化可视为两个直角坐标系之间的刚体定点转动，刚体转动可以通过姿态变换矩阵来表示，矩阵中包含了倾角传感器（陀螺仪和加速度计）采集的风电塔筒角运动和线运动等姿态信息[7]。

基于改进卡尔曼滤波的姿态解算实现风电塔筒倾斜监测的主要过程为：利用六轴倾角传感器采集的加速度和角速度数据，通过旋转矢量法更新四元数，从而不断地更新姿态矩阵计算倾斜角度。同时，为了减小倾角传感器中随机误差的影响，利用改进卡尔曼滤波对解算出的倾斜角度进行滤波。

姿态解算过程包括数据处理、初始化和解算3 个部分组成[8]。

数据处理阶段：将陀螺仪和加速度计采集的原始数据导入；然后对陀螺仪的三轴角速度进行零偏校正计算，去掉零偏的不稳定性。

初始化阶段：确定坐标系；设置子样数和采样时间，选择合适的子样数进入姿态解算；初始化加速度计的信息，利用加速度计算初始姿态角，计算过程为：

其中，ax、ay、az表示加速度数据的均值，ψ为初始航向角，γ为初始横滚角，θ为初始俯仰角。

初始化四元数的计算过程为：

为了减少误差对真实值的影响，设置失准角误差值。

解算阶段：依据陀螺输出值，对角速度利用交叉相乘对角速率误差补偿，减掉失准角误差的影响，计算角增量；角增量求模方，如果模方很小，则利用泰勒展开前几项三角函数；如果模方大于阈值，则直接更新四元数旋转矢量的模方为，计算过程如下：

其中，q'0、q'1、q'2、q'3是利用旋转矢量计算后的四元数，与原四元数计算更新四元数q。对更新后的四元数归一化：

依据坐标系的关系，利用四元数转换姿态转移矩阵，计算过程如下：

计算姿态角过程如下：

2 基于改进卡尔曼滤波的姿态解算

2.1 卡尔曼滤波

卡尔曼滤波是一种高效率的递归滤波器，能够在不同时间下的各测量值中估计系统的状态[9]。卡尔曼滤波不同于依靠历史值估计结果的滤波器，它能够结合上一时间状态的结果和当前时间状态的值估计出结果。

卡尔曼滤波依靠预测和更新这两个功能实现最优估计，如图1所示。

图1 卡尔曼滤波流程

在预测阶段，利用上一时刻的状态估计，对当前时刻的状态进行预测，通过状态预测方程和协方差矩阵预测方程来实现；在更新阶段，利用当前时刻状态的观测值与真实值之间的差，优化当前时刻的状态预测值，并计算卡尔曼增益值，更新一个更精确的估计值，通过增益方程、状态更新方程和协方差更新方程来实现测量更新校正的功能[10]。

卡尔曼滤波通过下述5个方程实现预测和更新状态的过程。

1）系统状态预测方程

2）协方差矩阵

3）增益方程

4）状态更新方程

5）协方差更新方程

2.2 改进卡尔曼滤波

由于传统卡尔曼滤波在长时间工作状态下存在滤波发散的问题，而对于风电塔筒的倾斜监测是一个长期且实时的过程，长期监测需要卡尔曼滤波具备自适应功能，因此，需要对卡尔曼滤波进行改进，不断地调整其中误差值，并有效滤除[11]。

卡尔曼滤波中的有些参数是无法获得的，例如Qk和Rk，都是根据经验、实验或数据手册得到的。从传统的卡尔曼滤波方程中可以看出，Rk越大，增益Kk越小，而Rk越小，Kk越大，Kk值影响着当前状态的预测值。

本文提出一种自适应调整Rk的方法，不需要精确的初值，且在滤波过程中自适应地变化其值的大小，从而使滤波结果具有较高的精度。

对Rk进行优化，公式如下：

其中，r是一个自适应调节的参数，调节Rk的权重。Rk通过式（32），在利用实测数据的同时对模型和噪声统计特性进行估计和修正，进而修改滤波设计和滤波误差，自适应地更新Rk大小，不断优化增益Kk值。

2.3 算法流程

基于改进卡尔曼滤波的姿态解算的算法流程图如图2所示。

图2 基于改进卡尔曼滤波的姿态解算算法流程

3 实验结果与分析

3.1 实验平台与参数设置

本文通过Matlab 2019a仿真软件对比改进卡尔曼滤波前后的姿态角数据，从中分析风电塔筒中倾斜角计算精度；再对比传统卡尔曼滤波和改进卡尔曼滤波的误差估计数据，分析验证改进卡尔曼滤波在估计误差精度方面优于传统的卡尔曼滤波；最后仿真分析姿态角误差值的方差收敛状态，验证改进后的卡尔曼滤波对误差的收敛作用。

改进后卡尔曼滤波算法在初始化阶段需要设置一些仿真参数的初值[13]，如表1所示。

表1 初始化参数设置

3.2 倾斜角计算精度分析

经过改进卡尔曼滤波后的角度与实际值进行对比，结果如图3所示，其中（a）、（b）、（c）分别为θ、ψ、γ角的实际值与改进后的卡尔曼滤波解算值的对比。

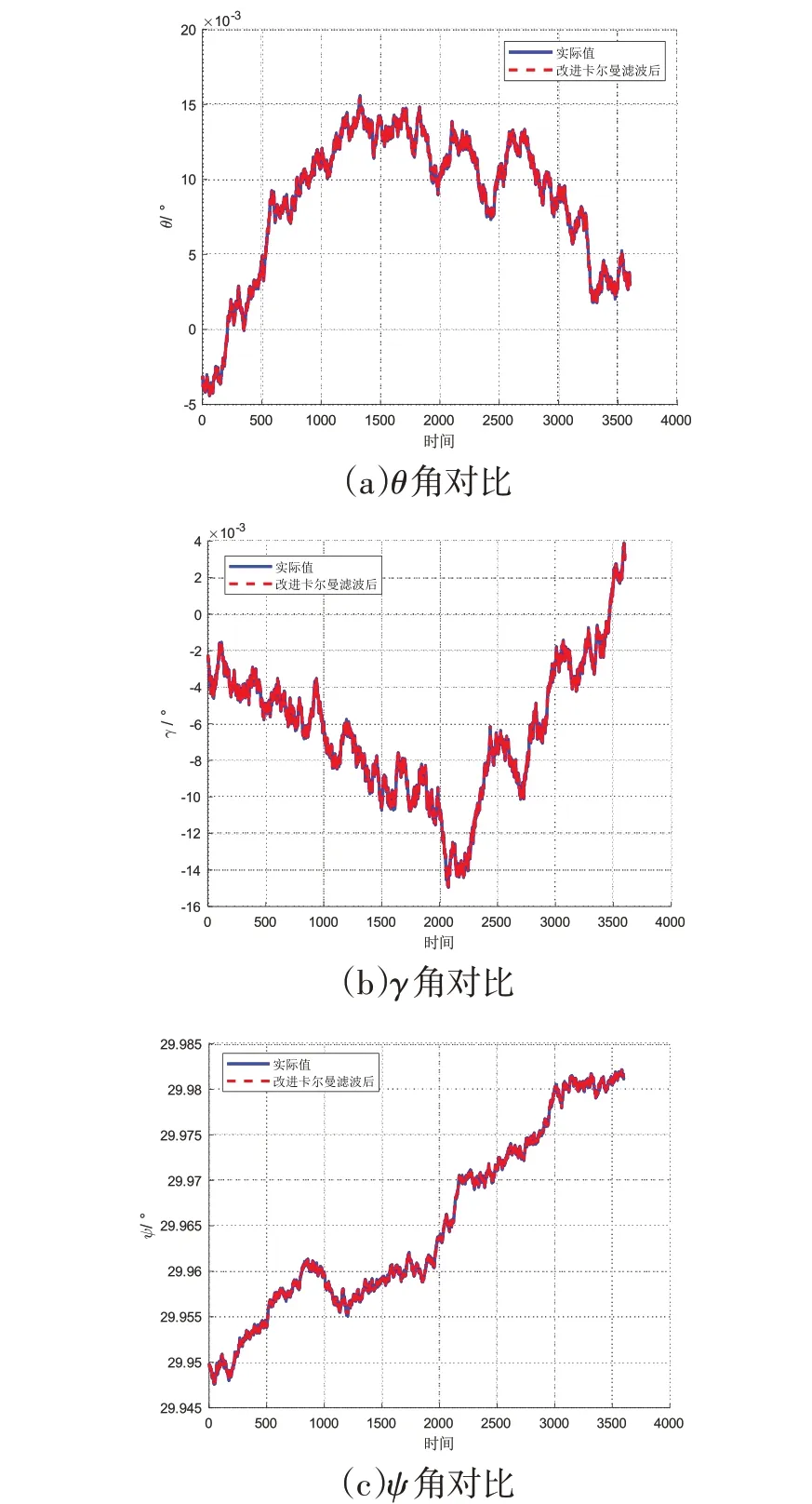
图3 姿态解算与改进卡尔曼滤波后的解算值对比

从图3 可以看出，实际值与改进卡尔曼滤波后的解算值一致，解算无偏差，说明本文提出的改进卡尔曼滤波算法的解算精度高，对于风电塔筒的倾斜监测准确率高。

3.3 状态真值与估计效果对比

对比传统卡尔曼滤波估计值、改进卡尔曼滤波估计值与状态真值（失准角），结果如图4所示。

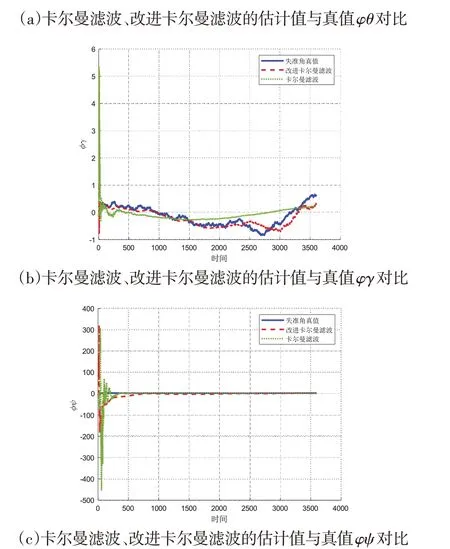
图4 姿态解算与改进卡尔曼滤波后的解算值对比

从图4可以看出，改进卡尔曼滤波的估计值φθ、φγ和φψ相较于传统卡尔曼滤波的估计值总体上更加接近失准角真值，说明改进卡尔曼滤波算法能够更为准确地估计出姿态误差值（失准角），减小误差对风电塔筒倾斜角计算的影响。

3.4 姿态误差值的方差收敛分析

改进卡尔曼滤波所计算的姿态误差值方差结果如图5所示。

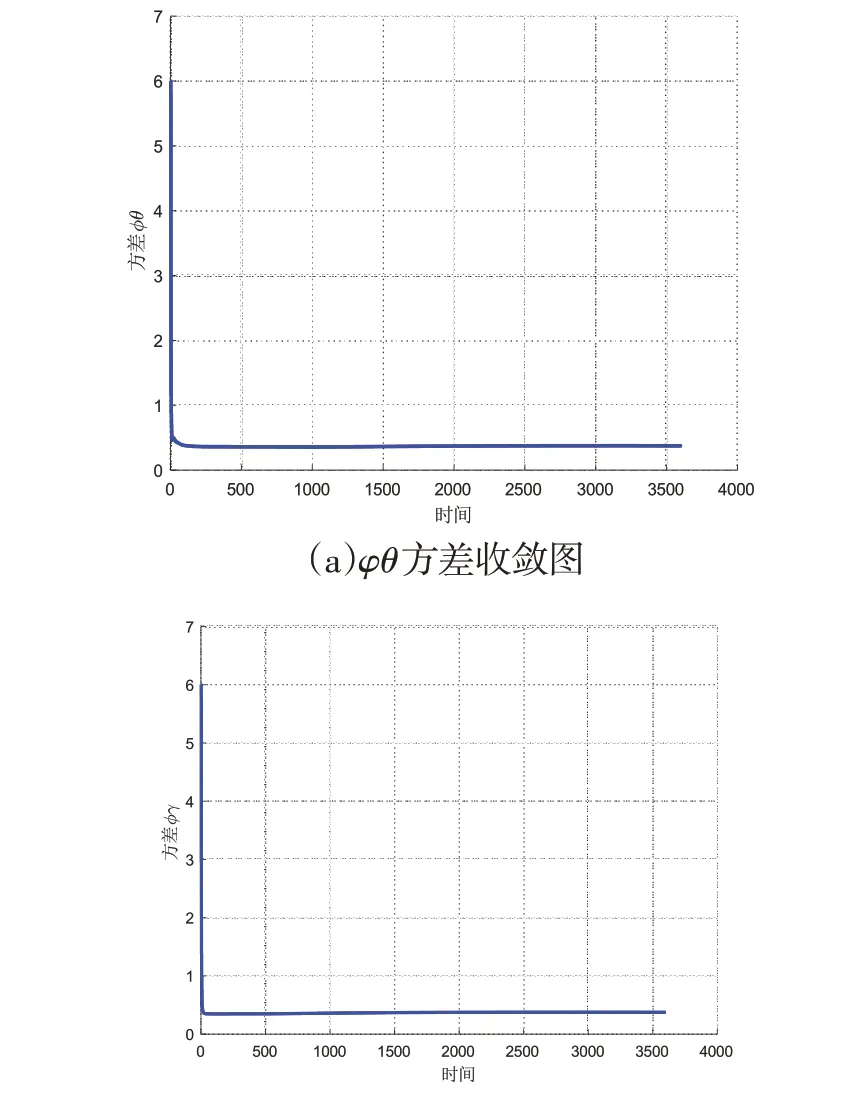
图5 各失准角的方差收敛状态

从图5中看出，φθ、φγ和φψ都随着时间的增加方差逐渐收敛，且趋势稳定。φθ的方差从6一直在收敛，最终在3 600s时收敛到0.375；φγ的方差最终在3 600s时收敛到0.375；φψ的方差也越来越低，最终从600收敛到27.75。姿态误差值的方差越来越低，说明改进卡尔曼滤波的估计误差值越稳定。

4 结论

本文对于风电塔筒的倾斜角不易实时监测，且计算精度低的问题，提出基于改进卡尔曼滤波的风电塔筒倾斜监测算法。主要通过姿态解算的数据处理环节，剔除零偏影响，以及自适应调整卡尔曼滤波方程中的Rk值，优化滤波增益来改进卡尔曼滤波算法，实现风电塔筒无人智能监测，得出以下结论。

1）改进后的卡尔曼滤波在解算倾斜角时的精度高；

2）改进后的卡尔曼滤波估计值相较于传统卡尔曼滤波更加接近真实误差值，滤除误差效果优于传统卡尔曼滤波；

3）改进后的卡尔曼滤波姿态误差方差越来越低，估计出的误差值稳定收敛。