蒸汽管道动态水力热力特性研究

2024-01-04肖木森郭磊宏齐智猛章雨然

煤气与热力 2023年12期

肖木森, 张冲, 郭磊宏, 齐智猛, 范巍, 章雨然

(1.天津市津安热电有限公司,天津 300000;2.天津大学环境科学与工程学院,天津 300350)

1 概述

蒸汽热网是集中供热系统中连接热源和用户的纽带,关系到生产运营安全和系统能源利用效率。蒸汽作为载热介质,可同时满足不同压力和温度要求的多种用户的用热需求,适用性较广。蒸汽密度小,因此蒸汽系统适用于高层建筑的供暖,不容易使底部设备超压。蒸汽热惰性小,供汽时热得快,停汽时冷得也快,因此在工业生产的各个工艺环节中,蒸汽系统也得到了广泛的应用[1-2]。

相比于热水供热系统,蒸汽供热系统内蒸汽流动状态复杂多变,且出现故障危害大,了解蒸汽在管道中流动的水力状态和热力状态不仅能够促进蒸汽管网调控向智能化、精细化转型,也能够提高整个供热系统的安全可靠性。因此有必要对蒸汽热网建立准确且高效的水力热力耦合数学模型,并能在负荷频繁波动和室外温度周期性波动运行工况下计算出供热管网中各管段、各末端蒸汽的水力状态和热力状态[3-5]。

国内外学者针对蒸汽管网的水力模型和热力模型开展了一系列研究,史琳等人[6]考虑蒸汽为可压缩理想气体,建立了蒸汽管网的水力热力耦合模型,可以计算流量分配以及温度、压力分布,并将该模型应用到大型蒸汽管网中。李世武[7]提出了蒸汽管网的模拟计算方法,该方法基于节点模拟法,以节点方程为基础,提出了蒸汽管网计算的节点残量修正计算方法。Kiuchi[8]采用全隐式有限差分法计算管网中的非稳态气体流动,并基于牛顿-拉夫逊法求解管道有限差分方程。Bermudez等人[9]介绍了管道内实际气体非等温、非绝热可压缩流动数学模型数值求解的有限体积格式,采用了Van Leer的Q-Scheme数值格式对数学模型中的通量进行迎风离散,与标准欧拉方程不同,该模型考虑了壁面摩擦、变高度以及管道与环境之间的传热。Marconcini等人[10]利用连续性方程、动量方程和能量守恒方程,编写了非绝热蒸汽管网中过热蒸汽流动状态参数的计算机程序VAPSTAT1,它通过计算流体在给定节点的流量、压力和温度来模拟蒸汽管网。

虽然在蒸汽管道建模及仿真方面已有较多研究,但大部分研究对蒸汽在管道流动过程中的状态参数变化考虑不足,或将其忽略,或认为蒸汽是理想气体并进行简化计算,但蒸汽的状态参数变化直接影响到蒸汽管道水力热力模型计算的准确性。因此,本文综合考虑蒸汽作为非理想气体的状态方程和焓方程,以质量守恒、动量守恒和能量守恒定律为基础,建立蒸汽管道水力热力耦合特性的非稳态模型,并模拟分析在环境温度周期性变化、管道入口压力变化、管道入口温度变化这3种常见的非稳态工况下,管道内蒸汽参数的变化情况,得到其变化的一般性规律。

2 蒸汽管网动态水力热力特性研究方法

2.1 蒸汽状态参数方程

蒸汽为可压缩流体,在管道内流动过程中,蒸汽压力、温度的不断变化会导致其比体积、比焓的变化,因此蒸汽比体积、比焓的状态方程与蒸汽在管道中流动的控制方程相互联系。本文采用蒸汽的状态方程如下[11]:

(1)

(2)

式中v--蒸汽比体积,m3/kg

p--蒸汽压力,Pa

Rm--蒸汽气体常数,J/(kg·K)

T--蒸汽温度,K

Cp--蒸汽的无量纲压力,为蒸汽压力与参考压力的比值,参考压力取1 MPa

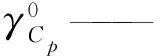
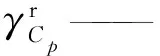
h--蒸汽比焓,J/kg

CT--蒸汽的无量纲温度,为蒸汽温度与参考温度的比值,参考温度取540 K

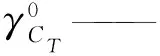
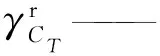
理想及剩余部分的无量纲压力、温度关联式的计算方法依次如下:

(3)

(4)

(5)

(6)

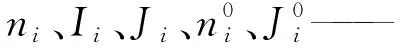
计算系数的取值见表1,式(5)中计算系数的取值见表2。

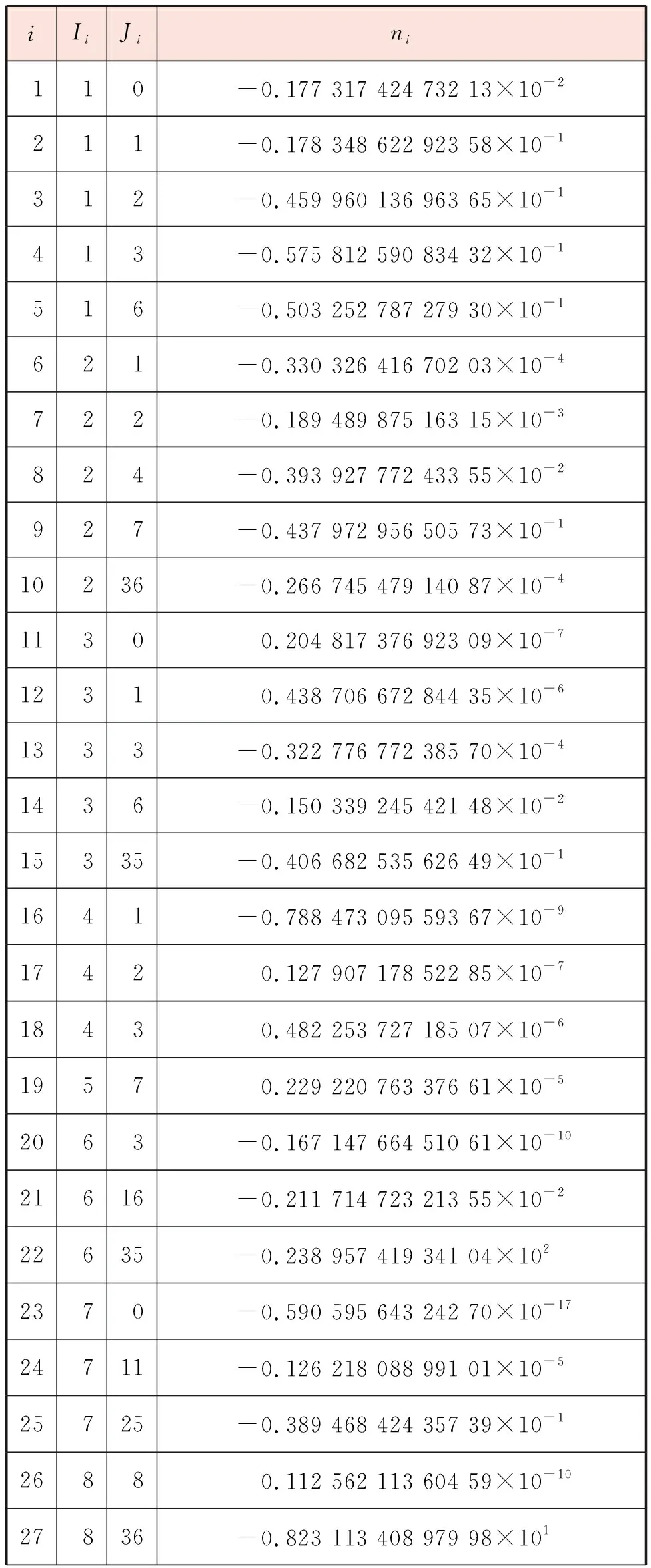
表1 式(4)与式(6)中计算系数的取值[11]

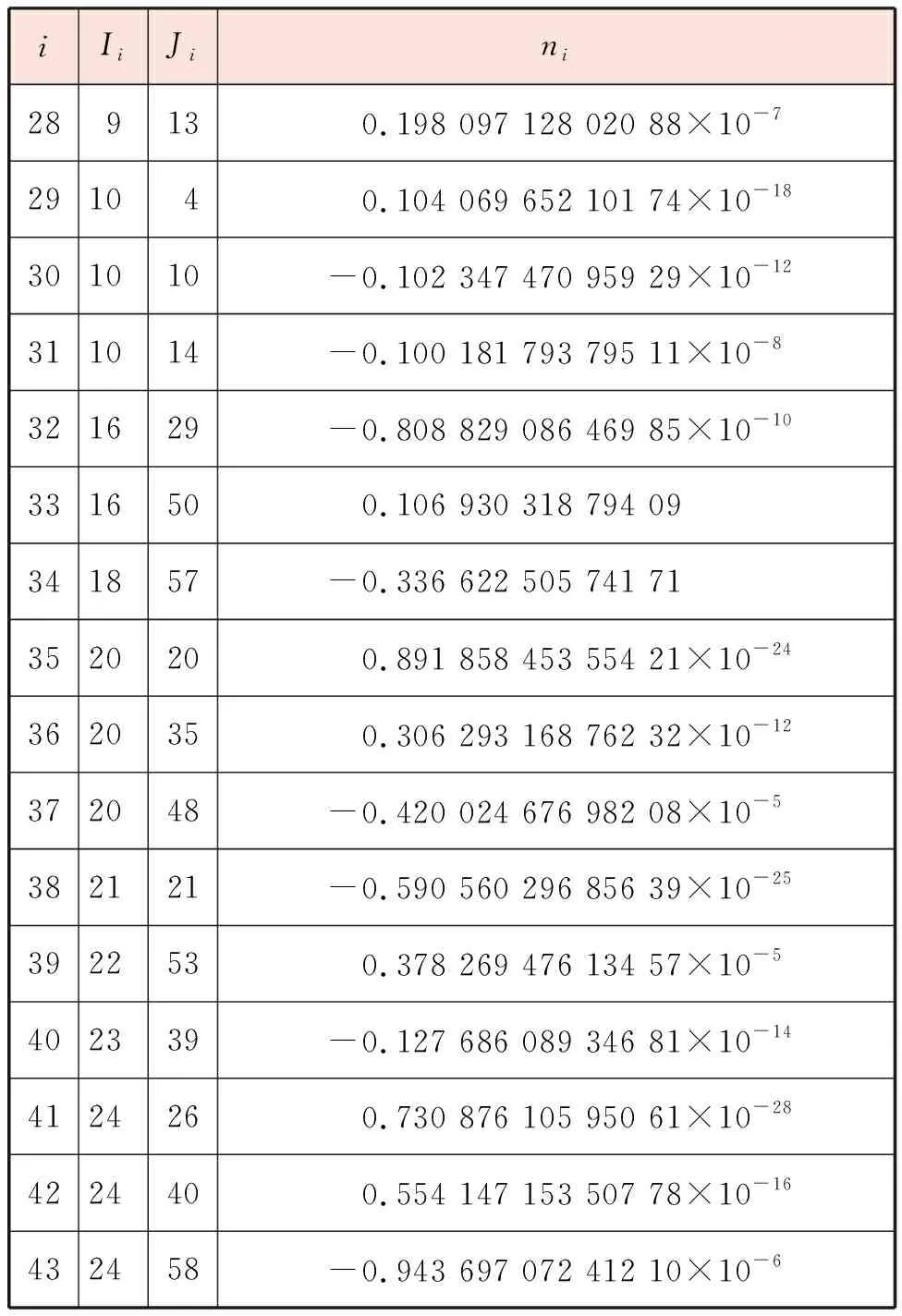
续表

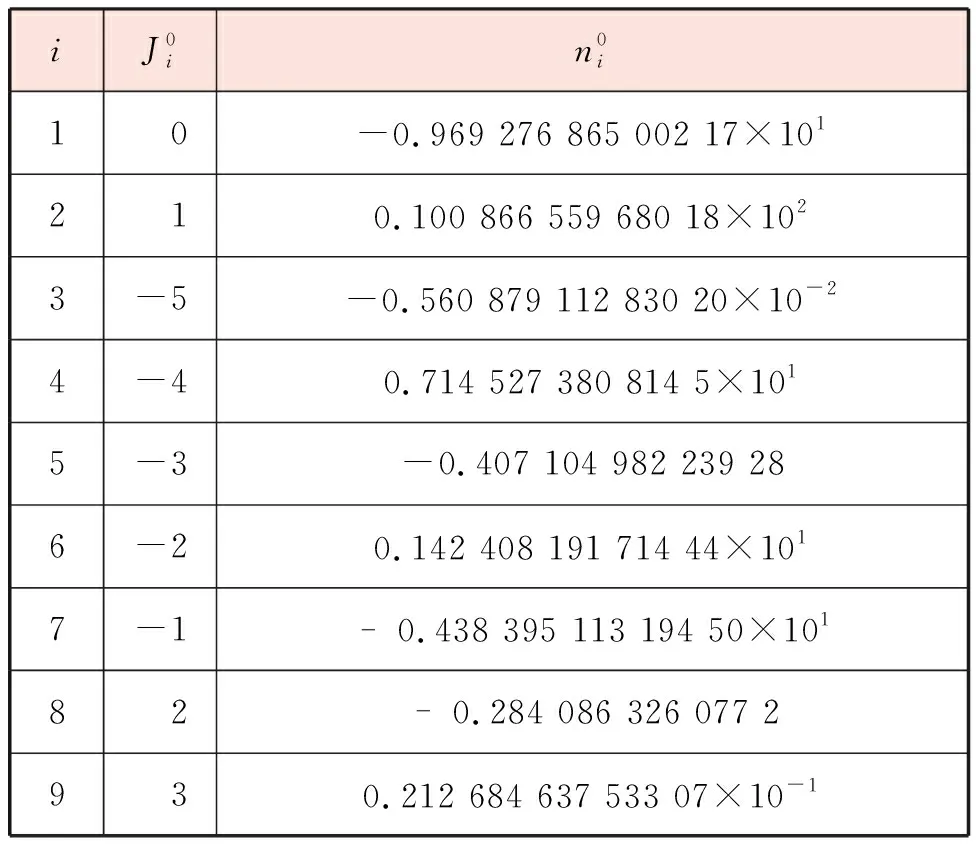
表2 式(5)中计算系数的取值[11]

蒸汽动力黏度随蒸汽温度和压力变化而变化,本文采用的蒸汽动力黏度计算公式如下[12],此处蒸汽的无量纲温度的参考温度取值与前文不同,取647.096 K。

Cμ=Cμ0Cμ1Cμ2

(7)

(8)

(9)

式中Cμ--蒸汽无量纲动力黏度,为蒸汽动力黏度与参考动力黏度的比值,参考动力黏度取1.00×10-6Pa·s

Cμ0--蒸汽在稀释气体极限下的无量纲动力黏度

Cμ1--有限的密度对蒸汽无量纲动力黏度的影响

Cμ2--蒸汽无量纲动力黏度的临界增强,临界增强仅在临界点附近的密度和温度非常小的区域显著,本文的蒸汽状态区域与临界点距离较远,在此不考虑,取1

Hi、Hij--计算系数

Cρ--蒸汽无量纲密度,为蒸汽密度与参考密度的比值,参考密度取322.0 kg/m3

式(8)中计算系数Hi的取值见表3,式(9)中计算系数Hij的取值见表4。

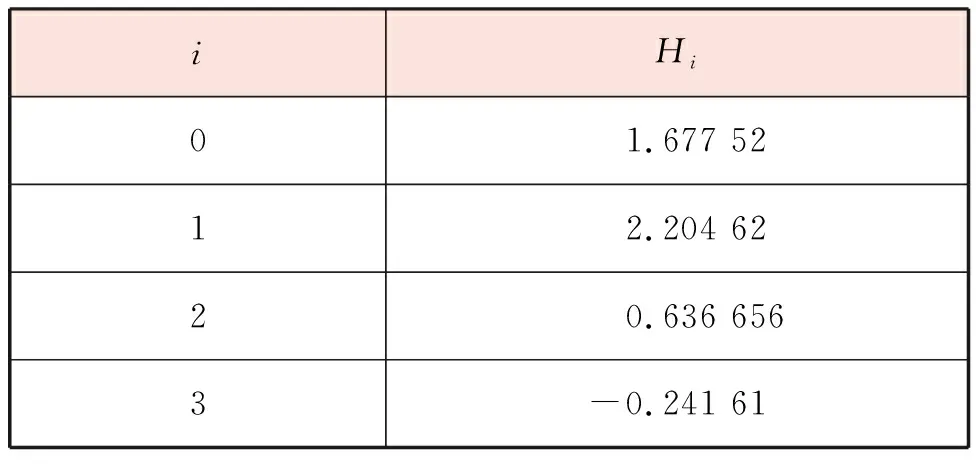
表3 式(8)中计算系数Hi的取值[12]

表4 式(9)中计算系数Hij的取值[12]

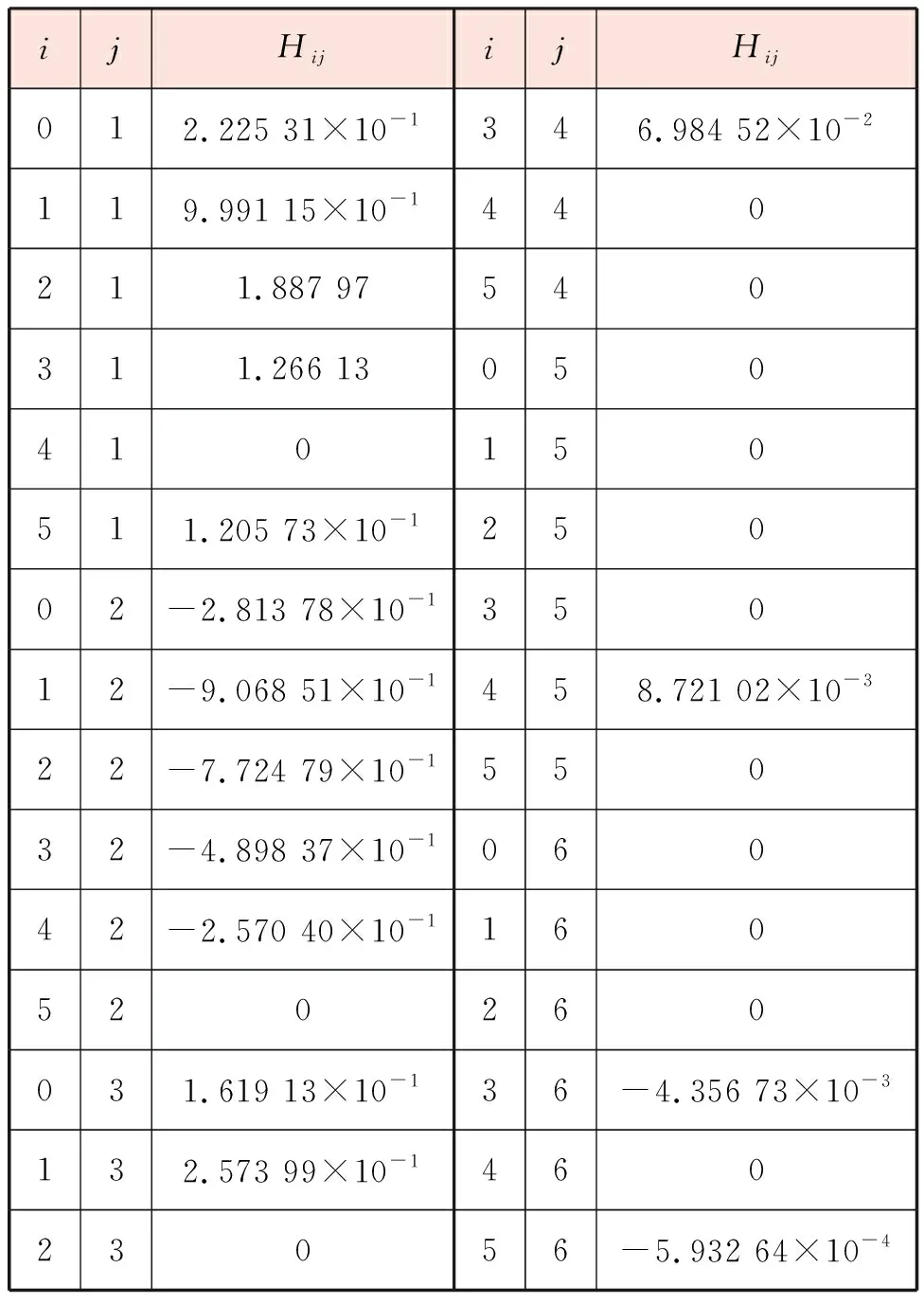
续表

2.2 蒸汽管道动态模型

蒸汽在管道中的实际流动过程十分复杂,为了便于模型的建立与求解,进行了以下两项假设:在实际管网中,管道长度远大于管道外直径,故假设蒸汽管道是一维的,即蒸汽参数沿管道直径方向保持恒定;蒸汽通过管壁和保温层向环境传热,传热系数沿管道变化不大,故将传热系数视为常数。对蒸汽管道进行控制体划分及分析,蒸汽管道外存在保温层,内部包含蒸汽主流,可压缩流体(即蒸汽)通过垂直于流向的截面积为A的管道,其受到重力、管壁摩擦、流体压力等作用,并时刻与外界环境进行热交换,状态参数不断发生变化。

蒸汽在管道中流动满足质量守恒,其连续性方程如下[13]:

(10)

式中ρ--蒸汽密度,kg/m3

t--时间,s

u--蒸汽速度,m/s

x--某个节点距坐标原点的距离,m

蒸汽在管道中为一维流动,且速度较大,忽略黏性切应力引起的动量交换,则蒸汽在管道中流动的动量守恒方程如下:

(11)

式中f--蒸汽在管道中流动的沿程阻力系数

dpi--蒸汽管道的内直径,m

g--重力加速度,m/s2,取9.801 1 m/s2

θ--蒸汽管道与水平方向的夹角

沿程阻力系数f是雷诺数Re和管道内表面粗糙度的函数,其关系式是通过实验或者半理论分析得到的。本文采用阿里特苏里公式,其计算方便,且适用性较广。阿里特苏里公式如下所示:

(12)

式中Δ--管道内表面粗糙度,m

Re--雷诺数

蒸汽在管道中不断与环境进行热交换,对于可压缩流体,蒸汽温度的变化会导致蒸汽密度的变化,从而影响流场的分布,故需要计算蒸汽沿管道的温度分布。忽略导热产生的热量交换,则蒸汽在管道中流动的能量守恒方程如下:

(13)

式中k--蒸汽与环境的传热系数,W/(m2·K)

Ta--环境温度,K

对于架空管道,蒸汽在管道中流动的传热由5部分组成,包括蒸汽与管壁的对流传热、管壁的导热、保温层的导热、保温层外壁与空气的对流传热以及保温层外壁与空气的辐射传热。在以管道公称直径计算传热面积的条件下,该过程的传热系数计算式如下:

(14)

式中dp--管道公称直径,m

hm--蒸汽与管壁的表面传热系数,W/(m2·K)

dpo--管道的外直径,m

λp--管道热导率,W/(m·K)

dio--保温层的外直径,m

λi--保温层热导率,W/(m·K)

ha--保温层外壁与空气的表面传热系数,W/(m2·K)

hr--保温层外壁的辐射传热系数,W/(m2·K)

2.3 动态模型的离散与求解

2.3.1动态模型的离散

首先对动态模型进行离散。本文在上述模型计算中采用交错网格技术,选取有限容积法中的控制容积积分法,对上述方程进行离散。考虑到蒸汽在管道中流速很快,通过对流传递的热量比通过导热传递的热量大很多,采用一阶迎风格式可以满足计算精度。离散所采用的交错网格见图1。

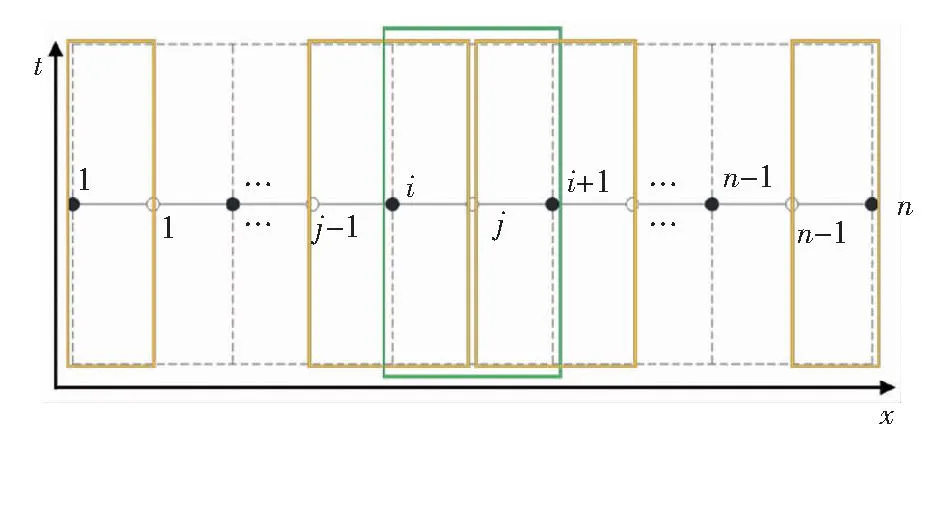
图1 交错网格分布

主控制体以物性节点(空心圆点)为中心,速度节点(实心黑点)位于主控制体的边界。相邻两个速度节点间的距离为一个控制体长度Δx。主控制体内部,储存了该控制体的蒸汽压力、蒸汽密度、蒸汽温度(蒸汽比焓)等信息,而主控制体的边界储存速度,同一个主控制体的左右两个边界速度不一定相同。

从左边起,第1个节点为i=1,储存入口蒸汽速度,第2个节点为j=1,储存入口蒸汽压力与入口蒸汽温度。第3个节点为i=2,第4个节点为j=2,以此类推,倒数第2个节点为j=n-1,最后1个节点为i=n。

采用分段线性假设计算密度及动量,并利用一阶迎风格式对上述控制方程进行离散,过程如下。

① 动量方程

对t时刻节点i所在的控制体进行积分,方程如下,式中量的符号上标表示时间,下标表示节点。方程系数除外,其上标表示节点。

(15)

式中 ΔV--控制体体积,m3

Δt--离散时间单位,s

Δx--离散空间单位,m

速度、密度的计算采用一阶迎风格式,按下式计算:

(16)

对控制体交界处的密度采用分段线性假设,能够得到以下关系式:

(17)

(18)

将式(18)整理成下式形式:

(19)

方程系数的计算式为:

(20)

(21)

(22)

(23)

式(19)～(23)构成离散的动量方程。

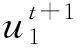
(24)

(25)

当i=3,…,n-1时,方程系数按式(20)～(23)计算。

当i=n时,动量方程出口的边界条件采用了局部单向化假设,即计算结果依赖于n-1节点,不依赖于外界环境,控制体长度变为正常的一半。此时,离散的动量方程的系数有两项产生了改变,式(20)变为式(26),式(23)变为式(27):

(26)

(27)

② 连续性方程

对节点j所在的控制体进行积分,方程如下:

(28)

式(28)可化简为:

(29)

将式(17)代入式(29)可得:

(30)

此处引入压力与速度的修正方程。压力修正方程如下:

p=p*+p′

(31)

式中p*--压力计算项,Pa

p′--压力修正项,Pa

速度修正方程如下:

u=u*+u′

(32)

式中u*--速度计算项,m/s

u′--速度修正项,m/s

修正后的速度u应满足式(30),则将式(32)代入式(30)可得:

(33)

根据式(19)计算出的速度计算项u*和压力计算项p*满足动量方程,因此以下关系式成立:

(34)

(35)

速度修正项u′及压力修正项p′满足式(19),所以将式(32)代入式(19),可以得到以下关系式:

(36)

(37)

由此,联立式(34)与式(36),式(35)与式(37),可以得到以下关系式:

(38)

(39)

忽略相邻节点的影响,规定以下关系式成立:

(40)

将式(39)、(40)代入式(38),得到速度修正项u′与压力修正项p′的关系:

(41)

将式(41)代入式(33)可得:

(42)

整理得到:

(43)

为了简化方程的形式,再次将式(17)逆向代入式(43),可以得到:

(44)

将式(44)整理为下式形式:

(45)

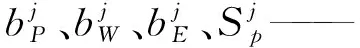
方程系数的计算式为:

(46)

(47)

(48)

(49)

式(44)～(48)为离散的连续性方程。

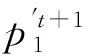
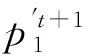
(50)

当j=3,…,n-2时,离散的连续性方程的系数按式(46)～(48)计算。

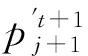
(51)

(52)

③ 能量方程

对节点j所在的控制体进行积分,方程如下:

(53)

式(54)可化简为:

(54)

比焓的计算采用一阶迎风格式,按下式计算:

(55)

将式(55)代入式(54),可以得到:

(56)

化简并整理得到:

(57)

将式(57)整理成下式形式:

(58)

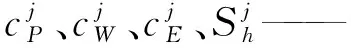
方程系数的计算式为:

(59)

(60)

(61)

(62)

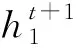
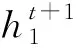
(63)

(64)

当j=3,…,n-2时,方程系数按式(59)～(62)计算。

当j=n-1时,能量方程出口的边界条件采用了局部单向化假设,即计算结果依赖于n-1节点,不依赖于外界环境,此时,离散的能量方程系数有一项产生了改变:

(65)

至此,完成了所有方程的离散。

2.3.2动态模型的求解

计算上述离散方程时,认为管道入口蒸汽状态(蒸汽温度、蒸汽速度、蒸汽压力)已知,且已知管道长度、公称直径(管道外直径、壁厚)、保温层厚度、管壁粗糙度、环境温度、蒸汽与环境的传热系数、管道坡度,给定离散时间单位和离散空间单位,可以通过以下步骤对上述模型进行求解,得到某一时刻管道出口的蒸汽温度、蒸汽压力及蒸汽速度。

① 将计算的初始时刻称为t时刻。将t时刻各个节点的ρ、u、h设置为与入口边界相同。以下开始求解t+1时刻各个节点的p、u、T、ρ、h、μ,为简化符号,省略以下步骤②～⑦中符号的上标t+1。

② 根据入口边界条件,按照经验值给出各个节点t+1时刻的速度迭代初始值u0、压力迭代初始值p*、温度迭代初始值T。此处经验值取值不影响计算结果,只影响收敛速度。根据状态方程和p*、T计算出t+1时刻各个节点的蒸汽密度ρ、比焓h、动力黏度μ。

③ 由各个节点的u0和p*,根据式(20)～(27)计算离散的动量方程式(19)中的系数。方程系数的计算式中ut+1、pt+1、ρt+1代入的参数即为步骤②中给出的迭代初始值u0、p*、ρ。

⑤ 利用各个节点的p′及式(41)求出各个节点的速度修正项u′,并与第③步求解出的各个节点的u*进行叠加,得到修正后各个节点的蒸汽速度u。

⑥ 将以上步骤得到的各个节点的p和u代入式(58)～(65),求解离散的能量方程。由于采用一阶迎风格式,能量方程的求解和动量方程类似,可以由入口边界起逐一计算各个节点的方程系数和比焓h。求出各个节点的h后,根据状态方程求出各个节点的新的蒸汽温度T、蒸汽密度ρ、蒸汽动力黏度μ等。

⑦ 此时的压力p和速度u满足连续性方程,但不一定满足动量方程,因此将本次迭代得到的这一组各个节点的p、u、T、ρ、h、μ作为第②步的迭代初始值,重复步骤③～⑥,直至动量方程、连续性方程和能量方程都收敛,收敛条件为本次迭代与上次迭代结果的相对差值小于10-5,此时各个节点的p和u同时满足连续性方程及动量方程。此时,计算完成,得到t+1时刻各个节点的p、u、T、ρ、h、μ。

⑧ 若边界条件随时间变化,则计算t+2时刻时,代入更新后的边界条件,和t+1时刻的计算结果,重复上述步骤②～⑦。以此类推,直至计算出每一个时间节点的p、u、T、ρ、h、μ。

以上,完成整个方程的计算。

2.4 实验验证

蒸汽管网的水力、热力工况表现为管网中蒸汽温度和压力的分布,选择天津某典型蒸汽管网稳定运行阶段内各热力站和用户的流量以及热力站压力、温度监测数据对模型进行验证。典型管网的管道采用架空布置,经过用户门前或者路口时进行埋地处理。整个管网按照区域划分为4条管道,管网拓扑结构见图2。管道总长7.1 km,供热面积2.1 km2,热源与最远热用户22距离3 808 m。采用上述模型和管网的水力计算模型结合,计算各位置的蒸汽压力和蒸汽温度。

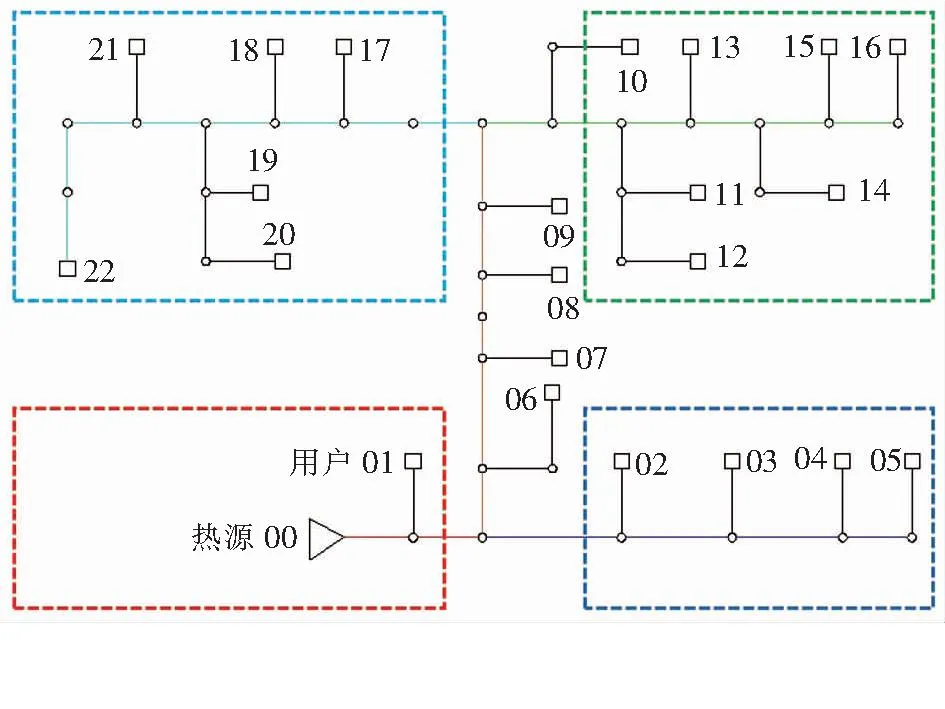
图2 典型蒸汽管网拓扑结构

由蒸汽管网水力热力耦合模型计算结果与实测数据对比可知,所有位置的模型计算值与实测值都较为接近,且离热源越近的位置模拟值与实测值误差越小,这是由于随着热用户与热源距离增加,沿途未被考虑的影响蒸汽管网运行的因素逐渐增加。除个别位置外,模拟值和实测值的相对误差保持在±8%以内,蒸汽温度相对误差绝对值的平均值为3.85%,蒸汽压力相对误差绝对值的平均值为2.15%,说明本文建立的蒸汽管道动态模型计算结果可靠。

3 蒸汽管道动态水力热力计算分析

在实际运行过程中,室外条件会发生变化,蒸汽参数会发生变化,还会对阀门进行调整。因此,本文对蒸汽管道非稳态工况的选取考虑了3种实际情况,分别为环境温度的变化、热源温度的变化、阀门调整导致的管道入口蒸汽压力的变化,相关计算参数见表5。

表5 相关计算参数

3.1 环境温度的变化

在蒸汽管网实际运行过程中,环境温度是周期性变化的,而且不同的地理区域和季节,温度变化幅度不同,有些地点的全天温度变化幅度可达10 ℃以上。选取天津冬季某日的逐时环境温度变化作为非稳态变化项,探究其对蒸汽管道内蒸汽参数的影响。在保证表3中其他参数不变,环境温度周期性变化的情况下,管道出口蒸汽温度(简称出口温度)变化见图3。可以看到,出口温度的变化相对于环境温度的变化有一定的延迟。对于算例中1.649 km的蒸汽管道,管道出口蒸汽温度变化延迟时间约为1.5 h。

图3 环境温度变化对出口温度的影响

实际的蒸汽管道管径各不同,保温层厚度也有一定的差异。为探究蒸汽管道不同传热系数对出口温度变化的影响,模拟了不同的传热系数下出口温度变化,见图4。不同传热系数下,出口温度随时间的变化规律基本一致,但变化幅度产生了较大变化,传热系数越大,出口温度变化幅度越大。通过以上分析,可以得到这样的结论:在环境温度发生变化的情况下,传热系数的变化对出口温度的影响体现为出口温度变化幅度的变化。

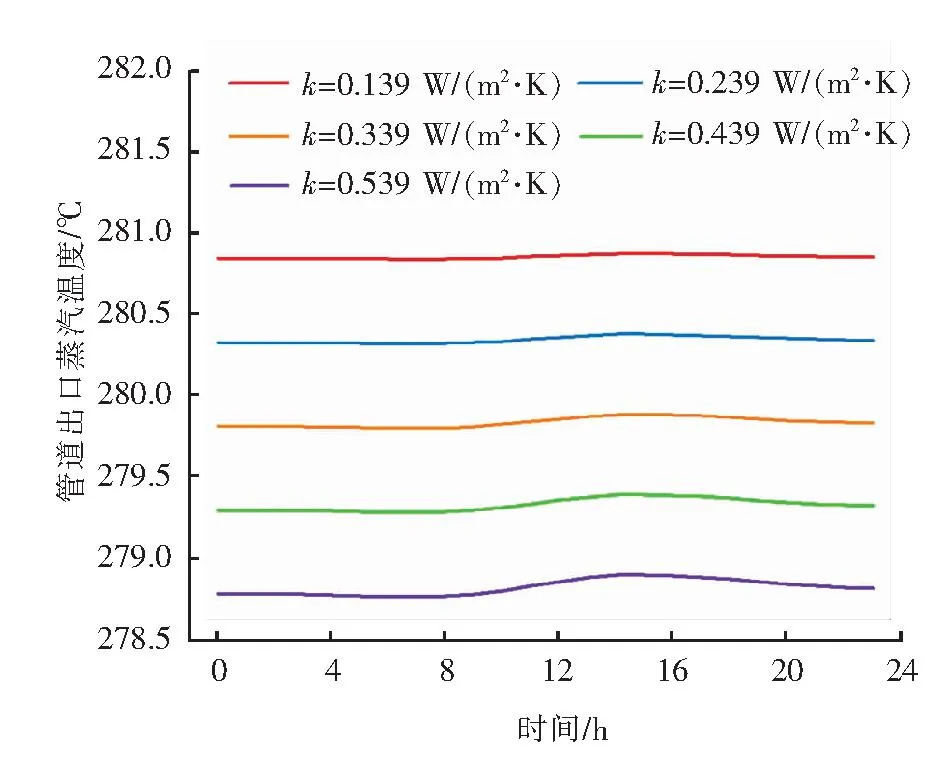
图4 不同传热系数下环境温度变化对出口温度的影响

3.2 管道入口温度的变化

在蒸汽管网运行过程中,由于负荷变化或者环境温度变化,需要在热源处提高或者降低蒸汽温度。热源处的温度变化会传递到管道的不同位置,导致温度或者压力的变化。与热源距离不同,其热滞后性也不相同。在保证表3中其他条件不变的情况下,使管道入口蒸汽温度(简称入口温度)在50 s内上升50 K,管道出口蒸汽温度和管道出口蒸汽压力(简称出口压力)变化见图5。可以看出,入口温度变化会导致出口温度变化,且出口温度变化存在一定的延迟。本案例中1 649 m的管道,出口温度变化延迟时间大约为130 s。出口压力也会受到入口温度变化的影响,在提高入口温度的同时,出口压力瞬间降低,几乎不存在延迟。但由于出口温度存在延迟变化,导致密度的延迟变化,出口压力也会慢慢升高,达到新的稳态。出口压力变化延迟时间与出口温度变化延迟时间基本相同。在这个过程中,出口压力达到的最低值低于最终达到稳态的压力。

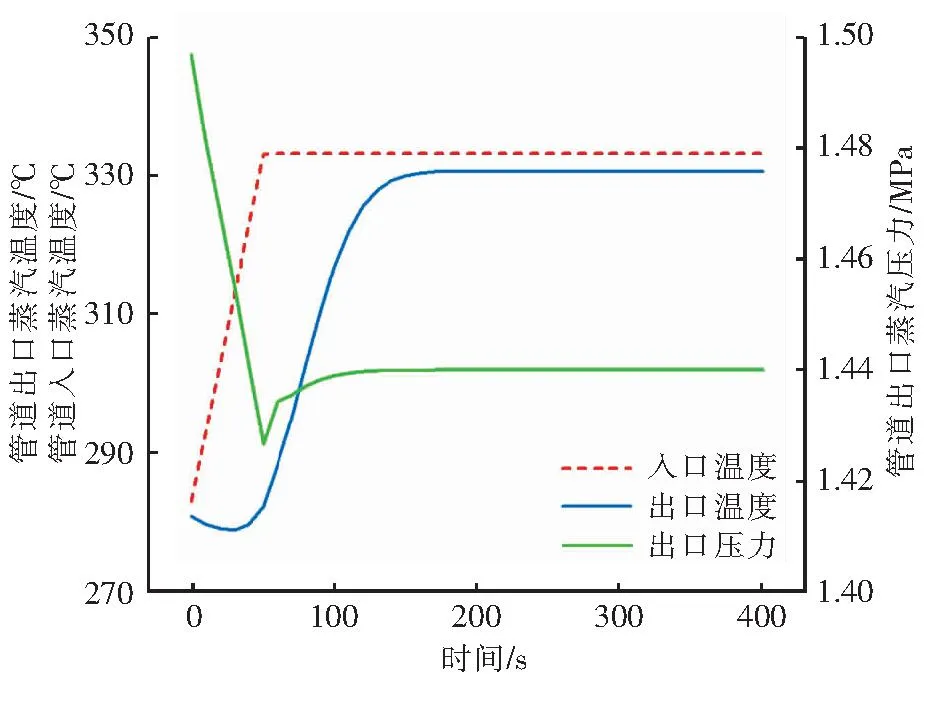
图5 入口温度变化对出口压力及出口温度的影响

温度波在管道内传递比压力波慢得多,沿管道的温度传播存在时间延迟和幅度衰减现象。为探究管道长度对出口温度变化延迟时间的影响,改变了上述算例的蒸汽管道长度,分别变为原长度(记为L)1 649 m的1/4、1/2、3/4,并进行了模拟,结果见图6。管道长度不同,延迟时间不同,管道长度为0.25L、0.5L、0.75L、L的出口温度变化延迟时间分别为50、75、100、130 s,即管道长度每增加约400 m,出口温度变化延迟时间增加25～30 s。

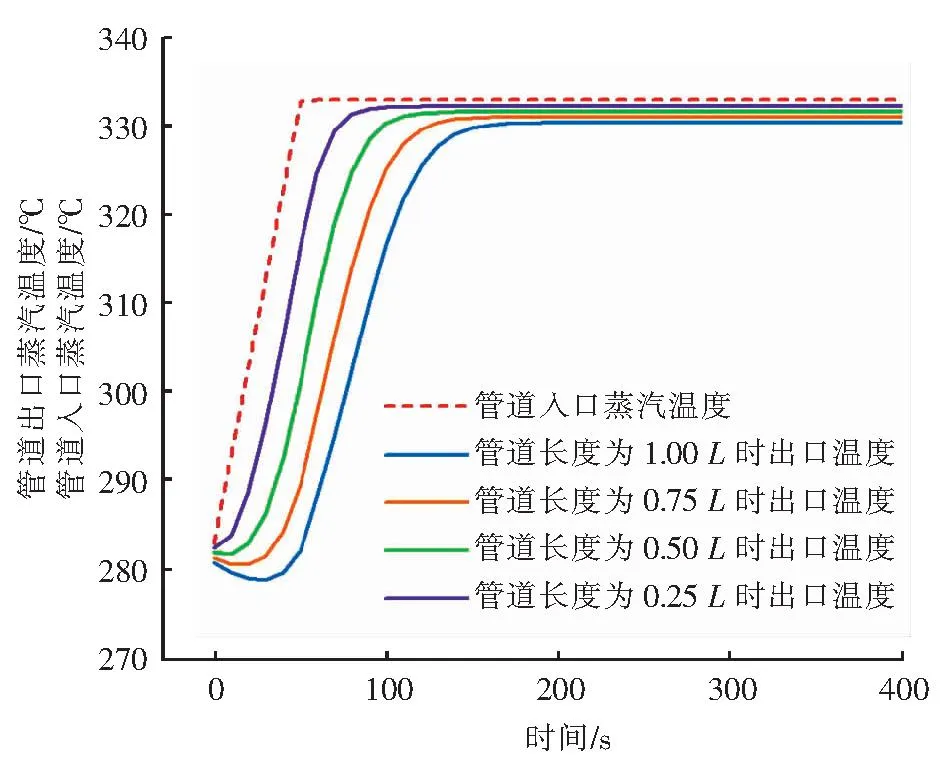
图6 不同管道长度下改变入口温度对出口温度的影响

3.3 管道入口压力的变化

调节蒸汽管网中的阀门时,阀门后蒸汽压力会发生变化,在阀门下游其他位置处的蒸汽状态参数也会动态变化。为了探究调节阀门对下游蒸汽状态参数的影响,在保证表3中其他参数不发生变化的情况下,使管道入口蒸汽压力(简称入口压力)在50 s内下降0.5 MPa,探究入口压力变化对管道出口蒸汽参数的影响。入口压力变化对出口温度和出口压力的影响见图7。

图7 蒸汽管道入口压力降低对出口蒸汽参数的影响

可以看出,随着入口压力降低,出口压力瞬间降低,与入口压力变化保持同步,几乎没有延迟。随着入口压力降低,管道出口蒸汽比焓(简称出口比焓)受压力变化影响,也会发生变化,但其变化过程存在一定的延迟。出口温度变化与出口比焓变化有较大不同,其先是经历了一个与出口压力变化同步的快速下降,然后经历了与出口比焓变化趋势相同的缓慢上升。在入口压力发生变化的阶段,出口比焓未发生明显变化,但是出口压力的变化导致了同等比焓对应的温度发生变化。在入口压力不变的阶段,出口压力不再变化,所以出口温度只受出口比焓的影响。两个阶段不同的影响因素综合作用导致了出口温度的变化。因此,当改变入口压力时,出口压力会同步随之变化,而出口温度会经历两个阶段的变化,第一个阶段与入口压力变化趋势相同且时间上保持同步,第二个阶段变化与第一个阶段变化趋势相反,并逐渐趋于平缓。在出口温度的变化过程中,温度的最小值或者最大值会超过变化的起始值和终止值。因此在实际调控过程中,需要保证设备能够承受温度变化的极值。