波浪补偿舷梯运动学与动力学分析

宋志国,马天宇,魏延辉

(1.南通中远海运船务工程有限公司,江苏 南通 226000;2.哈尔滨工程大学 智能科学与工程学院,黑龙江 哈尔滨 150001)

1 引 言

海上风力储量非常巨大,随着科技的发展,海上风力资源利用逐年增加。风力发电是目前已知的清洁能源之一,具有高效、清洁等特点[1]。与陆地环境相比,海洋环境复杂得多,海上设备在海风、海浪、海流的长时间持续作用下容易产生故障,此时需要维修人员进行登台维修。但因海浪、海流、海风的存在,维修人员不能平稳地到达维修平台,从而产生危险性。

传统的海上作业主要通过直升机、船舶、起重机和吊篮等,但是在经济性和安全性上,传统的方式不尽如人意[2]。随着科技的发展,一种可以补偿海浪运动的舷梯装置提供了一种更加经济、安全的选择。本文主要分析舷梯运动特征,计算其正逆运动学的推导,最后进行运动学的仿真,为补偿控制系统的建立提供理论依据及参考。

2 概 述

正常情况下,风电运维船在工作时会受到海上风浪的影响,在风浪的作用下船体会发生相对运动,主要有横移、纵移、升降、摇摆等复合运动。一般船舶会配置动力定位系统,会对船舶的横移、纵移进行控制,减小运动幅度,但这也仅仅是有限的减小,不能使其达到静止的状态,船舶随着海浪的升降、摇摆运动更是无法控制[3]。

舷梯的工作原理主要是通过监控船舶的运动信号,并将信号传输到控制系统,进而控制舷梯执行机构,从而对船体的升降、摇摆运动进行补偿,并克服运动的耦合性,使海上工作人员和待维修的设备能够平稳安全地转移到维修地点,降低海上工作成本,提高作业效率。舷梯结构如图1所示。

图1 国外某波浪补偿舷梯

波浪补偿模式按照控制方法主要分为3种:被动式补偿、主动式补偿和混合式补偿。

(1)被动式补偿:这种补偿方式结构简单,在现有的装置里面安装补偿装置,两套装置之间没有联系,相互独立。被动补偿设备由随动装置和执行器组成,补偿设备的技术参数根据经验丰富的工人总结的经验设定,其优点是容易实现,技术成熟,基本不消耗能量,但还有一些缺点,如补偿精度不高。在机械设备作业过程中无法对其技术参数进行实时修改,因而几乎无法适应变化莫测的海上工作环境,从而降低补偿工作的高效性,对于比较小的运动变换,反应迟钝。

(2)主动式补偿:运动传感器对船体因受海浪作用而产生的姿态变化进行监测,通过运动学分析,将船体姿态变化量转化成补偿机构所要做的补偿动作信号,再将运动信号传输到执行机构中做出补偿动作(如伸缩运动、旋转运动),对船体姿态变化进行补偿。与被动补偿不同,主动补偿的精度有很大提升,延迟低,但是工作起来十分耗能,不能长时间工作。

(3)混合式补偿:这种补偿方式是前两种补偿方式的混合。在运输过程中,采用主动补偿方式进行高精度的补偿;而在待机期间,使用被动补偿系统,减少能耗,不用中途收回舷梯。这种补偿方式不仅有主动补偿的高补偿精度和安全性,还可以节约没有必要的能源浪费,增加工作时间。

3 波浪补偿舷梯运动学建模

对三自由度补偿舷梯进行模型的建立,主要是对其各个连杆之间的坐标系进行建立,也为之后的高精度舷梯控制装置打好基础。

3.1 舷梯模型简介

本次设计的波浪补偿舷梯(栈桥)主要由俯仰结构、伸缩结构、旋转结构和液压执行单元组成[2]。液压执行单元与旋转结构底座和伸缩结构相连,控制系统通过液压缸的伸缩控制舷梯的俯仰运动,对船舶升沉方向进行补偿。伸缩结构一般是通过齿轮齿条导轨伸缩驱动,为了缓解运动冲击对系统的影响,专门设置了弹簧阻尼系统进行减振。舷梯通过旋转结构的圆柱底座与运维船连接,圆柱底座即是舷梯系统的支撑机构,舷梯系统的回转液压系统设置在此结构内,此系统用于舷梯回转运动及平面内回转补偿。

因为这是一个运动学分析的模拟建模,仅分析舷梯结构三维空间中位置和时间的关系属性,所以在软件中建模不予考虑质量和力学因素,同时忽略管路、阀件、电缆、仪器仪表、栏杆等一些不影响运动学分析的部分,只保留运动主体。

3.2 波浪补偿舷梯运动学模型

三自由度补偿舷梯的结构可以看成是由两个旋转关节和一个伸缩关节组成的三自由度的串联机器人,如图2所示。

图2 舷梯简化模型

D-H参数法的使用对象是两个紧靠的运动连杆,分别编号为i和i-1,然后用矩阵将第i个连杆相对于第i-1个连杆的空间变化表示出来。应用于三自由度补偿舷梯中,可以将舷梯末端相对于底座中心的空间位置关系推导出来。图3为连杆示意图,相关连杆参数如式(1)所示。

(1)

图3 连杆示意图

根据图3所示的相邻连杆的连杆坐标,对三自由度补偿舷梯建立其坐标系,以能更简单地进行求解原则的建立。初始坐标系建立在回转关节底部,绕坐标系O0-x0y0z0的z0轴转动,然后建立坐标系O1-x1y1z1,沿O0-x0y0z0的z0轴方向向上平移到回转关节顶部,平移距离为h1。然后沿着坐标系O1-x1y1z1沿x1轴方向平移到俯仰关节铰点处,并将坐标进行旋转,平移距离为d1,得到坐标系O2-x2y2z2。俯仰关节绕坐标系O2-x2y2z2的z2轴进行旋转,坐标系O3-x3y3z3是坐标系O2-x2y2z2沿着x2方向平移d2距离得到,位置在伸缩关节固定关节末端。三自由度机械臂连杆坐标系如图4所示,D-H参数见表1。

表1 D-H参数表

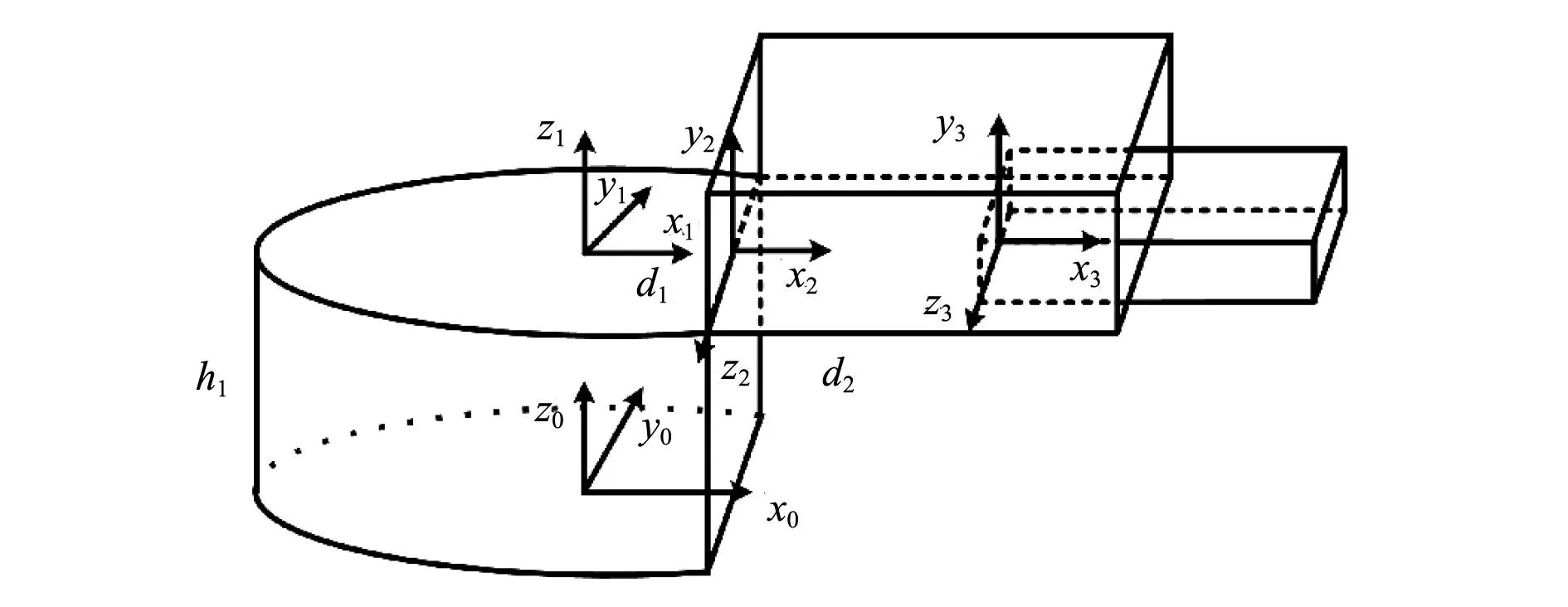
图4 三自由度机械臂连杆坐标系

4 波浪补偿舷梯运动学推导

对波浪补偿舷梯进行运动学分析,主要分为两部分。第一部分是正运动学,已知舷梯回转、俯仰和伸缩关节的角度变化和伸缩变化,求出舷梯末端在起始坐标系下的坐标。第二部分是逆运动学,通过舷梯末端在初始坐标下的坐标,逆向推导出各个关节的变化量[4]。进行正逆运动学的推导是控制波浪补偿舷梯的一个重要前提。

4.1 补偿舷梯正运动学推导

RPY(φ,θ,φ)是补偿舷梯相对于补偿舷梯基底的旋转矩阵。

RPY(φ,θ,φ)=Rot(z,φ)Rot(y,θ)Rot(x,φ)

(2)

式中,φ为补偿舷梯绕z轴旋转量;θ为补偿舷梯绕y轴旋转量;φ为补偿舷梯绕x轴旋转角度;cφ=cosφ,sφ=sinφ,cθ=cosθ,sθ=sinθ,cφ=cosφ,sφ=sinφ。

(3)

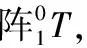
(4)

(5)

(6)

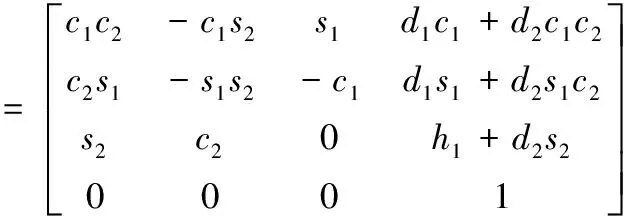
(7)

根据式(7),在O3-x3y3z3上的点位(x3,y3,z3)换成O0-x0y0z0的点位(x0,y0,z0):

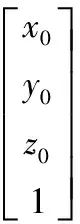
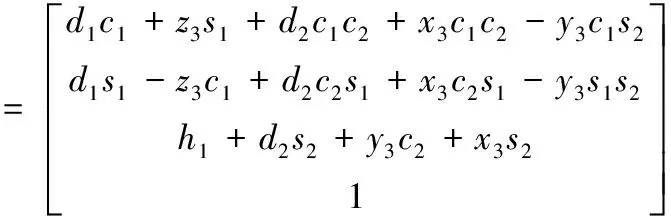
(8)

舷梯末端的位置坐标在坐标系O3-x3y3z3的坐标是(d3,0,0),d3为伸缩梯的活动长度。将(x3,y3,z3)(即(d3,0,0))代入式(8)中可得:

(9)

4.2 补偿舷梯逆运动学推导

逆运动学在舷梯里面是指当舷梯末端达到一个位置,其驱动系统应该做出什么样的变化。即已知舷梯末端在O0-x0y0z0的坐标(x,y,z),求d3,θ1,θ2。可以根据几何方法进行逆运动学的解算,图5是舷梯的几何构图。

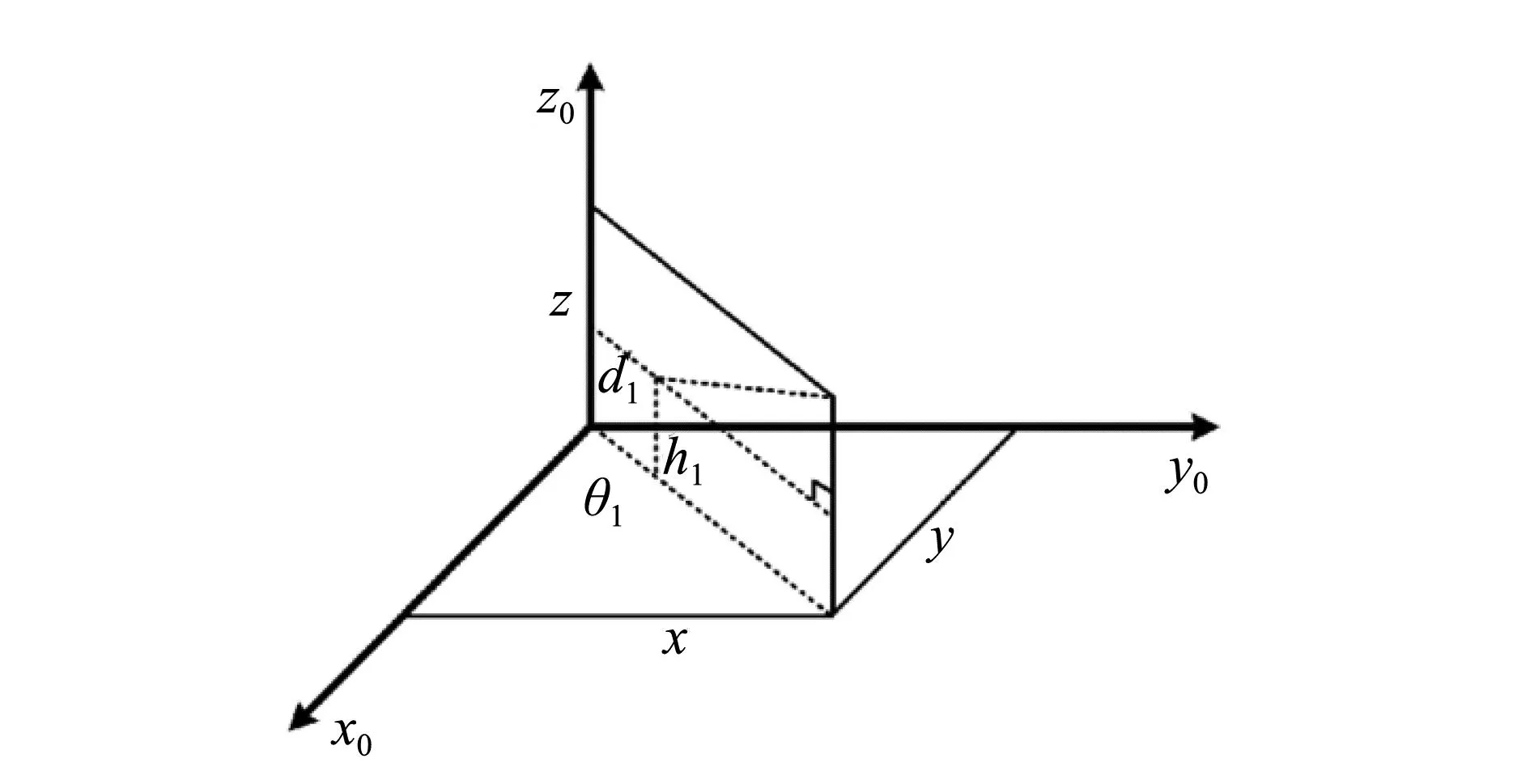
图5 舷梯几何构图

(10)

(11)

(12)

Matlab仿真结果图6所示,通过robotics toolbox工具箱对串联舷梯进行参数设定,从而控制3个自由度关节运动,最后显示舷梯末端位姿状态,验证运动学建模的准确性。将波浪补偿舷梯的参数输入到组件中后,可以在运动空间里面得到其末端活动范围。

图6 Robotics Toolbox中舷梯运动学模型

5 波浪补偿舷梯动力学分析

动力学分析主要是求出补偿舷梯运动时,不同动作产生的力和力矩大小。因为补偿舷梯是三自由度,结构简单,所以可以采用牛顿-欧拉法来进行动力学分析。

对于转动关节归纳如下[5]:

(1)向外迭代计算

(13)

(14)

(15)

(16)

得到力和力矩:

(17)

(18)

(2)向内迭代计算

(19)

(20)

(21)

对于移动关节归纳如下[6]:

(1)向外迭代计算

(22)

(23)

(24)

(25)

得到力和力矩:

(26)

(27)

(2)向内迭代计算

(28)

(29)

最终可以得到力矩公式:

(30)

在求动力学之前,需要将波浪补偿舷梯的结构进行简化处理。假设坐标系O2-x2y2z2和坐标系O3-x3y3z3下的固定部分和伸缩部分的质心在X轴上,为:

(31)

(32)

舷梯伸缩固定部分和滑动部分的转动惯量为:

(33)

(34)

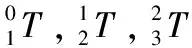
(35)

式中,1R0=(0R1)T,2R1=(1R2)T,3R2=(2R3)T。

设h1,l1,l2分别为俯仰轴高度、伸缩梯固定部分的长度、伸缩梯滑动部分长度,m1,m2分别为伸缩梯固定部分和伸缩梯滑动部分质量。根据图4中建立的坐标系,有:

0P1=[0,0,h1]T

1P2=[d1,0,0]T

2P3=[d2,0,0]T

3P4=[l2,0,0]T

(36)

为了方便计算,假设舷梯忽略其他的力,如摩擦力、风载、雪载、重物等。通过式(31)-式(36),代入到牛顿-欧拉动力学公式中,计算补偿舷梯在补偿运动中所需要的外力和力矩。

(37)

(38)

(39)

(40)

(41)

6 结束语

本文对海工装备用三自由度波浪补偿舷梯的运动学和动力学进行分析,首先建立运动模型,设定坐标系,方便利用D-H参数法推导其正运动学和逆运动学。将结果输入Matlab软件,通过Robotics Toolbox验证运动轨迹。在动力学中,使用牛顿-欧拉法求连杆的力与力矩,求出舷梯做补偿运动所需的力和力矩,为后续对执行器的控制提供参考。