基于DIC与NExT-ITD的结构运行模态测试新方法
2024-01-03蔡子峥徐飞鸿
李 君,蔡子峥,徐飞鸿
(1.桥梁结构安全控制湖南省工程实验室(长沙理工大学),湖南 长沙 410114;2.长沙理工大学 土木工程学院,湖南 长沙 410114)
1 引 言
运行模态分析(Operational Modal Analysis,OMA)作为研究结构在服役阶段动力特性的常用技术[1],其特点是仅已知或仅利用结构振动的响应信号进行模态分析。借助环境激励的运行模态分析方法,因其无需施加和测量激励信号,具有操作简便、费用低廉、不影响结构的正常使用以及适合工程现场环境等特点,近年来得到了快速发展[2]。
作为环境激励下结构模态参数识别的常用方法,自然激励技术(Natural Excitation Technique,NExT)由James等[3]提出,其主要原理是利用结构在环境激励下两测点之间的互相关函数与脉冲响应函数具有相似的数学形式,以互相关函数代替脉冲响应函数进行结构模态参数的识别。Ibrahim时域法(Ibrahim Time Domain,ITD)是由Ibrahim等[4]提出的一种基于结构自由振动响应信号进行模态参数识别的方法。利用自然激励技术对结构响应信号进行前处理,再由Ibrahim时域法即可进行模态参数识别。
然而,在实际工程的模态测试中,多采用加速度传感器测量结构响应信号[5]。但加速度传感器价格偏高、布置繁琐、易受到工程现场恶劣环境的影响,在经济性、易用性、识别精度和抗干扰能力等方面表现不够理想,其应用受到较大限制[6]。数字图像相关方法[7](Digital Image Correlation,DIC)作为一种非干涉光学测量方法,为典型的全场非接触式测量,同时具有测量环境要求低、操作便捷等优点,可以快速获取物体表面的位移信息[8]。
本文介绍了一种基于DIC和NExT-ITD相结合的结构运行模态测试方法。模拟结果与试验结果表明,该方法可以根据散斑图像直接识别出结构模态频率与振型,仅需一部工业相机即可完成测试。模态参数计算直接在时域内进行,无需转换到频率域,计算效率较高,满足工程环境下结构模态测试的需要。
2 基本原理
2.1 数字图像相关方法
DIC通过对结构变形前后表面光强分布的灰度矩阵进行相关运算,从而计算变形结构表面的位移和应变[9]。如图1所示,以位移测点在参考图像子区中的对应点P为中心,以合适像素大小为计算窗口;在变形后图像中,通过预定义的相关系数进行相关计算,寻找变形后图像子区的中心点P′,即可计算出变形前后的整像素位移。对于亚像素位移的计算,采用计算效率、精度和抗噪能力均较为适中的梯度法[10]。
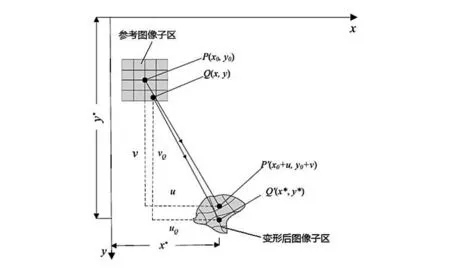
图1 变形前后图像子区示意图
2.2 NExT-ITD
NExT-ITD方法是将自然激励技术和Ibrahim时域法相结合的一种模态参数识别方法[11]。将结构简化为N个自由度的线性时不变系统,设在结构k点施加单位脉冲力,i点的脉冲响应hik(t)为:
(1)
式中,φir表示第i测点的第r阶模态振型;akr表示与激励点k和模态阶次r有关的常数项。
若在结构k点施加环境激励fk(t),在i和j点分别测得响应xik(t)和xjk(t),将环境激励视为理想白噪声时,二者之间的互相关函数可表示为:
(2)
式中,bjr为仅与参考点j和模态阶次r有关的常数项。
式(1)与式(2)具有相同的数学表达形式,二者的模态振型具有相同的特性,故以互相关函数代替脉冲响应函数进行模态参数的识别是可行的。
若采样频率f=1/Δt,则黏性小阻尼线性结构在第t时刻的自由振动观测响应X(t)可由观测模态Ψr叠加表示为:
(3)
式中,ωr为第r阶固有频率,μr=exp(ωrΔt)。
通过延时构造两组矩阵:
(4)
(5)
由式(3)可得:
D=ΦU
(6)
(7)
式中:
(8)
结构模态矩阵Ψ=[Ψ1Ψ2⋅⋅⋅]为特征向量矩阵Φ的上三角部分。
由式(6)与式(7)可得特征方程:
AΦ=ΦΛ
(9)
式中,A为方程AD=的最小二乘解。
为提高计算精度,A取双最小二乘形式[12],表示为:
(10)
显然,矩阵A的特征值和特征向量分别对应μr和Φ,则系统的第r阶固有频率ωr与阻尼比ξr为:
ωr=|lnμr|/Δt
(11)
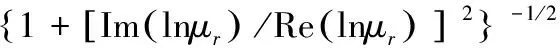
(12)
结构的模态振型通过计算留数确定。设测点i的第r阶留数为Sri,有:
UTS=X
(13)
式中:
(14)
若m为同一阶模态留数中绝对值最大的测点,则对应第r阶模态的归一化振型向量可以表示为:
{φr}=[Sr1Sr2…]T/Srm
(15)
2.3 结构运行模态测试新方法
通过将DIC与NExT-ITD方法相结合,利用DIC取代接触式测量方法,在时域内进行模态参数识别,该方法的流程如图2所示。
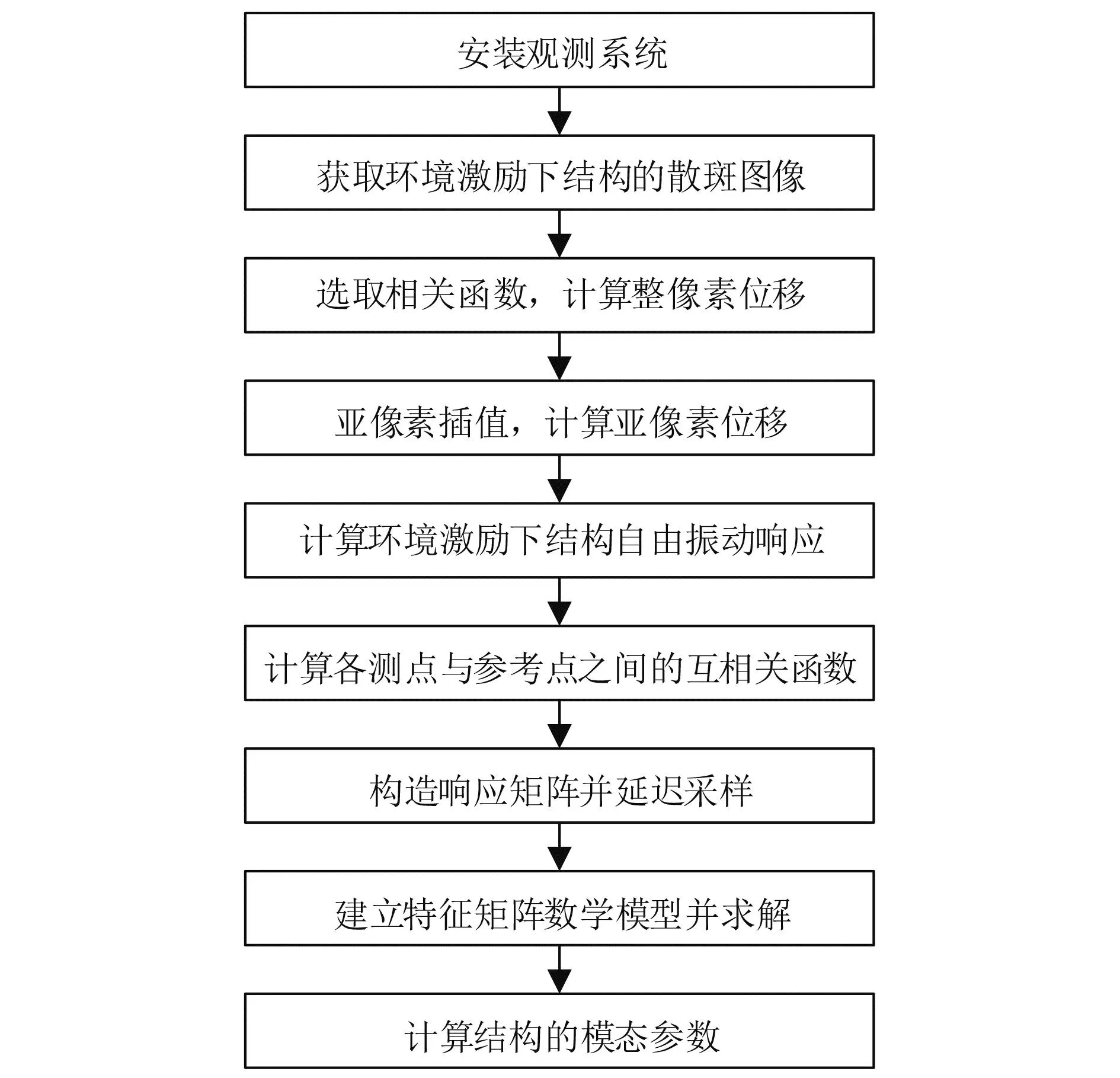
图2 方法流程图
3 模拟结果与分析
为了验证本文提出的新方法,采用ANSYS有限元软件模拟一简支梁模型,对其进行模态频率与振型的识别。简支梁有限元模型如图3所示,其几何及力学参数如下:跨度L=12.0m,截面尺寸b=h=0.1m,弹性模量E=80GPa,密度ρ=7850kg/m3,泊松比μ=0.3。共布置14个测点,其中第11号测点为NExT的参考点。

图3 简支梁有限元模型
利用MATLAB生成采样频率为1000Hz、采样时长为10s的白噪声。将白噪声视为平稳环境激励施加于简支梁模型,通过ANSYS有限元软件分析各测点的位移响应[13]。
通过数值模拟生成仿真散斑图,将各测点的位移响应转换为仿真散斑图。散斑图大小为256×256pixel,标定系数为1mm/pixel。同时向生成的仿真散斑图中添加均值为0、方差为10-2的高斯白噪声。测点7在t=1s时刻的原始散斑图与加噪后的散斑图如图4所示。

(a) t=1s时刻原始散斑图 (b) t=1s时刻加噪后散斑图
通过DIC,由仿真散斑图计算各测点的位移响应,将此信号作为“实测信号”,将ANSYS有限元分析的模型位移响应信号作为“原始信号”。测点7的原始信号与实测信号如图5所示,由图5可以看出,DIC具备良好的测量精度与抗干扰能力。因此,在实际工程测试中,用该方法取代接触式测量具有一定的可行性。
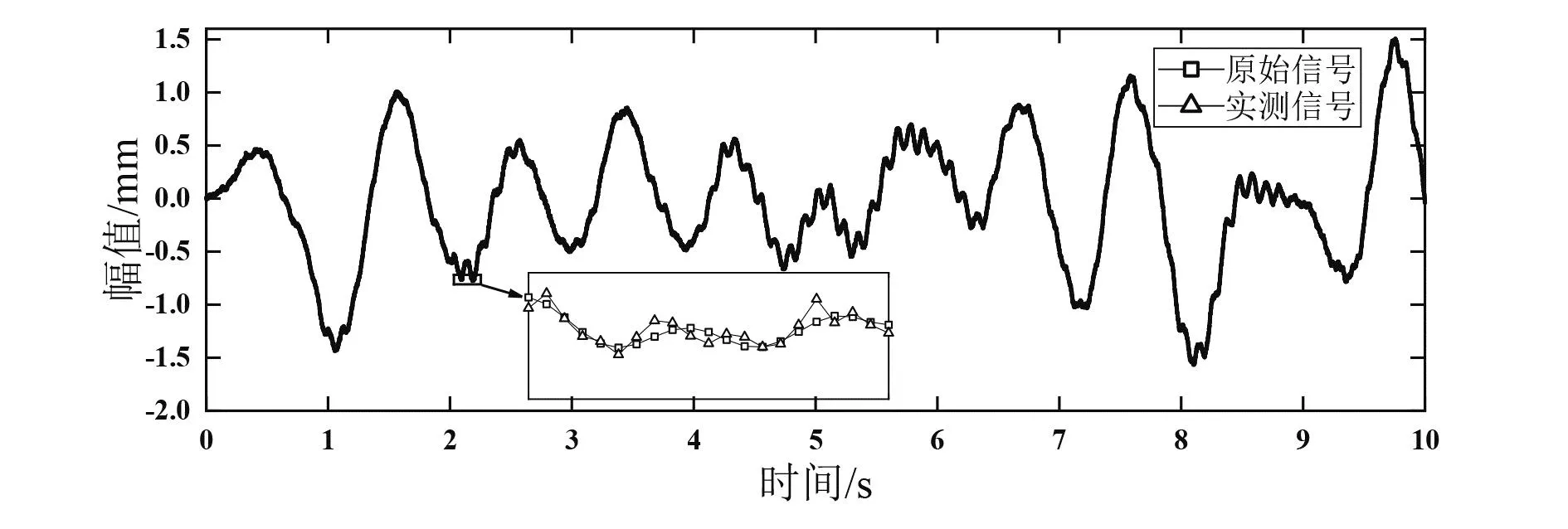
图5 测点7的原始信号与实测信号
定义相对误差为[(识别值-理论值)/理论值]×100%,简支梁模型的前5阶频率理论值与识别值的相对误差见表1,振型如图6-图10所示。
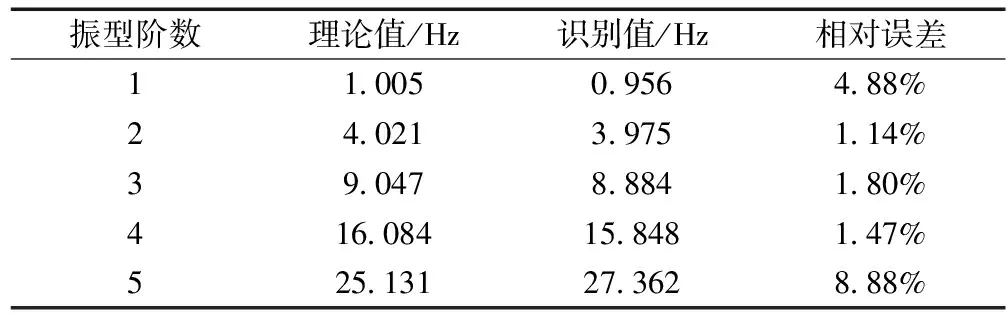
表1 频率理论值与识别值
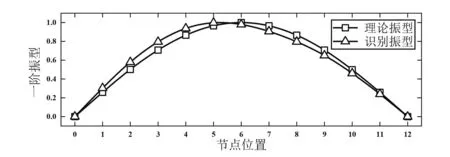
图6 1阶理论振型与识别振型
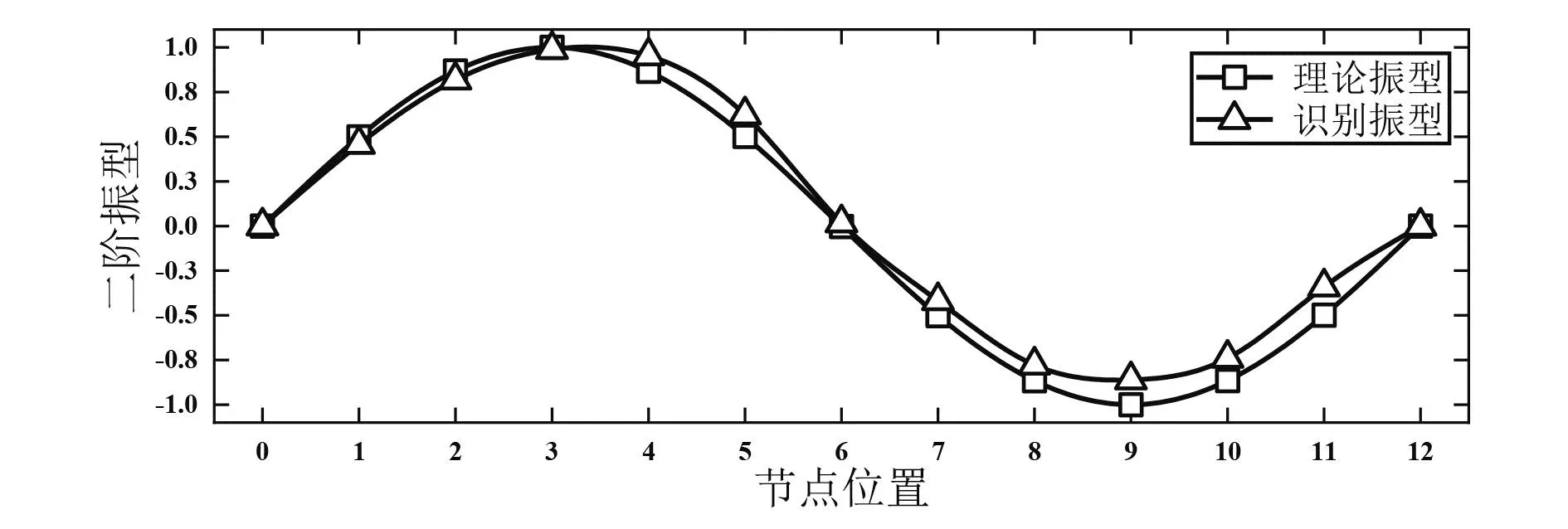
图7 2阶理论振型与识别振型

图8 3阶理论振型与识别振型
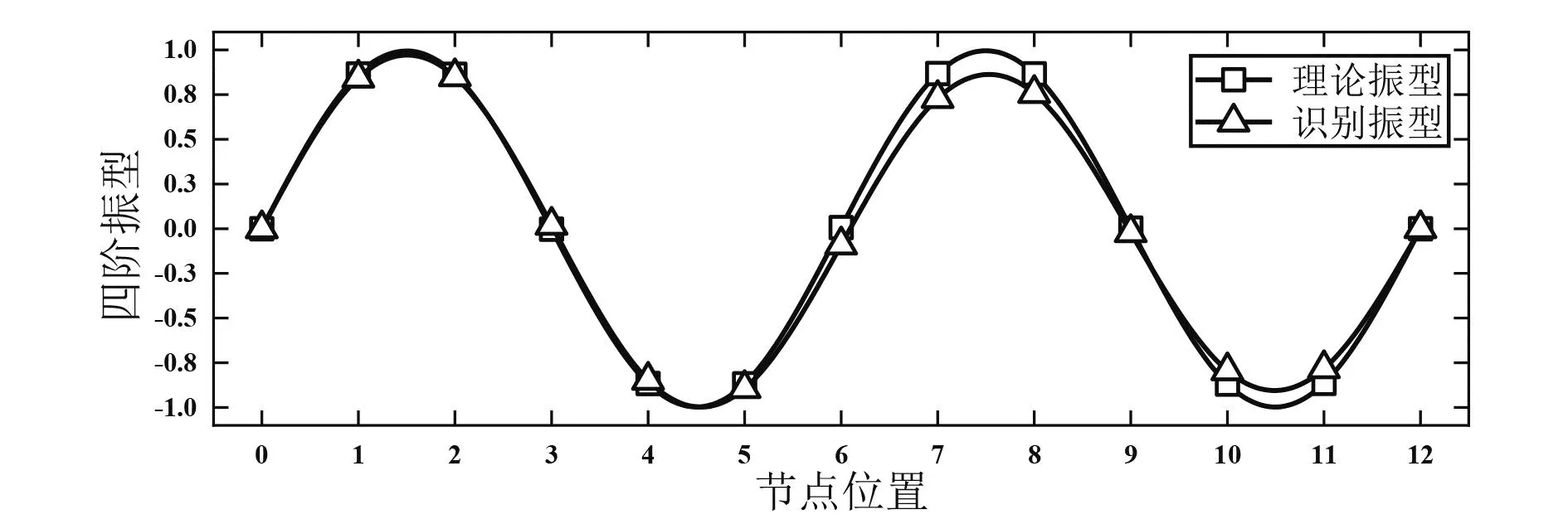
图9 4阶理论振型与识别振型

图10 5阶理论振型与识别振型
由表1的数据对比可以发现,本文提出的新方法在识别前4阶频率中最大误差仅为4.88%。由图6-图10可以看出,前4阶振型识别误差较小,但对于第5阶振型的识别出现了较大的误差。结合表1可以发现,该方法对于高阶次模态参数识别的误差较大,这是由于环境激励状态不同于试验状态模态分析,无法设计激励能量与激励形式,可能对结构的激励不充分,从而导致部分高阶次的模态参数难以识别。
4 试验结果与分析
以某裂缝混凝土简支梁为试验对象,分别采用本文提出的新方法与基于加速度传感器的方法对其进行模态频率与振型的识别。该混凝土梁的跨度L=100cm,截面尺寸b=10cm,h=15cm。由于梁刚度相对较大,主要测试其在竖直平面内的弯曲模态。新方法的测量系统如图11(a)所示,沿梁轴线方向共选取11个测点,采用NX3-S4型工业相机(最大分辨率1280×1024,最高帧率3750fps)进行散斑图像拍摄。为提高识别精度,每3个测点作为一组进行数据采集,每组采集时长为10s。各测点在t=1s时刻的散斑图如图11(b)-图11(d)所示。
同时利用如图12所示的PULSE多分析仪系统对该混凝土梁进行测试,沿梁轴线方向共选取15个测点。现场测试利用8个传感器分2组进行,数据采集时长为30s,并利用PULSE系统自带的分析软件进行OMA分析。

图12 PULSE多分析仪系统
试验测得该混凝土梁的前3阶频率如表2所示,振型如图13-图15所示。

表2 混凝土梁的前3阶频率
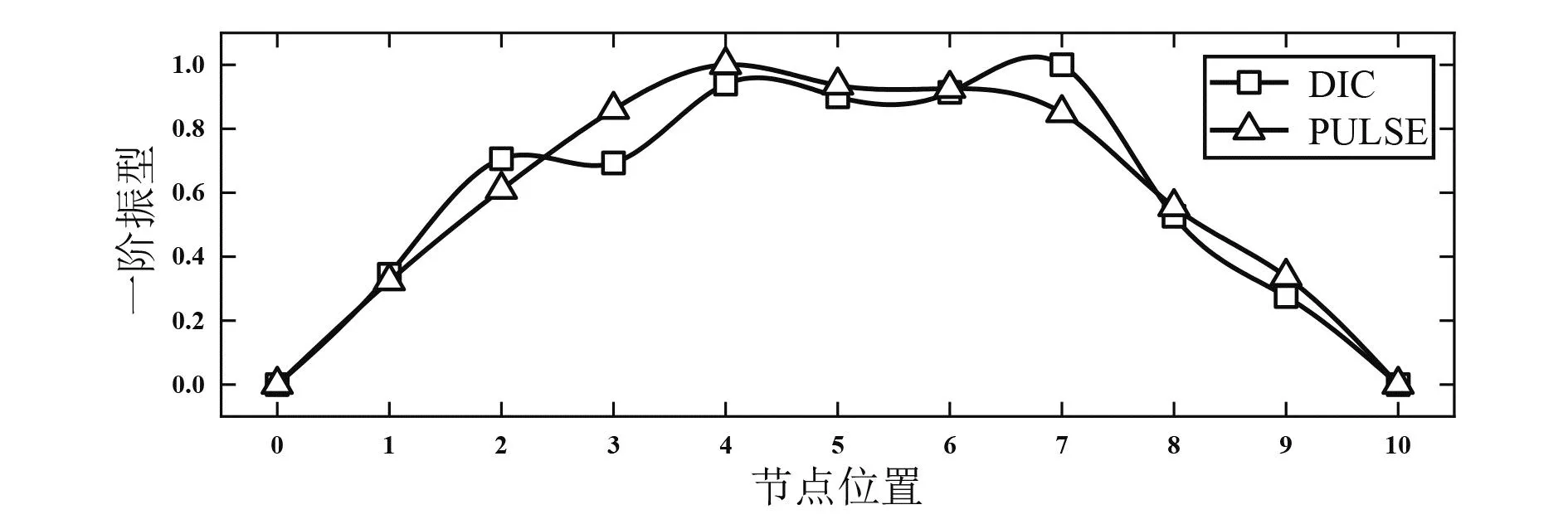
图13 混凝土梁的1阶振型
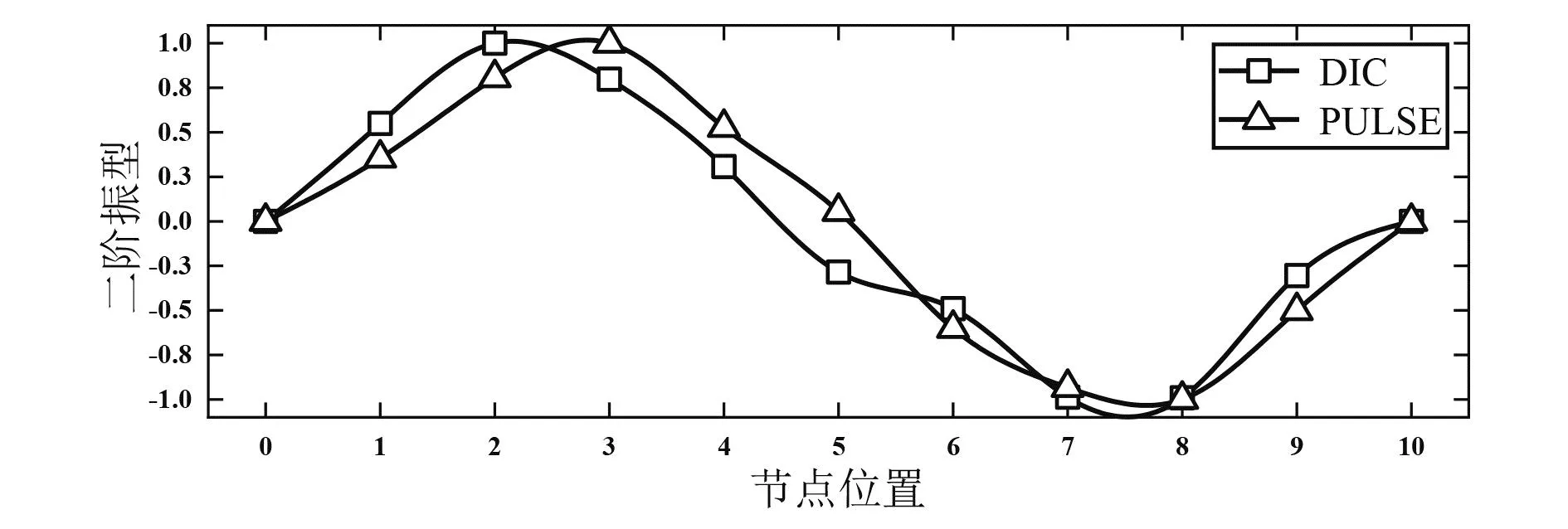
图14 混凝土梁的2阶振型

图15 混凝土梁的3阶振型
由表2的数据对比可以发现,本文提出的新方法对于混凝土简支梁的低阶频率识别精度较高。与PULSE系统相比,该方法在实现了非接触式测试的同时,识别前3阶频率时最大误差为9.84%。同时结合图13-图15可以发现,该方法对于振型的识别效果较好,识别精度可以满足工程测试需要。
5 结束语
本文将DIC与NExT-ITD相结合的方法应用于结构运行模态测试中,充分发挥了数字图像相关方法全场非接触式测量的优点,仅需一部工业相机便可完成对结构的模态参数识别。同时,该方法在时域内进行模态参数的计算,回避了傅里叶变换处理,避免了信号泄漏、分辨率降低以及旁瓣等因素对识别精度的影响,且提高了计算效率。数值模拟结果与试验结果表明,该方法在考虑测量噪声的情况下仍有较好的适应性,同时与传统OMA的试验结果一致性良好。该方法具备良好的识别精度与抗噪能力,符合工程环境下结构模态测试的需要。
