基于气象数据降维与混合深度学习的短期电力负荷预测

申洪涛,李飞,史轮,孙胜博,杨振宁,杨挺

(1.国网河北省电力有限公司营销服务中心,石家庄市 050035;2.天津大学电气自动化与信息工程学院,天津市 300072)

0 引 言

随着新型电力系统的建设,电网逐步向更加智能化、灵活交互式系统过渡发展[1]。电力负荷预测在电力系统的部署、规划和运行影响重大。精确的短期负荷预测能通过预知用户用电行为指导电网组合优化调度,在维持电力系统的安全与稳定运行的同时,还可以减少化石能源发电成本,减污降碳,并合理引导电力市场及碳市场的运营[2-3]。因此,研究电力短期负荷预测方法,提升预测精度意义重大。

近年来,国内外学者通过不断的研究,推动了短期负荷预测领域发展。常用的短期负荷预测方法主要使用负荷历史数据,通过对其训练提取特征,实现下一时期的预测[4-5]。如采用长短时记忆(long short-term memory,LSTM)神经网络的负荷预测方法[6]、基于经验模态分解的短期负荷预测方法[7]等。但短期电力负荷受多种因素影响,具有波动性大、随机性强的特点。尤其是区域型电力负荷,其包含居民、工业等多种负荷类型,容易受到温度、湿度等气象因素的影响,因此如果能够将气象数据融合考虑,将能够进一步提升短期负荷预测的精度[8]。与此同时,电力广域感知技术的发展也为获取区域气象多参量数据提供了可能[9]。

然而,当高维气象参量数据输入现有机器学习算法中进行训练和预测时,由于弱相关维度数据的混杂,以及数据间线性耦合的影响,往往会导致算法出现过拟合等问题,造成模型失效、预测精度不升反降的弊端[10-11]。针对该问题,本文提出了基于稀疏核主成分分析(sparse kernel principal component analysis,SKPCA)的高维气象数据降维方法,其能够实现对非线性气象数据的降维,且具有重构主成分可解释性强的优点。首先,将高维气象数据降维过程建模为回归优化型问题,并增加L1范数和L2范数组成的弹性网惩罚项以稀疏化回归问题,进而更新选取贡献率集中解释性好的稀疏核主成分进行数据降维。

在获取低维强相关的气象数据基础上,本文提出了基于卷积神经网络(convolutional neural networks,CNN)和LSTM混合深度神经网络的电力短期负荷预测方法。将网络的输入(负荷功率及经过SKPCA降维后的气象数据)组成图像,并将其输入CNN中,通过卷积操作来提取该图像的空间相关特征;然后由LSTM通过相互连接的隐含层结构以及门结构来提取负荷功率数据的时间相关特征,从而全面利用数据的时-空相关性特征,提升负荷功率的短期预测精度。最后,本文选用负荷预测公开数据集,对所提算法进行了实验验证。结果表明,通过SKPCA降维后的气象数据显著提升了区域型电力短期负荷预测精度。

1 基于SKPCA的高维气象数据降维方法

如前所述,区域型电力负荷包含居民、工业等多种负荷类型,容易受到温度、湿度等气象因素的影响。如当环境温度或湿度增加时,制冷和除湿设备的电力负荷将会显著提升。值得注意的是,无论是区域微气象观测,还是从专业气象卫星或数据库获取,气象数据往往呈现高维非线性。研究表明,若深度神经网络的输入为强相关高维,将极易诱发网络过拟合,从而降低系统辨识性能[12]。因此本文首先面对短期负荷预测需求,对高维气象数据采用基于稀疏核主成分的方法实现数据有效降维。

1.1 基于核主成分分析法的数据降维方法

核主成分分析(kernel principal component analysis,KPCA)可以处理多维非线性气象数据[13],降低如温度、湿度、风速等多维非线性数据之间的相关性。假设气象数据的维度为P,每一维的采样点数为N,可以将原始气象数据X表示为xi∈N(i=1,2,…,P)。通过非线性映射将原始气象数据xi映射至高维特征空间φ(xi)。此时,KPCA则转化为对矩阵W进行主成分分析(principal component analysis,PCA)处理。矩阵W的计算公式为:

(1)

为提高计算效率,需要通过W=W-BW-WB+BWB来更新矩阵W(矩阵B中每一个元素都是1/P),从而使φ(x1)、φ(x2)、…、φ(xi)、…、φ(xP)满足:

(2)

然后,基于奇异值分解或者特征值[14]分解计算矩阵W的特征值λk以及特征向量vk,公式如下:

Wvk=λkvk

(3)

将特征向量vk代入W中:

(4)

考虑到vk在高维特征空间中,故vk可以转换为φ(xi)的线性组合,满足:

(5)

式中:aki为φ(xi)转换为vk的系数。φ(x)在vk的映射为:

(6)

式中:k(x,xi)等于φ(x)φ(xi),即为φ(x)和φ(xi)的内积。

最终,重构的核主成分及其方差贡献率为:

X′k=Xvk

(7)

(8)

式中:X′k为第k个核主成分;θk为第k个核主成分的方差贡献率。

通过设定方差贡献率阈值θ(一般设定为95%),可以选择不同数量的核主成分,从而实现数据降维。

1.2 基于稀疏核主成分分析的数据降维方法

然而,由公式(7)可知,核主成分是由原始数据与特征向量vk相乘得到,但是由于vk中并不存在零值,故以vk为重构系数的核主成分将与全部维度的原始数据都呈现相关性,存在难以解释的弊端。

为将vk中系数较小的变量剔除以提高重构主成分的可解释性,本文在KPCA的基础上,提出了稀疏核主成分分析(SKPCA)。首先,将气象数据通过KPCA进行处理,并将降维过程,即公式(7),描述为回归优化型问题,并基于最小二乘法建立求解模型;其次,在求解模型中,增加弹性网惩罚以稀疏化回归系数;最后迭代求取贡献率集中且解释性好的稀疏核主成分,并依据方差贡献率阈值进行降维。

基于预设的方差贡献率阈值θ,选择前K个核主成分,其特征向量为αP×K=[v1,v2,…,vk]。设定原始气象数据简写为X,稀疏回归系数为βP×K=[β1,β2,…,βk],通过最小二乘法求解稀疏回归系数的过程为:

(9)

(10)

式中:λ1和λ2分别为L1范数和L2范数的系数。

设定λ2为常数,通过最小角回归算法[15]求解公式(10),从而得到稀疏回归系数β。考虑到上述算法的结果严重依赖KPCA,所以本文对其改进,提出带弹性网惩罚的稀疏核主成分分析的独立方法[16-17]。

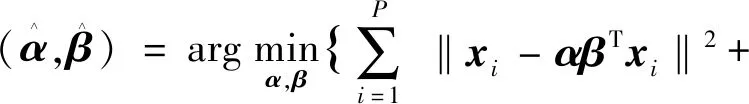
(11)

式中:λ1,k为第k个L1范数系数。值得注意的是,所有K个主成分采用相同的λ2,不同的λ1,k用于惩罚不同核主成分的特征向量。

最终,根据人为设定的方差贡献率阈值θ可以选择对应数量的稀疏核主成分,从而实现高维气象数据的降维。此外,由于弹性网惩罚项的作用,可以将α中系数较小的因素剔除,使得稀疏回归系数β包含了多个零系数,从而令重构主成分只和某些影响较大的气象维度相关,如温度、湿度或气压,更容易解释主成分的构成。

1.3 具体降维步骤

基于SKPCA的数据降维方法步骤如下:

1)中心化高维气象矩阵X,设置方差贡献率阈值θ(本文设定θ=95%);

2)更新公式(1)中的矩阵W,并求取特征值λk和特征向量vk;

3)根据θ选取前k个主成分,从而得到特征向量矩阵αP×K;

4)当m=1,…,K,求取稀疏特征向量矩阵βP×K:

(12)

5)通过XΤXβ=UDVT,并更新α=UVT,其中U、D以及V分别为奇异值分解过程中的左奇异向量、奇异值对角矩阵以及右奇异向量;

6)重复步骤4)和5),迭代至α和β收敛,此时重构的稀疏主成分为Xβ。

2 基于CNN-LSTM的负荷预测方法

在获取低维气象数据的基础上,将网络的输入(负荷功率及经过SKPCA降维后的气象数据)组成图像,并通过CNN的卷积操作来提取负荷功率及气象数据的空间相关特征,通过LSTM相互连接的隐含层结构以及门结构来提取时间相关特征,从而提出基于CNN-LSTM混合深度神经网络的电力短期负荷预测方法全面利用数据的时-空相关性特征,提升负荷功率的短期预测精度。

2.1 基于CNN的负荷及气象数据空间特征提取模块

CNN-LSTM模型的输入为历史负荷功率和KPCA降维后气象数据。该输入仍为多维序列,可以将其拼接为图像,称为负荷及气象图。卷积神经网络(CNN)的特殊结构可以充分挖掘负荷及气象图的空间关系,提取跨域数据间价值特征,从而提高电力负荷预测的精度。此外,为减少参数数量,本文使用leaky整流线性单元(leaky rectified-linear unit,Leaky ReLu)激活函数来非线性映射神经元[18]。CNN包括卷积层、池化层等,其中卷积层负责提取负荷及气象图的空间特征。

2.1.1 基于卷积层的空间特征提取

卷积层可以提取负荷及气象组成图像的特征,其中卷积核是一个包含系数矩阵的小窗口,这个窗口在负荷及气象图上滑动并进行卷积运算,从而提取到图像的空间相关特征[19-20]。卷积层的计算公式如下:

(13)

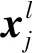
2.1.2 基于池化层的空间特征压缩

为了压缩卷积层特征,池化层可以对负荷及气象序列图的高维空间相关特征进行下采样,转换为CNN层提取的空间相关特征。本文拟采用最大池化方法[21],具体公式为:

(14)

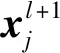
2.2 基于LSTM的时间特征提取模块及预测

以CNN提取的空间相关特征为输入,长短时记忆(LSTM)神经网络可以提取负荷及气象图的时间相关特征,重点关注于负荷序列本身的趋势性和周期性。长短时记忆(LSTM)神经网络借鉴了循环神经网络隐含层相互连接的独特网络结构,保证其可以利用之前时刻的时序信息训练当前时刻的网络,从而有效地提取负荷及相关数据的时间相关特征[22-23]。

设xt为LSTM层的输入,即CNN层输出的空间相关特征;ht为LSTM层的输出,即LSTM层输出的时间相关特征。考虑气象空间特征用于短期负荷预测的长短时记忆单元的结构及连接方式,如图1所示。It、Ft和Ot分别为LSTM单元中输入门、遗忘门、输出门的输出,Ct是细胞状态。遗忘门可以挑选出之前时间节点的有用记忆,输入门可以提取现在时间节点的有用信息,输出门可以整合现在时间节点信息和细胞状态完成输出[24-25]。具体公式如下:

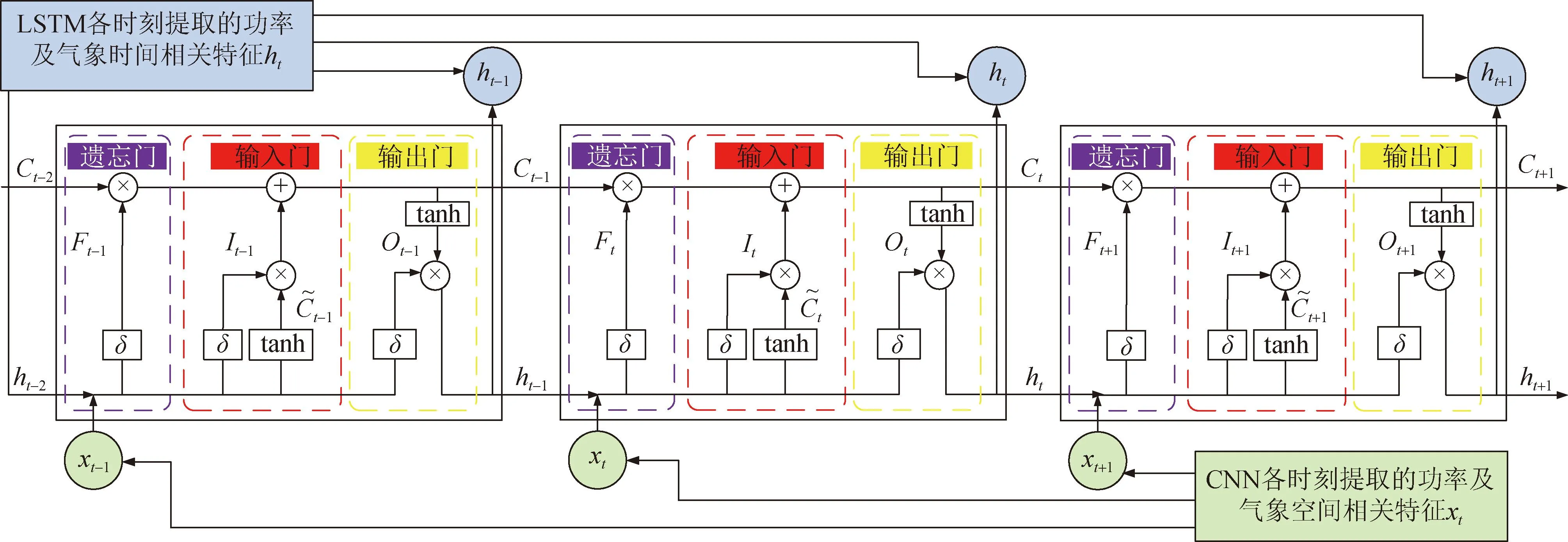
图1 适用于短期负荷预测的长短时记忆单元结构及连接方式Fig.1 The structure and connection method of long short-term memory unit suitable for short-term load forecasting

It=δ(Uixt+Wiht-1+bi)

(15)

Ft=δ(Ufxt+Wfht-1+bf)

(16)

Ot=δ(Uoxt+Woht-1+bo)

(17)

(18)

(19)

ht=Otσ(Ct)

(20)

最终,基于CNN和LSTM提取的时-空相关性特征,使用全连接层[26]进行负荷预测,公式如下:

(21)

最后,给出基于SKPCA和CNN-LSTM的短期电力负荷预测算法全流程图,如图2所示。

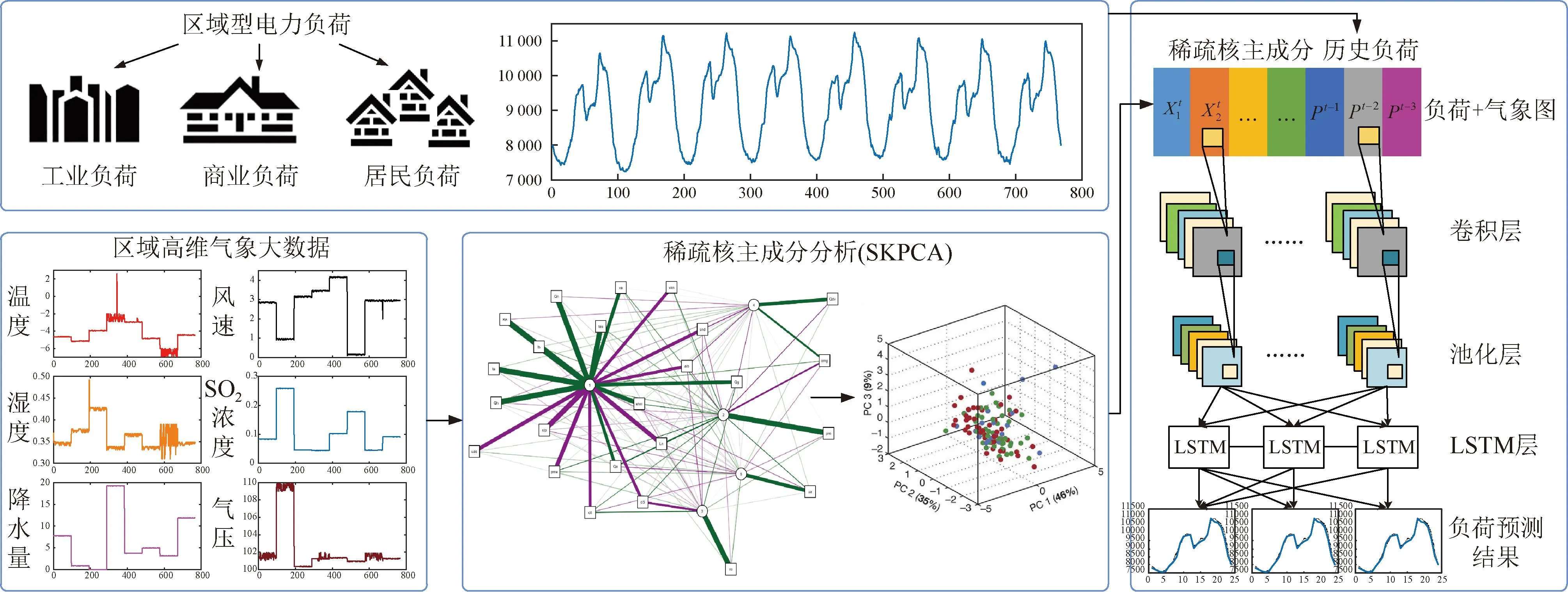
图2 基于SKPCA和CNN-LSTM的短期电力负荷预测算法全流程图Fig.2 The overall flowchart of the short-term power load forecasting based on SKPCA and CNN-LSTM

3 实验及分析

3.1 数据集及评价指标

为测试所提出的基于SKPCA降维和混合深度神经网络的电力短期负荷预测方法的性能,采用实际负荷数据集进行测试。数据来源为于某经济发达地地区实际观测统计数据,种类共8维:除了负荷功率数据(计及该地区工业负荷、居民负荷等总用电负荷)之外,还包括了影响负荷短期波动的7种气象数据,分别为温度X1、湿度X2、风速X3、降水量X4、云量X5、SO2浓度X6、和气压X7。实验采集装置每隔15 min采集一次地区总负荷以及7维气象因素,因此本文实验基于上述数据进行该区域未来15 min的短期负荷预测。

对算法预测精度的评价标准选择平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)三个指标[27-28],计算公式分别如下:

(22)

(23)

(24)

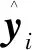
3.2 高维气象数据降维实验及分析

高维气象数据中存在着大量的无关因素,且数据间具有严重的共线性以及群组效应,影响了负荷预测精度的提升,所以应对气象因素开展降维操作以提升数据质量[29-30]。为体现SKPCA的有效性,选取PCA、KPCA作为对比方法,开展对比实验。为了保证实验的合理性,PCA、KPCA和SKPCA都采用了相同的超参数设置,例如累计方差贡献率阈值设定为95%;KPCA和SKPCA选择方差为100的高斯核函数。最终,PCA、KPCA和SKPCA方差贡献如图3、图4和图5所示。

图3 主成分分析的方差贡献率Fig.3 Variance contribution rate of PCA

图4 核主成分分析的方差贡献率Fig.4 Variance contribution rate of KPCA

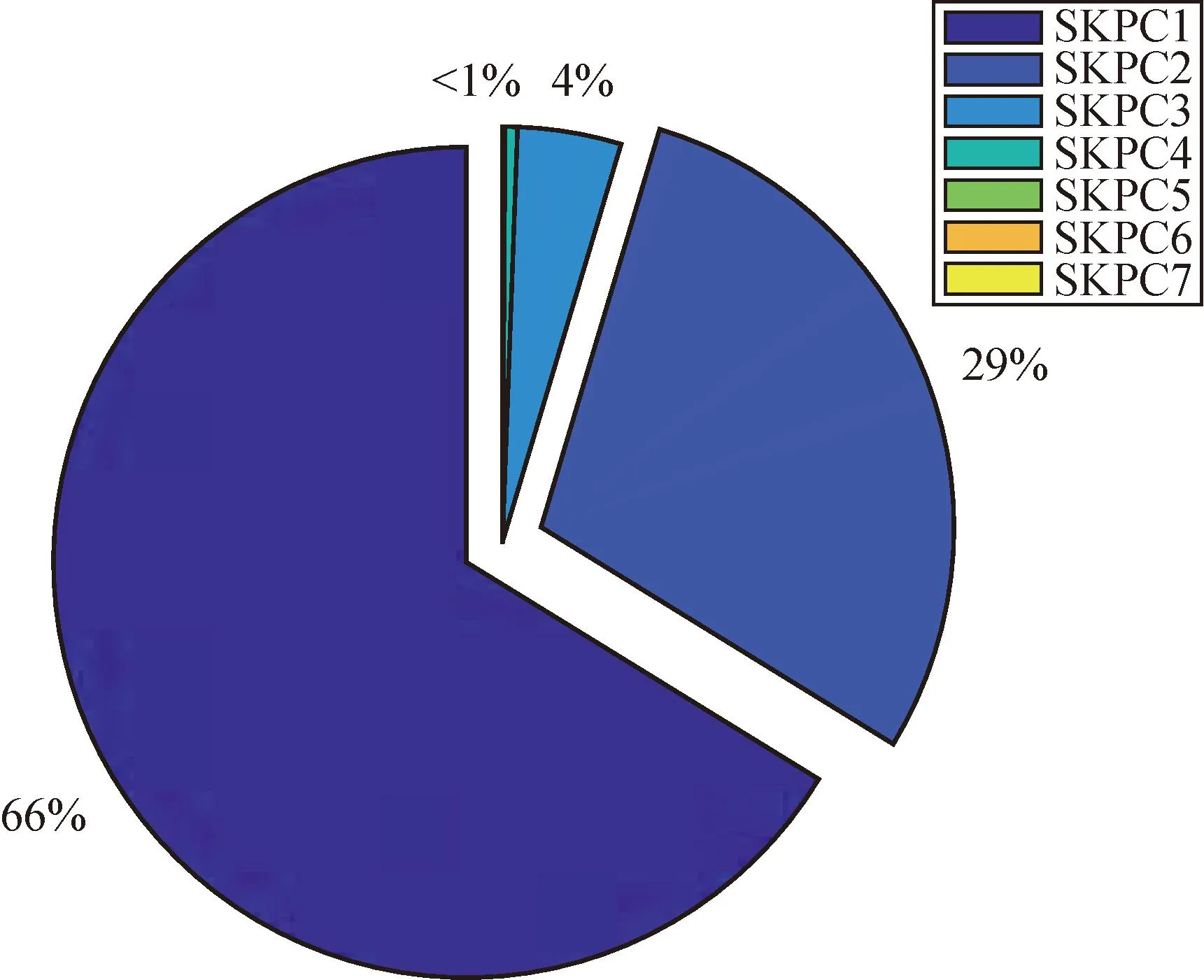
图5 稀疏核主成分分析的方差贡献率Fig.5 Variance contribution rate of SKPCA

由图3—5可知,PCA、KPCA与SKPCA的第一主成分都是各主成分中方差贡献率最大的,分别为41.47%、64.56%和66.32%。此外,依据累计方差贡献率阈值95%,PCA、KPCA与SKPCA分别将7维气象因素降低至5、3和2维。对于方差贡献率过小的主成分应该被剔除,以小于1%为例,PCA、KPCA分别剔除了1个和3个主成分,而SKPCA则有效剔除了4个主成分。综上所述,SKPCA可以用更少主成分表示较多信息,方差贡献率更为集中,即降维效果更好。3种方法的细节如表1、2和3所示,表中PC、KPC以及SKPC分别表示主成分、核主成分以及稀疏核主成分。

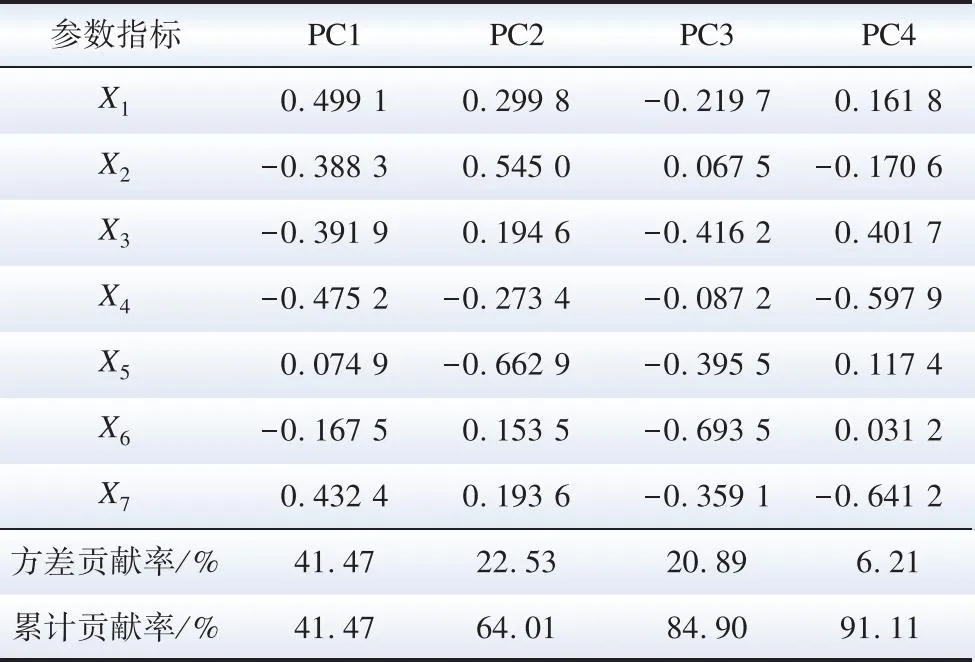
表1 主成分系数及方差贡献Table 1 Coefficient and variance contribution of PCs

表2 核主成分系数及方差贡献Table 2 Coefficient and variance contribution of KPCs

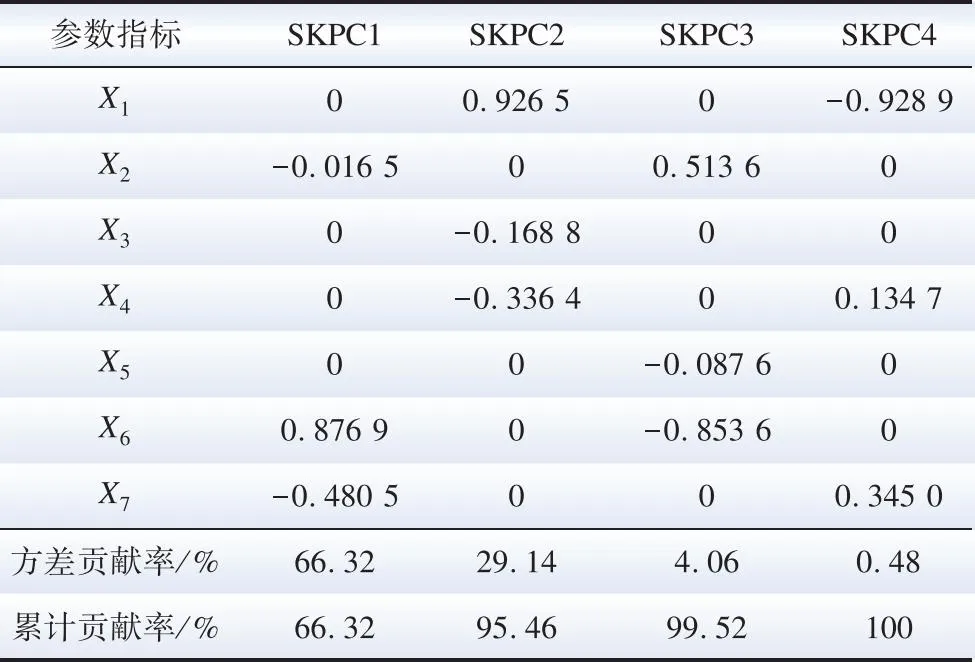
表3 稀疏核主成分系数及方差贡献Table 3 Coefficient and variance contribution of SKPCs

进一步通过表1、2和3结果分析可知,PCA和KPCA的系数并不存在零元素,这意味着经过该系数重构的主成分无法剔除任何一个气象因素,主成分的可解释性较差;由于弹性网惩罚的应用,SKPCA可以将较小的系数精准压缩至0,从而可以以较小的原始气象变量来解释主成分。例如,以第一主成分为例,PCA和KPCA的重构主成分需要7种气象进行解释,而SKPCA则将X1、X3、X4和X5系数压缩为0,这就表明SKPCA的第一主成分只与湿度X2、SO2浓度X6、和气压X7相关,解释性更好。其中SO2浓度X6与当地工业生产排污有密切关系,因此X6与用电负荷呈现强相关。最后,依据累计方差贡献率阈值95%,通过SKPCA可以将7维气象数据降低至2维,前2个稀疏核主成分为:

Y1=-0.0165X2+0.8769X6-0.4805X7

(25)

Y2=0.9265X1-0.1688X3-0.3364X4

(26)

3.3 短期负荷预测实验及分析

3.3.1 降维前负荷预测实验及分析

进一步,对比分析预测算法的性能。在此,为分析气象数据的重要性以及混合深度学习神经网络对非线性拟合的优越性,分别与两类预测模型进行对比:第一类对比预测模型不考虑气象,仅以历史负荷为输入的反向传播(back propagation,BP)神经网络以及LSTM神经网络负荷预测算法;第二类对比预测模型是以历史负荷和未降维气象为输入的CNN神经网络、LSTM神经网络以及CNN-LSTM神经网络为基础的负荷预测算法。5种对比方法的预测结果如表4所示。

表4 不同预测算法结果对比Table 4 Comparison of prediction results of basic models

由表4可知,在第一类不考虑气象数据的对比预测模型中,BP的网络及神经元结构简单,预测精度波动较大且易于陷入局部最优,MAE、MAPE和RMSE分别高达727.69 MW、8.11%和946.67 MW;LSTM_1由于其连接的隐含层结构,使其更适合处理负荷功率等时序数据,预测结果稳定且精度有所提升,MAE、MAPE和RMSE分别降低至674.93 MW、7.29%以及816.57%。在第二类模型中,由于增加了气象输入,使得模型预测更准确,选取同样的LSTM算法预测结果对比分析可发现,增加了气象数据的LSTM_2的MAPE较LSTM_1进一步降低了1.50%,这说明了在短期负荷预测中考虑气象因素的必要性。除此之外,在第二类模型中,CNN-LSTM神经网络的预测精度最高,并且预测结果很稳定,模型的MAPE仅为5.31%,相比于CNN以及LSTM_2模型分别提升了15.18%以及8.29%。综上所述,实验发现气象因素引入有利于提高短期负荷预测的精度,并证明了本文CNN-LSTM模型可以有效提取负荷及气象数据的深度特征,预测精度更高。

3.3.2 降维后负荷预测实验及分析

进一步通过实验,验证使用SKPCA对高维气象数据进行降维的优越性。本文又进行了3组对比实验,分别是对高维气象数据采用PCA、KPCA和SKPCA降维,预测算法都选用本文提出的混合深度学习神经网络算法,并同时与上一节未降维的CNN-LSTM预测结果对比。实验中,PCA降维保留4个主成分,KPCA和SKPCA降维保留2个主成分。四种预测模型的预测结果误差分析如表5所示。四种负荷预测结果和预测误差分析结果如图6和图7所示。

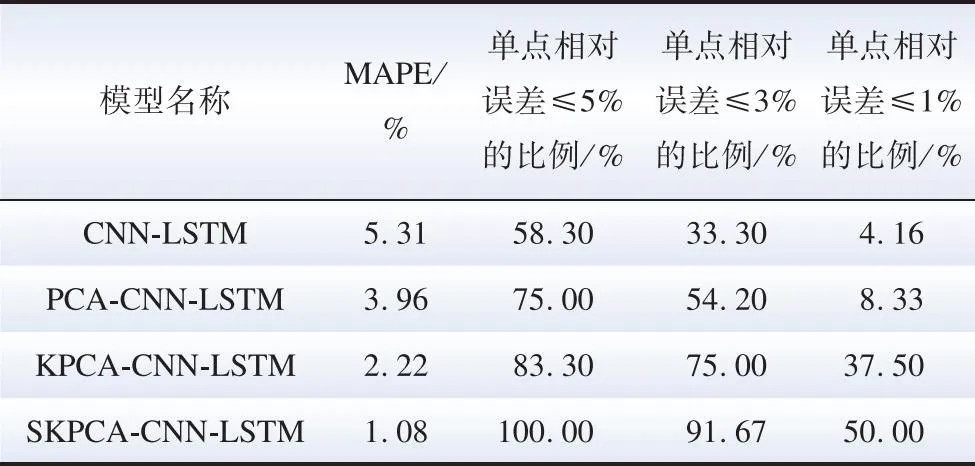
表5 不同预测模型的误差对比Table 5 Error comparison of different prediction models

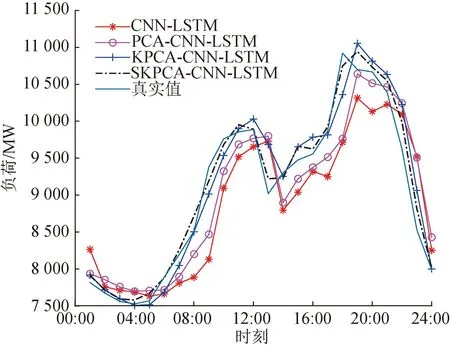
图6 不同降维算法结合CNN-LSTM的负荷预测结果Fig.6 Load forecasting result of different dimensionality reduction algorithms combined with CNN-LSTM

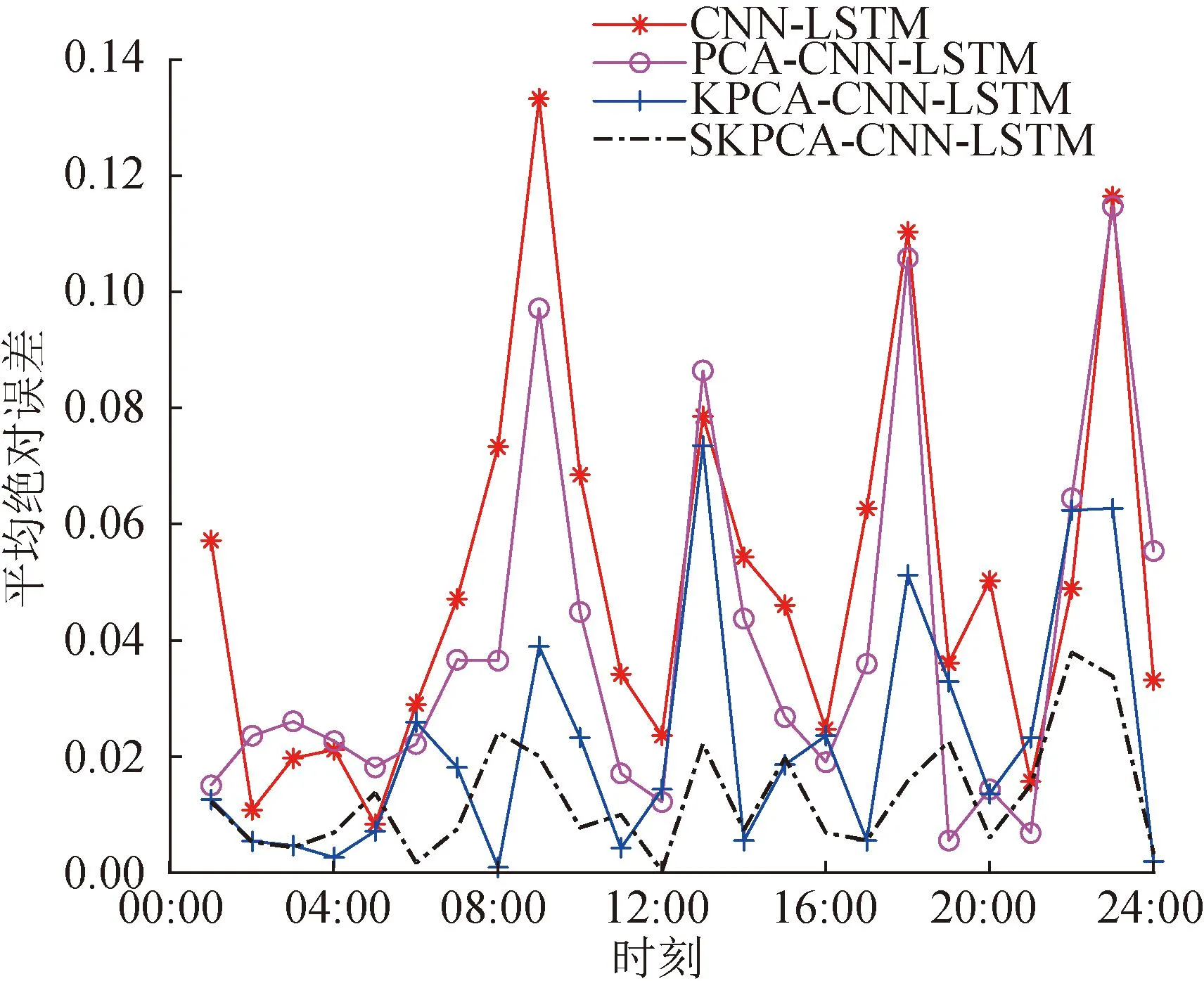
图7 不同降维算法结合CNN-LSTM的误差结果Fig.7 Error result of different dimensionality reduction algorithms combined with CNN-LSTM

由实验结果可知,气象因素直接输入建立的CNN-LSTM模型的MAPE为5.31%,而对气象高维数据进行PCA降维处理后模型的MAPE降低至3.96%,说明气象数据之间具有强相关性,降维处理后预测精度得到了显著提高。经过KPCA、SKPCA数据处理后预测结果的MAPE进一步降低到了2.22%和1.08%。此外,SKPCA-CNN-LSTM的单点误差也低于其余对比模型,单点绝对误差低于1%的预测点占据总预测点的50%,而CNN-LSTM、PCA-CNN-LSTM以及KPCA-CNN-LSTM分别只有4.16%、8.33%以及37.5%。综上所述,SKPCA的降维效果更好,可以降低深度学习模型发生过拟合的风险,从而提高预测精度。

4 结 论

准确的短期电力负荷预测为新型电力系统的调度和供电计划提供可靠的科学依据,通过预知用电行为可以指导电网优化运行,以及引导电力市场及碳市场的运营。本文在现有负荷预测算法的基础上,增加影响负荷的气象数据,提出了基于稀疏核主成分分析(SKPCA)和混合深度神经网络的短期电力负荷预测新方法。本文的结论如下:

1)利用SKPCA降维气象数据,避免高维数据引发深度学习预测模型发生过拟合的风险。相比于PCA和KPCA降维方法,SKPCA降维方法在将7维气象数据压缩至2维的同时,也将平均绝对百分比误差分别降低了72.73%以及51.35%,这表明通过SKPCA降维后气象数据显著提升区域型电力短期负荷预测精度。

2)以降维后的气象数据及历史负荷功率时序数据为输入,构建了基于CNN-LSTM的混合深度神经网络负荷预测模型。通过CNN卷积操作来提取负荷功率及气象数据的空间相关特征,以及LSTM相互连接的隐含层结构和门结构来提取负荷功率数据的时间相关特征,从而全面利用数据的时-空相关性特征,提升负荷功率的短期预测精度。实验表明,相比于CNN和LSTM预测模型,CNN-LSTM模型的平均绝对误差分别降低了16.07%以及11.14%,验证了本文混合深度网络的优越性。

3)最后,本文选用负荷预测公开数据集,对所提算法进行了实验验证。最终,本文方法(SKPCA-CNN-LSTM)的预测精度达到了98.92%,并且保证了所有预测点的单点绝对误差低于5%。本文研究为人工智能模型在区域型短期电力负荷预测中的应用提供了一种新思路。

未来还会开展一些有趣的工作,比如通过遗传算法等启发式算法进行CNN-LSTM模型的超参数优化以及引入额外的电力负荷数据集来验证方法的有效性。