人工智能技术下软件可靠性自动测试系统的设计研究*

魏化永

(安徽交通职业技术学院 安徽合肥 230051)

随着信息社会的进程不断推进，软件技术也不断发展和成熟。如何进行软件质量的检验，保证软件运行稳定可靠，成为业内研究的重点。粒子群算法(particle swarm optimization，PSO)以模拟简化社会模型为基础依据，忽略成员的体积与质量，对粒子成员的加速及速度状态进行研究。粒子群算法的应用越来越广泛，刘道文[1]验证了粒子群算法在提高搜索结果精度的有效性和在解决实际问题上的可行性；文献[2-5]在不同领域应用粒子群算法用以求解优化问题。文章提出基于PSO算法进行改进，并用于软件测试，与GA、PSO算法相比，更具便捷性、高效性。

1研究方法

1.1 PSO算法

PSO算法属于智能优化算法的一种，主要依据人工生命以及演化的计算理论，通过信息共享以及协作以得到问题的最优解。设第一个粒子为aj={aj1…aj2…ajm}，其速度表示为vj={vj1…vj2…vjm}，种群当中最大值表示为nj={nj1…nj2…njm}，同时在该种群中，全局极值表示为vq={vq1…vq2…vqm}。以当前最佳粒子为基本依据，粒子a的位置以及速度的改变如公式(1)及(2)：

(1)

(2)

其中，由于在进行问题优化时通常采用全局搜索的策略，因此惯性权重需要依据迭代进行不断地线性调整。权重调整如公式(3)。

(3)

公式(3)中，ωmax表示最大惯性权重，ωmin表示最小惯性权重，itermax表示迭代的最大次数，iter表示目前的迭代次数。

1.2 GA算法与PSO算法的比较

GA算法主要以自然界的生物进化机制作为启发，演变为计算机算法。GA算法的终止条件有两个，一是最优解已经求得，二是在算法当中，已经预定义好对应的终止条件。

PSO算法主要是以群体优化算法为依据的，模拟的是鸟类的觅食以及飞行等行为，通过个体之间的互相配合完成既定目标，使结果最优。设定目标搜索空间维度为l，一个种群由c个粒子形成，那么l维的第j个粒子则为ajl，飞行速度为vjl，当前粒子搜索过程中，其最优位置表示为njl，在整个粒子组当中，其最优位置表示为nql。各粒子的位置变换由下式决定。

(4)

(5)

上式中，加速常数用正数h1和h2表示，k1和k2为分布在[0，1]当中的任意随机数，s表示对应的惯性因子，当s比较小时，通常用于求解空间小范围内的搜索，当s比较大时，在相对大的范围内搜索更加适用。维度位置上，其变化范围是l(1≤l≤L)，kd维区间为[almin，almax]，速度对应的变化区间为[vlmin，vlmax]，当迭代的速度或者位置超出边界值时，取对应的边界值。

同时由于对加速常数进行了约束并需要判定相应的粒子密度，因此在粒子分支路径中引入相应的路径谓语和路径嵌套。路径谓语的权重系数表示为公式(6)：

(6)

公式(6)中，dj表示迭代至第j代时的加速常数。

路径嵌套的权重系数表示为公式(7)：

(7)

公式(7)中，pj表示第j个粒子路径当前的深度，pmin表示该粒子路径中的最小深度，pmax表示该粒子路径中的最大深度。

由路径谓语以及路径嵌套可以推导出粒子群算法对应的适应度函数，如公式(8)。

(8)

PSO算法的终止条件有两个，一是在粒子群搜索的过程当中，达到其最优位置对应最小的自适应的阈值，二是达到了最优问题搜索迭代次数的最大值。

在以上算法当中，最优位置的最优解通常对应的是整个粒子群，因此该算法也称作全局粒子群优化算法，同时当最优位置的求解只对应某部分粒子群时，被称为局部粒子群优化算法。二者相比，局部粒子群优化算法相对不容易产生局部最优的问题，但是其收敛速度相比全局优化更慢；全局粒子群优化算法具有更快的优化速度，但是容易产生局部最优的问题。

1.3基于PSO算法的软件自动化测试方法

文章在PSO算法的基础上，对算法做出改进。公式(2)中，h1和h2作为粒子对应的加速常数，表示在粒子群当中各粒子交互与传递信息的能力。加速常数在人为取值时，无法精确的符合粒子群在运行过程中的实际情况。针对这一情况，对h1和h2这两个加速常数进行约束，如公式(9)和公式(10)。

(9)

(10)

在进行加速常数的约束之后，可以使PSO算法获得更强的执行度，但过早收敛的问题仍然有几率发生。当出现粒子聚类(即：多个粒子执行适应度函数时得到十分接近的结果)时，此时算法同时判定结果‘最佳’，那么就容易出现过早收敛的情况。因此，通过对粒子密度做出判断的方式，分辨粒子群是过早收敛还是确实达到收敛界限。设第j个粒子的适应度函数为Sj，当粒子群迭代到当前次数时，平均适应度可以通过公式(11)求解。

(11)

其中，总的迭代次数为N，由求得的平均适应度，可以对判定粒子密度的函数进行推导，如公式(12)：

(12)

粒子密度的判定函数在每次迭代完成后执行，并对ρ值进行判定，当ρ值过小时，粒子群算法容易出现过早收敛的情况，算法进行下一次迭代，不进行收敛。

软件自动化测试方法将测试用例中的元素表达为向量a的元素，首先生成测试数据，然后通过软件自动化测试算法对测试数据的最优解进行搜索，并使自适应值最大。

2测试结果分析

2.1测试用例

求解问题质量的好坏与否，通过适应度函数进行判别。因此，适应度函数需要具有结合实际问题的合理结构。对于适应度的评估，需要依靠程序路径对应的分支谓词，既需要考虑到分支谓词对应的特性，同时需要使用到程序插桩。

程序插桩以及分支函数，可以通过以下示例进行说明。下列为等边三角形的判别函数，通过C语言进行实现。

voidEquTri (int a，int b，int c)

{if(((a+b+c)&&((b+c)>a)&&((a+c)>b))

if((a>0&&a<100)&&(b>0&&b<100)&&(c>0&&c<100))

if((a==b)&&(b==c))

printf(“等边三角形”)

else

printf(“不是等边三角形”)

2.2实验结果分析

通过实验，对GA算法以及改进PSO算法在进行等边三角形对应的判断函数进行最优解的求解过程进行对比。表1中，对GA算法以及PSO算法当粒子种群或者粒子数在100～280区间内时，其迭代时间以及迭代次数的最优解做出表征。

表1 使用改进粒子群算法与遗传算法生成等边三角形实验数据的迭代时间和次数

同时，在多次实验的过程中，对可能出现路径覆盖率进行统计分析，在覆盖率比较中，结合传统粒子群算法进行对比，结果如图1所示。

图1 不同算法路径覆盖率比较

图1中，结合粒子群算法或者遗传算法的测试方式所得结果较接近，其路径覆盖率处于40～50%左右，改进的粒子群算法能够保证路径覆盖率达到80%左右。也就是说，改进的粒子群算法对可能出现的路径覆盖率更高，在软件测试的过程中，更加可靠和全面。

算法的迭代次数表明了算法是否高效，结合传统粒子群算法对不同算法的迭代次数进行比较，结果如图2所示。

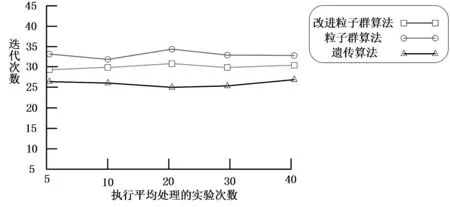
图2 不同算法的迭代次数比较

图2中，遗传算法在达到收敛时所需要的迭代次数平均在27次左右，传统粒子群算法在达到收敛时所需要的平均迭代次数在32次左右，改进粒子群算法在达到收敛时所需要的平均迭代次数在30次左右。三种算法达到收敛时需要的迭代次数相对接近。结合图1和图2，改进粒子群算法在收敛速度与其他两种算法大致相同的情况下，具有更好的路径覆盖率，能够更为精确和全面的进行软件测试。

在软件测试的自动化运行以及可靠性运行上，只有保证测试算法有效、准确，才能够保证软件质量更为可靠，同时保证测试数据分析合理快速。生成更为精确明了的测试数据，是软件测试最有效的保障。基于PSO算法改进的软件自动测试方法，与GA算法相比，更加简洁高效，同时在系统设置当中，对参数进行了进一步的优化，使得参数调整更少，更加易于实现。

3结论

以人工智能技术为前提，以PSO算法为基础依据改进后的智能算法，能够在软件测试，数据生成的过程当中，起到更为高效和精确的效果。实验结果表明，该方法切实可行，在软件可靠性自动测试的过程中更为适合。