基坑开挖对下卧盾构隧道土层变形的影响研究*

2024-01-03鲁芬婷陈倩倩

九江学院学报(自然科学版) 2023年4期

鲁芬婷陈倩倩

(皖江工学院土木工程学院安徽马鞍山 243000)

基坑开挖工程随着基建发展的加快而被广泛采用，但同时基坑工程也面临这日益复杂的施工环境，在实际施工的过程当中，基坑开挖由于各种因素会对盾构隧道造成印象，导致其出现一定的变形。如何对这种变形影响做出更加全面和精确的计算，成为基坑开挖工程当中十分重要的施工筹备工作。

1力学模型的建立及计算

1.1力学模型的建立

隧道下卧基坑为矩形，考虑到仿真以及数值模拟过程当中，建模较为复杂，计算耗时较长，因此通过对地基模型上添加弹簧层以模拟覆土层对隧道的影响，并对隧道变形相应的公式做出一定的简化。具体上，对基坑的卸荷应力进行求解时，暂不考虑基坑开挖时降水的影响以及时空影响，对土体弹塑性进行分析；在进行附应加力的求解时，忽略既有隧道对基坑卸荷时的影响，假设土体表现为均质、半弹性，空间体为半无限状态，其力学模型建立如图1。

(1)平面图

1.2力学模型的计算

1.2.1坑底卸荷的计算基坑开挖过程中，由于采用弹塑性材料作为土体，应增加对残余应力的分析。首先确定相应的残余应力系数β，如公式(1)所示：

(1)

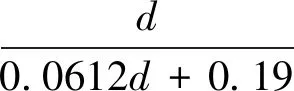
坑底对应的卸荷的荷载按下式计算：

δ=(1+β)ωd#

(2)

(3)

(4)

式(3)及式(4)中，坑底对应的积分区域用Ω表示，坑底某点(x2，y2，d)及地面的对称点(x2，y2，-d)与给定隧道轴线点的距离用R1、R2表示，计算如公式(5)及公式(6)。

(5)

(6)

1.2.2坑壁卸荷的计算由于坑壁的围护结构对侧向应力会产生一定的影响，因此在进行坑壁卸荷分析时，首先应考虑静止土压力与主动土压力的关系，也既相应的折减系数α，即公式(7)。

(7)

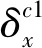
z2dy2dz2

(8)

(9)

公式(8)及公式(9)中，①号侧壁的积分用ΓC1表示，静止土压力系数用K0表示，通常该系数由实际实验求取。如果暂无法进行实际实验，土质为粘性土时可取0.95-sinθ'，为砂性土时可取1-sinθ'，其中θ'表示内摩擦角，坑底某点(x2，y2，z2)及地面的对称点(x2，y2，-z2)与给定隧道轴线点的距离用T1、T2表示，计算如公式(10)及公式(11)。

(10)

(11)

(12)

(13)

2隧道的纵向变形

2.1纵向变形的计算模型

隧道纵向变形的模型建立需要考虑两个方面的影响，一是隧道中上覆土层的影响，二是隧道中下部弹簧的影响。综合考虑进行地基梁模型的简化，如图3。

图3 地基梁简化模型

图3中，盾构隧道的y-ω坐标系中，dy为某一段微元段，对该微元段所作的受力分析如图4。

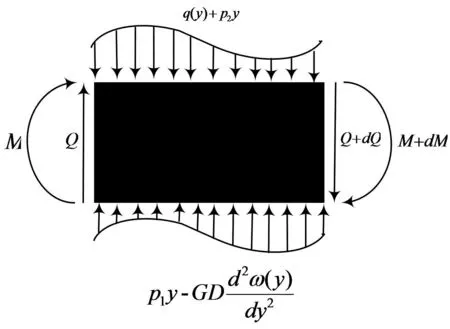
图4 微元段受力分析

(14)

公式(14)中，材料对应界面惯性矩用I表示，弹性模量用E表示，等效的纵向抗弯刚度用EI表示，剪切模量用G表示，附加荷载用q(y)表示，可以通过公式(12)及公式(13)求取，位移用ω(y)表示。在地基梁模型假设中，某点变形S与应力P呈正相关，则：

(15)

公式(15)中，K1、K2分别表示地基上下部对应的基床系数。如果上下部的地基土质相近，可以用同一值K表示。

2.2计算模型的求解

对挠度的微分方程通过有限差分法进行估算，将隧道离散为长度为c的i+4个独立的单元，并在隧道左侧补充-2、-1两个虚拟单元，右侧补充i+1、i+2两个虚拟单元，其离散分析的示意图如图5。

图5 离散分析示意图

图5中，隧道两端自由，分段位移用ω0，ω1，…ωi表示，那么对应的弯矩以及剪力可以通过公式(16)求得。

(16)

由上推导出个分段的位移公式，表示为公式(17)。

(K+2KS-Gs)ω=Qt#

(17)

公式(17)中，地基以及隧道的刚度矩阵用KS及K表示，截切层的刚度矩阵用Gs表示，隧道位移列的向量用ω表示，附加荷载列的向量用Qt表示。可以推导出隧道的附加剪力以及附加弯矩，表示如公式(18)。

(18)

3实证分析

以我国某城市某建筑为例，其基本参数如下：基坑规格为，L×B=30m×20m，开挖深度d的数值为7m，围护结构的规格为深15m，厚8m，同时盾构隧道纵轴与围护结构水平方向的最小净距s的数值是4m，抗弯刚度的数值721×107kN·m2，管片外径的数值6m，厚35m，在使用改进模型的方法计算时，折减系数设置为25%。对隧道拱顶部位的变形情况做出分析，通过Winkler地基梁模型、改进模型以及实测数据的对比，所得结果图6和图7所示。