基于GNSS的多基地雷达目标定位与运动参数提取精度分析

黄 攀,叶新红,陈 静,杭余晖,袁 康

(国家电投江苏海上风电公司,江苏 盐城 100001)

0 引 言

基于全球导航卫星系统(Global Navigation Satellite System,GNSS)的外辐射源雷达系统具有良好的“四抗”性能。利用GNSS信号进行目标探测,不仅可以扩展可用辐射源的种类,而且对于弥补当前主动雷达的不足具有重要意义。相比于其他辐射源,GNSS卫星具有全球覆盖性,地球上任何一个点在任意时刻有16～32颗卫星同时照射。因此,基于GNSS的外辐射源雷达具备潜在的多基地雷达特性。

2018年,英国伯明翰大学Ma H[1]等人研究了一种基于GNSS的PBR动目标显示方法,利用Galileo卫星导航系统实现了对海上目标的检测。同年,作者[2]利用多个卫星得到了目标的位置信息。2021年,武汉大学陕娟[3]、李焱[4]等人利用北斗同步卫星实现了对江面目标的探测,证明了利用北斗同步卫星探测目标的可行性,同时还研究了长时间积累下目标的跨分辨单元走动补偿问题。

在检测到目标后,可利用基于GNSS的外辐射源雷达多基地特性实现目标定位和运动参数提取。本文分析了基于GNSS的多基地雷达目标定位与运动参数提取精度,并利用克拉美-罗下界(Cramer-Rao Lower Bound,CRLB)研究目标定位和运动参数估计精度随卫星数量和目标回波能量之间的关系。

1 目标定位与运动参数提取方法

基于GNSS的多基地外辐射源雷达系统结构如图1所示,O-XYZ为本地参考系,假设系统中共有M颗卫星、1个接收机。

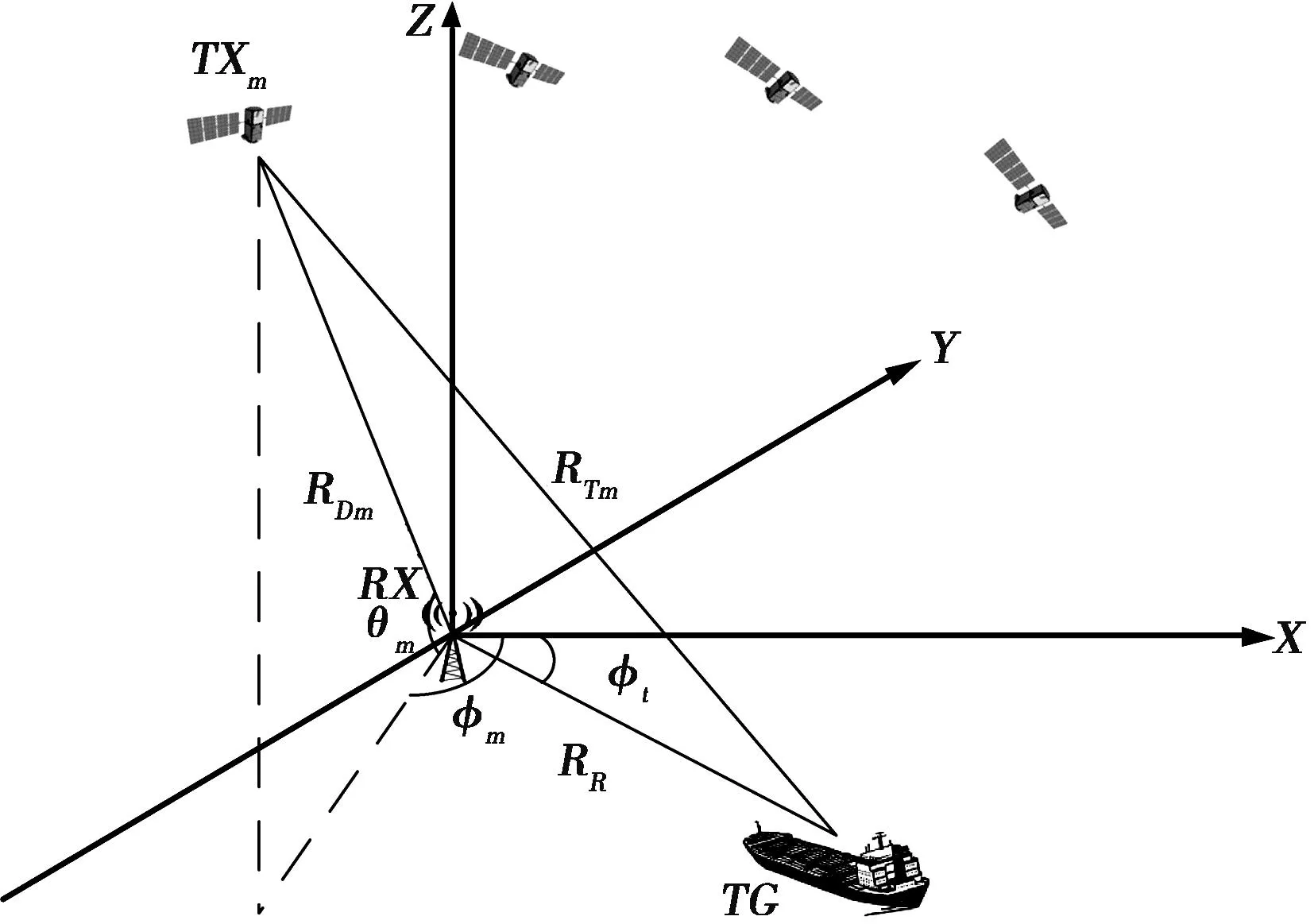
图1 基于GNSS的多基地雷达系统几何结构

为不失一般性,假设接收机位于系统坐标原点,接收机的坐标可表示为RX=r=(0,0,0)T,目标和第m颗卫星的坐标分别为

TG=xt=(xt,yt,zt)T

(1)

TXm=xi=(xm,ym,zm)T

(2)

卫星到接收机、卫星到目标、目标到接收机的距离分别为

(3)

RTm=‖xt-xi‖

(4)

(5)

则第m颗卫星对应的双基地距离可表示为

Rm=RTm+RR-RDm

(6)

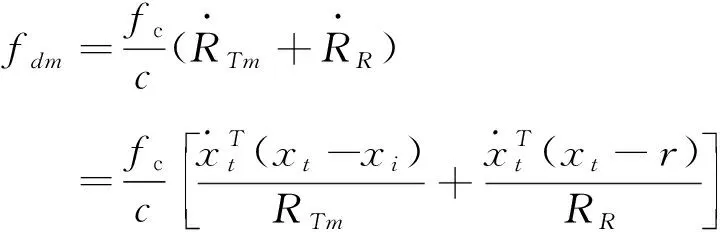
(7)

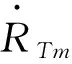
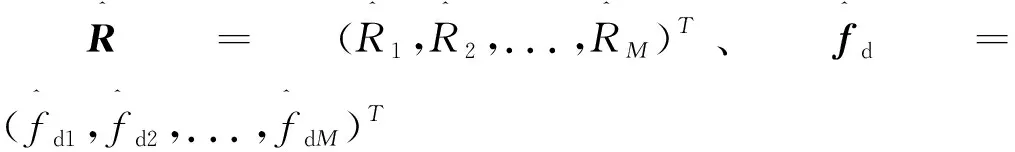
(8)

对式(8)两边平方,得到

(9)

对式(9)沿时间求导,有

(10)

将式(9)和式(10)合并为矩阵形式:

AX=B

(11)

其中:X为与目标位置和运动信息有关的参数矩阵;B为常数向量;且

(12)

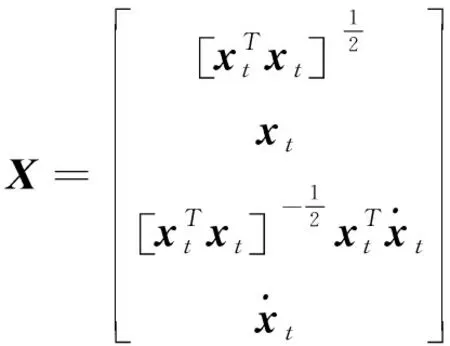
(13)

(14)

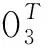
将长时间积累算法处理获得的双基地距离和多普勒信息代入矩阵A和B,并求解式(11),即可得到目标的位置和速度信息。

式(11)的最小二乘解可表示为

X=(ATA)-1ATB

(15)

2 精度分析

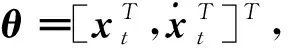
(16)

其中:α0为测量向量的真实值;Q为测量向量的协方差矩阵,且

Q=diag(ΖM×M,ΩM×M)

(17)

其中:ΖM×M、ΩM×M分别为双基地距离和多普勒的协方差矩阵,可分别表示为

(18)

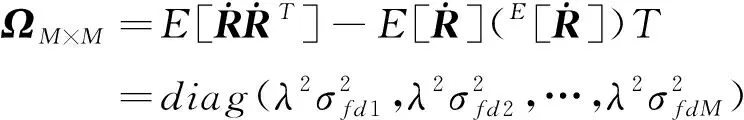
(19)

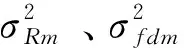
根据文献[5]和[6],双基地距离和多普勒的方差与目标回波的SNR有关,具体计算公式为

营造技艺的“变”实则是探讨建筑本体在“源”、“流”之间的变化关系。如图1所示，一是以营造“圈”为核心，经过不同营造“流”的路径，发展出相应的演变结果；二是营造之“圈”相互交流时部分区域发生的“变化”。这种营造“变”包含了共时性和历时性两个层面。

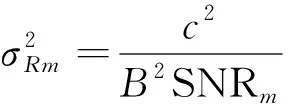
(20)

(21)

其中:B为信号带宽;Tcoh为相参积累时间;SNRm为第m颗卫星信号处理后的目标回波SNR。

由式(16)可得Fisher信息矩阵(Fisher Information Matrix,FIM)为

(22)

其中:∂α/∂θ为关于目标位置和速度参数的偏导数,其子矩阵形式可以表示为

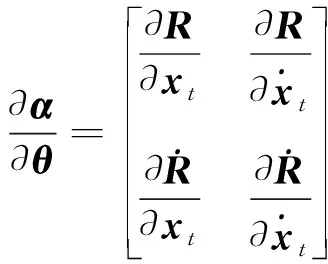
(23)

根据式(6)和式(7)计算∂α/∂θ的值。计算结果分别为

(24)

(25)

(26)

将∂α/∂θ和测量向量的协方差矩阵代入式(22),即可得到FIM。根据定义,FIM的逆为CRLB[7],因此有

CRLB(θ)=FIM(θ)-1

(27)

3 仿真分析

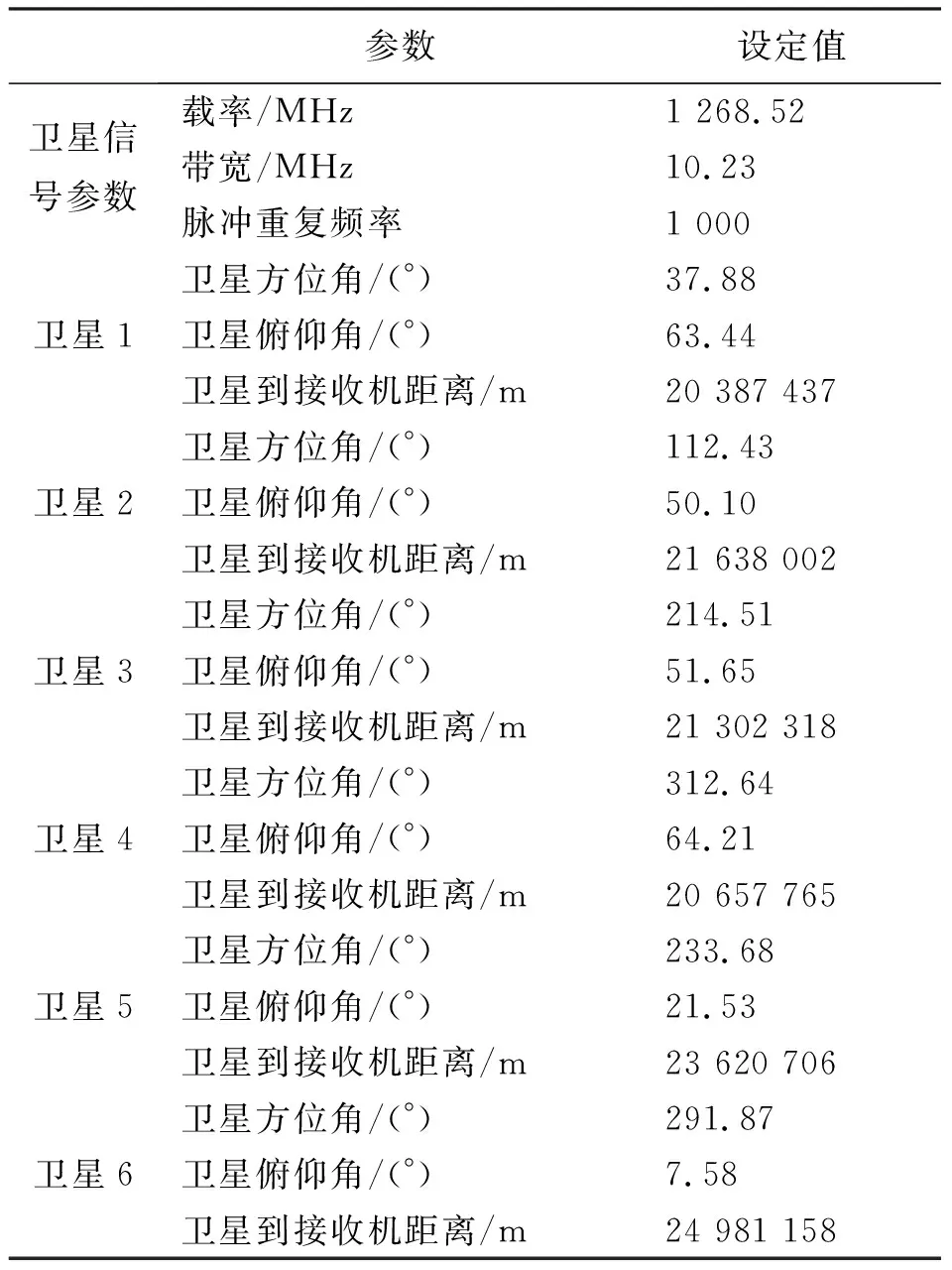
表1 雷达系统仿真参数设置

利用CRLB分析基于GNSS的多基地雷达联合定位和速度估计方法的参数估计性能。由式(20)和式(21)可知,观测矩阵的协方差矩阵与信号处理后的回波SNR及CPI有关。本节设定CPI均为2 s,因此只须考虑目标回波信号处理后的回波SNR。

目标的回波SNR受目标RCS影响,由于每颗卫星的位置不同,照射目标的角度不同,不同卫星照射下目标的RCS也有所不同。设第m颗卫星目标信号处理后对应的SNRm=amSNR,其中系数am满足∑mam=M。分两种情况讨论目标回波SNR与该方法目标定位及速度估计CRLB之间的关系。

(1)各个卫星信号处理后的目标回波SNR相同

首先考虑各个卫星信号处理后的目标回波SNR相同即am=1的情况。为了描述CRLB随SNR的变化关系,本文仿真每颗卫星信号处理后的目标回波SNR变化范围为5 dB～25 dB,以表征目标定位与参数提取方法在不同SNR下的参数估计性能。

分别仿真在4、5、6颗卫星照射下本章算法目标定位和速度估计CRLB,结果如图2所示。其中图2(a)为目标定位结果CRLB,可以看出随着目标回波SNR增加,目标定位精度越来越高;随着卫星颗数增加,目标定位CRLB越来越低,说明辐射源越多,定位精度越高。当目标回波SNR大于20 dB时,不同卫星颗数下目标位置CRLB接近相等。可以推断,当目标回波SNR足够大时,使用较少卫星也能取得良好的定位精度。图2(b)为卫星运动参数估计CRLB。同样,随着SNR越大、辐射源数量越多,目标的速度估计精度越高。

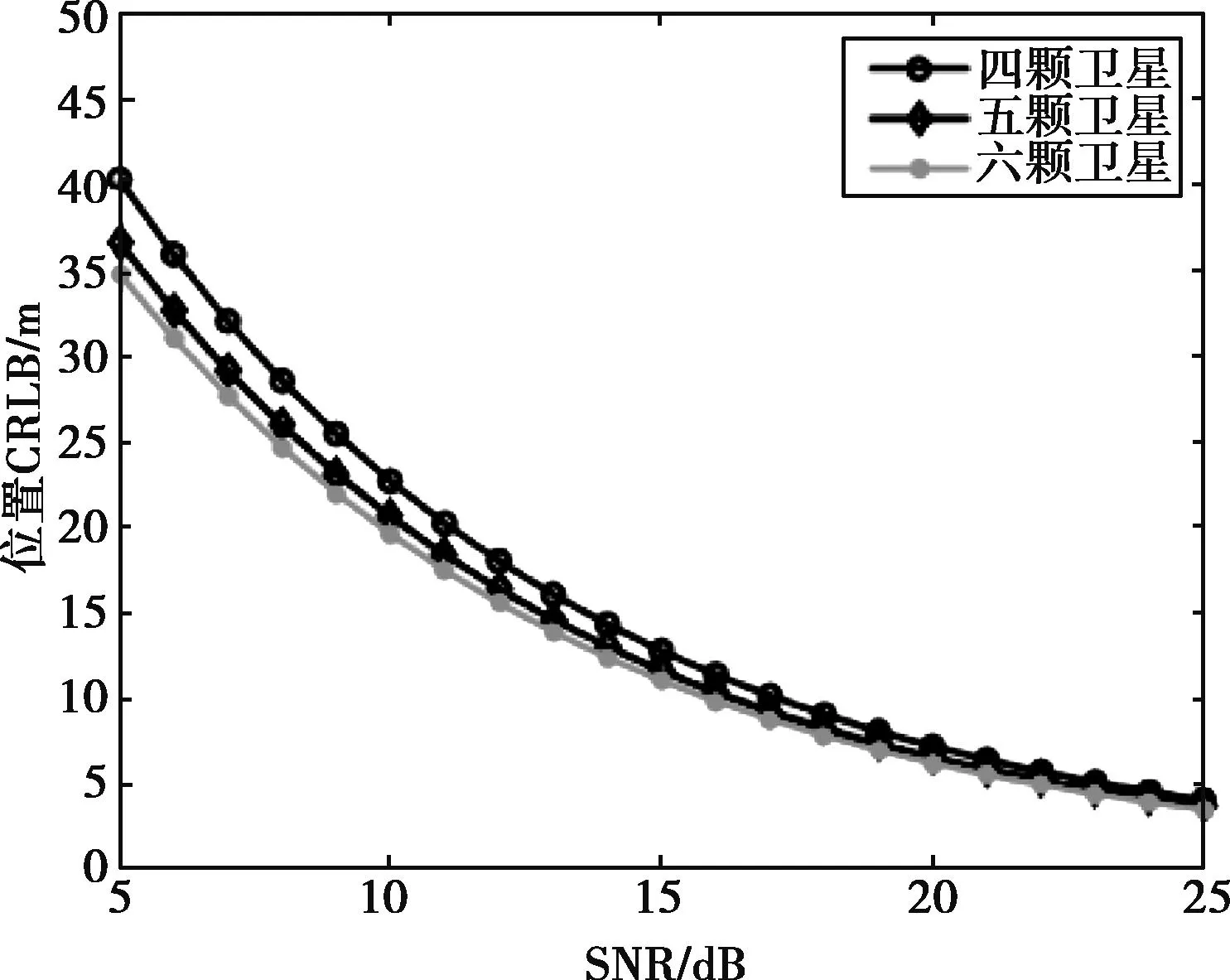
(a)位置CRLB

(2)各辐射源对应的回波SNR不同

当各辐射源对应的回波SNR不同时,仿真在6颗卫星同时照射下,不同回波SNR对定位和速度估计精度的影响。3组目标回波SNR系数am分别设置为a1,2,3,4,5,6=1;a1=2,a2,3=0.5,a4,5,6=1;a1=4,a2=1,a3,4,5,6=0.25,仿真结果如图3所示。可以看出:当不同卫星照射下目标回波SNR不同时,目标定位精度和速度估计值均比各个卫星SNR相等时低;对比参数二和参数三仿真结果,各个卫星之间SNR相差越大,目标定位和速度估计值的精度越低。

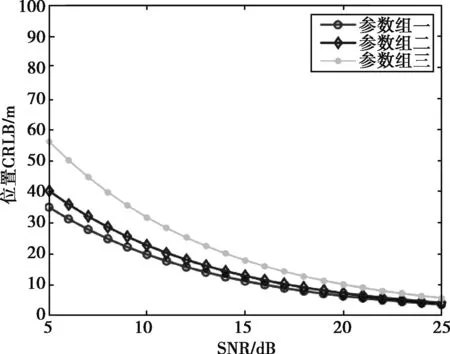
4 结束语

基于GNSS的外辐射源雷达具备潜在的多基地特性,本文利用仿真实验数据分析了基于GNSS的多基地雷达系统目标定位和运动参数提取精度。仿真结果表明,基于GNSS的多基地雷达系统目标定位与运动参数提取精度随卫星颗数变化,卫星颗数越多,目标定位和运动参数提取精度越高。同时,不同卫星照射目标的角度不同,导致目标的回波SNR有所差异。在卫星颗数相同时,不同卫星照射下目标的回波SNR相差越小,目标定位和运动参数提取的精度越高。