基于全局划分与局部划分的自适应活动轮廓模型
2024-01-03熊点华张守成唐利明严俊潇
熊点华,张守成,唐利明,方 壮,严俊潇
(1.广西民族师范学院 数理与电子信息工程学院,广西 崇左 532200;2.湖北民族大学 数学与统计学院,湖北 恩施 445000;3.塔里木大学 信息工程学院,新疆 阿拉尔 843300)
0 引言
为了对图像进行更好的分析和理解,需要把图像分成几个区域,这是图像分割的主要任务.近年来随着人工智能的发展,基于深度学习的图像分割方法[1-4]相继提出.基于深度学习的图像分割的方法效率高,但需要大量的实验样本进行训练,因此相关理论的可解释性还有待完善.传统的图像分割方法主要有聚类分析、阈值分割、活动轮廓 (Active Contour Method,ACM)等,其中基于ACM的变分水平集[5-6]具有良好的实验效果和完备的数学理论,受到研究者的关注,并在人脸识别[7-8]、卫星定位[9]等领域得到了广泛应用.
活动轮廓模型分为全局活动轮廓和局部活动轮廓.经典的全局活动轮廓模型是Chan和Vese[10]提出的Active contour without edge model模型,又称CV模型,其分割结果不受梯度影响,但对灰度不均图像的分割结果较差.Li等[11]提出局部二值拟合能量(Local binary fitting energy,LBF)模型.LBF模型中的局部能量项可以很好地捕捉图像的局部信息,但它对初始轮廓线位置和图像中的噪声敏感.全局和局部活动轮廓模型各有优点,Wang等[12]结合CV模型与LBF模型的优点,提出了由局部和全局强度拟合能量驱动的活动轮廓(local and global intensity fitting,LGIF)模型.LGIF模型能分割灰度不均图像,但不同的初始轮廓所对应的权重系数不同.Han等[13]建立了基于迭代次数的自适应权重函数,提出基于Jeffreys 散度的活动轮廓(Active contour model on Jeffreys divergence,JD-ACM)模型,JD-ACM模型对权重系数和初始轮廓鲁棒,但未考虑图像的形状、纹理等特征.
在全局和局部活动轮廓的框架下,研究者基于不同的理论建立了诸多活动轮廓,并得到了良好的实验效果.Min等[14]结合图像的纹理特征,提出了基于强度-纹理模型的图像分割水平集方法(An Intensity-Texture model based level set method,ITLSM)模型,将目标和背景内部区域分为灰度值比平均灰度值大和比平均灰度值小的两个部分,用于分割复杂两相图像.该模型对模糊边界的拟合能力较差.Ding等[15]在用局部计算图像的平均灰度定义两个预拟函数,提出了局部拟合能量驱动的活动轮廓快速图像分割(Active contours driven by local pre-fitting energy,ACM_LPF)模型,缩短了基于图像拟合活动轮廓模型分割图像的时间.ACM_LPF模型只适用于两相图像的分割.Zhang等[16]基于图像恢复(Total Variation[17],TV)模型,引入多尺度项,提出了用于多尺度图像分割的图像分割(A Variational level set model for Multi-scale,MCV)模型,增大尺度参数,可将噪声、纹理去掉,但边界提取项为CV模型中的能量项,不适用于多相图.上述活动轮廓模型虽然能分割灰度不均图像,但对边界模糊图像的分割结果较差.Fang等[18]构建区域能量,加入边缘能量对水平集函数进行正则化,提出了基于混合和局部模糊区域能量驱动的边缘区域活动轮廓(Hybrid and local fuzzy region-based energy,HLFRA)模型,HLFRA模型可分割高噪声、高灰度不均图像,但对低对比度图像的边界拟合能力较弱.Fang等[19]提出基于模糊区域的由全局和局部拟合能量驱动活动轮廓 (Fuzzy region-based by global and local fitting energy,GLFIF)模型,GLFIF模型能快速分割边界模糊图像,但会提取到图像中一些非必要的细节.
为了分割边界模糊的图像以及遥感图像,文中提出了基于全局划分与局部划分的活动轮廓模型.DGDL模型中的全局划分能量项用于捕捉图像的整体目标,局部划分能量项用于捕捉图像灰度的局部变化,自适应函数自动调节全局与局部能量项的比重.DGDL模型用自适应函数对全局能量与局部能量进行自动选择,并且DGDL模型的分割结果不受初始轮廓位置影响.此外,模型中的全局划分能量项可以很好地捕捉图像的整体目标,局部划分能量项可以捕捉图像灰度的局部变化,采用自适应函数自动调节全局与局部能量项的比重.
1 背景回顾
1.1 LGIF模型
在LGIF模型[12]中,考虑局部与全局强度信息, CV模型和LBF模型中能量项中的能量项分别作为全局和局部能量,将二者线性组合.LGIF模型中的能量泛函定义如下:
ELGIF=(1-w)ELIF(f1,f2,φ)+wEGIF(c1,c1,φ)+ER(φ)
(1)
式(1)中,w∈(0,1)为权重系数.
ELIF为局部能量项,定义如下:
(2)
其中I(y)是图像,Kσ(x-y)为高斯窗口,f1(x)和f2(x)是LBF模型中局部目标和背景内的灰度均值,φ作为水平集函数.H(·)是Heaviside函数[10], Dirac函数是H(·)的光滑导数,分别定义如下:
EGIF为全局能量项,定义如下:
(3)
其中,c1和c2分别是CV模型中目标和背景内的灰度均值.
为了精确计算水平集函数及演化,我们需要对水平集函数进行正则化,惩罚偏离带符号的距离函数,定义如下:
(4)
这里μ和υ是大于0的常数.
采用梯度下降法[20-21],构建欧拉-拉格朗日方程[22],求解式(1)得c1、c2和f1(x)、f2(x)的极小值:
(5)
(6)
另外,得出水平集的演化公式:
(7)
在式(8)中,F1与F2的定义分别如下:
F1=w[-λ21|I(x)-c1|2+λ22|I(x)-c2|2]
(8)
(9)
LGIF模型对初始轮廓鲁棒,能分割灰度不均图像,但很难将不同的权重系数与图像信息进行关联,权重系数受初始轮廓位置的影响,限制了LGIF模型的应用.
1.2 ITLSM模型
在ITLSM模型中,通过引入划分函数,将每个区域划分为两个部分:一个区域灰度值比平均灰度值大,一个区域灰度值比平均灰度值小.划分函数定义如下:
(10)
分别用CV模型中的c1和c2作为目标与背景的灰度均值,定义如下:
(11)
ITLSM模型中的能量项定义为:
(12)
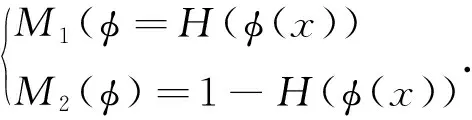
(13)
(14)
全局划分能量项用于拟合复杂图像的整体目标轮廓,并降低了模糊边界对图像分割结果带来的影响,此外,还保持了初始轮廓在演化过程中的鲁棒性.但ITLSM模型易受图像灰度的影响,ITLSM对灰度值较大区域的拟合能力较差.在本文模型中,ITLSM模型中的能量泛函被用作全局划分能量项.
2 DGDL模型与算法
为了分割边界模糊图像,降低基于划分函数的活动轮廓模型对图像中低对比度边界的干扰,建立基于全局与局部划分的自适应活动轮廓(DGDL)模型.DGDL模型由三部分组成,分别为全局划分能量项、局部划分能量项、自适应函数和正则项.
2.1 局部划分能量项
为了增强基于划分活动轮廓图像对边界模糊图像边界的提取能力,并捕捉图像的局部灰度变化,我们提出了一个基于局部均值的局部划分函数,定义为:
(15)

(16)
局部划分能量项定义为:
(17)
在式(17)中,DL1(x)=H(I(y)-f1(x)),DL2(x)=H(I(y)-f2(x)),ρ11、ρ12、ρ21、ρ22为常数,b11(x)为局部目标区域内大于局部目标区域均值的划分区域灰度均值,b12(x)为局部目标区域内小于局部目标区域均值的划分区域灰度均值,b21(x)为局部背景区域内大于局部目标区域均值的划分区域灰度均值,b22(x)为局部背景区域内小于局部目标区域均值的划分区域灰度均值.另有:
分别求解关于b11(x),b12(x),b21(x),b22(x)的极小值,得:
(18)
(19)
(20)
(21)
局部划分能量项用于捕捉图像灰度的局部变化,并且能精准捕捉边界模糊图像中的关键目标,对边界模糊图像进行分割,不会造成边界泄露或欠分割.
2.2 DGDL模型
本文将ITLSM模型中的全局划分能量项与局部划分能量线性组合,将自适应函数作为权重系数,加入正则项约束水平集的演化,得到DGDL模型,定义如下:
EDGDL=w(n)EDG+(1-w(n))EDL+ER
(22)

-λ21(I(x)-d21)2+λ22(I(x)-d22)2)-(1-w(n))δ(φ)(ρ11e11-ρ12e12+ρ21e21-ρ22e22)
(23)
上式中,d11、d12、d21、d22为全局划分能量项给出,另有:
采用交替迭代算法实现仿真实验,DGDL模型的主要算法步骤如下:
Step1: 输入图像并设置初始轮廓;
Step2:设置最大迭代次数N,参数μ、υ、w(n);
Step3:通过公式(13)~(14)计算d11、d12、d21、d22;
Step4:由式(18)~(21)计算b11(x)、b12(x)、b21(x)、b22(x);
Step5:通过公式(23)更新水平集函数;
Step6:当n 实验仿真环境为LAPTOP-RETV7IRD Aspire A515-516Intel(R) Core(TM) i5-7200U CPU ⓒ 2.50GHz 2.71 GHz RAM4.0G matlab2014a.对比模型为LGIF、ITLSM、MCV、ACM_LPF、HLFRA和GLFIF模型.其中,LGIF为经典的混合活动轮廓模型, ITLSM模型中含有划分函数,MCV、ACM_LPF、HLFRA和GLFIF模型为近年的活动轮廓模型,其中MCV和GLFIF模型能分割噪声图像,HLFRA和ACM_LPF对边界模糊和灰度不均图像有较好的分割效果.此外,上述活动轮廓模型都对初始轮廓鲁棒,因此,选取各个模型初始轮廓固定为(63∶103,69∶99),各模型的参数均为模型所给出.DGDL模型的参数为μ=0.01×255×255,t=0.1,ε=1.为更好地验证DGDL模型与其他模型的分割能力对比,采用Jaccard系数[23](Jaccard similarity Coefficient,JSC),DSC系数[24](Dice Similarity Coefficient,DSC),体素重叠误差[25](Volumetric overlap error,VOE)对分割结果进行度量. 在图像分割模型中常用多孔扳手图验证模型对活动轮廓模型初始轮廓的鲁棒性(见图1).初始轮廓位于图像中不同的位置(a1~a7)以及对应的结果(b1~b7).在不同初始轮廓条件下,DGDL模型都能很好地把扳手的轮廓拟合出来,且在不同初始轮廓下DGDL模型对扳手图的分割结果一致,对初始轮廓鲁棒提高了实验效率. 图1 DGDL模型在不同初始轮廓下的分割结果 选取多目标且含有低噪声的合成图像,分别验证不同模型分割合成图像所用的时间与分割结果的DSC值.由图2可见,DGDL模型在迭代5次以后就能稳定地提取到不同图像的目标, 各模型在迭代次数为30次以后轮廓的演化趋势较为平稳.而ACM_LPF模型却不能很好地分割低噪图像,但该模型分割结果的DSC值变化不大,说明结果平稳,因此实验中各模型的迭代次数均设置为30.由表1可知,各模型在迭代次数大于20以后分割结果的DSC系数就趋于稳定,但DGDL模型时耗短且DSC系数较高,说明DGDL模型具有较高的分割效率. 表1 各模型在不同迭代次数的耗时与DSC系数对比 (时间(秒)/DSC系数值) 图2 各模型在不同迭代次数下的分割结果 选取含有灰度不均区域的多目标图像(Image A,B,C)和含低噪声(Image D)图像作为分割对象,验证各模型分割合成图像的能力.在图3中,分割Image A时,各模型都能有较好的分割结果,各对比模型的分割结果DSC系数都较高.由于Image B背景区域的灰度分布不均匀,仅有ITLSM和DGDL模型取得较好的分割结果.由表2可知,DGDL模型分割Image B的评价系数优于其他模型.在分割Image C时,DGDL模型中的能量泛函可以很好地提取图像目标,从而取得良好的分割结果.DGDL分割Image C的评价指标优于文中其他对比模型在分割Image D时,ITLSM模型和ACM_LPF模型会产生较大误差,而其他对比模型都能较好地分割噪声图像,说明这两个模型对噪声图像的分割能力较弱.另外,综合表2来看,DGDL模型分割结果的DSC系数、JSC系数和VOE系数都较高. 表2 各模型对合成图像分割结果的指标对比 图3 各模型对合成图像的分割结果对比 选取3幅CT图(Image A,B,C)和1幅皮肤病变图(Image D),验证各对比模型对医学图像的分割能力,第一列为初始轮廓线所在位置.从图4可看出,在分割Image A和Image B时,ACM_LPF和GLFIF模型的分割能力较弱.表3中对分割结果的评价系数也很好地验证了这点.在分割Image C时,由于ITLSM模型对图像灰度较高区域目标的拟合能力较弱,导致ITLSM模型分割Image C时产生了较大失误.在分割皮肤病变Image D时,由于在模型中引入了划分能量项,仅有ITLSM和DGDL模型能较好地分割出Image D中的目标.这两个模型分割Image D时的评价系数明显优于其他对比模型,验证了基于划分函数模型的分割能力.另外,在评价指标的对比上,DGDL分割医学图像时都有良好的结果,说明DGDL模型对医学图像有良好的分割能力. 表3 各模型对医学图像分割结果的评价指标对比 图4 各模型对医学图像的分割结果对比 在Weizmann数据集[26]上进行测试,并选取Weizmann数据集上的图像作为分割对象,分割结果的指标均值如表4.图5展示了三幅图像(Image A,B,C)的分割结果.这三幅图像都具有模糊的边界,同时背景与目标区域灰度分布不均匀.结果显示,仅有ITLSM和DGDL模型能取得良好的分割结果,其他模型易受图像中灰度不均区域和模糊边界的影响.如图像A,背景区域会对分割结果产生干扰,只有ITLSM和DGDL模型能将图像中的目标区域提取出来.图像B,C中目标区域灰度分布不均匀,ITLSM模型会对图像产生过分割.结合表4可知,DGDL模型的指标优于ITLSM模型. 表4 各模型在Weizmann数据集中分割结果的评价指标对比 图5 各模型对自然图像的分割结果对比 本文采用全局划分能量项捕捉图像的整体轮廓,局部划分能量项捕捉边界模糊图像的边界,提出了DGDL模型,引入一个基于迭代次数的自适应函数作为权重系数.自适应函数实现了全局划分能量和局部划分能量的自动选择,保持了DGDL模型对初始轮廓的鲁棒性.分割结果显示,DGDL模型对初始轮廓鲁棒,并且对医学图像和边界模糊图像有良好的分割结果.另外,DGDL模型分割边界模糊图像的DSC、JSC和VOE系数都较优,验证了DGDL模型的分割能力.需要注意的是,由于基于全局划分的能量项对图像的灰度要求较高,导致DGDL模型在分割灰度值较高的图像时,会产生过分割.3 数值模拟实验
3.1 DGDL对初始轮廓的鲁棒性

3.2 DGDL的分割性能
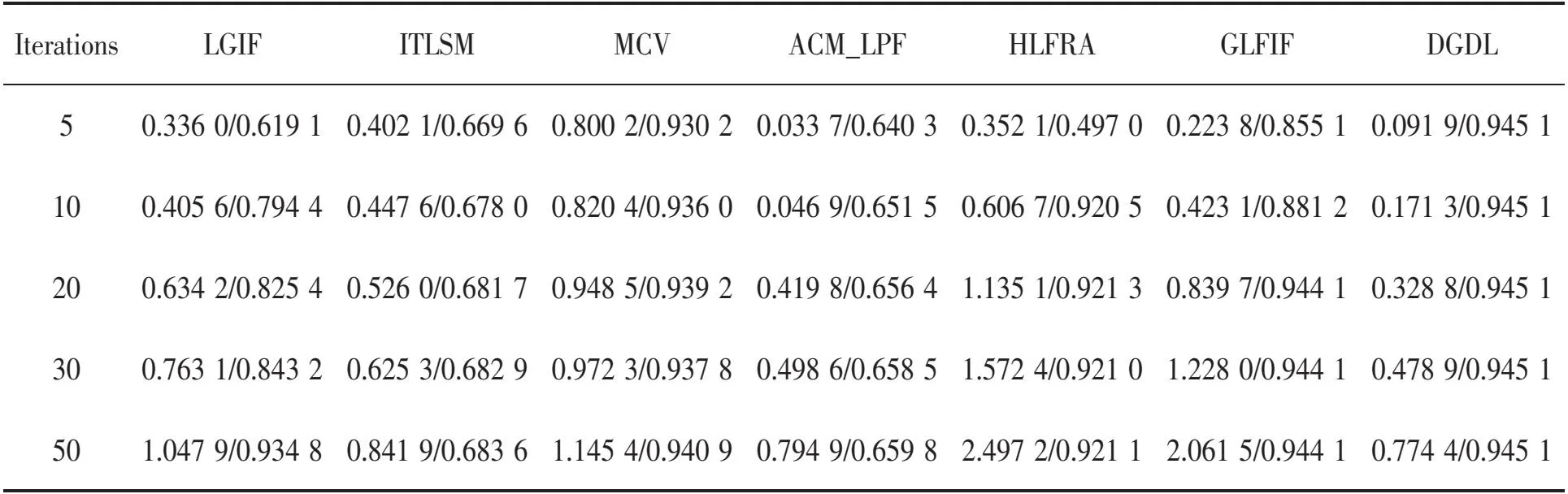

3.3 分割合成图像
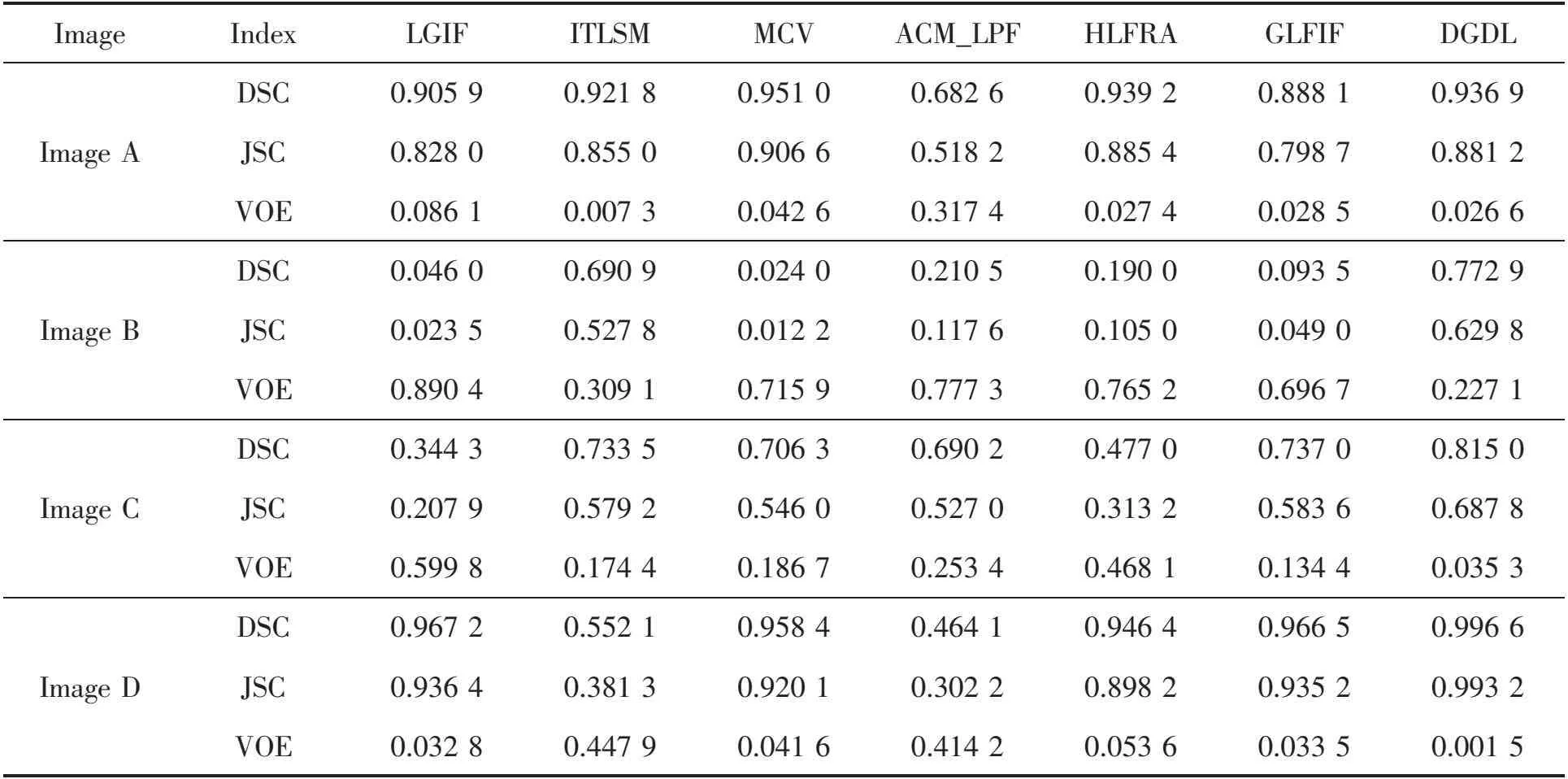

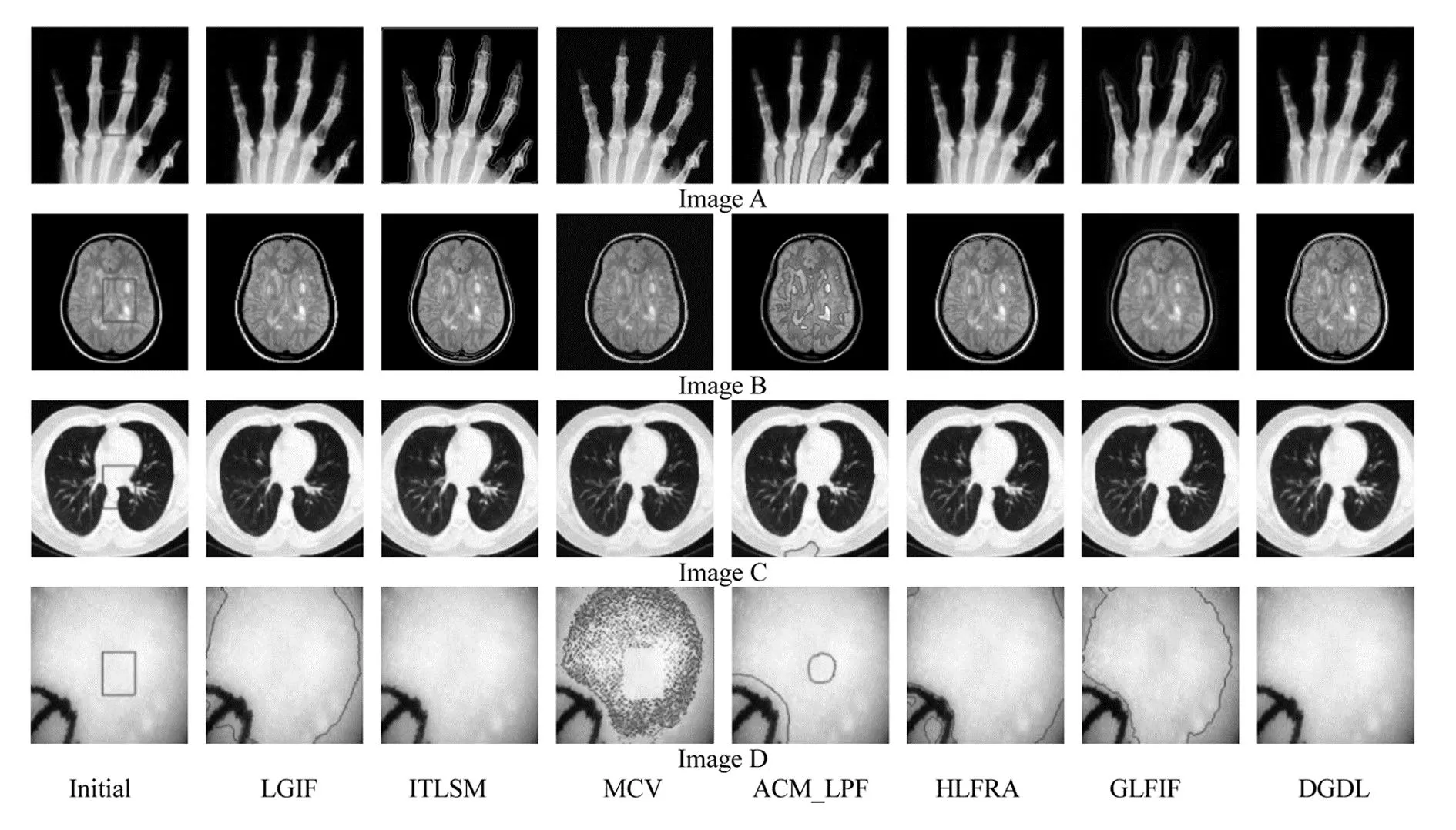
3.4 分割医学图像
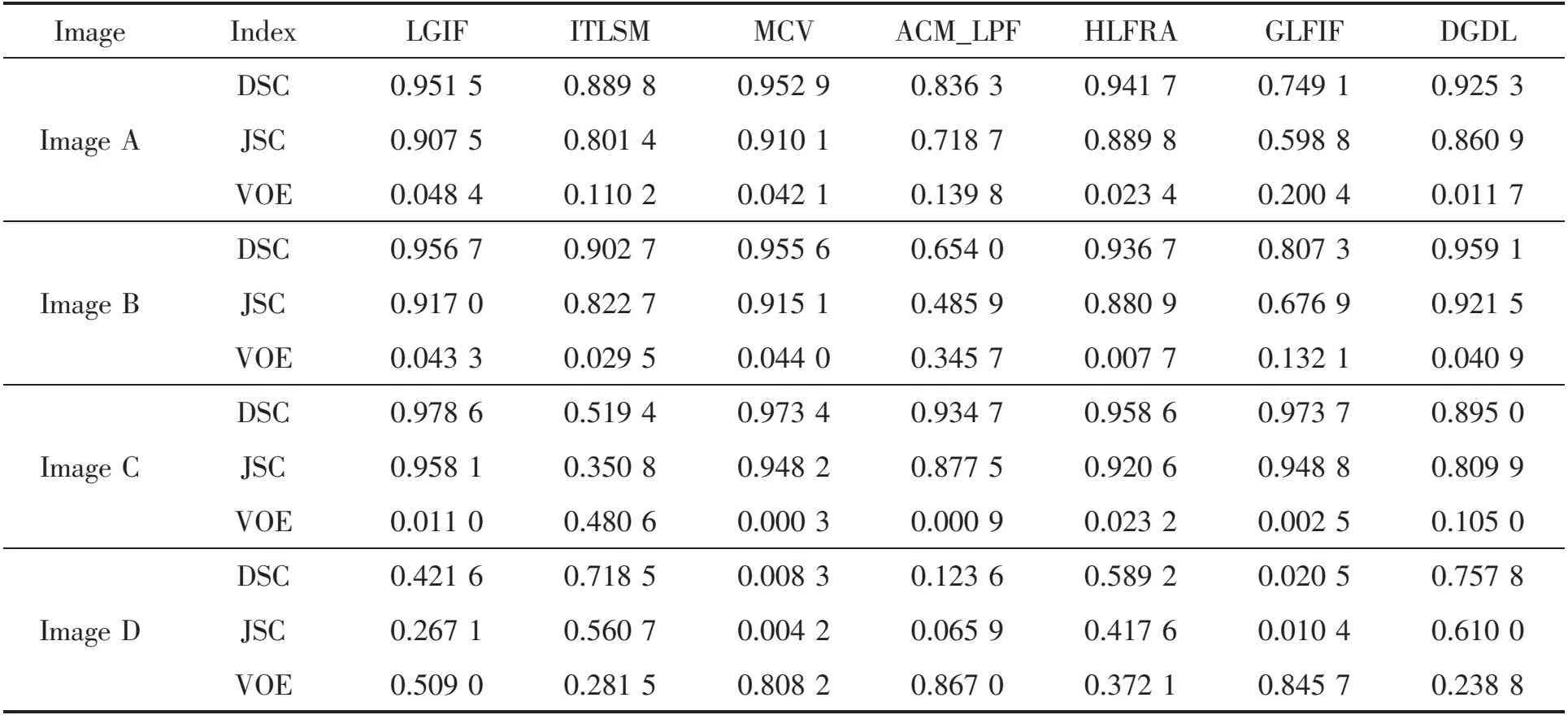
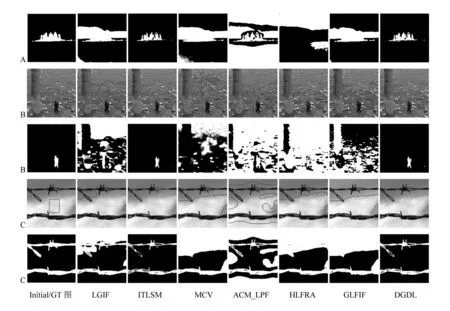
3.5 Weizmann数据集上的测试

4 结论
