蒋庄煤矿北十采区3号煤层构造复杂程度评价
2024-01-02王自国朱利岗王安民曹代勇宁树正宋忠亮
王自国,朱利岗,王安民,曹代勇,宁树正,宋忠亮,郭 强,刘 悦
(1.中国煤炭地质总局勘查研究总院,北京 100038;2.中国矿业大学(北京)地球科学与测绘工程学院,北京 100083;3.枣庄矿业(集团)有限责任公司,山东枣庄 277000)
0 引言
我国含煤盆普通遭受了强烈的后期构造运动改造[1-3],使得盆地边缘煤田的断层及褶皱极为发育,严重影响了煤矿的高效安全生产[4]。矿井地质构造的复杂程度对煤与瓦斯突出、矿井突水、冲击地压等问题至关重要,因此,矿井构造复杂程度的评价成了煤矿安全生产的重要工作之一[5]。
矿井构造复杂程度评价主要以不同构造分区单元进行,选择合理的评价指标,通过模糊综合评价法[6]、层次分析法[7]、灰色关联法[8]、人工神经网络[9]等方法进行计算,获得最终的评价结果。近年来,除断裂密度、断层强度、褶皱平面变形系数、煤层倾角变异系数等传统评价指标[10],研究者们提出了更多的评价指标,以期合理且全面地进行复杂度评价,如基于分形理论提出的分形维数[11]、断层走向指数[12]、断层活化程度[13]等,进一步完善了矿井构造复杂程度评价体系。构造单元的划分以及合理的评价指标、评价方法的选取是不同地区矿井复杂程度精准评价的基础。
蒋庄煤矿位于山东省枣庄市,该煤矿断层较为发育,以走向NE 的地堑、地垒式构造组合为主[14],将矿区内主采煤层切割为走向NE 的狭长型断层构造。近年来,围绕着蒋庄煤矿的安全生产,研究者们在矿井突水、瓦斯防治,以及安全生产等方面提出了新的认识[14-18],但对构造复杂程度的评价却鲜少进行评价。本文选取矿区北十采区为研究区,选取合理的评价指标体系进行3号煤层的构造复杂度评价,为矿井的安全高效生产提供理论支撑。
1 区域地质概况
蒋庄煤矿位于滕南煤田的中部,地处华北板块鲁西南潜隆起区菏泽-兖州潜断隆的滕州潜凹陷内,属于鲁西诸多断块中的一个凹陷块体,就东西向构造带而言,它位于昆仑-秦岭纬向构造带的东延北支与新华夏第二沉降带的复合部位。矿井总体构造线呈NNE向展布(图1),形成以地堑、地垒为特点的宽缓褶皱区[14]。矿区内岩浆活动微弱,侵入时代在晚侏罗世之后燕山期,对煤层、煤质影响较小。矿区内含煤地层为石炭系—二叠系月门沟群太原组及二叠系月门沟群山西组。含煤地层平均总厚为310m,共含煤19 层,煤层平均总厚8.96m,其中3号煤层全区可采。
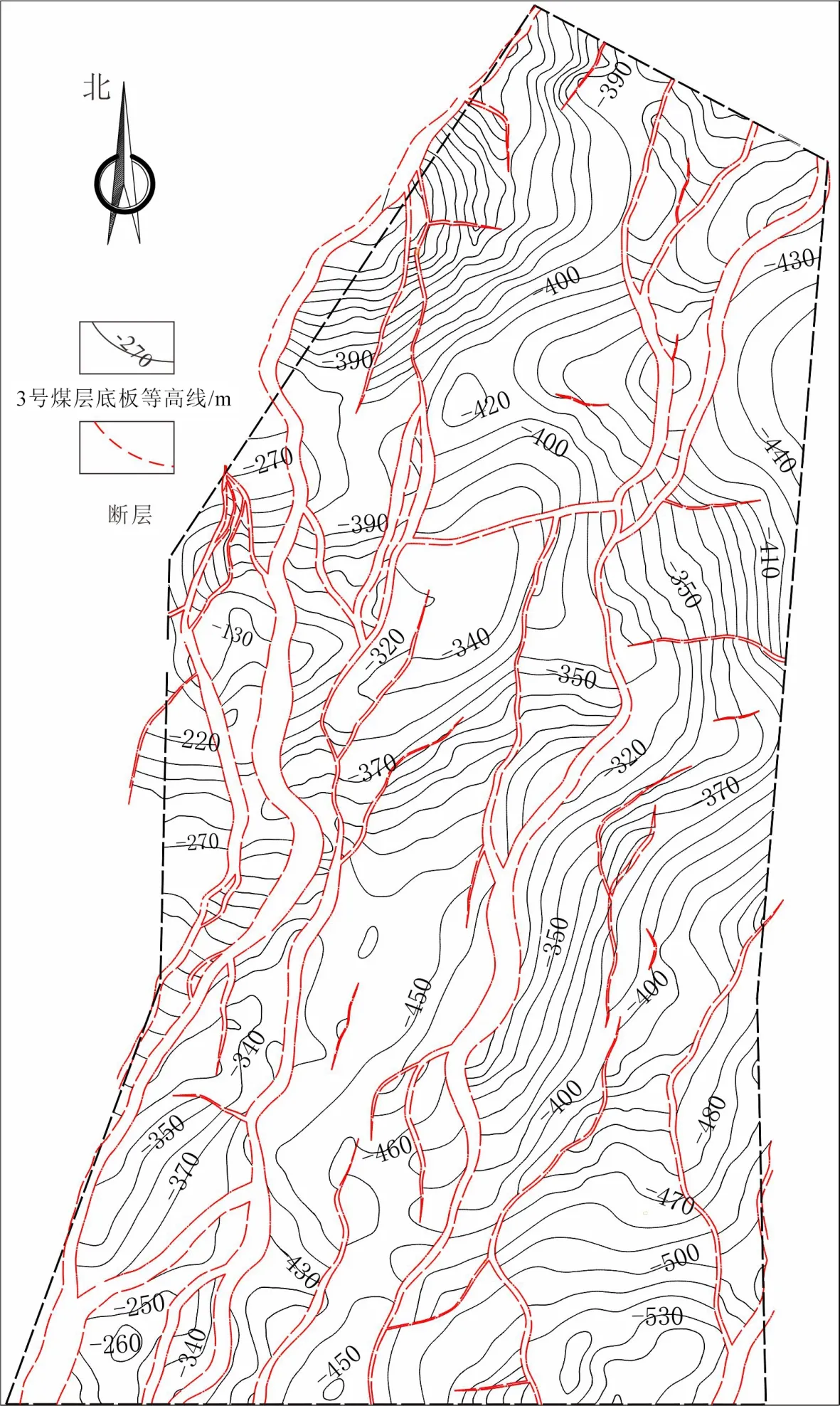
图1 研究区3号煤层构造纲要图Figure 1 Structural outline map of No.3 coal seam in the study area
2 评价单元划分与评价指标
2.1 评价单元划分
评价单元划分是构造复杂程度定量评价的基础,也是首要工作。传统来讲,单元划分多以大型构造边界、自然地理边界为限,但研究区构造相对复杂,无论是以大型断层边界或自然地理边界均无法进行合理划分,因此,对研究区采用网格状均匀分布的方式确定评价单元,以北十采区3下煤底板等高线图为底图,以400m×400m 为单元,将北十采区划分为40 个评价单元,覆盖于可采煤层之上,编号1~40,作为本次评价的基本单元(图2)。

图2 评价单元划分Figure 2 Evaluation unit division
2.2 评价指标
评价指标的合理选取是构造复杂程度准确与否的重要前提,每一个评价指标须完整地反映研究区构造发育情况,并以定量的形式表现出来,使之可以相互比较,同时,各个指标间应互相弥补,选择的所有指标可以全面地定量表征地质构造的复杂程度。通过对矿井构造发育特征的分析,结合前人的研究成果,本次研究综合选定矿井构造定量评价指标中的断裂分维值(D)、断层强度(F)、断层密度(M)、褶皱平面变形系数(K)、煤层倾角变异系数(S)5个指标为本次评价用指标。
2.2.1 断裂分维值(D)
分形理论在近年来发展较为迅速,容量维(又称盒维数)、信息维、多重分形相继被应用于构造地质分析[19]。断裂在地质体上的参数可以长度、数量、规模、组合形式进行表征,这些具有构造涵义的参数在不同尺度条件下被证明具有相似性[20-21]。分形维数逐渐被用于地质断裂特征属性,相似维(D)是应用最多的一种分维,对于某一具有自相似性的地质体断裂系统,则定义相似维:
式中:N为划分的单元数量;r为每一单元与整体的相似比。
分维值包含断裂长度、数量及组合关系等信息,是一项综合性的指标。断裂信息越复杂,其对应的分维值就越大。计算断裂分维值的具体有很多,如码尺法、康托尘集法和网格覆盖法等,其中最常用的方法是网格覆盖法[22],本次同样也采用网格覆盖法进行断裂分维值的计算,具体步骤如下。
1)如图3所示,在划分的标准单元格r0=400m的基础上,以r=r0/2 将标准单元格均分为4 个单元格,并数出含有断裂的单元格数量,即N(r)。以此类推,分别设定r值为r0/2、r0/4、r0/8,将网格尺寸不断按倍数缩小,从而得到相对应的N(r),直至将划分的单元格内的含断裂网格统计完为止。

图3 网格覆盖法示意图Figure 3 Schematic diagram of grid-coverage method
2)将步骤1)获得的N(r)与r值在lg(1/r)-lgN(r)坐标系中做相关性分析,如图4 所示,获得相关系数R2较高的线性公式,其斜率即为分维值D。最终求得各单元的分维值如表1所示。

表1 评价指标计算结果Table 1 Calculation results of evaluation indicators

图4 断裂分维值求解过程示意图Figure 4 Schematic diagram of fracture fractal dimension solution process
以各单元中心点为坐标,绘制出研究区断裂分维值等值线图(图5)。断裂分维值在中东部变化较大,在东北部变化较小,值也较低,说明东北部断层分布相对较为均匀,中东部断层分布差异较大。
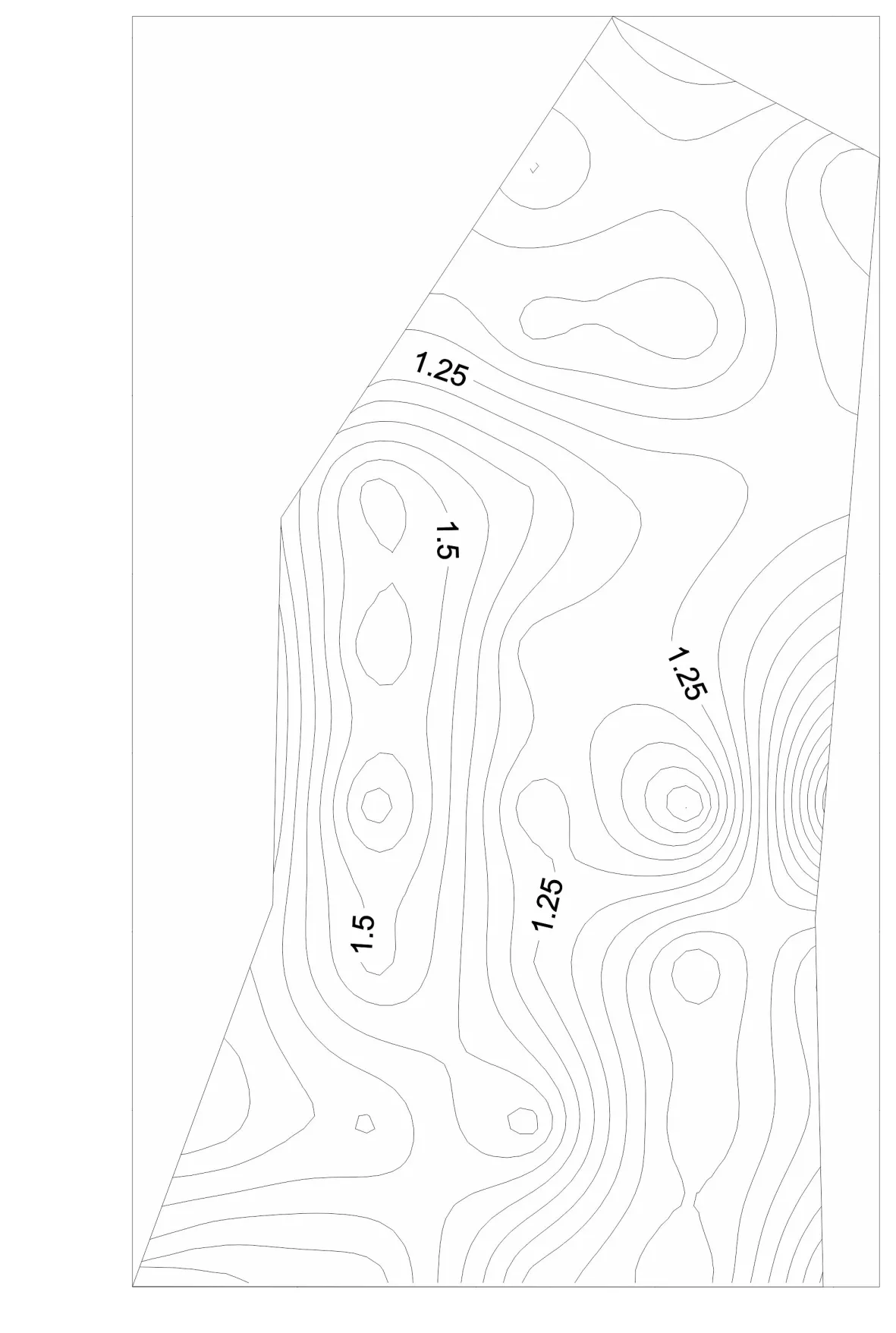
图5 断裂分维值等值线Figure 5 Contour of fracture fractal dimension value
2.2.2 断层强度(F)
断层强度用于表征不同单元内断层的发育程度,不同于断层密度仅能表示断层的数目,断层强度以划分的单元格内所有断层的延伸长度与其落差的乘积之和,来反映断层的综合复杂程度[8]。其表达式为
式中:li为断层的水平延伸长度,m;hi为断层的落差,m;S为单元格面积,万m2;n为断层条数,条。
按照公式依次统计出每个单元的断层强度,结果见表1。以各单元中心点为坐标,绘制出研究区断层强度等值线图(图6)。断层强度值在中西部较大,变化也较大,在中东部变化较小。

图6 断层强度等值线Figure 6 Contour of fault strength
2.2.3 断层密度(M)
在一定范围内,断层密度(M)可以直接反映断层的发育程度,能够反映断裂构造在空间分布中的密度,在研究断层的发育和分布时通常用它来进行定量分析和表征。单位长度或面积内断层的条数就是要量化的密度,它指示了断层的发育程度,其表达式为
式中:n为断层条数,条;S为单元格面积,km2。
按照公式3 统计出每个单元格的断层密度,结果见表1。以各单元中心点为坐标,绘制出研究区断层强度等值线图(图7)。断层强度值在西部较大,变化也较大,在中部及中东部变化较小,断层密度也较小。
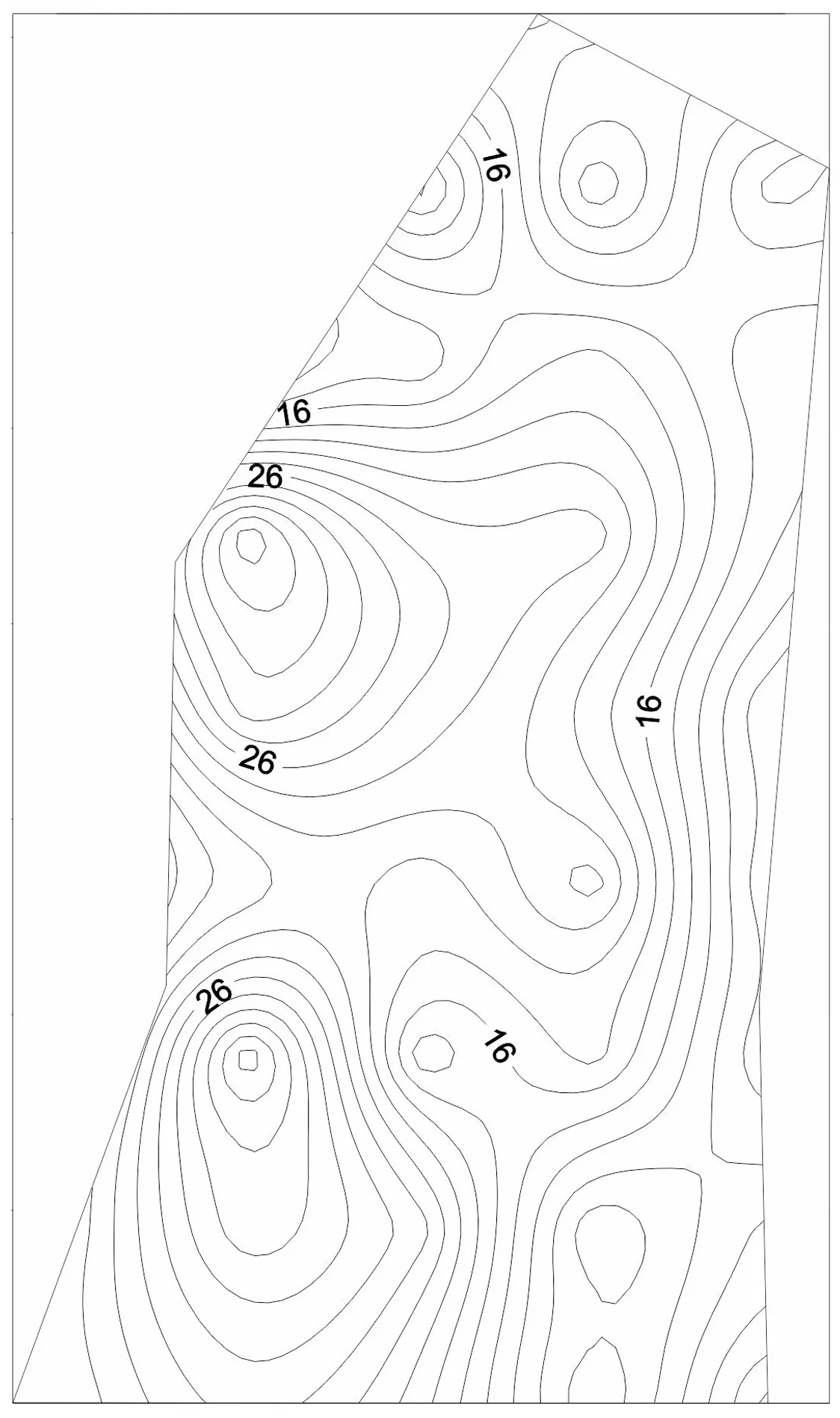
图7 断层密度等值线(条/km2)Figure 7 Contour map of fault density(number of pieces/km2)
2.2.4 褶皱平面变形系数(K)
褶皱平面变形系数(K)用于衡量褶皱的变形。蒋庄煤矿除断裂构造外,同样也发育较多的宽缓褶皱,与断层一样,需要在不同的构造单元内,对其进行变形程度的定量表征。褶皱构造发育越微弱,褶皱平面变形系数越小;反之,褶皱构造发育越复杂,对应的系数值就越大。其计算公式如下:
式中:h为相邻两条等高线的标差,m;L1为在单元内靠近单元中心的等高线的实际长度,m;L0为计算单元中心的两条等高线之间的水平距离,m;L2为在单元内靠近单元中心的等高线的割线长度,m(图8)。

图8 褶皱平面变形系数计算参数示意图Figure 8 Schematic diagram of calculation parameters of fold plane deformation coefficient
按照公式(4)统计出每个单元格的褶皱平面变形系数,结果见表1。以各单元中心点为坐标,绘制出研究区褶皱平面变形系数等值线图(图9)。褶皱平面变形系数在北部较大,变化也较大,在中部及南部变化较小,褶皱平面变形系数也较小。

图9 褶皱平面变形系数等值线Figure 9 Contour map of fold plane deformation coefficient
2.2.5 煤层倾角变异系数(S)
煤层倾角变异系数(S)指煤层倾角相对于统计单元内平均值的变化程度,反映了褶皱、断层等构造的发育情况,计算公式如下:
式中:ai为第i点的煤层倾角大小,°;为在单元格内煤层的倾角平均值大小,°;n为在单元格内煤层的倾角数量,个。
按照公式(5)统计出每个单元格的煤层倾角变异系数,结果见表1。以各单元中心点为坐标,绘制出研究区煤层倾角变异系数等值线图(图10)。煤层倾角变异系数在北部及西南部较大,变化也较大,在中部及中东部变化较小,煤层倾角变异系数也较小。

图10 煤层倾角变异系数等值线Figure 10 Contour map of coal seam dip variation coefficient
2.2.6 评价指标计算结果
评价指标计算结果如表1所示。
3 评价方法与评价标准
3.1 基于独立性权系数法的评价指标权重赋值
独立性权系数法是一种确定客观权重的方法。本次所选取的五个评价指标之间的信息存在部分信息重叠,重叠信息容易使得评价结果的准确度降低,对所选取的5 个评价指标进行独立性权分析是必要的[23]。
假设有m个评价指标X1,X2,X3,……,Xm,如果评价指标Xj若与其他指标之间的复相关系数(R)越大,表明评价指标Xj与其他指标之间的重复信息越多,则该评价指标的权重也就相对较小。计算公式为
式中:X为X的平均值;为X中除去Xj的剩余矩阵。
将原始数据进行归一化处理后,运用SPSS 软件,计算获得5个评价指标的权重如表2所示。

表2 独立性权重系数法确定的权重Table 2 Weights determined by independence weight coefficient method
3.2 评价标准及赋值
本次研究以前人工作为基础[22],确定本次评价标准如表3 所示,评价等级分A、B、C、D 四档,并对每一档进行赋值(以10分为满分),以线性关系对具体每一个值进行计算赋分。
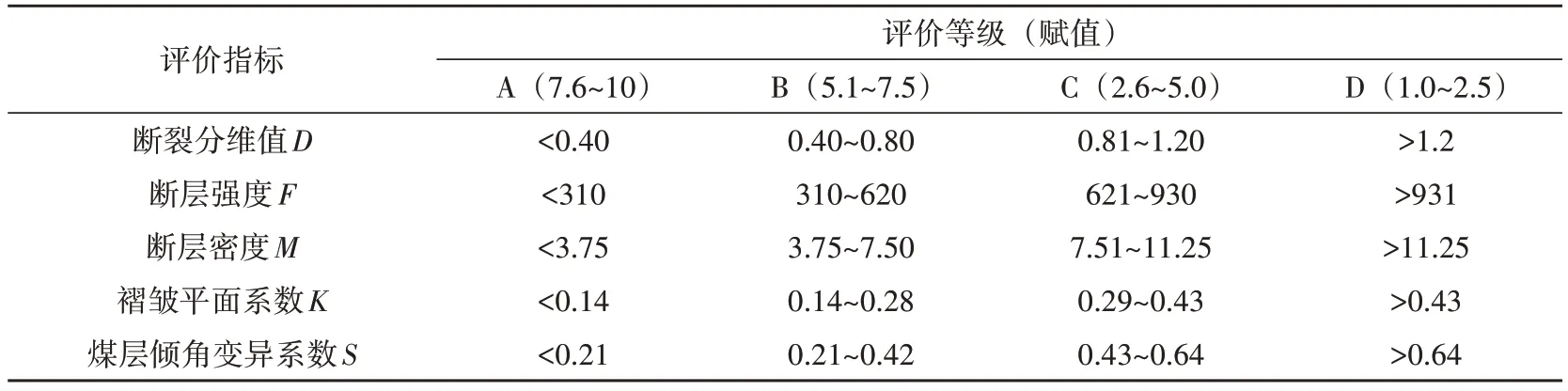
表3 评价标准及赋值Table 3 Evaluation criteria and assignment
4 评价结果
据表1、表3,对研究区内40 个分区单元进行赋值,再乘以表2中的权重系数,计算出每个分区单元的最终分值,并将大于6 分的定为I 级(构造简单),4~6 分的定为II 级(构造中等),小于4 分的为III 级(构造复杂),获得最终评价表4及评价等级图11。I级评价区块主要位于研究区中部的东西两侧,占比7.5%,II级评价区块占据了研究区大部分位置,占比高达70%,III 级评价区块主要位于研究区东北部和中西部,占比22.5%。

表4 研究区评价结果Table 4 Evaluation results of the study area
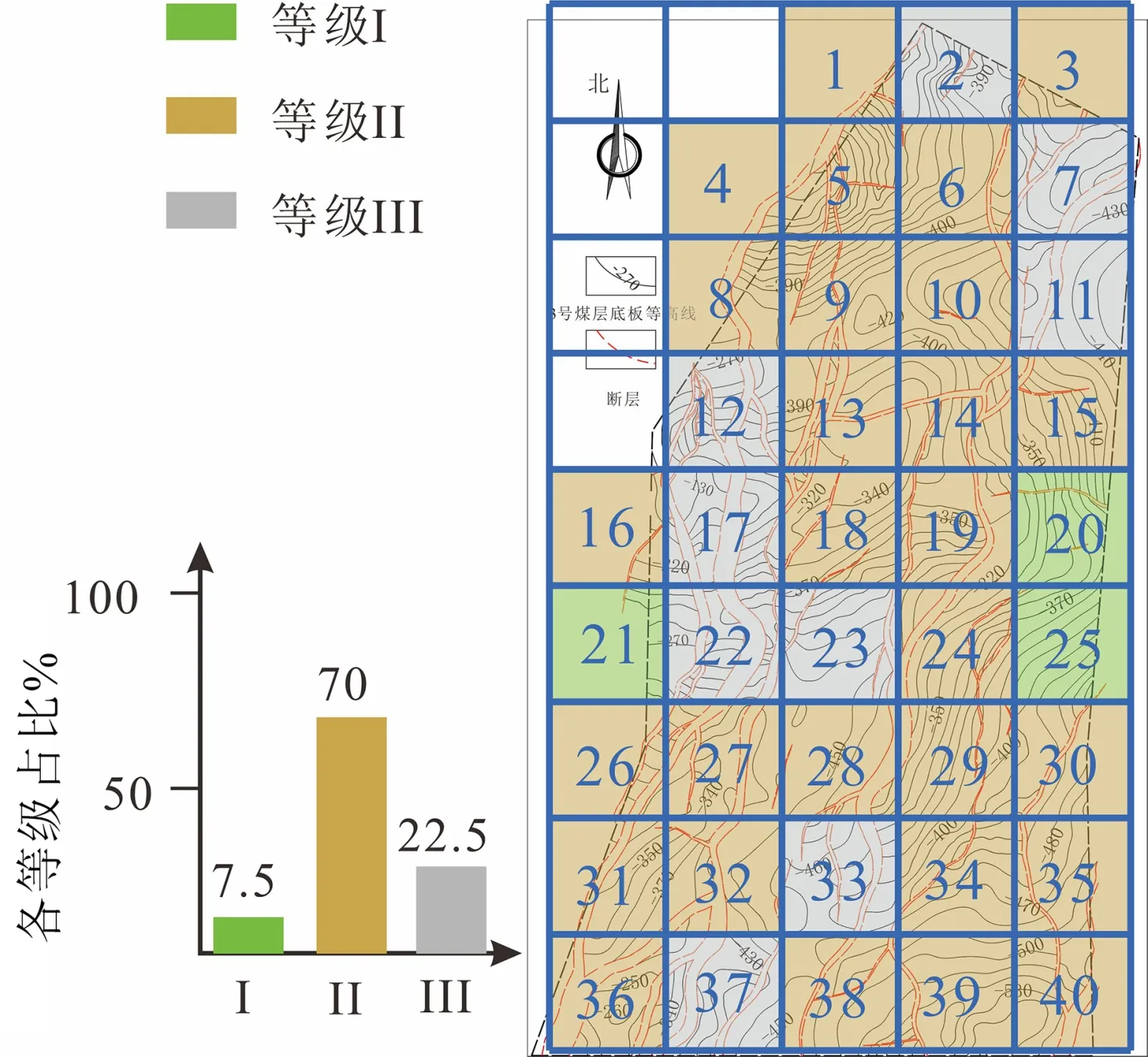
图11 研究区评价等级Figure 11 Assessment grade of the study area
5 结论
本次研究以蒋庄煤矿北十采区为研究区,以3号煤层为研究对象,综合选定断裂分维值、断层强度、断层密度、褶皱平面变形系数、煤层倾角变异系数5 个指标对3 号煤层构造复杂程度进行定量评价,结论如下:
1)3 号煤层断裂较为发育,东北部断层分布相对较为均匀,而中东部断层分布差异较大;断层强度值与断层密度以中西部为最,褶皱平面变形系数在北部较大,变化也较大,而煤层倾角变异系数则在北部及西南部较大。
2)以400m×400m 为单元,将北十采区划分为40 个评价单元,基于独立性权系数法对评价指标权重赋值,评价出构造简单级单元占比7.5%,构造中等级单元占比70%,构造复杂级单元占比22.5%。
