基于行程时间预测的城市车辆出行路径推荐方法

李晓玉,邢 雪

(吉林化工学院信息与控制工程学院,吉林 吉林 132022)

随着汽车数量逐年递增,部分一线城市交通拥堵已由中心城区向边缘城区扩散,给居民的工作生活带来诸多不便。行程时间可靠性对于良好的驾驶体验和保障顺畅的公共交通具有至关重要作用,因此,在考虑路网交通均衡的基础上,考虑车辆的行程时间,进行动态的路径推荐,可最大限度提高路网整体出行效率[1]。目前,诸多学者对路网复杂状况下车辆行程时间相关的路径推荐问题进行了大量研究。车辆出行路径选择问题是智能交通系统(Intelligent Transportation System,ITS)中出行者信息服务系统主要解决的任务,而动态交通信息的获取也是行程时间预测优化路径推荐的前提[2]。郭保青等[3-4]提出的基于优化蚁群算法的路径推荐模型,考虑了有障碍物的环境下临时规避障碍物,提高了寻路成功率。一些学者从最大路径可靠性和行程时间可靠性出发,提出应急车辆路径选择的优化方法[5-7]。另一些人提出结合A*算法和行程时间的搜寻实时最快路径的方法[8-9]。智路平等[10]使用行程时间可靠性作为关键控制变量,结合权值异化的Dijkstra算法,提高路径选择效率。白紫秀等[11]结合路网状态判别和行程时间,对私家车进行预约出行路径推荐。Shen等[12]构造了一种混合图结构,设计了考虑动态边权的最短旅行时间路径分析算法。综上所述,对于城市路网车辆路径选择问题,学者们多从行程时间、路网行程时间可靠性的角度研究,但对动态路网行程时间的预测和通过最短路径算法中求得的最短路径不一定最优等问题考虑不足。研究依托于吉林市自然基金项目,通过构建动态图卷积神经网络(DGCN)对路网各路段进行多时间步行程时间预测,根据出行需求并考虑避让拥堵区和均衡路网因素进行车辆出行路径推荐。

1 基于行程时间预测的区域状态识别

1.1 基于DGCN的路段行程时间预测模型

准确的行程时间预测是进行路径推荐的基础[2]。采用图神经网络对行程时间进行预测,特别是交通数据这种具备时空关系的特殊数据,可以很好地解决两个节点之间的相关性以及路网的复结构和动态性能的学习问题。因此,本研究采用动态图卷积网络(Dynamic Graph Conrolutional Nerwork,DGCN)模型对行程时间进行预测。模型主要包含拉普拉斯矩阵潜在网络(Laplacian Matrix Latent Network,即LMLN)模块和基于图卷积网络(Graph Convolutional Network,GCN)的交通预测模块。

拉普拉斯矩阵预测单元包括三部分:(1)特征采样:对每天最近15、30、45 min的数据进行采样,在减少特征的数据维度的同时对最近邻的交通数据进行采样;(2)空间注意力机制:为建立动态的交通路网的空间关系,采用注意力机制对路网当前近邻时间的邻接矩阵进行估计;(3)长短期记忆(Long Short-term Memory,LSTM)单元:通过LSTM单元提取时间和路网邻接矩阵序列的特征。

基于GCN的交通预测模块包含:(1)时间卷积层(Temporal Convolution Layer):主要包含四个卷积核为(1×ts)的二维卷积层,来提取数据中高维局部时间数据。(2)图时间卷积层(Graph Temporal Convolution Layer):将GCN与TCL堆叠为时空模块,集成GTCL模块[13]。

1.2 基于交通信息加权路网的区域划分模型

加载交通信息的路网满足复杂网络的基本特征,因此采用基于层次划分复杂网络的社区划分算法中的GN算法。GN算法效率较高,可将所有节点及边的有向关系考虑到网络划分之中,实验的划分结果具有层次性。路网分区结果的评判标准是模块度Q,见公式(1),模块度越大,则划分的社团结构也越明显[14]。

(1)

式中:m为网络中节点总数,个;v、w为路网中任意两个节点;Av、w为v、w两个节点之间边的权重;kw为节点w的度;kv为节点v的度;CvCw表示若v、w两节点在同一社团,则δ=1,反之δ=0。

加权GN算法的具体流程为:(1)初始状态下,每一个节点为一个独立的社区,即该状态下社区数与节点数相同;(2)忽略数据中边的权重,求所有边的边介数;(3)将边介数除以对应边的权重,得边权比;(4)移除边权比最大的边,计算当前网络的模块度Q;(5)对其余边重复步骤(1)到步骤(4),并计算每一步的边权比和模块度,直至网络中所有边均被移除;(6)运行结束,取Q最大时对应的社团划分数量和分区结果。

1.3 路网区域的动态交通状态识别模型

由公安部2020年颁布的《道路交通拥堵度评价方法》可得,区间路段交通拥堵度评价应采用平均行程速度[15]。路段限速为40 km/h时,区间路段平均行程速度与交通拥堵度的对应关系,如表1所示。

表1 限速40 km/h时平均行程速度与交通拥堵度的对应关系

(1)用该评价方法求某路段的平均行程速度Vi,如公式(2)所示。

(2)

式中:Vi为路网内第i条道路平均行程速度,km/h;n为路段的数量,个;ti为车辆i通过区间路段的时间,h。

(2)计算路网或某区域内道路平均速度V,如公式(3)所示。

(3)

式中:Vi为路网内第i条道路平均行程速度,km/h;n为路段的数量,个。

(3)根据区域平均速度结合平均行程速度与交通拥堵度识别关系,确定区域交通状态分级。

2 考虑拥堵区避让的路径推荐模型

为了量化城市路网中考虑避让拥堵区前后整体拥堵程度的变化,引入路网拥堵均衡指数概念。对于整个城市路网,在时间帧为t时段内,将路网拥堵均衡指数定义为一个二维向量:Mt[N,V],路网拥堵均衡指数M计算方式如公式(4)所示。

(4)

式中:N为路网中路段数量,个;Ti为基于DGCN预测所得的路段i的行程时间,h;Li为对应的路段i长度,km;a为归一化系数,算法中取10。

根据需求将最优路径问题可分为基于距离最短或权重最小,基于距离最短方法中又可分为自由路径和限制路径。本研究采用Flody算法,是解决任意两点之间的最短路径算法,可解决交通网络结构的最短路径问题,该算法的核心是通过局部最优求解全局最优,进行动态规划。首先寻找出目标OD的最短路径长度,然后记录下该长度的路径,即可寻找到推荐的路线;将路径中处于重度拥堵状态区域中的路段进行移除,再重复以上步骤,即可寻找到基于拥堵区避让的推荐路径矩阵和路由矩阵。

基于拥堵区避让的Flody算法流程如下。

(1)初始状态:根据DGCN预测所得的行程时间数据,求得图G初始基于行程时间的初始路由矩阵R0=[ri,j]n×n和邻接矩阵W。

(5)

(6)

(2)k=0:即对于每一对顶点vi和vj,途径顶点的下标≤k时,该路径可分为两段,即(vi,vo)和(v0,vj),这一长度就是两段路径的行程时间之和,比较这一新路径和路径(vi,vj),就可以确定vi到vj途经下标≤k的最短路径。

(3)k=1:同理,该路径可拆成(vi,…,vk)和(vk,…,vj)两段,当长度在k=0时就确定路径,再比较新路径和前面已知的路径(vi,vj),就可以确定途经下标≤k的最短路径。

(4)重复以上步骤,直到k=n-1为止,得到从vi到vj所有可能的时间矩阵和对应的路由矩阵。

(5)选取部分路径,去除其中有重度拥堵路段的边,组成新的路网图G1,重复步骤(1)～(4),得到基于避让拥堵区的时间矩阵和路由矩阵,得出对应的路径和行程时间。

3 实例验证

3.1 基于DGCN的行程时间预测结果

本研究所使用的数据集来源于安徽省宣城市中心城区公开卡口数据集,openITS平台整理发布,该区域内的总道路长度为174 km,包含2017年12月3日至9日全天的卡口过车数据和卡口GIS-T布点数据,卡口过车数据中一天的过车量数据大约有83万条,删除未识别的车牌号后数据量约74万条,筛选后数据量约56万条,日全天行程时间数据,包含一个交通特征即路段行程时间,在模型中将预测行程时间作为输出;时隙划分为15 min,每天的数据包含96个时隙,每小时所有数据有4个样本,因此设置T=4,模型中训练集、验证集、测试集的数量占比为3∶1∶1。

实验运用于Linux操作系统Ubuntu 18.04,GPU为RTX 3090×2,显存为48G,采用Python 3.7代码编写,模型架构采用基于PyTorch 1.2.0的深度学习架构进行开发。在图卷积和时间卷积中使用4个1×3的卷积核,预测时间步长c为12,学习率设为0.000 5,每一轮的衰减率为0.92,批次大小为8,使用l2_loss为损失函数,利用Adam作为优化器,在GTCL中设置切比雪夫多项式M=3,卷积核ts=3,多头注意力机制k=4,预测时间间隔Tp=12。

为估计不同输入的影响,使用最近邻的数据建立输入矩阵,用DGCN_r表示。为了进一步评估不同拉普拉斯矩阵对GCN的效率,特别是GAT,实验将本方法与四种基于DGCN的其他方法进行了比较,其他方法分别为:(1)ASTGCN,其中使用了注意力拉普拉斯矩阵;(2)DGCN_Mask,使用了掩模拉普拉斯矩阵;(3)DGCN_Res,使用残差拉普拉斯矩阵;(4)5 dGCN_GAT,一种用GAT代替模型的空间特征层GTCL的方法。所有方法比较的性能指标为:平均绝对百分比误差(MAPE)、平均绝对误差(MAE)和均方误差(RMSE)。

在数据集上平均一小时交通预测精度如表2所示,结果表明,DGCN_Res模型的所有指标具有最佳性能。拉普拉斯潜在矩阵可以更好的提取道路网络的动态空间关,DGCN_Res模型用经验拉普拉斯矩阵代替了全局优化的残差拉普拉斯矩阵,故精度优于其他模型,预测未来12个时段的结果。

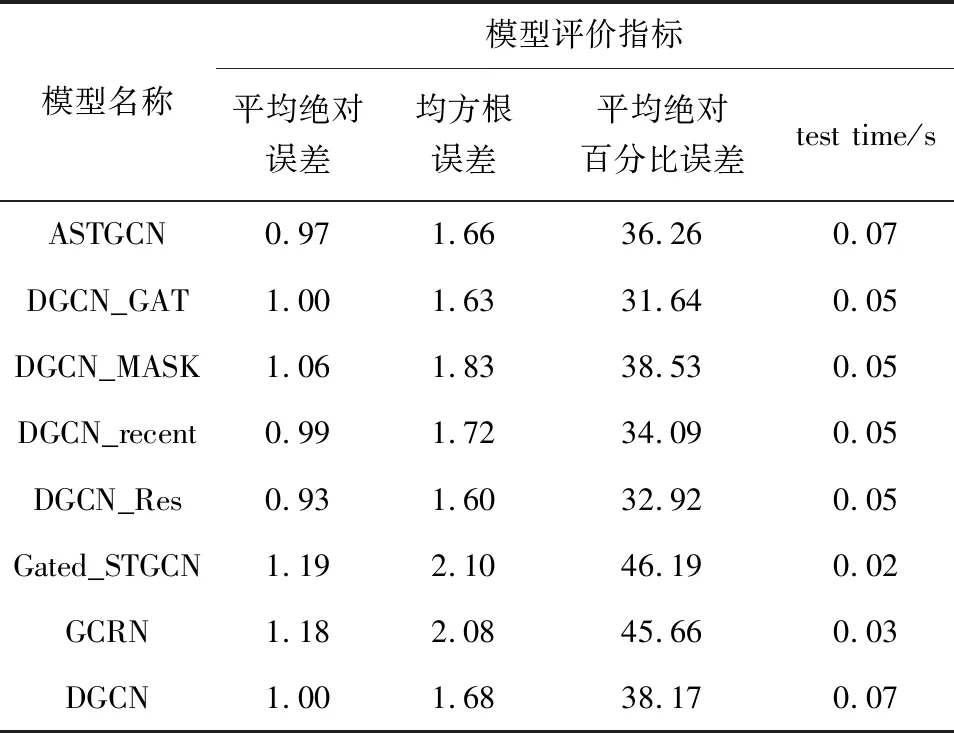
表2 预测精度结果

实验数据集来源于卡口GIS-T布点数据,其中包括39个卡口点,结合行程时间数据选取60个路段作为边,采用传统GN算法和加权GN算法对城市路网进行划分,不同分区数和对应模块度如表3所示。传统GN算法和加权GN算法,随着分区数量的增加,模块度都在逐渐降低,说明实际路网中,各边之间的相关性也在降低,结合拥堵区避让的条件和实际路网中路段相关度,选择分区数量为20,分区结果为[2,26,1]、[3,31,35]、[4,9,7]、[5]、[6,8,39,24]、[10,11,12]、[14,13]、[16,15]、[18,17]、[29,19,28]、[20]、[21]、[22]、[27,23]、[25,33]、[30]、[32]、[34,36]、[37]、[38],其中,加粗部分为重度拥堵区。根据分区结果,按顺序将区域划分为G1至G20,以便表示下一节拥堵区识别结果。

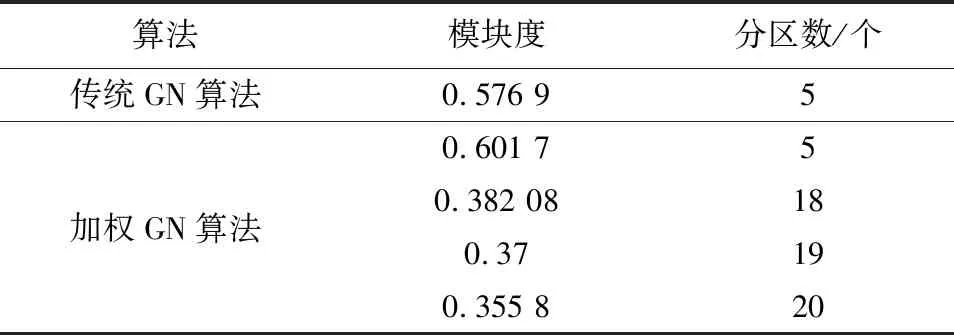
表3 加权GN算法分区结果

根据上一节行程时间预测的结果,可得预测的60个路段的行程时间数据,结合路网分区结果和区域状态识别的步骤,得重度拥堵区域为:G3、G4、G6、G8、G11、G12、G15、G16,中度拥堵区域:G1、G2、G5、G6、G9、G13、G18,轻度拥堵区域:G10、G15、G17、G20,畅通区域G14、G19,部分区域交通状态如表4所示。

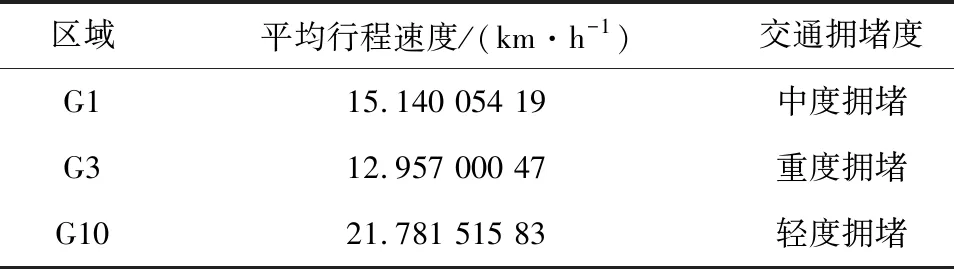
表4 区域状态识别结果

3.2 考虑避让拥堵区的路径推荐分析

初始状态下基于行程时间的路网邻接矩阵中,两点之间的权重代表基于DGCN预测未来15 min后该路段的行程时间,记为v(i,j)。依次遍历v(1,j)和v(i,1),比较v(1,j)、v(i,1)和v(i,j)的大小,如果v(1,j)+v(i,1)

若从敬亭湖公园附近卡口点19至档案局附近卡口点1,可由第39轮的邻接矩阵和路由矩阵得到所需时间和对应路径;通过去除拥堵区所在节点进行重度拥堵区的避让,也可得相对应的邻接矩阵和路由矩阵从而得到避让拥堵区的最短时间和路径,并对A、B、C三组路径进行展示。将初始最短时间路径和考虑避让拥堵区的条件下的路径、所需的时间和路网拥堵均衡指数进行对比,如表5所示。引入路网拥堵均衡指数作为考虑避让拥堵区前后路网拥堵状态对比的重要参数,可得在避让拥堵区的情况下,路网整体拥堵均衡指数降低,对重度拥堵区域的交通也有一定的缓冲。

表5 两种方法的路径推荐结果比较

4 结 论

出行路径仅考虑路径最短,可能造成交通网络关键区的拥堵;以当前交通状态进行路径诱导,可能出现车辆到达某路段时路段交通状态已经发生变化的情况。以实例中等城市路网为实验对象,对每天最近邻15 min、30 min、45 min数据进行采样,使用残差拉普拉斯矩阵的DGCN模型预测行程时间;通过加权GN算法结合实际路网情况进行分区,并根据平均行程时间识别区域拥堵状态;建立考虑拥堵区避让的路径推荐模型,对比不同方案的路网均衡指数,避让拥堵区前后路段,可在一定程度上降低路网全局拥堵状态。因而通过多时间步预测路段交通状态变化,再从全局考量针对已发生拥堵的区域进行避让推荐路径,一定程度上可减缓拥堵区的交通压力,对中型城市交通具有一定的借鉴意义。