基于ANSYS的深水栈桥钢管桩压弯稳定性计算

伍彦斌

(中铁五局集团机械化工程有限责任公司，湖南 衡阳 421000)

0 引言

在深水桥梁施工中，往往需要设置用于材料运输的临时栈桥[1-2]。为便于临时栈桥的安装和重复利用，其上部结构一般采用贝雷梁、型钢梁等装配式构件，下部结构一般采用钢管桩基础[3-4]。为满足安全适用、经济合理等要求，必须对栈桥结构进行详尽的力学性能分析与优化[5-7]。现有的临时栈桥结构分析方法中，钢管桩基础与桩周土体相互作用的模拟方法主要有两种[8-10]：一种是虚拟嵌固点法，一种是土弹簧法。虚拟嵌固点法，是假设钢管桩在虚拟嵌固点位置处固结，并忽略该嵌固点以上部分土体的约束和支撑作用，以简化边界条件；其中虚拟嵌固点的深度一般为桩的相对刚度系数T值的1.8～2.2倍[9-11]。土弹簧法，是通过对钢管桩的入土段进行较细致的网格划分，然后在钢管桩节点处建立“土弹簧”，相应土弹簧刚度的计算有m法与p-y曲线法等方法[11-12]。

采用土弹簧法可以较为真实地模拟桩-土相互作用，计算钢管桩的应力、变形和屈曲稳定性，但由于采用多点弹性支撑，不能直接得到相应的计算长度和长细比，不便于依据现行《钢结构设计标准》[13]进行钢管桩的压弯稳定性验算，难以定量指导结构优化；而采用虚拟嵌固点法，在桩周土层种类超过2层的情况下，由于多个土层的等效m值计算难以实现，故存在很大的局限性。

针对这些问题，本文提出最值点嵌固法，基于ANSYS软件的APDL编制参数化建模与分析程序，进行栈桥下部结构计算；在后处理中，将各根钢管桩入土段中双向弯矩矢量和最大的节点作为等效嵌固点，根据等效的边界条件，确定钢管桩的计算长度，进行钢管桩的双向压弯整体稳定性计算，从而指导栈桥下部结构的定量优化。

1 钢管桩压弯稳定性计算方法

临时栈桥的钢管桩一般采用圆钢管，在上部结构荷载、汽车制动力、风荷载、流水压力、波浪力、潮汐力及船舶撞击力等作用下，钢管桩呈双向压弯受力状态[14]。根据现行《钢结构设计标准》，当柱段中没有很大横向力或集中弯矩作用时，双向压弯圆管的整体稳定性按式(1)计算[15]：

(1)

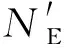
显然，根据式(1)，钢管桩的压弯稳定性计算，最关键的是确定其计算长度。对于临时栈桥，钢管桩的计算长度与入土段的约束情况、桩顶横联杆设置情况等有关。

图1为钢管桩最值点嵌固法示意。如图1(a)所示，在钢管桩的入土段内，随着入土深度增加，桩身弯矩矢量和呈先增大后减小的趋势，在深度Zm处达到最大值；入土深度增加到一定程度后，桩身的位移和转角不再发生明显变化，桩的受压承载能力也不再进一步提高。若仅取桩身弯矩矢量和最大值以上的部分分析，则其桩身弯矩布置图与在该最大值发生点嵌固时相近。因此，使桩身弯矩矢量和最大值与土弹簧法计算结果相等的等效嵌固点是客观存在的。

基于此，本文提出最值点嵌固法。如图1(b)所示，将钢管桩入土段中双向弯矩矢量和最大的点作为等效嵌固点，按照钢管桩顶端铰接、等效嵌固点处刚接的边界条件，确定钢管桩的计算长度，从而进行压弯稳定性分析计算。

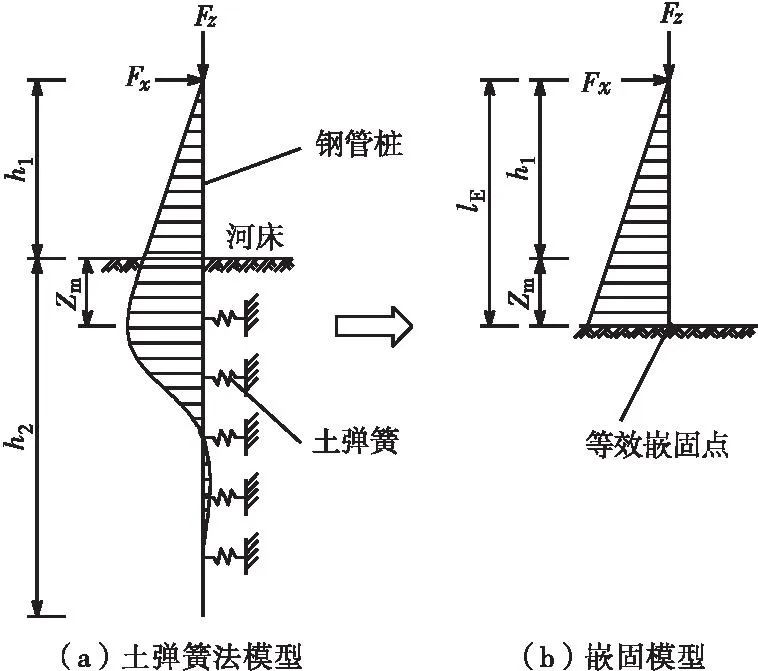
图1 钢管桩最值点嵌固法示意

在ANSYS后处理中，对于桩-土相互作用采用土弹簧法模拟钢管桩结构，采用最值点嵌固法进行压弯稳定性计算的数值程序如下：

1)针对单根钢管桩，执行*do循环，采用*get命令获取钢管桩入土段内各个单元的双向弯矩值，计算相应的双向弯矩矢量和，比较得到双向弯矩矢量和的最大值，并将双向弯矩矢量和最大值对应的单元编号和节点编号存入相应矩阵；

2)获取双向弯矩矢量和最大值对应节点的坐标，以该节点与钢管桩顶节点的距离作为该钢管桩的等效长度lE，并以该节点作为等效嵌固点，计算钢管桩的抗弯线刚度及桩顶横联杆和钢管桩的抗弯线刚度之比；

3)插值计算钢管桩的计算长度系数μ，再根据等效长度lE和计算长度系数μ，得到钢管桩的计算长度l0=μlE，并计算相应的长细比λ；

4)根据长细比λ插值计算钢管桩的整体稳定系数φ和钢管桩的欧拉临界承载力NE；

5)采用*get命令获取双向弯矩矢量和最大值对应单元的轴力Fx和弯矩My、Mz，计算等效弯矩系数β；

6)计算钢管桩双向压弯整体稳定应力值，并存入相应矩阵；

7)循环进行每一根钢管桩的双向压弯整体稳定性计算，并导出计算结果，根据计算结果，对每一根钢管桩的管径和壁厚进行优化调整，使所有钢管桩的双向压弯整体稳定性满足规范要求。

本程序中所采用的计算长度系数μ和稳定系数φ等原始数据表均通过读入txt文档的方式存储在相应的矩阵中。

2 单桩算例分析

某钢管桩采用φ820×10 mm螺旋钢管，总长30.0 m，弹性模量Ep=2.06×105N/mm2，钢材牌号为Q235，桩顶荷载为：纵向力5 kN，横向力10kN，竖向力800 kN，纵弯矩2 kN·m，横弯矩-1 kN·m。为比较传统的虚拟嵌固点法与本文最值点嵌固法的计算结果，建立如下3个有限元模型：

模型1：桩-土相互作用采用土弹簧模拟，土弹簧的刚度采用m法进行计算，为使桩的入土部分处于完全嵌固状态，桩的入土深度为20.0 m。

模型2：传统的虚拟嵌固点法模型，钢管桩在入土深度为2.0T处固结。

模型3：本文所提的最值点嵌固法模型，钢管桩在入土段弯矩矢量和最大值处固结，该模型必须在模型1计算完成后建立。

上述3个有限元模型的网格划分完全相同，单元划分长度取0.1 m，桩周仅考虑一层土，土的m值在3～120 MN/m4范围内变化。

单根钢管桩主要计算结果见表1，以模型1的计算结果作为标准解，表中相对差1表示模型2计算的最大弯矩矢量和与标准解的相对增量，相对差2表示模型3计算的最大弯矩矢量和与标准解的相对增量。钢管桩的嵌固深度计算值随桩周土m值的关系曲线如图2所示，钢管桩入土段弯矩矢量和最大值随桩周土m值变化的关系曲线如图3所示。

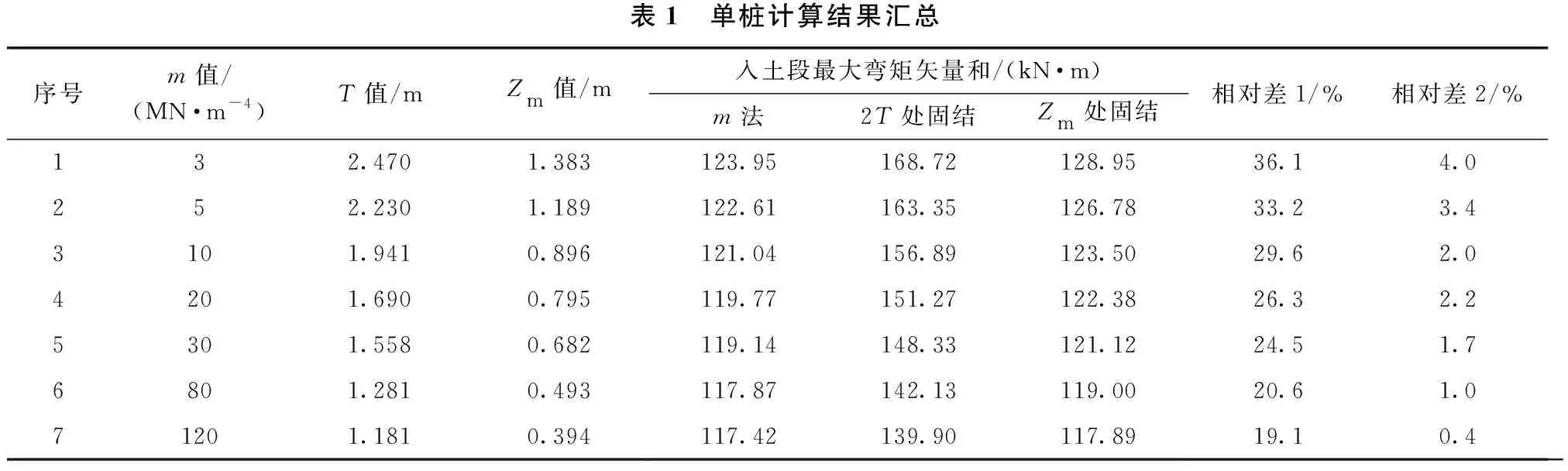
表1 单桩计算结果汇总序号m值/(MN·m-4)T值/mZm值/m入土段最大弯矩矢量和/(kN·m)m法2T处固结Zm处固结相对差1/%相对差2/%132.4701.383123.95168.72128.9536.14.0252.2301.189122.61163.35126.7833.23.43101.9410.896121.04156.89123.5029.62.04201.6900.795119.77151.27122.3826.32.25301.5580.682119.14148.33121.1224.51.76801.2810.493117.87142.13119.0020.61.071201.1810.394117.42139.90117.8919.10.4

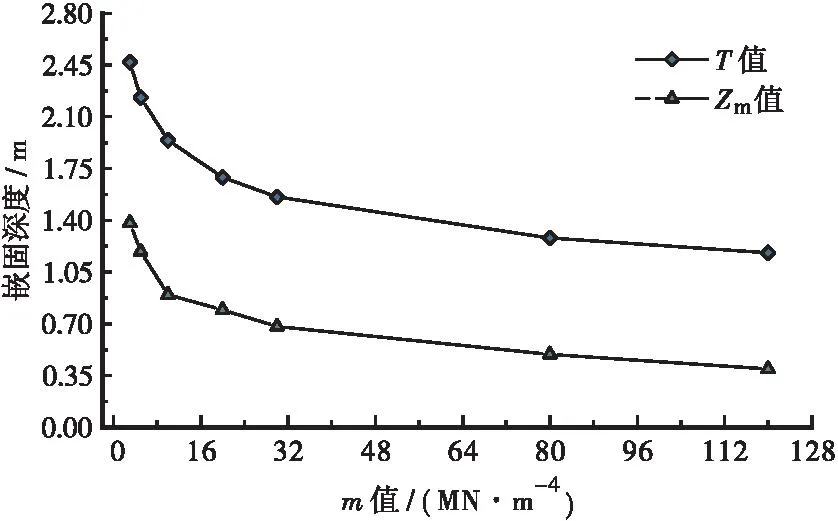
图2 嵌固深度关系曲线

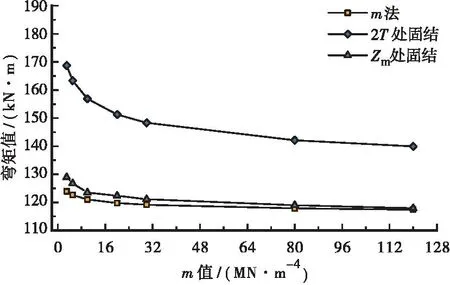
图3 最大弯矩矢量和关系曲线

由此可见，桩周土的m值越大，计算得到的T值和Zm值均越小，入土段的最大弯矩矢量和也越小，说明钢管桩的等效嵌固深度越浅。由于忽略钢管桩嵌固点以上部分土体的约束和支撑作用，故模型2和模型3的弯矩矢量和均比模型1的计算结果略大。

采用传统的虚拟嵌固点法模型，钢管桩入土段的最大弯矩矢量和计算值与标准解的相对增量为19.1%～36.1%，偏差较大，说明传统方法偏保守，这与已有相关研究结论相符[9]。

采用本文提出的最值点嵌固法模型，入土段的最大弯矩矢量和计算值与标准解的相对增量为0.4%～4%，偏差很小，且随着m值的增大，偏差越来越小，说明采用钢管桩入土段中双向弯矩矢量和最大的点作为等效嵌固点是可行的。

3 工程实例分析

3.1 工程概况

某跨越水道的特大桥(见图4)，全长862.0 m，平面位于R=1 800 m的圆曲线上，孔跨布置为(4×40.5)m+2×(3×40.5)m+(77+138+77)m+(3×40+35)m，主梁采用预应力混凝土连续刚构T梁和变截面连续刚构箱梁，桥墩采用柱式墩和薄壁墩，基础采用桩基础，最大桩径3.0 m，最大桩长93.0 m。桥址区属剥蚀丘陵间冲海积滨海地貌，地形起伏较大，桥梁桩基主要穿越杂填土、淤泥、粉质黏土、粗砂、卵石、残积砂质黏性土、砂土状强风化花岗斑岩、碎块状强风化花岗斑岩等8种土层。

桥梁所属海域为正规半日潮，每天两涨两落，20 a一遇最高潮位+4.95 m，理论最低潮面为-3.58 m，平均潮位+3.09 m。设计流速2.3 m/s，桥位最大水深约38.0 m，其中水深超过32 m的段落长度约300 m。为便于桥梁施工及两岸通行，需设计并建造一座临时栈桥。

3.2 临时栈桥设计方案

由于本栈桥不仅要为主桥桩基、承台施工提供进场通道，还要作为两岸连接的运输通道，故栈桥设置为两岸贯通，平面沿折线布置，栈桥全长约745 m，标准跨径15.0 m，小型渔船通航孔跨径18.0 m，按双向行车道设计，桥面宽8.0 m，栈桥桥面边缘距承台阻水围堰边缘的净距约1.5 m，栈桥横断面布置如图5所示。

图5 栈桥横断面布置(单位：m)

栈桥采用钢管桩基础，单排设置两根钢管桩，横向间距5.5 m，共计64排，根据钢管桩的总长度，分别采用φ820×10 mm、φ1 020×10 mm、φ1 220×12 mm和φ1 420×12 mm等多种规格；每隔3～4孔设一组制动墩，制动墩由双排钢管桩组成，纵向间距3.0 m；相邻钢管桩之间设置横联杆，当钢管桩直径不超过1.02 m时，横联采用φ426×6 mm钢管；当钢管桩直径大于1.02 m时，横联采用φ630×8mm 钢管。

钢管桩顶部设置承重横梁，承重横梁采用2-I56a双拼工字钢制作。纵向主梁采用贝雷桁架结构，除通航孔横向布置15榀贝雷梁外，其余横向布置12榀贝雷梁。贝雷梁上设置横向分配梁，采用I25a工字钢，纵向间距为0.75 m。横向分配梁上设置装配式桥面板，采用10 mm防滑花纹钢板，纵肋采用I12.6工字钢，横向间距为0.3 m。栈桥两侧设置护栏，考虑履带吊机工作高度，护栏高1.2 m。

为满足主桥施工需求，栈桥设计荷载标准参照公路I级荷载，在20 a一遇潮位和6级风力作用下，栈桥上允许135 t履带吊机走行并进行吊装作业(总重约180 t)；满足2辆12 m3混凝土搅拌运输车排队等候浇筑并与1辆空车错车的需求。

3.3 有限元模型与分析程序

由于栈桥长度较大，若建立全桥有限元模型，不仅建模工作量大，而且移动荷载计算工作量非常大，难以承受；若只选取3～5跨栈桥结构进行建模计算，由于钢管桩的截面规格类型较多，且钢管桩穿越的土层种类多，加之水深变化大，很难保证所选取的部分为全桥最不利结构。针对这些问题，本文将上部结构和下部结构分别进行计算，首先采用Midas进行标准上部结构的建模计算，得出作用在钢管桩顶部的设计荷载；再采用ANSYS进行全桥下部结构的建模计算，并采用最值点嵌固法对钢管桩的压弯稳定性进行分析。

限于篇幅，上部结构的计算过程不再赘述。根据上部结构计算，单排墩每根钢管桩的桩顶集中荷载为：竖向力1 550 kN，横向力5 kN；双排制动墩每根钢管桩的桩顶集中荷载为：竖向力1 400 kN，横向力5 kN，纵向力41.25 kN。

得出钢管桩顶部的设计荷载后，再采用ANSYS建立下部结构的有限元模型并进行计算。其中钢管桩入土深度、土弹簧刚度、钢管桩内力、钢管桩长细比、钢管桩压弯整体稳定性等全部采用APDL编制数值程序实现批量计算。本栈桥桩周各土层的m值及侧阻力标准值等计算参数如表2所示，栈桥下部结构有限元模型如图6所示。

图6 栈桥下部结构有限元模型

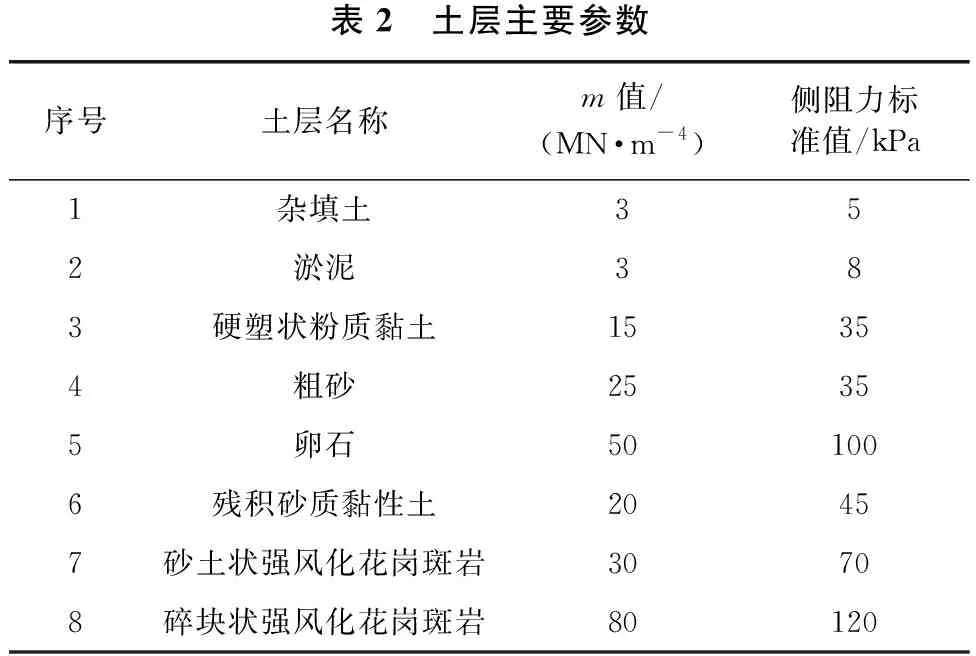
表2 土层主要参数序号土层名称m值/ (MN·m-4)侧阻力标准值/kPa1杂填土352淤泥383硬塑状粉质黏土15354粗砂25355卵石501006残积砂质黏性土20457砂土状强风化花岗斑岩30708碎块状强风化花岗斑岩80120

3.4 钢管桩稳定性计算

经过多次调整优化之后，临时栈桥全部128根钢管桩的长细比均未超过120，稳定应力均小于215 MPa，整体稳定性满足要求。

上游钢管桩的稳定应力计算结果如图7所示，下游钢管桩的稳定应力计算结果如图8所示，图中桩长仅为示意。

图7 上游钢管桩应力对比

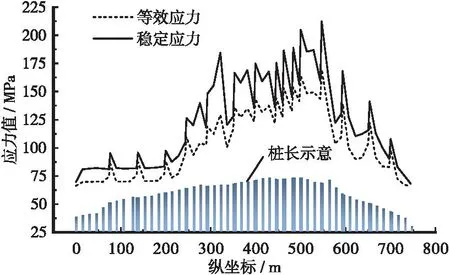
图8 下游钢管桩应力对比

在风荷载、流水压力、波浪力等横向力的作用下，上游侧钢管桩的轴向压力比下游侧钢管桩小，故在同一横排钢管桩内，下游侧钢管桩的等效应力和稳定应力均大于上游侧钢管桩；在汽车制动力作用下，制动墩前排钢管桩的轴向压力比后排钢管桩大，故前排钢管桩的等效应力和稳定应力均大于后排钢管桩。总体而言，等效应力和稳定应力最大值均发生在制动墩前排下游侧钢管桩。

钢管桩稳定应力分布的总体趋势是随桩长的增加而增大，但应力最大值并非发生在最长的钢管桩上。本栈桥钢管桩最大长度为50.5 m，共5排，其最大等效应力为137.4～164.0 MPa，其最大稳定应力为167.8～204.9 MPa；本栈桥钢管桩最大等效应力约169.5 MPa，最大稳定应力约212.4MPa，对应桩长为46.0 m，比最大桩长小4.5 m。因此，若选取部分结构进行计算，有可能导致遗漏最不利的情况。

4 结论

1)单桩算例分析表明，采用传统的虚拟嵌固点法计算，钢管桩入土段的最大弯矩矢量和与标准解的相对偏差为19.1%～36.1%；而采用本文提出的最值点嵌固法计算，相对偏差仅为0.4%～4%，说明采用钢管桩入土段中双向弯矩矢量和最大的点作为等效嵌固点是可行的。

2)桩周土的m值越大，钢管桩的等效嵌固深度越浅，传统方法和本文方法的计算结果与标准解的偏差均越小。

3)实桥算例分析表明，钢管桩稳定应力分布的总体趋势是随桩长增加而增大，但应力最大值并不是发生在最长的钢管桩上。因此，若选取部分结构进行计算，有可能导致遗漏最不利的情况。

4)本文确定钢管桩等效嵌固点的方法是根据“嵌固”的定义而得，计算结果可信，以此确定钢管桩计算长度后，通过控制容许长细比和稳定应力，可以实现对钢管桩的稳定性进行定量优化。