JKZ型电子探空仪基测箱校准结果的不确定度评定方法

韩玉婷,第五朋朋,汪 鑫,宋 媛,金红梅,郑甲炜

(甘肃省气象信息与技术装备保障中心,兰州 730020)

0 引言

高空气象观测的自动化是科技发展的必然趋势,随着探空仪的技术发展,JKZ型电子探空仪基测箱已替代GEZ10型且广泛应用于气象领域[1]。目前中国气象部门使用的电子探空仪基测箱(简称“基测箱”)具有外观新颖、使用方便、质量小、检测数据稳定可靠等优点。

针对JKZ型电子探空仪基测箱的量值溯源,目前暂无相应的检定规程或校准规范,全国各气象计量技术机构依据中国气象局气象探测中心2018年10月下发的《电子探空仪基测箱测试方案》对基测箱进行校准。校准结果的可信度受测量误差、校准环境、标准设备等影响,因此难以确定引入不确定度的大小[2-6]。针对这个问题,文章基于JKZ型基测箱的测量原理和校准方法,采用GUM法通过实例分别对温度、湿度、气压、电压4种参数的校准结果进行了不确定度分析和评定,为制定相应的校准规范提供理论依据。

1 电子探空仪基测箱简介

电子探空仪基测箱是一种综合性检测设备,使用干湿球法测定测试区的标准温度值和湿度值;使用气压传感器给出放球地点的地面气压标准值;使用湿敏电容传感器测定零点测试室的标准湿度值,符合气象要素测量值传递要求,用于对探空仪的温度、湿度、气压地面基值进行测定,确定探空仪是否符合施放要求。其结构原理如图1所示。

图1 电子探空仪基测箱结构原理图

2 不确定度评定方法

2.1 GUM法评定不确定度的一般流程

文章采用GUM法评定不确定度,其评定的一般流程如图2所示。

图2 GUM法评定不确定度的一般流程

2.2 数学模型

测量数学模型是指测量结果与其直接测量的量、引用的量及影响量等有关量之间的数学函数关系[7]。

根据实际校准方法,可以认为JKZ型基测箱4种参数的测量数学模型均为:

Δx=xi-xs

(1)

式中,Δx为示值误差;xi为被校对象示值平均值;xs为标准示值平均值。

则合成标准不确定度可表示为:

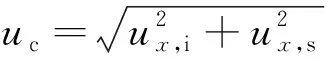
(2)

式中,uc为合成标准不确定度;ux,i为被校对象引入的标准不确定度;ux,s为标准装置引入的标准不确定度。

3 4种参数校准结果的不确定度实例分析

3.1 温度

温度标准器为标准铂电阻温度计,其准确度等级为二等。配套设备是直流测温电桥,其准确度等级为0.002级;液体恒温槽的温度均匀性≤0.02 ℃,温度波动性≤±0.02 ℃/10 min。

3.1.1 由被校对象引入的标准不确定度uT,i

在测试方案规定的环境条件下,将标准铂电阻温度计和基测箱温度传感器同时固定于同一液体恒温槽内中央等高位置,选择具有代表性的0 ℃和30 ℃温度点进行分析。调节液体恒温槽,分别设定温度测试点为0 ℃和30 ℃,当液体恒温槽温度达到设定值时,稳定15 min后分别读取并记录温度标准器示值和基测箱温度示值,每10 s读取1次,连续读取10次,分别用基测箱温度示值减去温度标准器示值得到单次示值误差,计算10次示值误差的平均值,用贝塞尔公式求得各校准点的示值误差及标准偏差如表1所示。

表1 被校基测箱在不同温度校准点上的示值误差及标准偏差 单位:℃

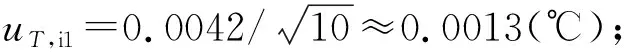
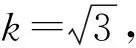
因被校对象示值重复性引入的标准不确定度小于其分辨力引入的标准不确定度,故uT,i=0.0029 ℃。

3.1.2 由二等标准铂电阻温度计标准装置引入的标准不确定度uT,s

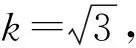
对于30 ℃校准点,由于操作在较高温度流动介质的恒温槽中进行,自热影响可忽略不计。

因测量二等标准铂电阻温度计的直流测温电桥准确度等级为0.002级,电阻相对误差不大于2.0×10-5Ω,对应温度相对误差不大于2.0×10-6℃,其标准不确定度uT,s3可忽略不计。

以上各项标准不确定度分量互不相关,则有:

(3)

0 ℃测试点uT,s≈0.0174 ℃。

30 ℃测试点uT,s≈0.0169 ℃。

3.1.3 合成标准不确定度uc及扩展不确定度U95

用公式(2)计算其合成标准不确定度为:0 ℃测试点uc≈0.018 ℃;30 ℃测试点uc≈0.017 ℃。

取包含因子k=2,则扩展不确定度为:0 ℃测试点U95=k·uc≈0.04 ℃;30 ℃测试点U95=k·uc≈0.04 ℃。

3.2 湿度

湿度标准器为精密露点仪,在测量范围-20～40 ℃露点最大允许误差为±0.15 ℃,湿度最大允许误差为±1.0%RH,分辨力为0.01%RH。配套设备是湿度检定箱,20℃时在有效区域内,湿度均匀度≤0.3%RH,湿度波动度≤±0.3%RH。

3.2.1 由被校对象引入的标准不确定度uH,i

在测试方案规定的环境条件下,将电子探空仪基测箱置于湿度检定箱内,并将精密露点仪探头和基测箱湿度感应部分(保持湿球纱布一直浸润在纯净水中)同时固定于电子探空仪基测箱测试区中央工作区域的等高位置上。调节湿度检定箱,设定湿度测试点为具有代表性的33%RH进行测试分析,当湿度检定箱内空气湿度到达测试点后稳定15 min,分别读取并记录湿度标准器示值和基测箱湿度示值,每10 s读取1次,连续读取10次,分别用基测箱湿度示值减去湿度标准显示值得到单次示值误差,计算10次示值误差的平均值,用贝塞尔公式得出示值误差及标准偏差如表2所示。

表2 被校基测箱在该湿度校准点上的示值误差及标准偏差 单位:%RH

由于校准结果为10次平均值,所以由被校对象示值重复性引入的标准不确定度uH,i1≈0.009%RH。

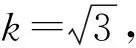
因被校对象示值重复性引入的标准不确定度小于其分辨力引入的标准不确定度,故uH,i=0.029%RH。

3.2.2 由精密露点仪标准装置引入的标准不确定度uH,s

在测量范围为-20～40 ℃时,精密露点仪露点的最大允许误差为±0.15 ℃,湿度最大允许误差为±1.0%RH。在环境温度为20 ℃、湿度为33%RH时,露点为3.3 ℃,则湿度最大允许误差为±1.0%RH,取正态分布k=3,则由精密露点仪的准确度引入的标准不确定度分量uH,s1≈0.33%RH。

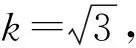
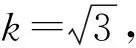
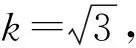
3.2.3 合成标准不确定度uc及扩展不确定度U95

用公式(2)计算其合成标准不确定度uc≈0.41%RH。

取包含因子k=2,则扩展不确定度U95=k·uc≈0.9%RH。

3.3 气压

标准器为数字气压计,分辨力为0.0001%FS,最大允许误差为±0.1 hPa。配套设备是气压发生器,扩展不确定度U=(0.02～0.04) hPa,k=2。

3.3.1 由被校对象引入的标准不确定度uP,i

选择常压点900 hPa作为校准点,使数字气压计与基测箱同时与气压发生器连接,调节气压发生器到达校准点,待稳定后,分别读取数字气压计和基测箱气压示值,每10 s读取1次,连续读取10次,分别用基测箱气压示值减去标准器示值得到单次示值误差,计算10次示值误差的平均值,用贝塞尔公式求得示值误差及标准偏差如表3所示。

表3 被校基测箱在该气压校准点上的示值误差及标准偏差 单位:hPa

由于校准结果为10次平均值,所以由被校对象示值重复性引入的标准不确定度uP,i1≈0.0010 hPa。

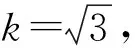
因被校对象示值重复性引入的标准不确定度小于其分辨力引入的标准不确定度,故uP,i=0.0029 hPa。

3.3.2 由气压标准装置引入的标准不确定度uP,s

数字气压计的最大允许误差为±0.1 hPa,取正态分布k=3,则由数字气压计引入的标准不确定度分量uP,s1≈0.033 hPa。

气压发生器的扩展不确定度为U=(0.02～0.04) hPa,k=2。取最不利值,则由气压发生器引入的标准不确定度分量uP,s2≈0.02 hPa。

3.3.3 合成标准不确定度uc及扩展不确定度U95

用公式(2)计算其合成标准不确定度uc≈0.039 hPa。

取包含因子k=2,则扩展不确定度U95=k·uc≈0.08 hPa。

3.4 电压

数字多用表扩展不确定度为U=(0.8～2.0)×10-6V,k=2。

3.4.1 由被校对象引入的标准不确定度uV,i

在测试方案规定的环境条件下,将基测箱供电输出线正压、负压接线端分别与数字多用表电压通道正压、负压接线端连接。打开基测箱设置电源界面,选取12 V作为校准点,设置输出电压值,打开输出电源开关,通过数字多用表读取输出电压值作为标准值,每10 s读取1次标准值和基测箱输出电压值,连续读取10次,分别用被校基测箱输出电压示值减去标准器示值得到单次示值误差,计算10次示值误差的平均值,用贝塞尔公式求得示值误差及标准偏差如表4所示。

表4 被校基测箱在该电压校准点上的示值误差及标准偏差 单位:V

由于校准结果为10次平均值,所以由被校对象示值重复性引入的标准不确定度uV,i1≈0.010 V。

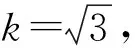
因被校对象示值重复性引入的标准不确定度小于其分辨力引入的标准不确定度,故uV,i≈0.029 V。

3.4.2 由数字多用表引入的标准不确定度uV,s

从数字多用表校准证书中得知数字多用表准确度引入的扩展不确定度U=(0.8～2.0)×10-6V,k=2。

U取最大值,则其标准不确定度uV,s=1.0×10-6V。

3.4.3 合成标准不确定度uc及扩展不确定U95

因数字多用表引入的标准不确定度远小于被校对象引入的标准不确定度,其不确定度可忽略不计。所以合成标准不确定度uc=0.029 V。

取包含因子k=2,则扩展不确定度U95=k·uc≈0.1 V。

4 结束语

JKZ型基测箱的不确定度评定需分别给出4种测量参数的不确定度,且电压校准结果的不确定度即为基测箱电压分辨力引入的不确定度。在文章所述测量条件下因分辨力引入的不确定度均大于示值重复性引入的不确定度,故在评定其他3种测量参数时忽略了基测箱示值重复性引入的不确定度,直接采用其分辨力引入的不确定度进行了评定。但因测量条件不一致可能会导致示值重复性引入的不确定度偏大,故文章的评定结果适用于基本满足上述测量条件的情况,当测量条件基本一致时可以直接引用上述结果,其余校准点可按照同样方法进行分析评定。