正常固结土层盾构隧道开挖对既有桥梁桩基的影响

2024-01-02刘新峰曹玉锋尹泽政

广东公路交通 2023年6期

刘新峰，曹玉锋，尹泽政

(广东华路交通科技有限公司,广东广州 510420)

0 引言

近年来公共轨道交通、地下管廊设施发展迅速,城市地下空间的利用越来越紧张。如广州地铁18号线、22号线、12号线、3号线东延线、13号线、珠三角水资源输水隧道等地下工程,无不涉及到盾构施工并行或下穿高速公路桥梁。其中18号线盾构施工距离高速公路桥梁桩基最小净距为1.54～5.30m;珠三角水资源输水隧道距离高速公路桥梁桩基净距5～13m;12号线隧道与高速公路桥梁桩基最小净距2m;13号线并行、下穿约2km高速公路桥梁桩基,与桩基最小净距为1.16m,并对高速公路桥梁桩基进行托换。隧道施工对高速公路桥梁结构的影响分析具有重要意义。

目前针对该问题的研究尚较少,主要采用有限元模拟、简化解析法、室内模型试验等方法。有限元模拟法将桩基与土体视为整体考虑,其刚度、接触较难定义,依据既有的试验数据来优化模型,使其能进一步预测其他类似工程桩基的变形和受力情况,模型的准确性主要依靠经验[1-2];简化解析法的主要思路是利用圆孔扩张理论、loganathan公式、H.G Poulos公式[3]计算隧道周边桩周土位置自由场的水平位移,再利用Pasternak地基模型将位移转化成作用在桩基上的附加应力,代入Winkler弹性地基模型,得到桩基的变形与弯矩;室内模型试验方法主要代表为离心机试验[4],但其试验均是在平面应变的前提下模拟隧道开挖,通过控制土体损失率来分析隧道施工对桩基的作用。

Winkler弹性地基模型与有限元模拟是未来发展的主流方向。目前,有限元模拟仍然在完善阶段。相比有限元模型建模的繁琐性与未知性,Winkler弹性地基模型受力明确、计算方便,在实际工程中更具有说服力,应用更广泛。近年来,许多学者也针对Winkler地基模型的不足,对模型进行优化调整,取得了一些研究成果,主要差异体现在位移与荷载、地基梁模型的选择上。

1 工程调查

目前在进行盾构隧道对桩基影响力学机制分析时,岩土层的水平位移以及应力变化的研究未考虑隧道开挖对土体扰动的影响,更忽略了盾构隧道开挖过程中的三维空间效应,使得土体水平位移与应力的分布规律与实际情况有较大差别。实际上,盾构隧道开挖对围岩的扰动以及土体损失均引起围岩产生变形,应力重分布,使得桩基两侧土层应力不平衡。土体位移的变化不仅与岩土层的物理力学性质,如弹性模量、泊松比相关,还与埋深、开挖洞径、土体损失率以及开挖后的空间效应等因素有关。通过调查近年来盾构施工的相关工程,得到盾构工程施工参数(表1)。

表1 盾构工程施工参数

由表1可知,地铁隧道埋深大致在20～30m之间,掘进速度0～50mm/min。盾构机盾壳外径略大于隧道管片外径,导致围岩与盾构隧道管片之间存在13.5～17.0cm厚的空隙体积,后续注浆将填充空隙体积。但由于注浆跟进不及时、注浆填充不到位、浆液凝结需要时间等原因,空隙体积会随着围岩应力的释放被压缩,该压缩量认为是土体损失量,通常用土体损失率来体现,即为土体应力释放与施工过程各种因素引起土体扰动的表征。土体损失率需根据土体性质、施工工艺以及工程经验选取。魏纲[5]、徐俊杰[6]、王占生[7]、卓普周[8]、季亚平[9]等通过分析各个城市地铁盾构施工引起地面沉降的实测数据,提出土体损失率η在0.20%～3.01%之间,对于黏土η通常为0.5%～2.5%,软土取1%～2%,并得到如表2所示的实际工程数据,其中约95%的实测数据分布在0.2%～2.0%[5-10]。

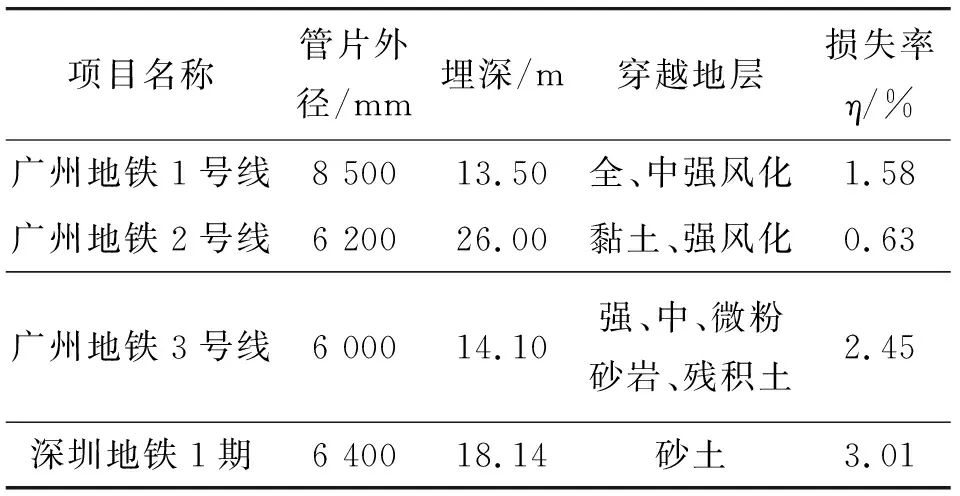
表2 盾构施工土体损失率

2 研究思路

为研究正常固结土层中不同因素下盾构施工影响范围与附近土体的水平位移规律,对不同围岩的弹性模量Es以及不同土体的损失率ν进行组合,分别选取土层弹性模量20MPa、30MPa、40MPa、50MPa。因工程中遇到的正常固结土体泊松比一般在0.25～0.35之间,故泊松比μ均取0.3。土体损失率ν分别取1.0%、1.5%、2.0%。共建立12个不同参数有限元三维模型。根据广州、深圳地铁隧道的数据(表1),模型中盾构直径R取6.3m,隧道顶埋深25m。模型计算范围为:长100m、高100m、厚度60m;模型边界为:顶部自由边界,左右施加水平方向的约束,底部施加竖直方向的约束,如图1所示。

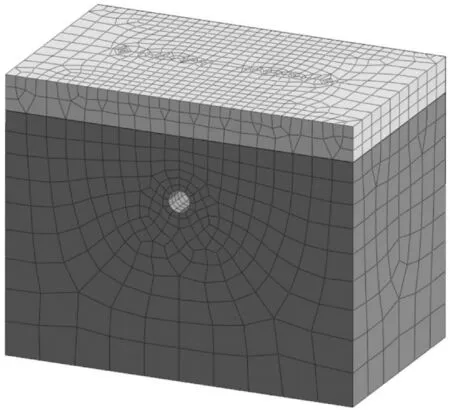
图1 计算模型

根据广州地铁21号线实际工程研究,隧道围岩应力释放是分阶段释放的,初次围岩应力释放率为20%～25%[11],因此模型中围岩初次应力释放取25%。土体损失率1.0%、1.5%、2.0%分别对应开挖界面径向压缩16mm、24mm、32mm。在隧道开挖界面与围岩之间设置软弱层模拟注浆填充,通过调节软弱层的弹性模量,实现隧道开挖界面径向压缩量,进而达到模拟相应土体损失率的效果。

首先提取各隧道模型地表以及隧道开挖界面两侧不同距离土体的水平位移进行分析,得到不同参数下围岩土体水平位移变形规律,并对土体位移分段拟合,建立考虑埋深、损失率、开挖洞径等因素的土体位移预测函数。然后确定围岩初始基床系数kh,利用力与位移的关系建立弹性地基梁力学模型。最后将计算结果与实测数据对比,使模型能够更好地预测临近桥梁桩基的变形与受力。

3 土体影响范围与变形预测

3.1 土体塑性区分析

以20MPa土体为例,不同土体损失率下的隧道围岩塑性区分布云图如图2所示。由图2可知,围岩塑性区围绕隧洞成弧形向外扩散,隧道腰部塑性最为严重,其次为拱顶外侧的围岩。土体损失率1.0%、1.5%、2.0%时,隧道腰部水平方向塑性区影响范围分别对应为8.00m、8.20m、8.61m,约1.3～1.5倍洞径。其中最严重的影响区域为洞口边缘2.5m范围,约0.4倍洞径;较为严重的区域为洞口边缘2.5～5.7m范围,为0.4～0.9倍洞径之间。因此,认为隧道开挖影响范围为隧道洞轴线上、下1.5R洞径范围,即H-1.5R洞径～H+1.5R洞径,H为洞轴线的埋深。

图2 20MPa土体塑性区分布云图

3.2 土体水平位移分析与预测函数的建立

由图3可知,沿竖直方向,土体发生水平位移的区域为地表至隧道轴线深度H+1.5R洞泾范围,水平位移突变区范围在隧道中性轴上、下1.5R洞泾范围。由图4可知,断面上隧道影响范围为开挖界面外1.5R洞泾范围。土体损失率1.0%、1.5%、2.0%分别对应开挖界面径向压缩16mm、24mm、32mm。本文根据各个深度位置的土体水平变形规律进行分析,建立土体位移预测模型。

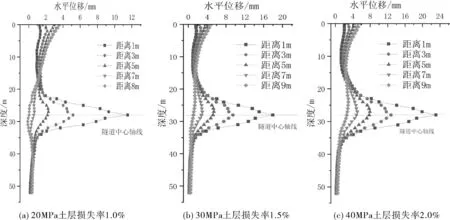
图3 土体位移曲线

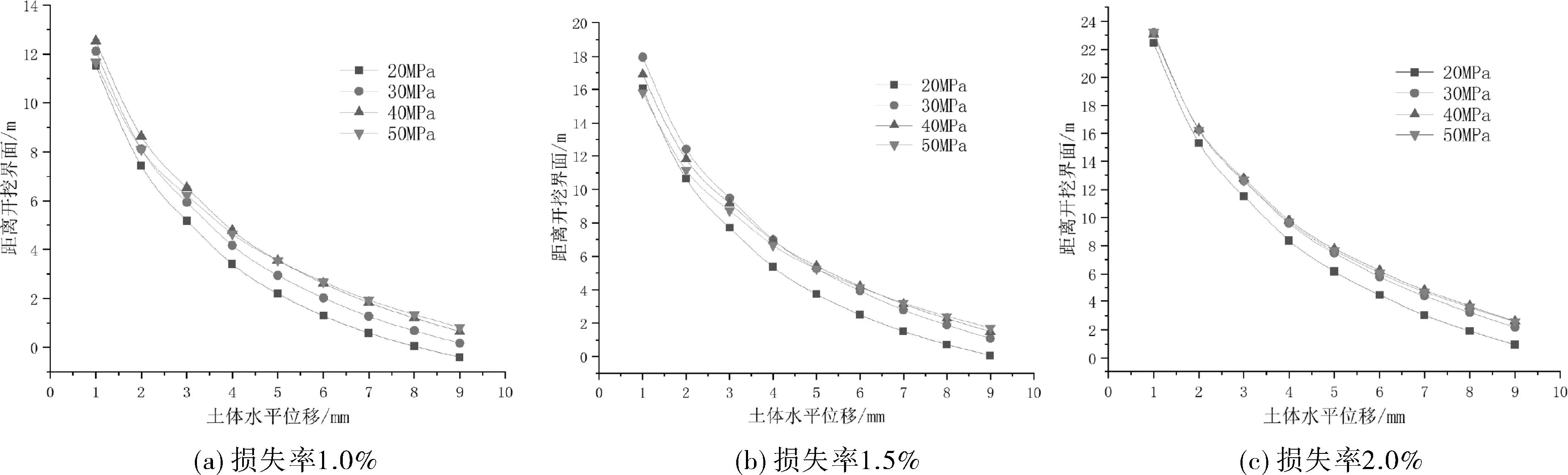
图4 不同损失率下隧道中心轴线径向方向水平位移

(1)地表土体水平位移随着与隧道轴线距离的变化,先是逐渐增大(包含1.5R洞泾对应范围),然后在开挖影响区内逐渐减小。1～8m范围,地表水平最大位移为3.24mm～6.00mm,为相应土体损失率对应径向压缩的18%～21%。利用matlab建立地表位移与损失率、径向压缩量的关系式,得到预测函数:

(1)

(2)H-1.5R洞径深度土体水平位移,损失率1.0%时,1～8m对应0.7～0.4mm;损失率1.5%时,1～8m对应0.9～0.6mm;损失率2.0%时,1～8m对应1.9～3.5mm,成曲线变化。建立该深度土体位移与损失率、径向压缩量的关系式,得到预测函数:

(2)

(3)H+1.5R洞径深度土体水平位移,损失率1.0%时,1～8m对应0.96～1.50mm;损失率1.5%时,1～8m对应1.30～2.35mm;损失率2.0%时,1～8m对应1.1～0.8mm。建立该深度土体位移与损失率、径向压缩量的关系式,得到预测函数:

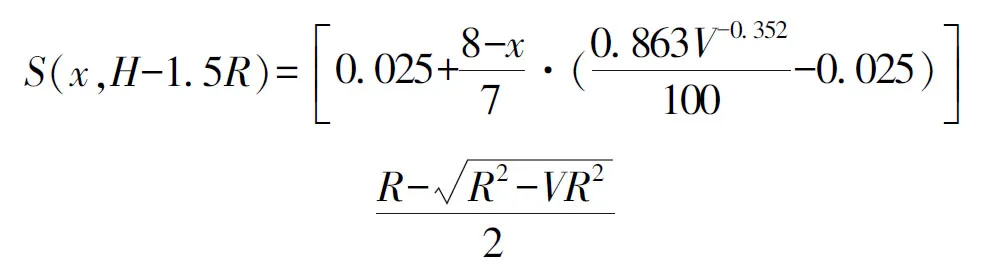
(3)

(4)隧道中性轴上、下1.5R洞泾范围,沿隧道轴线径向方向,水平位移呈现减小的趋势。根据3种损失率进行结果统计,得到隧道轴线径向方向不同距离土体水平位移与相应的径向压缩比值。不同损失率下,净距1m时,土体水平位移平均占比值为73%;净距2m时,土体水平位移平均占比值为50%;净距3m时,土体水平位移平均占比值为39%;净距4m时,土体水平位移平均占比值为29%;净距5m时,土体水平位移平均占比值为20%。不同土体的水平位移占比见表3。建立该深度位置土体位移关系式(式4)。

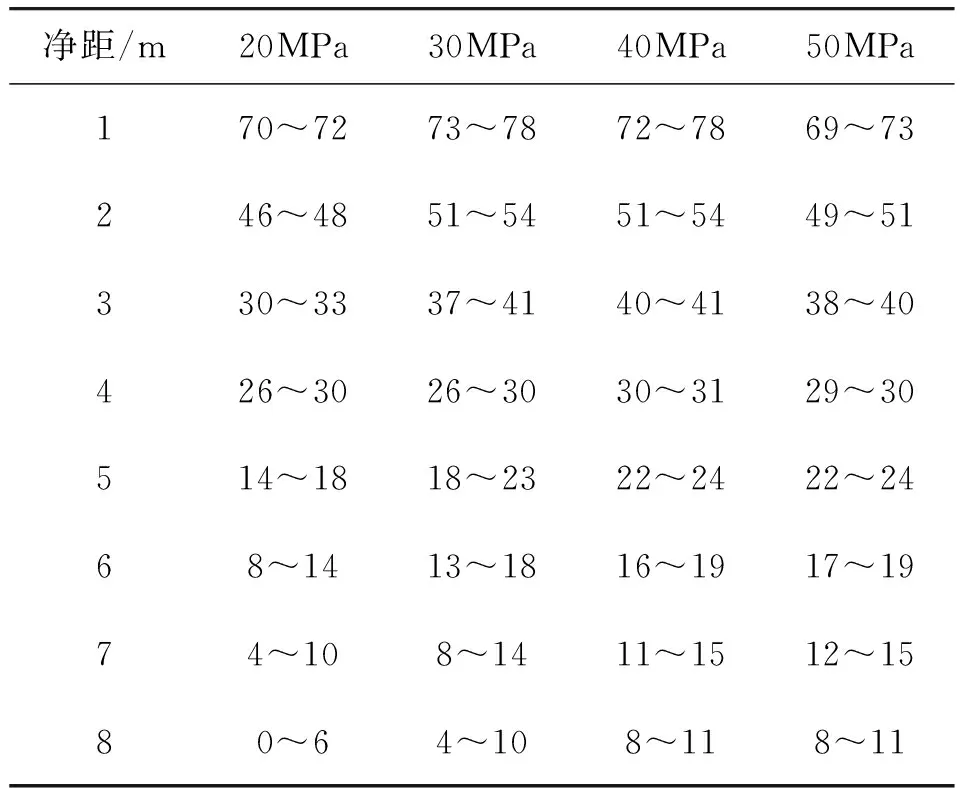
表3 沿隧道轴线径向方向的水平位移占比(单位:%)

(4)

结合式(1)～式(4),可以推得空间位置土体对应不同埋深H、开挖洞径R、土体损失率ν的位移预测函数式(5),其中x为与开挖边界的距离、H为隧道中心轴线与地表的距离、z为距地表的距离。由于H+1.5R洞径深度以下影响较小,故只考虑0～H+1.5R洞径深度范围。

(5)

以距离开挖边界1m为例,预测不同损失率下土体不同深度位置的水平位移。由图5可见,28m深度位置(中心轴线),损失率1.0%、1.5%、2.0%时分别对应水平位移11.5mm、17.9mm、23.1mm;对应预测位移值为12.2mm、18.3mm、24.4mm。预测模型与有限元模拟数据的拟合效果较好。

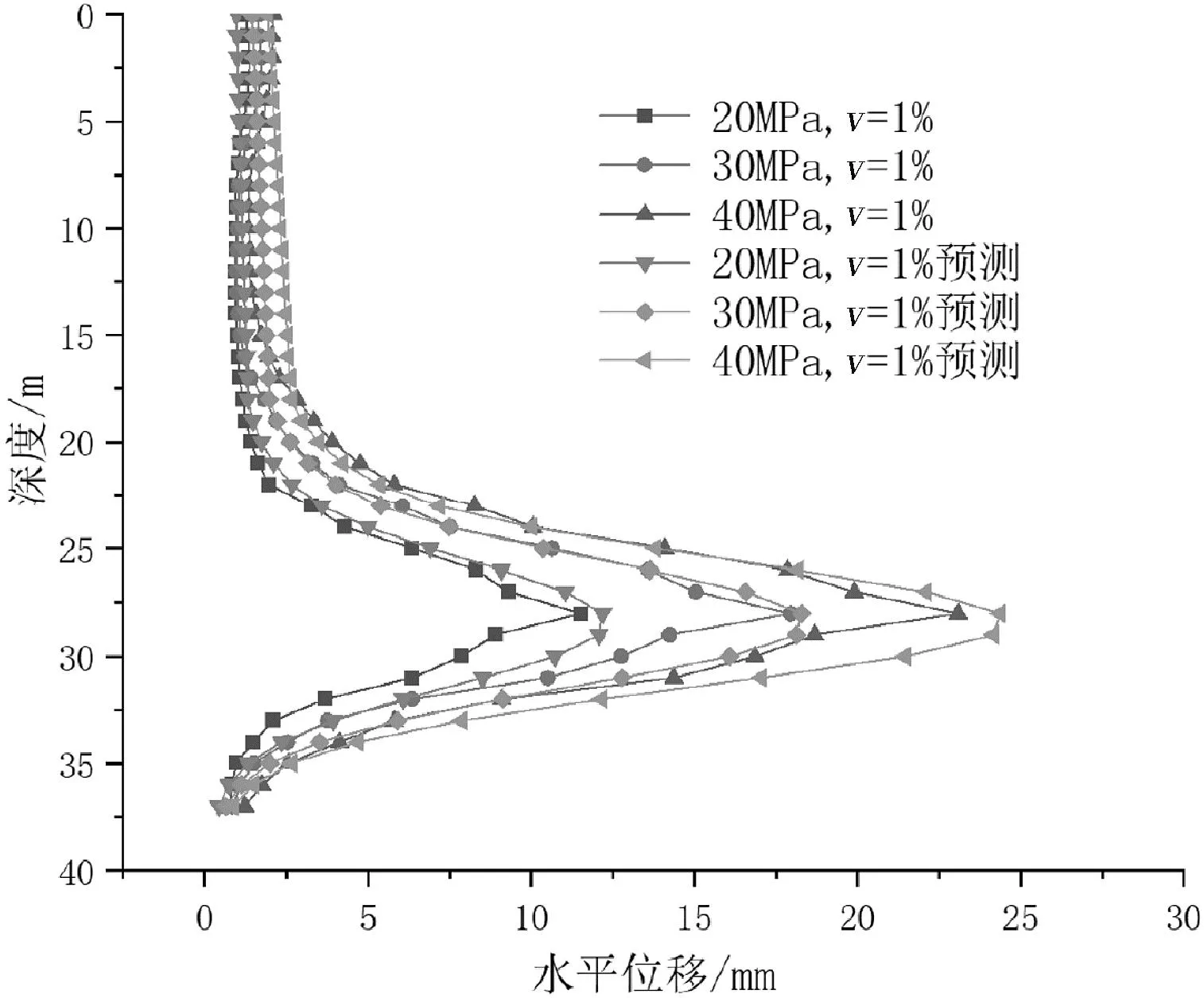
图5 不同损失率下x=1.0m距离时土层水平位移拟合效果

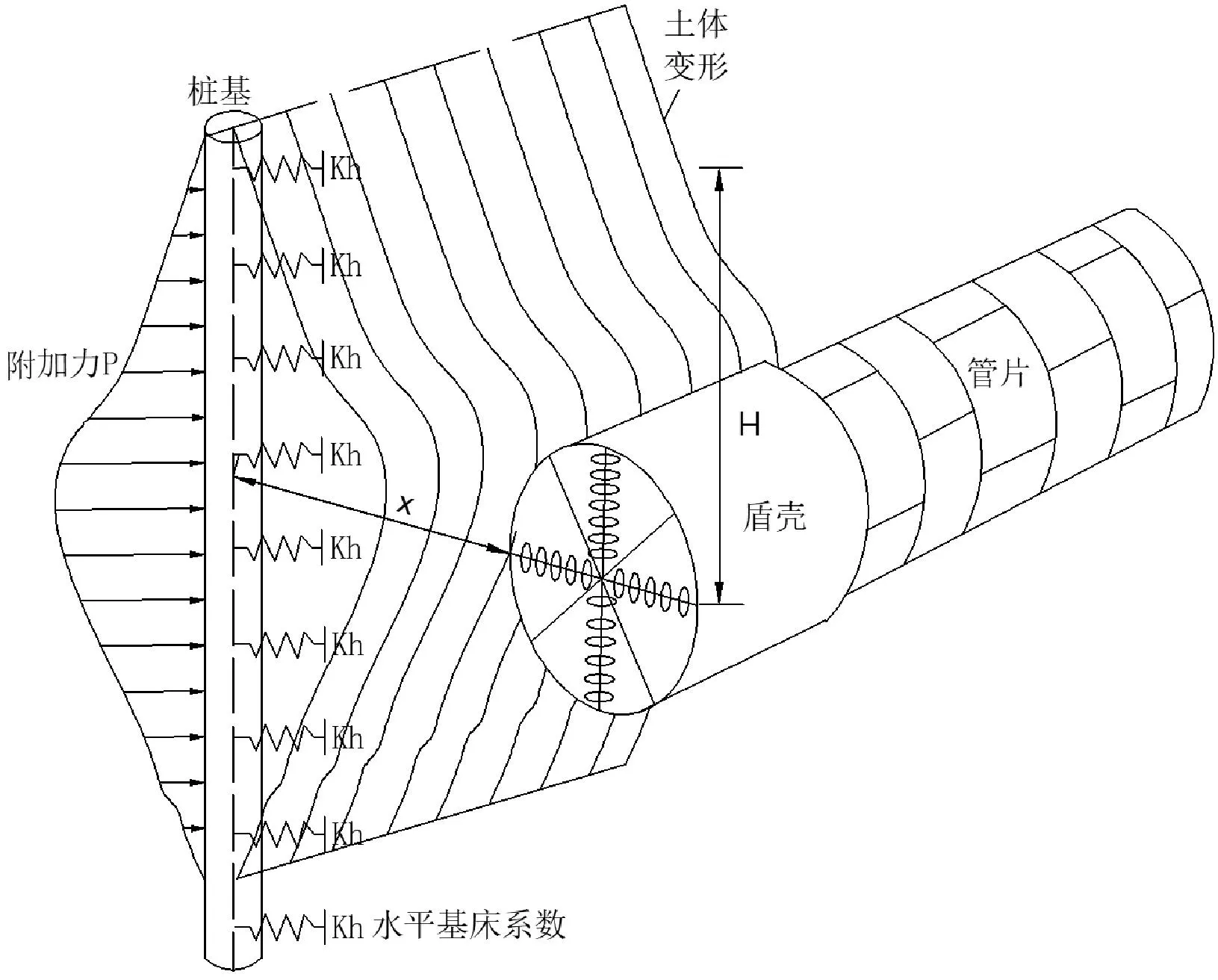
图6 盾构隧道临近桩基施工土体变形与桩基受力模型

4 桩基变形简化计算

4.1 模型的建立

在盾构机顶进推力与掌子面土压力基本保持平衡时,盾构隧道施工造成围岩土体向洞内径向变形,桩基靠近隧道侧土体位移,使得桩基两侧的土压力不平衡,遂引发桩基向隧道侧变形。参考基坑工程增量法,桩基一侧土体压力卸载即另一个土体压力的增加,荷载增加量即土体的水平位移与水平基床系数的乘积。

Tanahashi[12]提出了考虑桩土共同作用的土体水平基床系数计算经验公式:

(6)

式中:k为土体地基反力模量;P为量测位移测点设置后的围岩释放荷载;Δx为对应的量测支护外边界位移;D为桩基等效作用宽度,因此处不将圆形桩等效为矩形桩,故D等于桩基直径d;Es、μ分别为围岩的弹性模量和泊松比;EI为桩基的弹性模量。

将式(5)和式(6)结合,即可得到盾构隧道开挖导致桩基承受的附加应力P与水平基床系数kh。具体的表达式如下:

P(z)=k·Sx(x,z)·B

(7)

kh=k·B

(8)

(9)

结合式(7)、式(8)和式(9),可利用Midas civil软件建立桥墩-承台-桩基有限元模型。通过盖梁添加与支座类型相关的节点弹簧和上部结构压力、汽车水平制动力,桩基、承台添加水平基床系数(节点弹簧),模拟桥梁运营过程与盾构施工组合下桩基的最不利受力情况。

4.2 工程算例验证

(1)为了验证模型的有效性,提取了文献[13]的GEPDN边界元程序计算结果与本文简化方法进行对比。模型中假设土体为各向同性的弹性体,弹性模量24MPa,隧道开挖直径为6m,隧道中心轴线埋深20m,地层损失率为1%,桩基为C30,弹性模量为30GPa,桩基直径0.5m,桩长25m,桩基轴线距离开挖界面1.5m。对应的该弹性模量土层一般为密实土层,泊松比取0.3。采用本文方法计算,桩基等效宽度D为1.125m,相应土体损失率的径向压缩量为15mm,桩顶、桩端按自由边界条件。计算结果如图7和图8所示,可知,桩基在隧道中心轴线附加水平位移与弯矩最大。采用本文方法计算的桩身最大位移为8.55mm,GEPDN法计算的最大位移为8.10mm,误差0.36mm,占比5.5%。本文方法计算的桩身最大附加弯矩为72.7kN·m,GEPDN法计算的最大附加弯矩为58.4kN·m,相对抗弯承载能力数值误差在可接受的范围,运用于实际工程属于偏安全考虑。

图7 桩基位移对比

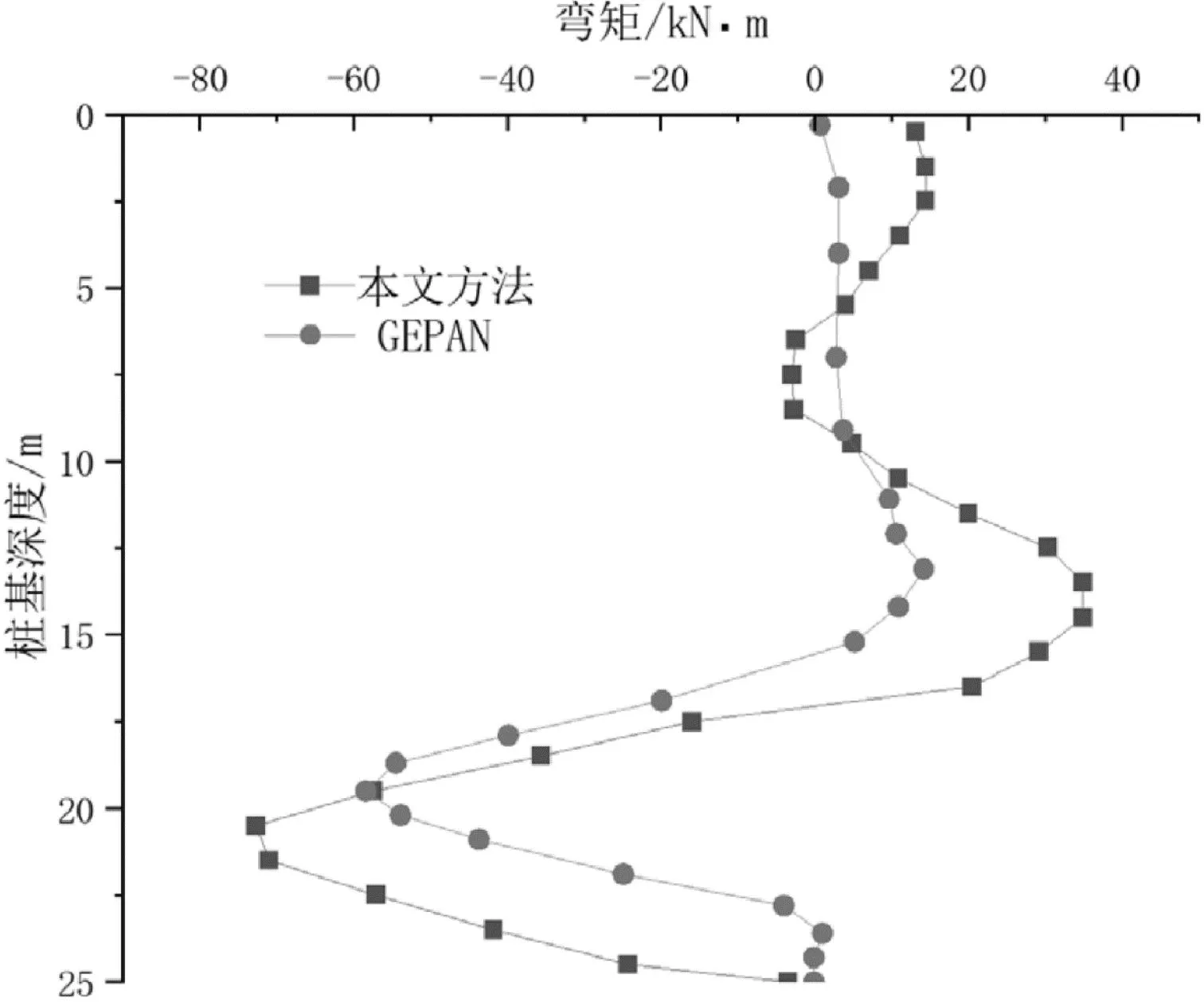
图8 桩身附加弯矩对比

图9 桩身水平位移与实测值对比

(2)Lee等[14]对实际工程中隧道施工造成的桩基水平位移进行了记录。隧道埋深15m,隧道开挖洞径8.25m,桩基轴线距离开挖界面1.575m,桩基为C30砼,弹性模量30GPa,桩基直径为1.2m,等效宽度D为1.98m,桩长28m,土体损失率约为0.5%。假定土体的弹性模量为54MPa,采用本文方法计算,相应土体损失率的径向压缩量为10.3mm。桩顶、桩端按自由边界条件,计算得到桩身最大位移为9.47mm,与实测最大值10.10mm误差6.2%,较为接近。