利用Excel实现《JJG 266-2018卧式金属罐容量》容量比较法罐容表计算
2024-01-02孙大圣
孙大圣
〔中石油海南销售有限公司 海南海口 570100〕
随着加油站油品管理工作的不断精细化以及中国石油、中国石化近年来不断推进加油站实现油品地罐交接模式,加油站卧式油罐容积表的准确性越来越重要。国家市场监督管理总局于2018年12月25日发布,2019年6月25日实施中华人民共和国国家计量检定规程《JJG 266-2018卧式金属罐容量》[1](以下简称“新规程”)。新规程中卧式罐容量测量分为容量比较法和几何测量法。
在实际油品计量工作中,涉及加油站罐容表的更新一般都是运营站点。如果采用几何测量法进行容积检测,存在以下问题:一是加油站必须停业,以及清洗油罐带来大量含油污水处理,成本较高;二是需要检测人员进入罐内检测,手动操作,环境恶劣,安全性差。相比较旧规程JJG 266-1996,2018版新规程增加了容量比较法并将其作为主要测量方法,符合实际工作需要。
1 新规程容量比较法油罐容积表计算的局限性与利用Excel表实现容量比较法罐容计算的可行性
1.1 新规程容量比较法油罐容积表计算的局限性
按照新规程,根据标称容积、注液安全高度、检尺点内竖直径和卧式罐内液位高度设定检定点数和液位高度间隔:检定点数不得少于10个;液位高度间隔应使每点之间的液位上升高度尽量一致,且不大于250 mm,不小于150 mm。这是由于如果测量点数太多,液位高度测量引起的误差较大;检定点数太少,又不能反映罐体的真实曲线特性。结合规程附录C:三次均匀B样条插值算法,这二者是一致的。也就是说,保证每点之间的液位上升高度一致是构造三次均匀B样条插值算法的基础。由于三次均匀B样条插值算法以样条插值节点等距构造的,但在实际操作中,很难做到保证每点之间的液位上升高度完全一致,总会由于这种液位上升高度不一致导致插值计算结果出现偏差。
得到所需检定点数值后,按照新规程附录C,通过求取控制点得到分段连续的均匀三次B样条曲线,再通过插值算法制作罐容表,存在以下问题:①容积比较法标罐操作很难满足液位均匀等距升高,这样会给计算结果带来偏差,如果按照工作实际构造三次非均匀样条函数,准确性更高;②计算量大,需要用到专业软件matlab、python等专业软件进行。
1.2 利用Excel实现容量比较法油罐容积表计算的可行性
Excel是日常办公软件,函数功能强大,可以利用Excel构造三次非均匀样条插值函数的三弯矩方程进行插值计算,从而弥补《JJG 266-2018卧式金属罐容量》新规程中算法方面的不足,计算简单、准确性高。
2 非均匀三次样条插值函数三弯矩方程Excel构造及计算
2.1 三弯矩法的三次样条插值函数表达式
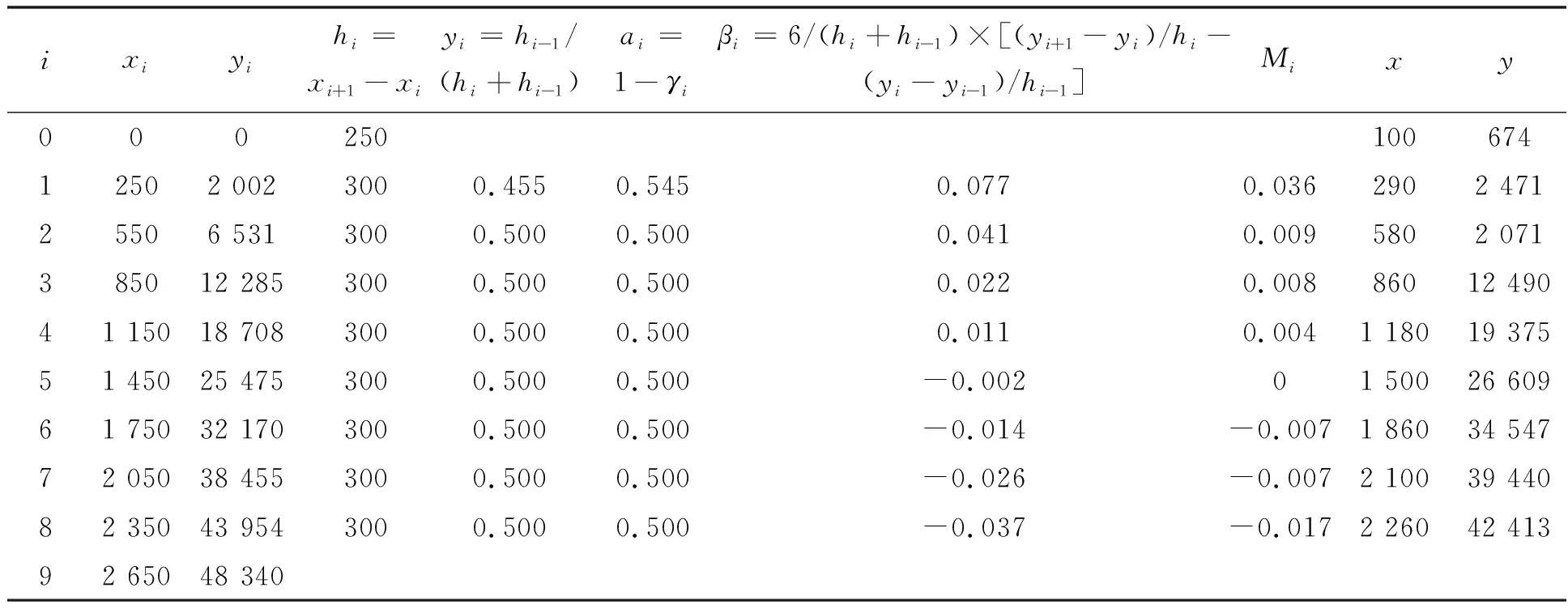
设有n+1个互异的节点x0 (1) 式中:xi-1≤x≤xi,i=1,2,…,n S″(xi)=Mi,i=0,1,2,…,n hi=xi+1-xi,i=0,1,2,…,n-1 (2) 对于样条函数的计算,关键是样条函数在各节点上的二阶微分值Mi的确定,可以根据方程组(2)构造矩阵方程γM=β进行求解。 为了便于利用Excel处理数据,一般将型值点采用列的形式布置。然后分别计算hi、γi、αi、βi等数值。 设 构造矩阵方程γM=β如下: (3) 在Excel中通过逆矩阵函数MINVERSE求得γ-1,利用公式M=γ-1β求出Mi(i=1,2,…,n-1),结合M0=Mn=0,便可以得到区间[x0,xn]任一分段[xi,xi+1]之间函数Si(x),对于给定x,首先判断其所处区间[xi,xi+1],即可利用插值函数求出对应y值。 以新规程附录C例题数据进行计算为例,给容量比较法测量数据点Q0(250 mm,2 002 L)、Q1(550 mm,6 531 L)、Q2(850 mm,12 285 L)、Q3(1 150 mm,18 708 L)、Q4(1 450 mm,25 475 L)、Q5(1 750 mm,32 170 L)、Q6(2 050 mm,38 455 L)、Q7(2 350 mm,43 954 L)、Q8(2 650 mm,48 340 L)。根据给定数据,利用Excel处理结果。 以列形式布置数据并计算hi、γi、αi、βi,Excel自动计算结果如表1。 (1)hi(i=0,1,…,n-1)计算:h0=x1-x0=250 mm,h1=x2-x1=300 mm,…,h8=x9-x8=300 mm。 (2)γi(i=1,…,n-1)计算:γ1=h0/(h0+h1)=0.455,γ2=h1/(h1+h2)=0.5,…,γ8=h8/(h7+h8)=0.5。 (3)αi(i=1,…,n-1)计算:α1=1-γ1=0.545,α2=1-γ2=0.5,…,α8=1-γ8=0.5。 (4)βi(i=1,…,n-1)计算:β1=[6/(h1+h0)]×[(y2-y1)/h1-(y1-y0)/h0]=0.077,…。 利用ai、γi构造γ系数矩阵,在Excel中用公式MINVERSE求逆矩阵γ-1,在Excel中利用矩阵公式MMULT根据M=γ-1β求解Mi(i=1,2,…,n-1),结果见表2。 表2 利用矩阵公式MMULT计算 举例说明,比如x值为100,处于0~100区间,那么此时利用已知数据在Excel中设置函数公式,其计算结果见表3。 表3 设置函数公式 (4) 按照公式模拟制作罐容表如表4,高度间隔100 mm,也可以按照高度间隔10 mm进行计算制作。容积1是指利用三弯矩方程得到的结果,容积2是利用三次均匀B样条通过型值点求控制点反求数据点得到的结果。 表4 按照公式模拟制作罐容表 从表4可以看出:①利用三次均匀B样条方法求数据点,由于通过控制点求解,在给定数据点250 mm以下没有扩展性,只能按照内插法求得数据。由于第一个基础数据高度差是250 mm(0~250 mm),不是以后基础数据均匀高度差300 mm,非均匀,所以在高度500 mm以下利用三弯矩方程计算结果与三次均匀B样条函数计算结果有较大差异,三弯矩方程结果更准确;实际应用中500 mm以下高度很少用到,结果差异可以忽略;②其余数据差异较小。 利用高度和此高度容积与前一高度容积差在Excel中作散点图,如图1,从形状可以看出能较好符合油罐上下小中间大的容积特点。 图1 高度-容积差散点图 利用Excel的函数功能能够解决油罐标罐罐容表的计算问题,无需专业软件,解决了实际操作中液位非严格等距升高带来的计算误差。在实际加油站罐容表采用此方法修正的罐容表实际应用中准确度较高,可以进一步利用该方法进行加油机(法定计量器具)修正油罐容积表。

2.2 在Excel中进行计算求解

3 利用三弯矩法三次样条插值函数实例计算油罐容积表
3.1 以列形式布置数据并计算
3.2 在Excel中利用矩阵公式MMULT计算

3.3 利用已知数据在Excel中设置函数公式
3.4 罐容表模拟制作及数据结果分析

3.5 利用高度-容积差散点图复验

4 结束语
