基于DAPF与EACO算法的无人机博弈策略
2024-01-02严航付兴建
严航,付兴建
(北京信息科技大学 自动化学院,北京 100192)
0 引言
在复杂的作战环境中,如何利用无人机实现合理的战略规划以获取最大化的收益,已成为许多研究者探索的重点问题。
在无人机的路径规划方面,文献[1]提出了一种修正人工势场的动态路径规划算法,来预测动态障碍物的位置。文献[2]在传统人工势场法的基础上,增加了一个转向力,来加快无人机的动态避障过程。文献[3]针对多无人机提出了一种有效的基于改进人工势函数的路径规划方法,通过引入旋转势场,无人机可以有效地摆脱常见的局部最小值和振荡。文献[4]将A*算法和Q-learning算法相结合,提高了无人机路径的可靠性和安全性。文献[5]提出了一种新型非线性模型预测控制方法,来预测动态障碍物的轨迹,提前规划无人机的航线。
在无人机的对抗博弈方面,文献[6]提出了一种分布式无人机群的部署方法,制定了拥塞博弈来模拟无人机群之间的交互功能。文献[7]描述了一个非线性模型预测控制器,在敌我双方追逐博弈时,预测敌机下一步的行动,为无人机提供了三个维度的规避机动决策。文献[8]建立了一个非合作攻防博弈模型,提出一种改进的量化收益方法,准确地计算包括防守方反击收益在内的博弈均衡,从而有效地预测敌方的攻击动作。文献[9]研究了N-联盟非合作博弈的纳什均衡问题,提出基于极值寻求的方法来估计成本函数的梯度,以两个无人机群在领土防御场景中的对抗分析,验证所提策略的有效性。
将无人机的路径规划和对抗博弈相结合的研究鲜有报道。本文提出一种动态人工势场法,将敌方无人机作为动态障碍物,我方要通过敌方无人机的防区,进而两者之间形成了动态对抗博弈。建立敌我双方对抗博弈模型,采用精英蚁群算法求出双方的纳什均衡策略。在纳什均衡策略中,双方无人机一旦改变策略,只会减少己方的收益。
1 问题描述
本文提出的无人机对抗博弈有两个参与者,即参与者1为我方无人机,参与者2为敌方无人机。我方的首要目标为穿越敌方无人机的防区,敌方目标为巡逻和防守所在的防区。在敌我双方对抗博弈的过程中,双方都在寻找最优的策略,使得己方收益达到最大。
在二维平面建立双方无人机的动力学模型为
(1)
式中:(x,y)为无人机的位置;v为无人机的速度;θ为无人机运动方向与x轴的夹角;ω为无人机的角速度;a为无人机的加速度。
2 动态人工势场法
人工势场法由Khatib于1986年提出。该方法思想如下:设无人机在虚拟势场中受到两个力的作用,一个是目标对其的吸引力,另一个是障碍物上的排斥力。通过两个力之间的相互作用,无人机能够避开环境中的障碍物,并到达目标位置[10]。
然而,传统人工势场法在遇到环境中存在动态障碍物或者目标为移动物体的情况时,其路径规划和避障效果不佳[11]。本文在人工势场法的基础上,加入速度斥力和速度引力因素,提出动态人工势场法(dynamic artificial potential field method,DAPF)。
(2)
(3)


图1 动态人工势场法的排斥力Fig.1 Repulsive force of dynamic artificial potential field method
则,考虑速度斥力后的排斥力公式如下:
(4)
(5)
(6)

动态人工势场法的吸引力如图2所示,其中,吸引力及其两个分量可以表示为
(7)
(8)
(9)

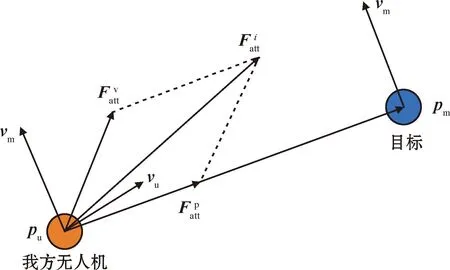
图2 动态人工势场法的吸引力Fig.2 Attraction of dynamic artificial potential field method
3 无人机对抗博弈
本文建立的无人机对抗博弈模型,主要分为博弈参与者集合、策略集、支付函数和纳什均衡策略求解四个方面。博弈参与者为动态人工势场法中介绍的敌我双方无人机。其余三方面的内容将在本节中介绍。
3.1 双方无人机的策略集
设我方有n架无人机,集合为{ξ1,ξ2,…,ξn},敌方有m架无人机,集合为{ψ1,ψ2,…,ψm}。我方对抗状态为xij(i=1,2,…,n;j=1,2,…,m),xij=1表示我方无人机选择攻击敌方,xij=0表示我方选择逃离该敌方防区。敌方对抗状态为yij(i=1,2,…,n;j=1,2,…,m),yij=1表示敌方无人机攻击我方,yij=0表示敌方无人机放弃攻击,坚守防区。
3.2 无人机对抗博弈支付函数
支付函数是博弈中参与者所获得的收益水平的函数,是每一个参与者在某种策略环境下所能获得的可能收益。支付函数不仅与每个参与者自身所选择的策略有关,还与其他参与者在同一环境下所选择的策略有关。因此,它也可以看作是所有参与者的战略或行动的函数。
设我方n架无人机价值S={s1,s2,…,si,…,sn},敌方m架无人机的价值为G={g1,g2,…,gj,…,gm},目标点归一化的综合价值为σ。
我方无人机的收益函数可表示为
(10)
式中:β为目标位置价值的权重系数;σ为目标点的综合价值;wmi为我方无人机导弹的价值;gj为第j架敌方无人机的价值;Υij为第i架我方无人机对第j架敌方无人机的攻击成功概率;gmax为我方收益的最大值。
敌方无人机收益函数为
(11)
式中:J为防区价值的权重系数;ξ为防区的综合价值;si为第i架我方无人机的价值;μij为第j架敌方无人机对第i架我方无人机的攻击成功概率;smax为敌方收益的最大值。
综上所述,敌我双方无人机的支付函数为
Hij=α1R-α2C
(12)
式中:i∈[1,κ],j∈[1,λ];α1、α2为收益权重系数,且α1+α2=1。
则双方无人机对抗博弈的支付矩阵为
(13)
式中:Hκλ表示我方无人机采用第κ策略,而敌方无人机采用第λ策略时的支付值。
3.3 无人机对抗博弈纳什均衡解
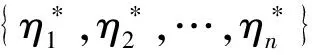
(14)
定义如下适应度函数[13]:
(15)
式中:s={η1,η2,…,ηn}为博弈的混合策略;ai∈Si为局中人i的策略集合。
根据定义1可知,当且仅当s为博弈的纳什均衡策略时,适应度函数取最小值0。
4 精英蚁群优化算法
传统蚁群算法不适用于无人机对抗博弈的纳什均衡求解问题[14]。为此,本文在蚁群算法的基础上,提出一种精英蚁群优化(elite ant colony optimization,EACO)算法。
4.1 对立学习
在EACO算法中,通过随机产生的初始种群来开始搜索最佳解。当初始种群接近最优解,则可较快找到可行解。相反地,当种群远离最优解区域时,则搜索需要较长的时间,甚至无法找到最优解。
对立学习(opposed learning)是一种机器智能的新方法。对于初始种群,对立学习可将所有初始成员位置取反,如式(16)所示:
(16)
4.2 精英成员划分
经过种群初始化后,可根据适应度函数(15),计算出蚁群中各个蚂蚁的适应度值,适应度较优的作为精英蚂蚁,其它剩余蚂蚁为普通蚂蚁,赋予相应的信息素强度。
蚁群中的普通蚂蚁根据当前的信息素强度和适应度函数计算转移概率。
(17)
式中:p(i,j)为普通蚂蚁i向精英蚂蚁j的转移概率;f(Xi)和f(Xj)分别为普通蚂蚁i和精英蚂蚁j的适应度函数值;τ(j)为精英蚂蚁j的信息素强度值;m为精英蚂蚁的数量;τ(s)和f(Xs)分别为精英蚂蚁s的信息素强度值和适应度函数值。
普通蚂蚁i根据式(17)的转移概率p(i,j)选择是否下一步向精英蚂蚁j移动。
Xi(t+1)=αXi(t)+(1-α)Xj(t)
(18)
式中:Xi(t+1)为t+1时刻普通蚂蚁i的位置;Xi(t)和Xj(t)分别为t时刻普通蚂蚁i和精英蚂蚁j的位置;α为(0,1)内产生的一个随机数。
4.3 精英变异
为了避免陷入局部最优,对精英蚂蚁进行变异操作,产生适应度函数更优的蚁群。
(19)
式中:Xj(t)和Xj(t+1)分别为精英蚂蚁j变异前和变异后的位置;β1为(0,1)内的随机数;T和Tmax分别为当前迭代次数和最大迭代次数。
完成一次进化后,更新所有蚂蚁的信息素强度和适应度值。
(20)

4.4 EACO算法具体步骤
步骤1 初始化参数,确定最大迭代次数Tmax、蚁群规模M。
步骤2 采用对立学习思想改变种群成员初始位置。
步骤3 根据适应度函数计算蚁群中每只蚂蚁的适应度值,将蚁群分为精英蚂蚁和普通蚂蚁。
步骤4 根据式(17)计算普通蚂蚁的转移概率。
步骤5 根据式(19)对精英蚂蚁进行变异操作,产生适应度函数更优的蚂蚁。
步骤6 更新所有蚂蚁的信息素强度和适应度值,重新选择精英蚂蚁和普通蚂蚁。
步骤7 当达到最大迭代次数时,停止迭代,否则返回步骤2。
4.5 EACO算法复杂度分析
优化算法的时间复杂度可以通过算法语句的循环执行次数进行衡量。在EACO算法中,重复循环次数与最大迭代次数Tmax、蚁群规模M有关。步骤1中时间复杂度为O(M);步骤2引入对立学习和步骤3划分精英蚂蚁,时间复杂度并未增加;步骤4计算转移概率和步骤5进行变异操作,时间复杂度并未增加;步骤6更新整个种群位置,复杂度为O(M×Tmax)。算法整体复杂度不高,运行效率较好。
5 仿真研究
设在复杂环境中,我方两架无人机要穿越敌方防区,到达目标区域,在飞行途中,遇到敌方两架无人机。我方两架无人机为(U1,U2),其价值分别为s1=93、s2=91;敌方两架无人机为(A3,A4),其价值分别为g1=112、g2=114;我方无人机的目标区域的综合价值σ=180,其权重系数β=0.5;敌方的防区的综合价值ξ=100,其权重系数J=0.8;双方收益权重系数为α1=0.6、α2=0.4;双方导弹的价值为wmi=wmj=10。双方无人机攻击成功概率公式如下所示:
(21)
(22)
表1为敌我双方无人机的策略集,根据式(12)和(13),求出双方无人机对抗博弈支付矩阵:
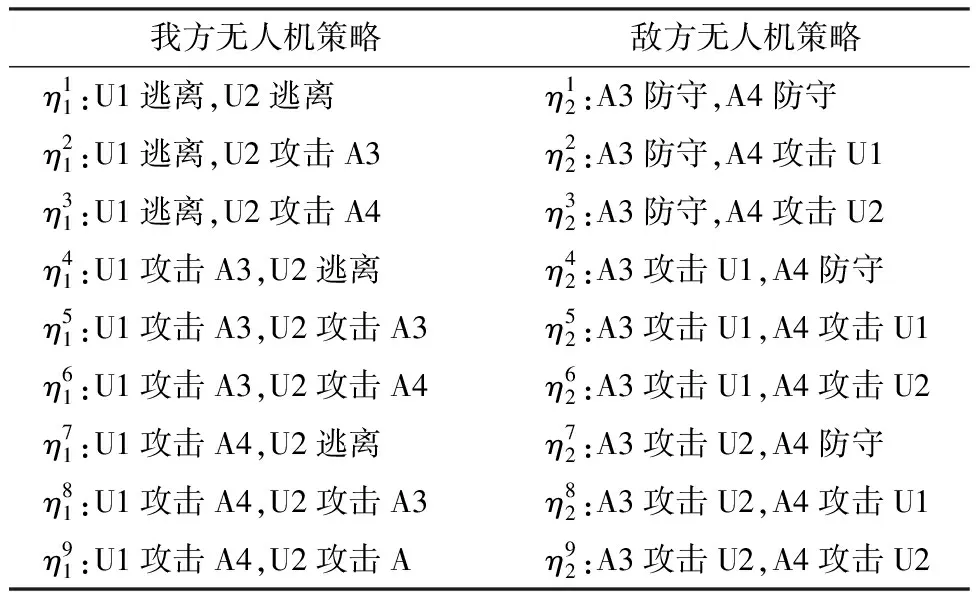
表1 敌我双方无人机策略集Table 1 UAV strategy set of both sides
采用EACO算法求解出的纳什均衡点为0.077,即,我方纳什均衡策略为U1和U2都选择逃离,敌方策略为A3攻击U1,A4攻击U1。

图3为敌我双方无人机采用动态人工势场法的对抗博弈纳什均衡策略航迹图。从图中可以看出,我方无人机U2避开敌方两架无人机,成功到达目标区域;敌方无人机A3和A4协同攻击我方无人机U1,最终在位置(-64,-8)处攻击成功。在双方无人机对抗博弈中,纳什均衡策略是双方的最优策略,妄想改变策略的一方将会损失更大。
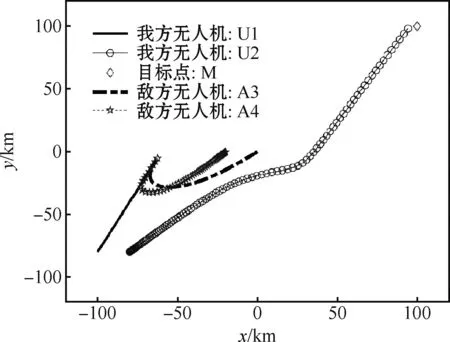
图3 动态人工势场法的纳什均衡策略Fig.3 Nash equilibrium strategy of dynamic artificial potential field method
为进一步验证本文提出的精英蚁群算法求解无人机对抗博弈纳什均衡的有效性,采用无人机对抗博弈支付矩阵Ω作为测试函数,将本文提出来的EACO算法与粒子群优化(particle swarm optimization,PSO)算法[15]、遗传算法(genetic algorithm,GA)、精英改选机制的粒子群优化(elite re-election particle swarm optimization,ERPSO)算法[16]进行对比。
算法参数设置为:种群规模为50,最大迭代次数为100;EACO算法中精英蚂蚁数量为10,信息素挥发系数λ1=0.6;参考文献[15]设置PSO算法中的个体与群体学习因子为c1=c2=1.4;GA算法中交叉与变异概率为p1=0.4、p2=0.2;参考文献[16]设置ERPSO算法中的克隆变异的个数为l1=25,重新初始化个体数l2=25,误差阈值为e=0.05。4种算法在相同仿真环境中进行50次独立实验。
表2为4种算法的性能对比结果。由表2可知,与PSO算法、GA算法和ERPSO算法相比,EACO算法所求的适应度值最优,最优适应度值为4.185 1×10-6;EACO算法平均迭代次数最少,比PSO算法减少67.85%,比GA算法减少88%,比ERPSO算法减少40%。这表明本文算法能显著降低迭代次数、提高计算精度和收敛速度,适合应用于求解无人机对抗博弈的纳什均衡问题。

表2 四种算法性能对比Table 2 Performance comparison of the four algorithms
6 结束语
本文提出了一种动态人工势场法,在人工势场法的基础上,增加了速度斥力和速度引力因素,并将该方法应用到多无人机对抗博弈策略的研究中。通过构建敌我双方支付函数,建立了双方对抗博弈模型。采用精英蚁群算法,更加高效地计算出双方的纳什均衡策略。最后,仿真结果表明了动态人工势场法和精英蚁群算法的有效性。
