基于锥形层流元件的气体微小流量测量研究
2023-12-31宋佳谢代梁徐雅黄震威刘铁军
宋佳 谢代梁 徐雅 黄震威 刘铁军
“浙江省流量计量技术研究”重点实验室·中国计量大学
气体微小流量测量在化工生产、环保、半导体生产、航空航天、真空计量学和医疗呼吸器械等领域有较大的需求[1-4]。天然气气体分析仪需要快速并高精度测量微小气体流量,气体计量在整个工业过程中占据着重要地位。层流流量计凭借响应速度快、无可动部件、量程比宽等优点,在洁净气体微小流量测量方面具有独特的优势[5-7]。
随着商品经济和市场的细分化,对天然气流量计量的精度也在逐渐提高,对气体微小流量计的需求也在逐渐增加。目前,由于我国在气体微小流量测量方面与国外尚有差距,大部分气体微小流量计主要依赖进口,实际过程中使用的流量计难以满足现实需要,因此,对气体层流流量计的研发较为迫切。
20世纪30年代, Ricardo H R和Alcock J F为了研究内燃机脉动量测量,创造性地设计出了层流流量计(当时称作黏性流量计)[8];史绍熙院士研究了用于脉动空气流的黏性空气流量计,这为后来层流流量计的开发研究奠定了基础[9]。在对气体黏度和高精度的流量测量研究中,研究人员大多采用增大毛细管长度,结合实验对各项扰动因素进行修正[10-11],从而得到更高精度的测量结果。从各项研究来看,这些装置通常加工制作难度系数较大,难以应用到流量计的研发中。在对一般层流流量计的研究中,由于毛细管束构成的流量计受进出口压损和非线性误差等各种因素的干扰[12],层流流量计固有的误差不能保证线性度,须进行标定修正,导致难以保证较高的精度。王剪等[7]提出了差分式层流流量传感技术,利用两组串联毛细管束的差压进行流量测量,缺点是需要两个高精度的差压传感器。王晴晴等[13]采用数值仿真计算,得到了单个毛细管内部的压力和流场分布,直观地展示了气体在层流元件进出口处的压力损失。
在其他的缝隙式层流流量计和片式层流流量计研发中[14-15],由于制作加工受到密闭性能不佳、装置容易变形等因素的影响,导致测量量程较为有限。新结构的层流流量计难以广泛应用在实际测量中。
本研究主要设计了一种锥形结构的层流元件,利用直接从层流流道充分发展段取压优势,尽量减小层流流量测量进出口段的压力损失,加工并制作了3种不同间隙的锥形层流元件,利用差压搭建了一套用于气体微小流量测量的实验系统,验证了基于锥形结构的层流流量传感元件用于气体流量测量方面的可行性,对比3组实验,得到了具有较高测量准确度的间隙尺寸结构。
1 层流流量计工作原理
1.1 常规层流流量计工作原理
常规层流流量计依据哈根-泊肃叶定律,基于不可压缩流体处于完全发展了的层流状态时,水平圆形管道前后两个截面的差压与流体流量成正比的关系设计而成,其计算公式见式(1)。
(1)
式中:qv为流体流量,m3/s;d为圆管(通常为毛细管)内径,即当量直径,m;Δp为上下游取压点处流体的差压,Pa;μ为流体的动力黏度,kg/(m·s);L为测压点之间距离,m。
常规层流流量计一般由整流装置、层流元件、取压装置构成,如图1所示。其中,层流元件是指放置在流道内部的毛细管束或毛细管簇,流体流经层流流量计,在毛细管内产生层流流动。在层流元件中,为了保证流体在各个毛细管中均发展为层流状态,雷诺数需要小于临界雷诺数,一般取2 000~2 300,因此,对毛细管的加工制作要求较高。
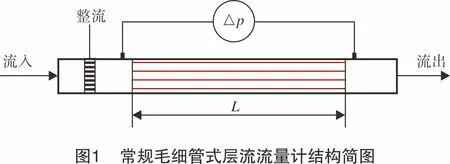
在实际应用中,由于取压装置设计在毛细管或毛细管簇入口和出口段,不可避免地引入了非线性压损,起始段可能尚未达到完全发展层流流动状态,这与哈根-泊肃叶公式理论应用条件发生偏差,导致测量误差增大,这也是常规层流流量计普遍存在的问题。
1.2 锥形层流流量计工作原理
流体在密闭管道中流动,当其流过流通面积小于管道截面积的节流装置时,流体流束会局部收缩,使得流速加快而静压力下降,从而导致所形成的环状结构入口与出口处的流束间产生差压,Δp与流经管道的气体流量成正比。锥形层流传感元件结构如图2所示,其与双锥差压流量传感元件相似。
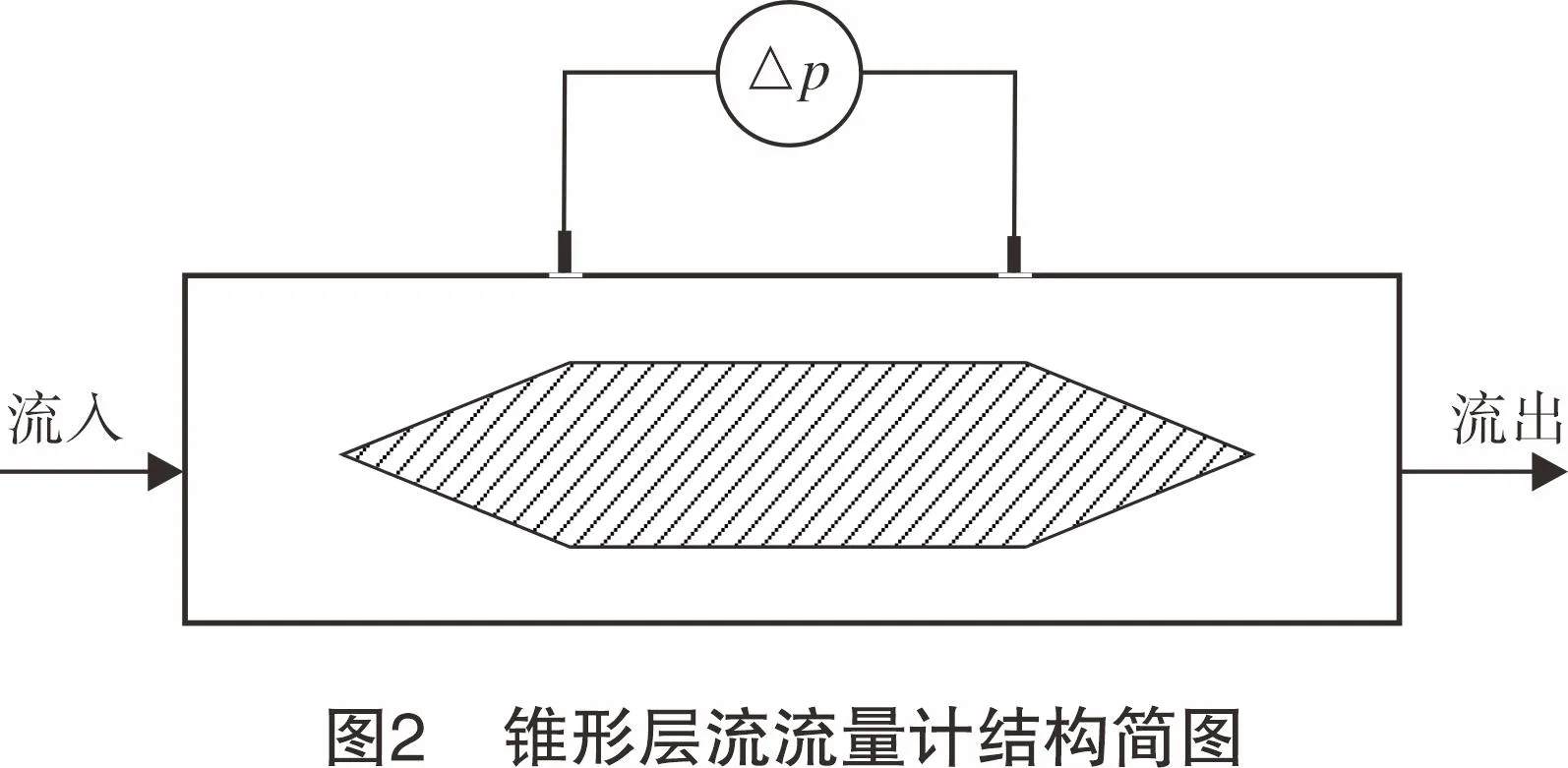
与常规圆管道层流流量计不同的是,锥形层流元件的流道为同心圆环形管道,属于非圆形管道。对于非圆截面管道内的流动,王筱庐等[16]在矩形间隙的层流流量计中将取压点设置在流道的内部,相较于毛细管流量计需要将取压点设置在流道进口与出口,这种直接接触气体介质的测量方式可以有效地避免进出口效应。
如图3所示,在圆管道内放置双锥形圆柱节流件且保持同轴心,得到同心环形管道,流体流经该管道即圆柱环形缝隙流动[17]。同心环形管道在管段内可以采取直接取压的方式。管道内壁半径为r1,中心圆柱体的半径为r2,单位为m。

流体流经环形管道,在层流定常流动过程中可以认为该流动是对称的,如图4所示。

建立坐标系,取管轴为x轴,单位为m,沿x轴方向的速度vx=vx(r),单位为m/s,如果质量力仅有重力,在管道的直径方向,压力p的梯度为0,水平方向上,p只是关于x的函数,单位为Pa,其关系式见式(2)。
(2)
式中:r为管道半径方向的长度,m。
对式(2)中的r进行两次积分,可得式(3)。
(3)
根据边界条件,r=r1和r=r2时,vx=0,确定常数C1和C2,如式(4)、式(5)所示。
(4)
(5)
将式(4)、式(5)代入式(3)可得式(6)。
(6)
对通过环形管道的流体流量进行积分,如式(7)、式(8)所示。
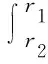
(7)
(8)
上述公式中的负号代表方向,根据锥形层流元件前后端差压Δp和两差压面间的间距L可得式(9)。
(9)
在完全充满流体的非圆截面管道中,当量直径的计算如式(10)所示。
d=2r1-2r2
(10)
2 实验测试
2.1 锥形层流发生元件实验模型
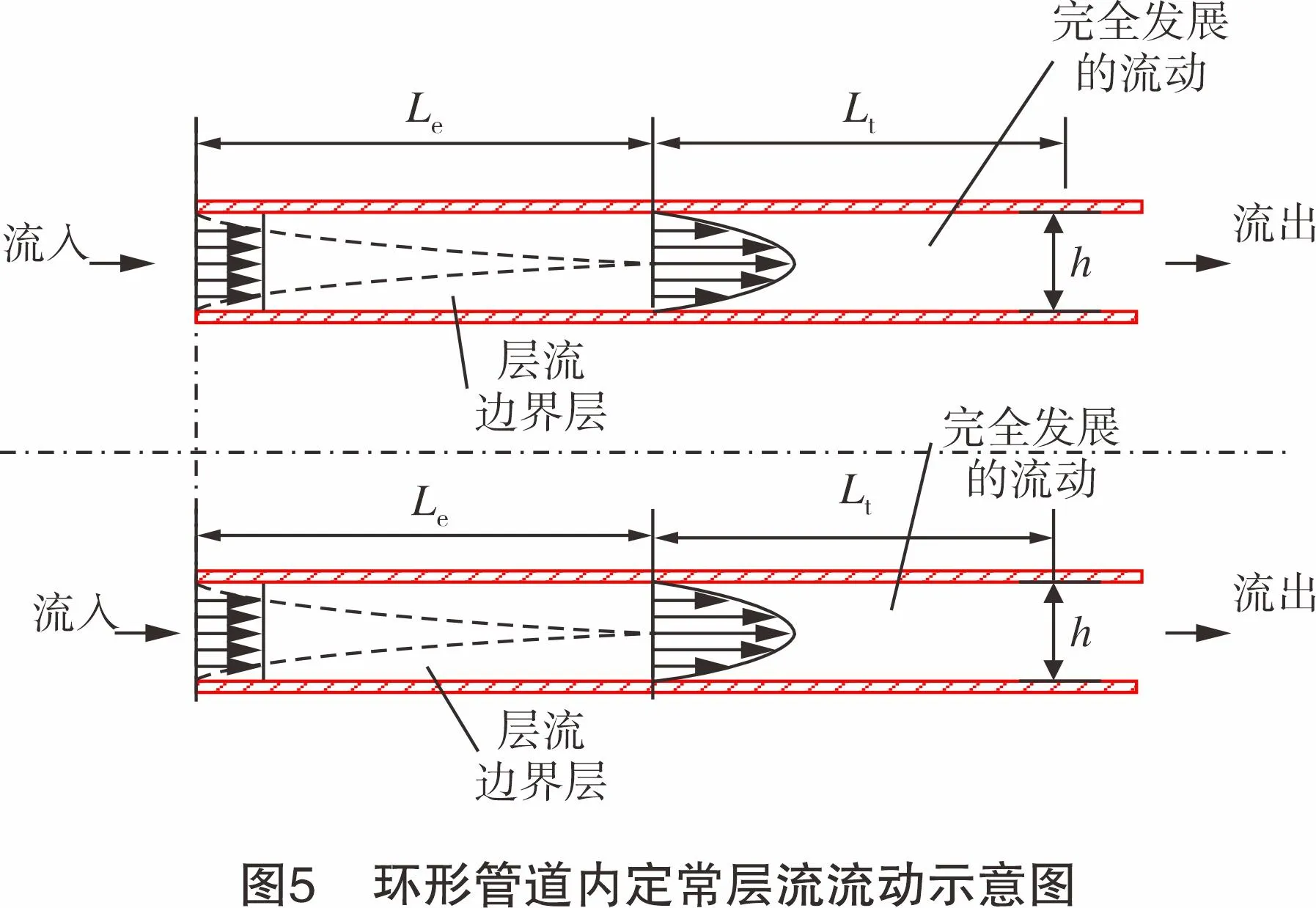
图5所示为流体介质进入间隙为h的环形管道前后的流速发展变化趋势。流体在流入环形管道后,发展段距离为Le,保证了之后流道内的流体介质发展成为可靠而稳定的层流,层流段距离为Lt。
采用分块设计,通过SolidWorks绘制出锥形层流元件的三维结构图(见图6),其前后端盖是相同的设计结构,圆锥体部分也是相同的设计结构。

管道均采用不锈钢SUS304材料,保证加工表面粗糙度小于Ra1.6,严格控制环形间隙的同轴度。采用适于空气和惰性气体测量用的橡胶密封圈进行密封连接,外筒套体管道规格为DN20 mm。为了尽量避免引入不必要的非线性误差,取压端设置在完全发展了的层流流动段L。选用3种间隙结构的圆柱体,圆柱体尺寸分别为Φ18.0、Φ18.6和Φ19.0,依次对应间隙尺寸为1.0 mm、0.7 mm和0.5 mm。最终实物图如图7所示,表1所列为不同间隙模型的尺寸参数。


表1 圆柱体尺寸参数mm参数名称数值Φ18.0圆柱体入口段长度Le7Φ18.6圆柱体入口段长度Le5Φ19.0圆柱体入口段长度Le5Φ18.0圆柱体层流充分发展段长度L10Φ18.6圆柱体层流充分发展段长度L10Φ19.0圆柱体层流充分发展段长度L10Φ18.0圆柱体结构出口段长度LO3Φ18.6圆柱体结构出口段长度LO5Φ19.0圆柱体结构出口段长度LO5
锥形传感元件中前锥面的作用是稳定气体流入并将迎面而来的气流均匀地分布到环形管道内,后锥面设计可以有效地避免当流体流出流道时由于突扩而带来的旋涡。有研究学者在研究层流流量计时选用了圆球面的层流元件构造并且取得了较好的实验结果[17]。结合前人经验,采用30°锥角进行实验。中间圆柱体外径尺寸见表2。

表2 中间圆柱体尺寸参数mm参数名称参数数值圆柱体外径2r218.0圆柱体外径2r218.6圆柱体外径2r219.0
2.2 实验测试系统
搭建了利用锥形层流元件适用于微小气体流量测试的实验系统(见图8),包含了音速喷嘴气体流量标准装置,差压仪表,压力测量仪表以及温度测量仪。实验介质选用洁净空气,气体流量标准装置可以同时测量温度、压力、湿度传感器信号,在标准状况下,其量程范围为0.016~6.500 m3/h,装置的整体不确定度为±0.3%(k=2)。差压计选用康斯特公司的ConST221智能数字差压表,量程为-2.5~2.5 kPa,准确度等级为0.02级。气体绝对压力的测量仪选用康斯特公司的ConST211数字压力表,其测量量程为0~160 kPa,准确度等级为0.05级。温度测量仪测温范围为0~50 ℃,最小分度值为0.1 ℃。

2.3 实验结果及分析
根据质量守恒定律,流经锥形层流元件与空气流量标准装置前后的气体质量流量相等。实验中的气体流量标准装置给出了工作状态下的气体体积流量,由于空气分子之间存在间隔,且空气分子之间不断运动,气体在各个状态下的体积流量会发生变化,必须用质量流量进行量化。因此,需要得到工作状态下空气的密度,其计算公式见式(11)。
(11)
式中:ρ1为空气的密度,kg/m3;ρn为标况下空气的密度,kg/m3;p1为空气的工作压力,Pa;pn为标况下的空气压力,Pa;T1为工作温度,K;Tn为标况温度,K。
流经气体标准装置的气体质量流量等于该时刻下气体的体积流量与该工况下密度的乘积,其计算公式见式(12)。
qs=ρ1qv
(12)
式中:qs为气体质量流量,kg/h;qv为气体体积流量,m3/h。
计算流过锥形层流元件装置的流量时,应考虑到气体压缩性的影响。首先计算工作状况下气体的体积流量,然后根据绝对压力和温度进行密度修正,其计算公式见式(13)。
(13)
式中:q1为流经锥形层流元件层流充分发展段的体积流量,m3/h。
环境因素中的温度对结果准确性的影响最大[18],空气在锥形层流元件内的动力黏度由流经空气的温度确定[19],其计算公式见式(14)。
μ=(17.23+0.048t)/1 000 000
(14)
式中:t为温度,℃。
锥形层流元件充分发展段空气的密度计算公式如式(15)所示:
(15)
式中:ρ2为层流元件内的空气在工作状况下的密度,kg/m3;p2为ConST211绝对压力表测量得到的压力,Pa;T2为气体流量标准装置的温度示数,K。
流经锥形层流元件的气体质量流量为该时刻下气体的体积流量与该工况下气体密度的乘积,其计算公式见式(16)。
q*=q1ρ2
(16)
式中:q*为工作状况下流过层流发生装置的气体质量流量,kg/h。
由于受锥形层流元件内部结构的特殊性等不确定因素的影响,需要在实验中确定各结构的锥形层流元件的系数K,K由式(17)确定。
(17)
式中:m为测量总次数,本实验中测量总次数为30次。
最终工况质量流量由式(18)确定。
q=Kq*
(18)
式中:q为最终工况锥形元件的质量流量,kg/h。
依次将3款间隙分别为1.0 mm、0.7 mm和0.5 mm的锥形层流元件进行实验,并且对10个流量点进行3次测量。部分测量结果分别如表3、表4、表5所列,标定间隙为1.0 mm、0.7 mm和0.5 mm的锥形层流元件特定系数K1、K2、K3分别为0.996、1.292、1.852。表3中第5列为测量结果的相对误差,其计算公式如式(19)所示。

表3 环形流道间隙为1.0 mm装置的测量数据qs/(kg·h-1)Δp/Paq*/(kg·h-1)q/(kg·h-1)δ/%0.015 11.20.014 80.014 8-1.830.023 71.90.023 50.023 4-1.300.038 03.10.038 40.038 20.690.076 86.20.076 70.076 4-0.420.464 737.60.465 10.463 4-0.260.748 861.10.755 50.752 70.531.134 492.81.146 01.141 80.661.598 9130.91.614 41.608 60.601.882 8154.91.908 51.901 61.002.347 2192.52.367 82.359 20.51

表4 环形流道间隙为0.7 mm装置的测量数据qs/(kg·h-1)Δp/Paq*/(kg·h-1)q/(kg·h-1)δ/%0.015 12.70.011 60.015 0-0.420.023 74.30.018 50.023 90.720.038 06.80.029 30.037 8-0.410.076 813.90.059 80.077 30.660.464 783.90.360 80.466 00.290.748 9135.60.582 60.752 50.491.134 7205.20.880 41.137 20.221.599 5288.61.235 81.596 2-0.201.883 6339.41.451 31.874 5-0.482.348 3424.21.809 22.336 8-0.49

表5 环形流道间隙为0.5 mm装置的测量数据qs/(kg·h-1)Δp/Paq*/(kg·h-1)q/(kg·h-1)δ/%0.015 05.10.008 00.014 8-0.730.023 68.00.012 60.023 3-1.120.037 712.90.020 30.037 6-0.300.076 226.00.040 90.075 7-0.630.460 9160.80.252 40.467 51.430.742 8259.50.406 90.753 61.451.125 5391.80.613 41.136 00.941.586 2558.70.860 21.593 20.441.867 9658.61.010 61.871 80.212.328 8810.61.237 52.292 0-1.58
(19)
式中:δ为相对误差,%。
利用质量守恒定律,将工作状况下的体积流量转换成质量流量进行计算,减少因气体压缩性带来的影响。
根据表3可知,在基于间隙为1.0 mm装置的实验中,量程范围超过150倍,除去前两个小流量点,整个系统的测量误差保持在±1%以内。计算可得整个流量范围的雷诺数最大不超过1 300,小于临界雷诺数2 000,证实整个流动处于层流流动状态。
两个小流量点处差压表的读数均小于2 Pa,受限于差压表下量程范围,如选用分度值更小的差压表测量,测量结果会更好。在大流量点2.347 2 kg/h处,差压值为192 Pa左右,计算得到的雷诺数小于1 300,说明流量测量范围还可以更大。
为了更好地展示流量与差压之间的关系,绘制了流量与差压的关系图,如图9所示。在整个流量测量实验中,流量和差压保持良好的线性关系,展示出了锥形层流元件应用于微小流量测量在线性度方面的优势。

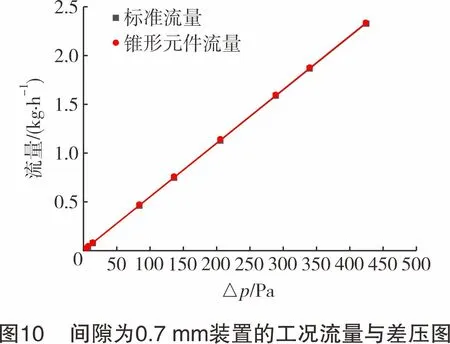
由表4可知,在基于间隙为0.7 mm装置的实验中,整个流量测量系统的测量误差保持在±0.8%以内,测量范围超过150倍。在测量最大流量点2.348 1 kg/h处,差压值为424.3 Pa左右,计算该流量点处的雷诺数为1 198,说明流量测量范围还可以扩大。
对比间隙为1.0 mm装置的空气流量测量数据,在相同的流量点处,差压测得值变大,测量误差变小。
图10所示为流量与差压的关系图。从图10可以看出,在整个气体流量测量范围内,差压与流量始终保持良好的线性关系。
间隙为0.5 mm装置的实验结果见表5。整个流量测量系统的测量误差保持在±1.6%以内,测量范围超过150倍,流量为2.328 8 kg/h时雷诺数达到最大值1 199,小于临界雷诺数2 000,保证了在整个测量过程环形流道的流动状态始终为层流流动。首个小流量点qs=0.015 0 kg/h时,误差在0.7%左右,相较于间隙为1.0 mm和0.7 mm的锥形层流元件测量数据,最小流量点处的差压明显增大5.1 Pa左右,分别是间隙为1.0 mm和间隙为0.7 mm的锥形层流元件差压值4.3倍和1.9倍,最大测量误差没有出现在最大流量点,也没有出现在最小流量点,而是出现在中间流量点处。相较于前两种间隙结构,最大流量点处的差压也增大到810 Pa左右。最大流量点处的雷诺数仍然小于临界雷诺数,说明整个量程比将远大于150。
将表5中流经0.5 mm间隙的锥形元件的流量与差压数据进行绘图(见图11),从整体上看,流量与差压保持高度的线性关系。

按照流量点从小到大依次编号,将基于3种间隙结构的锥形层流元件流量测量系统各30次实验的相对误差进行比较,对比展示见图12。3种间隙结构的锥形层流元件在空气微小流量测量实验中均表现良好,基于间隙为1.0 mm、0.7 mm、0.5 mm的锥形层流元件在超过150倍的流量测量范围内测量误差均小于1.8%,保持在±2%以内。以间隙为0.7 mm的锥形层流元件测量系统为最佳,测量误差均小于0.8%,保持在±1%以内,测量误差比较稳定;其次是以间隙0.5 mm的锥形层流元件测量系统,测量误差保持在±1.6%以内。
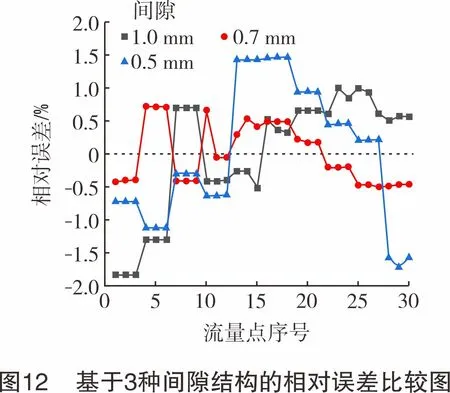
国际上著名的用于微小流量测量的层流流量计品牌Fluke和Alicat,分析其设计的层流流量计产品误差,测量误差指标一般在±1%左右[20]。在本次实验中,基于0.7 mm间隙的锥形层流元件测量偏差在±1%左右。在超过150的量程比范围内,基于3种间隙装置的层流元件实验中,流量与差压保持着良好的线性关系。可以认为,基于锥形层流元件的微小流量测量研究对促进层流流量计的发展,以及将其用于天然气微小流量测量具有重要意义。
3 结论
本研究提出了基于锥形层流元件的气体微小流量测量技术,介绍了锥形层流元件流量传感技术的工作原理,分析了环形管道内层流流动理论,加工并组装了3套不同间隙结构的锥形层流元件,与气体流量标准装置配合设计了微小流量测量装置实验。主要结论如下:
(1) 在微小流量范围为0.015 0~2.348 1 kg/h进行实验,间隙为1.0 mm、0.7 mm和0.5 mm的锥形层流元件系统的最大测量误差为分别为-1.83%、0.66%、-1.58%,3组测量误差均保持在±2%的范围内。其中,基于间隙为0.7 mm的锥形层流元件测量系统效果最佳,测量误差在±0.8%以内,小于±1%。
(2) 在利用基于3组间隙结构的锥形层流元件测量气体流量时,其工况压力与流量均保持良好的线性关系。基于流量测量的相似性原理,放大流量和升高压力后,经过实验验证,层流流量元件有望用于天然气流量测量。
