LNG薄膜罐主容器的轻量化设计
2023-12-31狄骏皓王琪郭旭丁徐强杨鹏飞
狄骏皓 王琪, 郭旭 丁徐强 杨鹏飞
1.江苏科技大学机械工程学院 2.南通理工学院汽车工程学院 3.张家港中集圣达因工程有限公司
LNG是由天然气冷冻至-162 ℃液化而成,其主要成分为甲烷,燃烧后产生的排放物对环境污染极小,能够有效降低NOx、SO2、CO2和PM的排放,是全球最为清洁的化石能源[1]。2022年,我国天然气消费总量为3 663×108m3,占全国能源消耗总量的8.9%,远低于全球天然气消耗占全球能源消耗的24.1%,预计到2040年我国天然气消费量将会达到6 155×108m3[2]。未来LNG在我国的使用量将会显著提升,存在巨大的消费市场。随着全国最大的盐城“绿能港”储罐升顶成功,意味着我国的天然气储罐正在向超大型化、现代化方向发展。LNG储罐的开发研究对于开发和扩大LNG市场也具有较大的促进作用,能有效缓解国内其他化石能源的消耗压力。
国内外诸多学者从理论方面对储罐的结构优化进行了研究。谢剑等[3]利用ANSYS软件进行有限元分析并采用控制变量法对穹顶所受载荷进行多次校核计算,通过分析实验数据得出影响穹顶应力和位移的因素主要有外罐直径、穹顶曲率半径和穹顶厚度等;黄文健[4]对穹顶进行了全面的受力分析,使用牛顿迭代法基本原理及JAVA程序求解穹顶最低预应力来保证穹顶安全性;季冰乙[5]通过创建储罐有限元模型,深入分析内罐泄漏工况下,预应力系统对罐壁的内力分布、罐壁配筋和罐壁液密性影响。得出横向预应力和竖向预应力对罐壁影响的大小关系,从而对罐壁进行结构优化;Santhosh等[6]在储罐屈曲约束状态下对统一模型进行了拓扑优化并找出了最佳的穹顶形状,并且相比原有模型在质量上减少了6%,实现了储罐的轻量化设计。
本研究以储罐直径、穹顶曲率半径和罐壁厚度为变量,对储罐结构的轻量化设计进行了优化。通过建立薄膜罐数学模型和目标函数对主容器进行受力分析,并利用ANSYS软件进行参数化设计和应力分析,利用粒子群算法求取最优解,并对最终结果进行了试验验证。
1 储罐结构设计
本文研究的对象为立式圆筒平底钢质的LNG薄膜罐,薄膜罐的结构简图如图1所示[7]。其由1个薄膜的钢质主容器、绝热层以及1个混凝土罐共同组成。混凝土罐外部为工作平台以及钢质走道,钢质穹顶下方为铝质吊顶,穹顶部分和吊顶部分用吊杆和吊顶加强筋连接,吊顶下方是玻璃纤维棉制的吊顶绝热层。薄膜罐相较于其他储罐而言,能将储罐的绝缘性和气密性作用明确分离,且罐容没有极限。对LNG薄膜罐的穹顶结构优化研究更符合未来储罐大型化、轻量化的发展趋势。
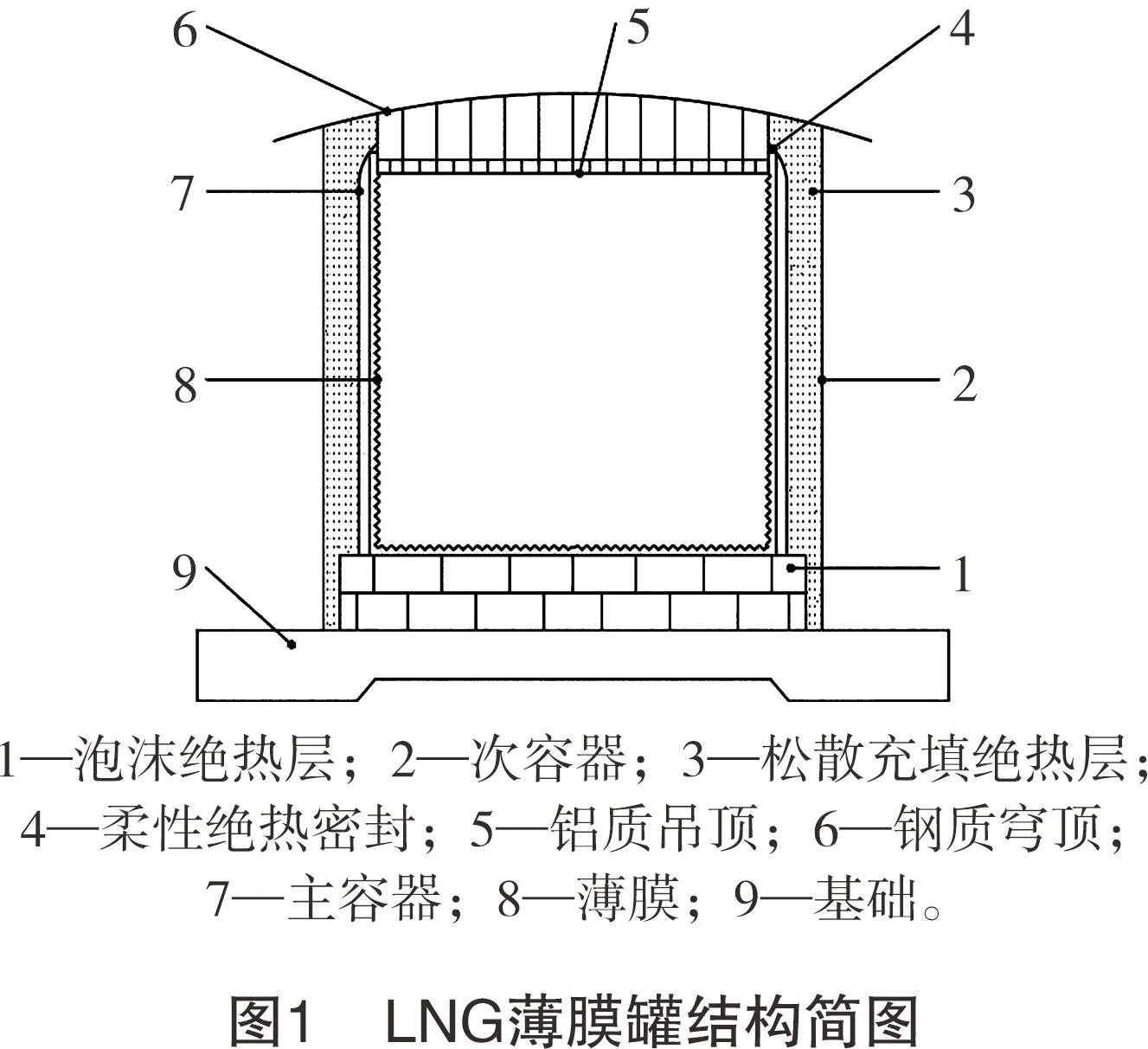
LNG薄膜罐的主容器为立式圆筒钢质结构,本研究中的储罐基于相关标准和规范设计。其各部分基本几何参数见表1。
初始穹顶设计厚度的初始值按式(1)计算:
(1)
式中:S0为初始穹顶设计厚度,m;pd为主容器内压,MPa;Di为穹顶内直径,m;Sts为材料设计许用应力,MPa;JE为焊接接头系数,无量纲;C为钢板厚度负偏差,mm。初始设计穹顶材料厚度为6.5 mm,此时穹顶弧度为82°。
根据GB 50341-2014《立式圆筒形钢制焊接油罐设计规范》中的定设计点法,初始罐壁设计厚度如表2所列。
2 优化穹顶数学模型
2.1 建立数学模型

(2)
式中:h为矢高(BD长度),m;A为穹顶面积,m2;R为曲率半径,m。
2.2 目标函数
穹顶的结构尺寸设计取决于储罐半径、穹顶的曲率半径以及穹顶厚度。因此,在储罐半径固定的前提下,选取最优的曲率半径R和钢板厚度S,以寻求最轻穹顶质量。S和R的数量关系如式(3)所示,取S的最小值。
(3)
式中:S为钢板厚度,m;p1为储罐设计内压,取0.025 MPa;φ为穹顶焊接接头系数,取0.35;[σ]t为设计温度下许用应力,取160 MPa;C1D为顶板钢板负偏差,取0.3 mm;C2D为顶板腐蚀裕量,取0.3 mm。
在储罐直径和高度确定的情况下寻求罐顶的最优厚度以及罐壁的最优厚度,从而得到最轻罐壁质量[9]。目标函数M如式(4)所示。
(4)
式中:M为主容器的最优质量,kg;ρ为镍钢材料密度,取7.20×103kg/m3;δ为罐壁厚度,m。
2.3 约束函数
根据储罐设计标准GB 50341-2014规定,储罐穹顶的曲率半径应为储罐直径的0.8~1.2倍。且储罐穹顶设计需要满足式(5)所示的应力要求。
(5)
式中:D为储罐直径,为35 m;σmax(i)为穹顶表面的最大应力,MPa;[σi]为镍钢的材料许用应力,MPa;σmax(k)为罐顶与罐壁连接处的最大应力,MPa。
3 有限元分析参数化设计
3.1 主容器受力分析
在满罐状态下,储罐罐壁主要受内罐液体静压载荷以及地震作用,储罐穹顶受到的力主要是受穹顶本身结构的质量产生的自重载荷、铝质吊顶以及吊顶拉杆等产生的附加静载、内载荷、雪载荷、风载荷以及地震载荷等[10-12]。
3.1.1穹顶外载荷
穹顶及吊顶各部件质量如表3所列。

表3 穹顶附件各部分质量及材料kg部件名称质量材料铝吊顶板1 180AL5083吊顶拉杆20 020S30408吊顶加强筋34 200S30408吊顶绝热层16 800玻璃纤维棉
穹顶的面载荷集度指的是将穹顶所受的力以均布载荷的方式添加到整个穹顶上,可反映穹顶所受静力的情况。穹顶所受均布载荷为1 200 N/m2。穹顶受外载荷的面载荷集度T按式(6)计算。
(6)
式中:T为面载荷集度,N/m2;g为重力加速度,取9.8 m/s2。
3.1.2风载荷
对于储罐风载荷的计算参考GB 55001-2021《工程结构通用规范》,储罐穹顶风载荷标准值可按式(7)计算。
(7)
式中:ωk为穹顶风载荷标准值,N。
3.1.3地震作用
对于地震作用的受力分析方法,采用振型分解反应谱法对其进行分析,确定地震反应谱后进行储罐的模型简化并初步模态分析得出最大加速度,接着计算不同状态下需要施加的加速度大小,利用ANSYS软件对满罐状态下的储罐进行竖向运行基准地震作用(operating basis earthquake, OBE)分析。满罐状态下的OBE最大响应分析结果如表4所列。
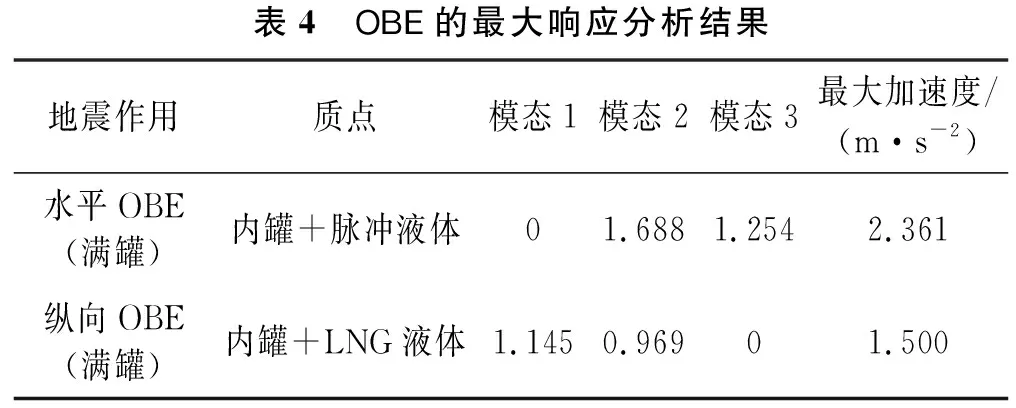
表4 OBE的最大响应分析结果地震作用质点模态1模态2模态3最大加速度/(m·s-2)水平OBE(满罐)内罐+脉冲液体01.6881.2542.361纵向OBE(满罐)内罐+LNG液体1.1450.96901.500
根据GB 55001-2021选取储罐罐顶受外载荷、内载荷、风载荷作用下的最不利载荷组合工况进行应力分析,穹顶所受载荷效应组合值S如式(8)所示。
T=Gk+γQ1φC1Q1k+γQ2φC2Q2k
(8)
式中:T为穹顶载荷效应组合值,MPa;Gk为永久载荷的标准值,N;Q1k为风载荷的标准值,N;Q2k为地震作用下的可变载荷值,N;γ为可变载荷的分项系数,无量纲;φ为可变载荷的载荷的组合值系数,无量纲;Q1为风载荷作用的标准值,MPa;Q2为地震作用的标准值,MPa;C1为风载荷作用的可变值,MPa;C2为地震作用的可变值,MPa。
3.1.4罐壁静液体静压载荷
不同液位高度下LNG液体对主容器侧壁的压力大小不同,两者函数关系如式(9)所示。
p=ρg(20.80-Z)
(9)
式中:p为主容器侧壁的压力,kPa;Z为罐壁沿高度方向值,m;ρ为LNG液体密度,kg/m3;g为重力加速度,N/kg。
3.2 ANSYS参数化设置
在DesignModeler模块中绘制二维草图尺寸以及绘制平面时对穹顶高度和顶板厚度进行参数化设置,罐壁厚度按表2中数据进行建模,且为减少在使用ANSYS软件仿真时的计算时间和计算量,将储罐的三维模型简化成整体的1/4进行分析[13],在DM中进行对称处理。为防止在后续穹顶优化研究过程中网格划分对实验结果造成的影响,需要先对穹顶应力最大处进行网格无关性检验[14],根据表5网格无关性检验数据可知,当网格数超过1 336个时,最大等效应力之间的误差在2%以内,因此,本研究选用2 783个网格单元进行分析。

表5 网格无关性检验数据网格数量/个最大等效应力/MPa19849.321 33657.362 78358.485 41658.2211 86457.7430 05059.10
在Workbench模块中将静态结构分析、模态响应谱分析以及风载荷的分析3种案例进行SRSS组合分析。接着生成dxdb文件并提取薄膜罐的最大应力σmax。
在对罐壁进行优化时,随机给定一组设计变量作为罐壁厚度,此变量数据放置于可供ANSYS软件调用的文件中,此时粒子坐标为(δ集,R),δ集=(δ1,……δ8),R=17.5为定量。在ANSYS中进行循环运算,选取满足应力条件的5组数据绘制成表6。
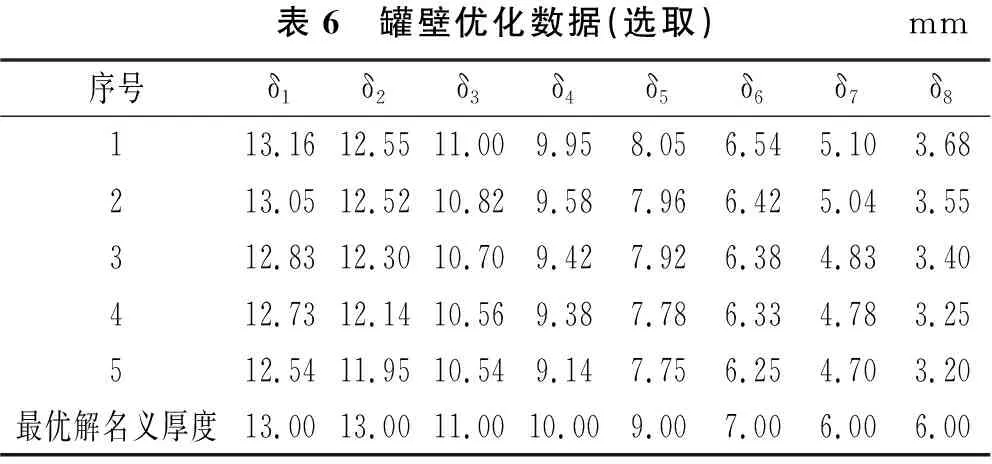
表6 罐壁优化数据(选取)mm序号δ1δ2δ3δ4δ5δ6δ7δ8113.1612.5511.009.958.056.545.103.68213.0512.5210.829.587.966.425.043.55312.8312.3010.709.427.926.384.833.40412.7312.1410.569.387.786.334.783.25512.5411.9510.549.147.756.254.703.20最优解名义厚度13.0013.0011.0010.009.007.006.006.00
4 优化方法设计
4.1 粒子群算法设计
粒子群算法属于进化算法的一种[15],是受鸟群觅食集群活动的规律性启发, 鸟群在搜寻食物的过程中通过相互信息交换,从而判断自身是否处于最佳位置。此算法可在限定范围内共享群体和个体的运动信息,使复杂无序问题变得有序,并通过适应度来确定解的优劣性,最终通过多次迭代而获得最优解,具有易实现、精度高和收敛快等优点[16]。对于确定罐体直径的储罐穹顶的优化问题,以穹顶曲率半径及板材厚度为变量,以面载荷集度为目标函数,使用粒子群算法能快速有效地求得最优解。
使用粒子群算法进行优化时,利用无质量粒子进行运算,该粒子只具有速度和位置两个属性,在进行穹顶结构优化时粒子位置坐标相对应于穹顶的板材厚度和曲率半径这两个自变量。设计算法运算流程如下[17]:
(1) 参数设置。设置算法的惯性权重ω=0.9,粒子维度Q=2,个体学习因子c1=2、群体学习因子c2=2,粒子群规模n=20,迭代次数K=20,最大迭代步数Smax=2。
搜索边界Plimit=(xmin,xmax)如式(10)所示:
(10)
式中:S为板材厚度,mm;R为穹顶曲率径,mm。最大速度vmax=(Simax,Rimax)(v为粒子速度,mm/s;Simax为第i个粒子的最大板材厚度,mm;Rimax为第i个粒子的最大曲率半径,mm)。
(2) 初始化。初始化种群中每个粒子的位置xi=(6,28)及速度vi。
(3) 适应度计算。计算每个粒子的适应度值f,适应度函数为穹顶最大应力值。根据粒子初始位置以曲率半径和板材厚度为依据建立参数化模型并进行ANSYS有限元分析计算,利用ANSYS生成dxdb文件,提取最大等效应力值σmax。
(4) 数据记录。记录并更新最佳曲率半径和罐壁材料厚度组合即粒子的最佳位置xbest,种群最佳尺寸组合Pg及其适应度值fbest。
(5) 更新粒子位置与速度如式(11)所示:
(11)
式中:rand1()、rand2()为0~1之间的随机数;z为随机粒子,无量纲。
(6) 迭代规则。返回第3步进行迭代,当迭代后利用MATLAB读取生成的dxdb文件后提取的最大应力值若大于120 MPa时,则跳过步骤(4)直接找出最佳尺寸组合(Sbest,Rbest)和群体最优解。
(7) 当达到最大迭代次数时停止迭代。输出全局最优解和穹顶最小等效应力σmin,此时粒子的位置则为全局最优尺寸组合。
在对罐壁进行优化时,程序随机给定一组设计变量作为罐壁厚度,此变量数据放置于可供ANSYS软件调用的文件中,此时粒子坐标为(δ集,R),δ集=(δ1,……δ8),R=17.5为定量。
根据上述算法步骤设计,绘制如图3所示的粒子群算法流程图。
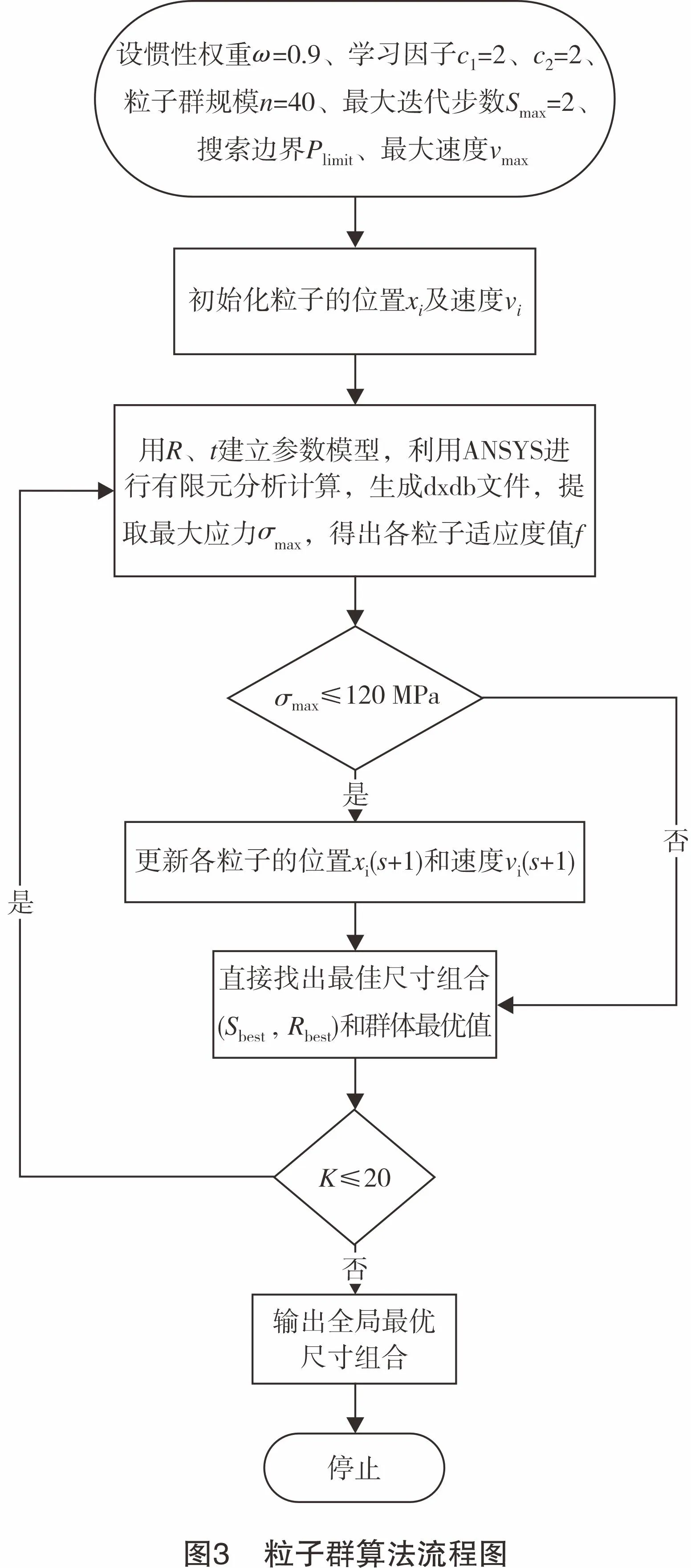
4.2 罐顶优化结果
根据4.1节所示算法步骤并利用MATLAB设计算法程序[18],得出目标函数关于穹顶曲率半径及板材厚度的三维图像曲线,算法迭代完成后得到粒子的最优位置及最优解[19-20]。
经过多次优化,最终得到穹顶曲率半径为28 000 mm、穹顶板材厚度均为6 mm时为最优解且满足设计要求。连续5次优化结果对比如表7所列。
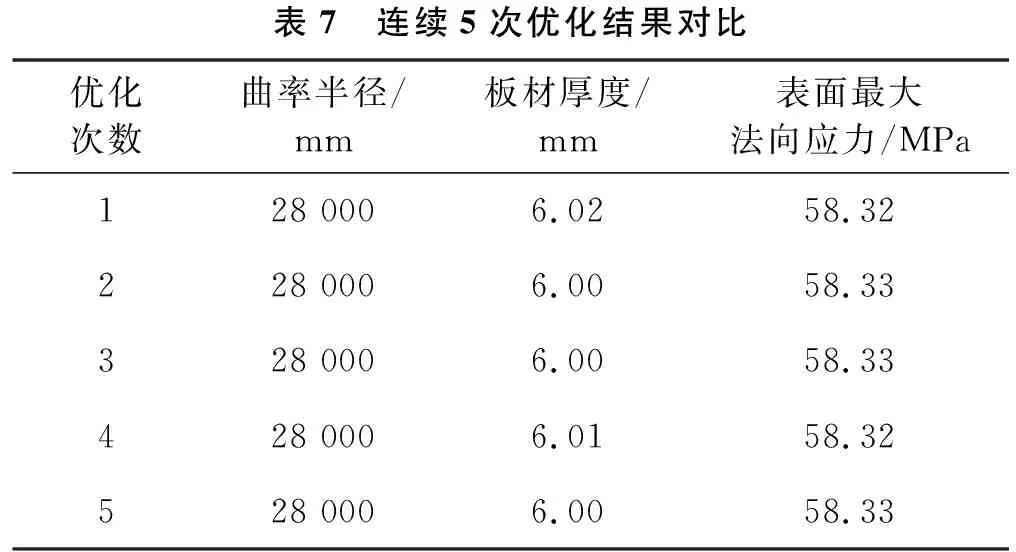
表7 连续5次优化结果对比优化次数曲率半径/mm板材厚度/mm表面最大法向应力/MPa128 0006.0258.32228 0006.0058.33328 0006.0058.33428 0006.0158.32528 0006.0058.33
5 优化后结果
5.1 优化前后结果对比
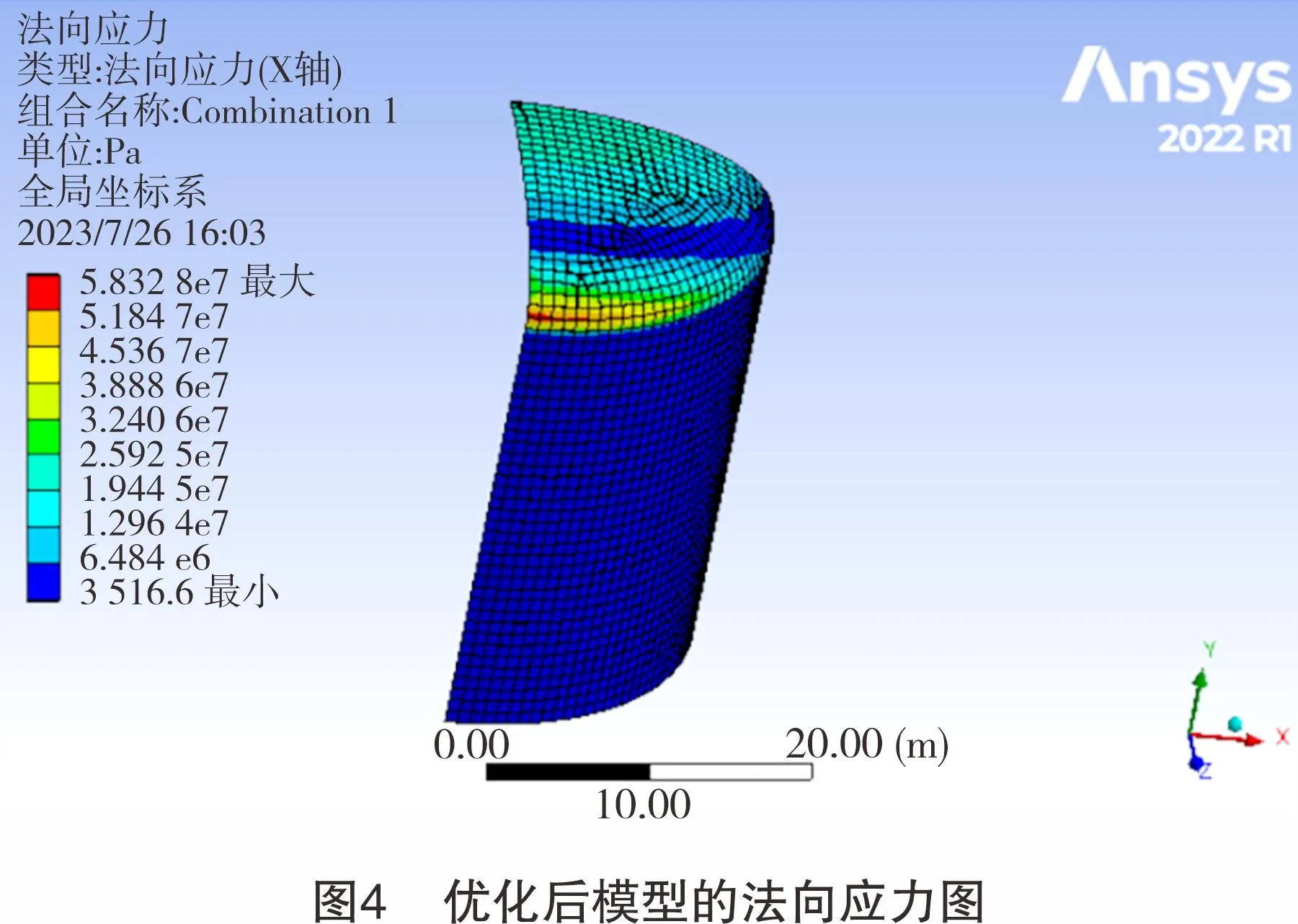
罐壁部分优化后实际所需厚度发生了改变,罐底部分名义厚度减小了1 mm。罐顶部分优化后的穹顶材料厚度减小了0.5 mm,此时的穹顶半径为28 000 mm,弧度由初始的82°变为78°,此时穹顶的质量减轻了103 t,实现了罐体的轻量化目标。优化前后结果对比如表8所列,优化后的模型法向应力分析图如图4所示,满足应力要求。

表8 优化前后结果对比优化前后穹顶半径/mm穹顶厚度/mm穹顶弧度/(°)罐底最厚部分/mm优化前30 0906.58213.16优化后28 0006.07812.54
5.2 优化后实验结果
基于上文对罐顶结构的优化分析,得出此罐穹顶的最优曲率半径为储罐直径的0.8倍,穹顶厚度为6 mm。此时主容器表面所受的最大应力满足要求,对优化后结果进行气压实验。气压试验中,环境温度为20 ℃,操作介质温度为20 ℃的干燥空气,使用精度等级为1.6级、量程为0~40 kPa的压力表对储罐进行耐压试验,试验压力为31.25 kPa,保压时间为60 min,储罐无渗漏,无可见异常变形,无异常响声。进行严密性试验时,试验压力为25 kPa,保压时间为24 h,储罐无渗漏,无明显异响。符合设计要求。优化后结果被应用于中集圣达因山东临沂两万方薄膜罐项目。
6 结论
本文以LNG薄膜罐为研究对象,为得到主容器最轻质量,对储罐结构进行了优化设计。设计了适合的粒子群算法并利用ANSYS和MATLAB软件进行分析优化。所完成的主要工作如下:
(1) 根据相关标准对相关参数进行初步设计。利用ANSYS对LNG储罐罐顶进行受力分析,根据薄膜罐的几何结构即其中的数量关系得出了目标函数,并确定了影响因子。
(2) 利用参数化、模块化设置解决工程结构应力分析问题。分析过程中在ANSYS不同模块中进行参数化设置并通过多组数据对罐壁厚度进行了优化。
(3) 将工程问题和算法相结合。设计合适的粒子群算法,并利用MATLAB进行编程和ANSYS提取其计算过程中的最大等效应力,得到了罐顶最优曲率半径以及罐顶和罐壁的最优材料厚度。
(4) 对优化后的薄膜罐主容器进行气压试验检验,优化后的薄膜罐实现了轻量化的目标,且更具经济性。
