基于动态时间规整的制丝批次间差异评价方法

吴 悦

（红云红河烟草（集团）有限责任公司新疆卷烟厂，乌鲁木齐 830026）

烟草原料在同一加工线上的不同批次之间的质量表现并不完全相同，这种批次间的差异性主要由原料差异、工艺参数变化和操作差异等因素造成[1]。尽管不同批次烟丝使用的原料属于同一配方，但由于原料来源、产地、品种、等级和贮存时间等因素的差异，原料本身会存在一定的非均一性，导致理化性状和组分特征存在差异。在连续生产过程中，工艺参数难以保持绝对不变，设备状态、环境温湿度等变化都可能导致工艺条件存在微小变化。另外，由于操作人员的经验和技能差异也会影响操作的标准性，从而导致加工结果存在差异[2]。

评价不同批次烟丝加工的差异性，对于保证卷烟产品内在品质的稳定性具有重要意义[3]，这种评价可以找出影响烟丝和卷烟质量的原料、工艺等关键因素[4]，据此优化工艺参数的设定，缩小批次间差异，提高产品质量的一致性[5]。此外，对烟丝加工批次间差异性的评价和控制，也有助于控制质量波动，保证卷烟产品的稳定性[6]。在卷烟生产企业，越来越多的技术人员开始关注到智能数据分析技术在产品质量方面的应用[7]。

智能数据分析在金融、安全、医疗、能源和工业[8]等多个领域的决策中发挥着重要作用，在工业生产制造中，异常检测是智能数据分析的重要组成部分[9]，其任务是揭示给定数据集中的异常行为。目前有几种常用方法，包括统计模型、聚类、神经网络、决策树、基于最近邻的方法和行为模式匹配等对异常检测产生了比较大的作用。但是在应用上有一个很大的挑战，那就是随着生产制造过程的进行，每天都有大量数据产生，但可用的标注数据往往有限，尤其是神经网络、深度学习等技术在小数据集上的表现不佳，因此有必要将研究方向转向其他方法以应对不同场景的挑战。

卷烟生产制造产生的大量数据属时间序列数据，大部分时间序列异常检测算法都基于时间序列之间的距离进行决策，然而在处理不断变化的时间序列时，一般的距离度量方法，如Lp-norm 范数或欧氏距离（Euclidean Distance，ED），难以实现，主要是因为实际生产中2 个时间序列长度并不一致，以及微小的时间扭曲也会导致较大的度量惩罚。为解决这个问题，Lines 等[9]提出的弹性相似度度量（Elastic Similarity Measure，ESM）显示出能够解决这类问题的潜力，在时间序列窗口内采用灵活的对齐模式，从而显著提高计算出的相似度的准确性。

在过去的几十年中，动态时间规整（Dynamic Time Warping，DTW）作为ESM 的代表之一，在语音识别、签名验证、手势识别、时间序列分类和相似度测量等领域[10]因为在灵活的点对点对齐方面表现出色而得到广泛应用。由于DTW 的二次复杂度较高，使得其难以用于在线处理，目前计算优化进行了广泛研究并取得了令人鼓舞的进展[11]，使得目前的边缘计算设备能够快速且在线取得相应结果。

在卷烟制丝的实际生产实践中，大部分企业采用以过程能力指数（Process Capability Index，CPK）和西格玛水平为代表的统计过程控制（SPC）对产品质量进行评价[12]，然而，首先这2 个指标的计算基于正态分布的假设，但实际数据分布可能并非总是正态分布，导致它们的准确性受到影响。其次，统计量的度量要求生产过程在一定时间范围内保持稳定，但生产过程不可避免会因各种因素波动，无法满足使统计过程控制有效的正态性假设[13]。最后，虽然CPK 指数关注过程能力和规格限的匹配程度，但可能忽略了过程的偏移情况，即使CPK 值较高，实际产品质量也可能受到影响[14]。因此，虽然这些度量在理论上可以提供有关生产过程能力的重要信息，但在实践中，可能需要额外的工具和技术来应对实际生产过程的复杂性和动态性。最值得关注的一点是，由于料头和料尾过程难以满足正态分布假设，绝大多数包含设备、产品变化的关键信息被截取、剔除，只关注料中的稳态数据，导致数据利用率不高、关键变化信息缺失。

本文的主要贡献是设计一种有效的批次间差异评价方法，能够克服传统比较不同速度下的相似过程，不需要满足正态分布假设，能够将生产各个阶段的信息提取并评价，并且具有直观的可视化结果，具有进一步结合烟草行业熟悉的SPC 相关技术进一步拓展的可能性。

1 相关工作

1.1 异常检测

异常检测的主要任务在于识别给定数据集中的异常或正常数据点或模式[15]，在机器学习领域可以根据可用数据的性质划分为有监督、无监督或半监督的问题：如果标记的数据集包含正常和异常样本，可以建立有监督的分类任务，利用最近邻、决策树或神经网络等方法解决；如果数据无标签，那么只能采用无监督的聚类方法，使用无监督或半监督方法则训练单类模型，如支持向量机或SOM 网络等，在正常数据样本上进行训练，如果新的样本超过正常样本一定阈值，那么则认为新的样本存在异常。

局部离群因子[16]是一个基于最近邻方法的示例，它对每个局部结构而不是每个数据点进行评分，并将得分最高的局部结构报告为异常局部结构，其中离群值和离群值组很容易根据结构的特征进行划分，与传统算法相比，该方法能够更有效地检测异常值，特别是对于具有非球形聚类的数据集。

隔离森林[17]作为另一种检测方法及其扩展，在机器监测数据和高维数据[18]等异常检测领域取得了成功应用。该方法试图通过随机选择任何可用特征，然后在所选特征的最大值和最小值之间随机设置一个阈值来隔离观察样本。通过递归分割，可以生成一棵树结构，而异常值通常从根节点到叶节点的路径更短。这种方法的计算复杂度为O（nlogn），其中n是对象的数量。

近年来，使用神经网络进行异常检测的兴趣逐渐增加。基于神经网络的检测在不同领域发挥着重要作用，如使用无监督学习进行压水反应堆的异常检测[19]，以及使用图神经网络进行工业物联网的异常检测[20]。然而，基于神经网络的异常检测主要存在着黑盒原理的问题——很难由专家验证检测过程，而且神经网络需要大量数据进行训练。

在任何异常检测系统中，都隐含了一般性正常的状态，在半监督的情况下，基于正常状态的模型，而检测的任务是找到未见过样本与正常模型的匹配程度，匹配程度越高，样本为异常的可能性越低。然而，在很多情况下，使用简单的相似度度量，如ED，很难将正常行为与观察到的时间序列匹配，这可能导致高假阳性检测。而DTW 作为一种可行的解决方案[21-22]，则通过提供所需的弹性，实现了最佳的对齐，从而降低了假阳性，并能同时检测异常。

对于监测应用来说，基于状态的异常检测模型从理论上说应该非常有效，这些应用的输入数据是从相同的数据分布中生成的，并且在平稳区间内变化很小；但是从实际应用的角度来看，满足给定的数据分布几乎是不可能的，因为实际生产环境各种传感器不可避免地存在漂移和随机干扰。判断这种渐进变化是临时的（即真正地异常）还是（生产环境本身的影响）是一项非常具有挑战性的工作。

1.2 动态时间规整（DTW）

动态时间规整（Dynamic Time Warping，DTW）[23]是一种用于测量2 个时间序列之间相似度的方法。它能够处理非线性的时间扭曲，因此在多个数据挖掘任务中可以进行灵活的对齐，在很多领域，DTW 都表现出了出色的性能，对于2 个长度不等的时间序列，即

式中:Xm是一个长度为m的向量，其元素{x1，x2，…，xm}是序列X的样本值，类似地，Yn是一个长度为n的向量，其元素{y1，y2，…，yn}是序列Y的样本值。这2 个向量可以代表任何时间序列数据，例如音频信号、传感器读数、股票价格等。为了寻找这2 个时间序列之间的相似度，本方法通过寻找2 个时间序列之间的最小累积点对点对齐来实现，在现实世界中，2 个时间序列的长度不可能完全一致（例如Xm和Yn中m和n大多数情况下并不相等），换句话说，如果可以找到一种方式来“对齐”这2 个序列，使得它们的总体距离最小，那么这个总体距离就可以作为2 个时间序列之间距离的评价方式，在DTW 中这种“对齐”的方式被称为一个“路径”。

一个路径p是一个长度为k的序列{p1，p2，…，pk}，其中每个pi＝（i，j）表示一个对齐的点对。为了保证这个路径的唯一性，这个路径必须满足以下的约束。

1）边界条件：

公式（2）的意义在于路径p必须从2 个序列的开始处开始，到2 个序列的结束处结束。

2）连续性：对于所有的i，pi+1-pi＝（1，0），（0，1）或者（1，1）。也就是说，路径不能跳过任何一个点。

3）单调性：对于所有的i，pi+1≥pi。也就是说，路径不能回溯。

在以上定义的基础上，路径p定义使得路径上的点对的距离总和最小。这个距离总和可以定义为

其中d（pi）是点（x，y）对pi的距离，通常可以定义为欧氏距离

这个问题可以通过动态规划来求解。首先定义一个距离矩阵D，其中D（i，j）表示序列X的前i个点和序列Y的前j个点的最小距离。那么D（n，m）就是想要求的最小距离。这个矩阵可以通过以下的递推公式来计算

式中：d（i，j）＝（xi-yj）2是点（i，j）的距离。公式（5）的含义是，对于每一个点对（i，j），都可以通过在（i-1，j），（i，j-1）或者（i-1，j-1）中选择一个距离最小的点对来达到。

这个递推公式的初值可以定义为

公式（6）（7）（8）分别表示X的前i个点和第一个点的最小距离，以及X的第一个点和Y的前j个点的最小距离。

如图1 所示，2 个随机时间序列x，y，通过递推公式，就可以从（1，1）开始，依次计算出矩阵D 的所有元素，然后，通过回溯这个矩阵来找到最佳的路径。具体的回溯过程是从（n，m）开始，依次在（i-1，j）（i，j-1）和（i-1，j-1）中选择一个距离最小的点对，直到回到（1，1）。

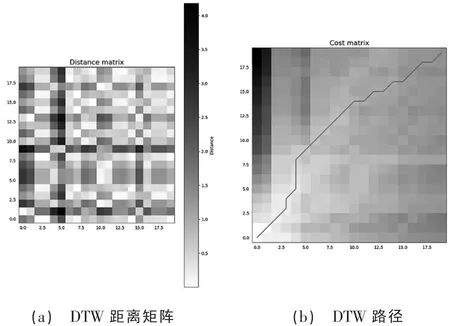
图1 2 个当变量时间序列x，y 的DTW 路径和距离矩阵

图1 （a）为DTW 距离矩阵，每个像素的颜色代表了相应的距离，颜色的深浅通常用来表示距离的大小，深色表示大的距离，可以帮助我们直观地看到2 个序列之间的相似性和差异性。如果2 个序列非常相似，那么Distance Matrix 的可视化图中将会有一条明亮的对角线。图1（b）为DTW 路径，如果2 个序列相似的部分越多，那么这些部分在可视化图中将会越接近对角线。

2 方法提出

2.1 推广到多变量的情形

在复杂的数据环境中，单变量分析方法常常无法充分利用所有的数据信息，这限制了其在实际问题中的应用。特别是在处理时间序列数据时，每个时间点可能包含多个观测值，因此需要将分析方法拓展到多变量情况。虽然动态时间扭曲（DTW）方法在单变量情况下可以有效地计算2 个时间序列之间的最优匹配，但在多变量情况下，每个时间点都包含多个观测值，这就要求计算多个时间序列之间的最优匹配，以便更准确地反映数据的特性。因此，考虑多变量情况是实现更准确分析和更全面的数据利用的必然选择，这对于提高分析方法的强大性和适应性具有重要意义。

为了说明如何将动态时间扭曲（DTW）推广到多变量情景，考虑一个批次生产过程（batch process），如公式（9）所示，矩阵X 大小为（m×P），表示该生产批次数据有m个采样点以及P个传感器；同理，公式（10）中，需要对比的批次大小为（n×P），表示该生产批次数据有n个采样点以及P个传感器，在每个批次中，有m或n个采样点，每个采样点都通过P个传感器进行多维度观测，生成了一个P维向量。例如，xi（P）表示第i个采样点通过第P个传感器得到的观测值。矩阵X 和Y 分别表示2 个批次的所有观测值，其中每行代表一个采样点的所有观测值，每列代表在所有采样点上的一个特定传感器的观测值。

对于某一时刻t0，所对应的采样点分别为i和j，一般情况下考虑生产中的各种因素i≠j，那么对于该时刻，行向量xi与yj之间的距离可以由公式（11）表示

该距离为余弦距离，其几何含义为空间中2 个向量的夹角。其中，Xi，k和Yj，k分别是向量xi和yj在k 维上的元素；两向量的点乘（即在每一维上的元素相乘然后求和），表示了向量xi和在各维度上的共享信息；而分母分别是2 个向量的欧几里得长度，用于对各自的向量进行归一化。因此，公式（11）定义了矩阵X 和某一时刻在空间中的夹角，如果2 个向量越相似，余弦相似度越接近1；如果2 个向量越不相似，夹角越大，余弦相似度越接近-1。用1 减去余弦相似度，得到的就是余弦距离，其值范围在0~2 之间，数值越小，表示2 个向量越相似。

具体算法如算法1 所示。

2.2 基于DTW 的制丝批次间差异评价方法

除了统计过程控制（SPC）相关技术以外，在实践中还经常使用“黄金批次”或“优质批次”指代在一系列生产批次中，质量、性能或产量最优的一个批次，其过程数据也常作为基准，用来与其他批次进行比较，或者用来优化生产过程，但是并没有一个统一的方法论，直观与朴素的实践是各个过程变量都要控制在一定范围内波动。

之前讨论了如何使用DTW 计算2 个多维时间序列之间的相似度，在此基础上，在处理制丝生产过程数据时，可以选择一个性能最优的“黄金批次”，并用它的时间序列数据作为参考，计算其他批次与“黄金批次”之间的DTW 距离。

如果某一个批次与“黄金批次”的DTW 距离较小，则说明这个批次的时间序列与“黄金批次”在时间结构上更加相似，该批次的生产过程更为接近最优；反之，如果DTW 距离较大，则说明这个批次在生产过程上存在明显差异，需要进行优化。

之前使用公式（11）以及算法1，可以得到“黄金批次”与被评价批次之间的距离，重复该过程，可以计算黄金批次与其他所有批次的DTW 距离DTW1，DTW2，…DTWk。

为了合理的设置阈值，

公式（12）中，5%prercentile表示5%分位数，用来确定总体批次与“黄金批次”的DTW 距离下界；同理公式（13）使用95%分位数确定总体批次与“黄金批次”的DTW 距离上界。之后，可以通过视觉化展示每个批次的DTWi及阈值范围，直观地评价不同批次与黄金批次的相似程度，从而分析每个批次的生产过程与黄金批次存在的差异，指导生产过程优化。

3 应用于松散回潮工序的实验

3.1 松散回潮工序描述

松散回潮是烟草加工过程中的关键工序之一，其主要目的是调节烟叶的湿度和温度，为后续工序的加工提供理想的湿度状态的烟叶原料。

一般来说松散回潮工序可以分为烟叶的预处理和松散回潮两部分，预处理包括烟叶的开包、分切、真空回潮等，将原料烟叶进行预处理；松散回潮是在松散回潮机内完成的工序。松散回潮机主要由钢制框架、不锈钢外壳、旋转环、支承轮、传动装置、喂料斗、出料斗、升降系统和热风加热系统等组成。烟叶进入滚筒后，控制系统会根据烟叶的流量和在线水分探测结果计算出所需的加水量，然后在适当的时间将计算所得的加水量准确喷淋在烟叶上完成湿化过程。滚筒内部分为增湿区和水分平衡区，增湿区主要通过烟叶表面对水分的吸附作用来增加湿度，水分平衡区则利用渗透作用使烟叶内外的水分含量达到平衡。为了提供理想的加热湿化环境，热风加热系统会提供适量的热风，与蒸汽混合后吹入滚筒内部，通过控制热风与蒸汽的比例可以精确调节空气湿度，实现烟叶理想的加热增湿效果。此外，还可以通过调节滚筒的转速和倾斜角度来控制烟叶在滚筒内的停留时间，以达到所需的增湿效果。出料端安装有在线水分检测仪，可以实时检测烟叶的湿度，并将信号反馈给控制系统，完成湿度的闭环控制。

3.2 松散回潮工序数据描述

松散回潮工序的数据采集主要集中在烟叶流量、水分、温度和加水量等方面，这些数据的监测对于评估湿化效果和反馈控制至关重要。

本次测试采用的实验数据为某卷烟厂正常生产时所采集的离线数据，在松散回潮机的进料端安装有电子皮带秤，可以实时检测并控制进入滚筒的烟叶流量，确保流量稳定；同时在进出料端分别安装在线水分检测仪，监测烟叶的水分含量，根据两端水分数据计算并控制加水量。为了记录系统加水量与实际加水量的对比，还需要检测和记录实际的加水量值。出料端的温度探头能够监测烟叶出料的温度，与水分数据配合判断加热湿化的效果。另外，压缩空气压力、给水系统压力、滚筒转速和倾角等数据也需要被检测和控制，这些数据与加水量和湿化效果密切相关。压缩空气压力能确保气动元件工作正常，给水系统压力影响加水量的稳定，滚筒转速和倾角决定了烟叶在筒内的停留时间，从而影响湿化效果。表1 为松散回潮工序主要变量描述，通过对表1 中的多种数据的监控收集和分析，可以实现烟叶湿化过程的闭环控制，确保烟叶得到均匀而适量的湿化处理，为后续工序提供理想状态的烟叶原料。

表1 松散回潮工序主要变量描述

读取某卷烟厂x 牌号2022 年1 月—2022 年6 月所生产的100 个批次的松散回潮设备生产数据，整理为三维过程变量数据X（100×18×Ki），其中选取第1 批次作为参考批次，其余99 个批次作为被评价批次，由于原料重量、采集结束点等不同，100 个批次的采样数Ki均不相同。

3.3 实验结果

为了说明本文所提出方法的有效性，先采用参考批次自身进行比较和评价，图2 为DTW 距离矩阵与动态规整路径，X（纵坐标）为参考批次，Y（横坐标）为被评价批次，在DTW 路径上为一条斜率为1 的直线，图像中矩阵颜色的深浅代表DTW 路径的长度，DTW 路径矩阵中各点均同步对齐，总距离为0。

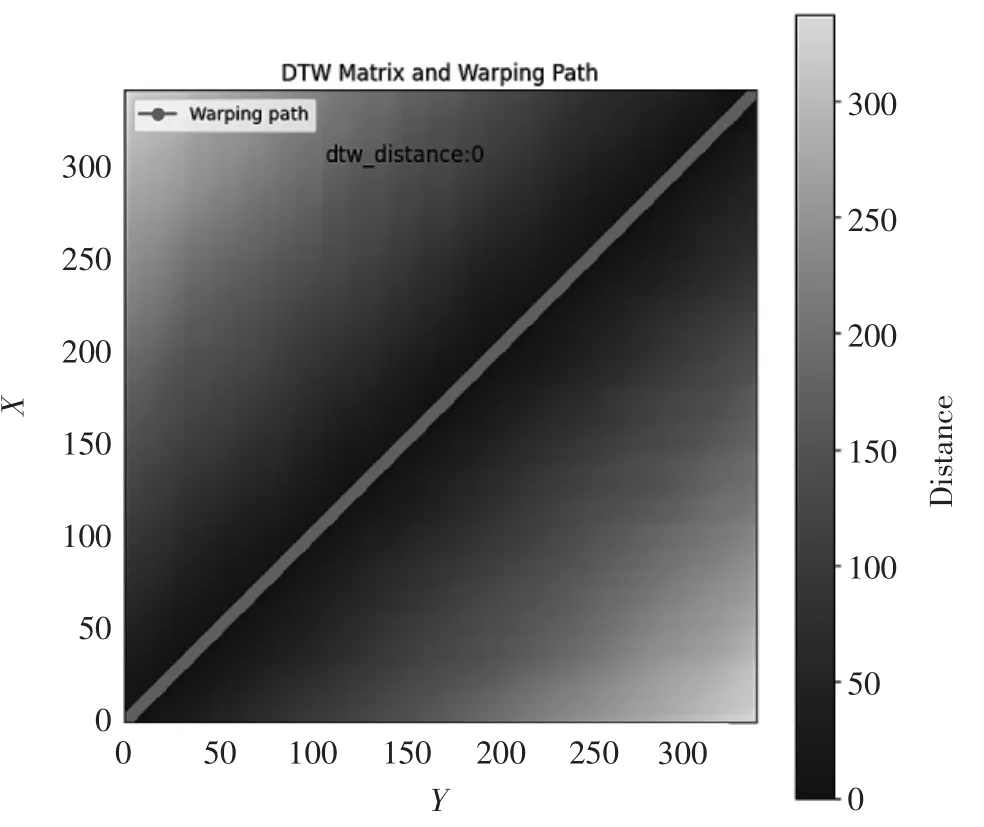
图2 参考批次自身进行差异性评价的结果

图3 为随机选取了一个批次采用本文所提出的方法进行差异性评价，由于参考批次X其采样点为300个，被评价批次Y为321 个，其DTW 路径矩阵大小为（300，321），因此被评价批次Y在第300 个采样点之后的21 个点，均以映射的方式扭曲至参考批次X的最后一个点，与其计算余弦距离。从图3 可以看出，在被评价批次生产开始初期，约25 个点，其距离与参考批次迅速加大，在生产中期保持平稳，以线性关系缓慢增加，之后在生产结束阶段将距离进一步加大，可以判断出该批次与参考批次的主要差异在于料头和料尾的控制过程中，可能出现生产结束前清线不彻底导致批次采样时间增加的问题。

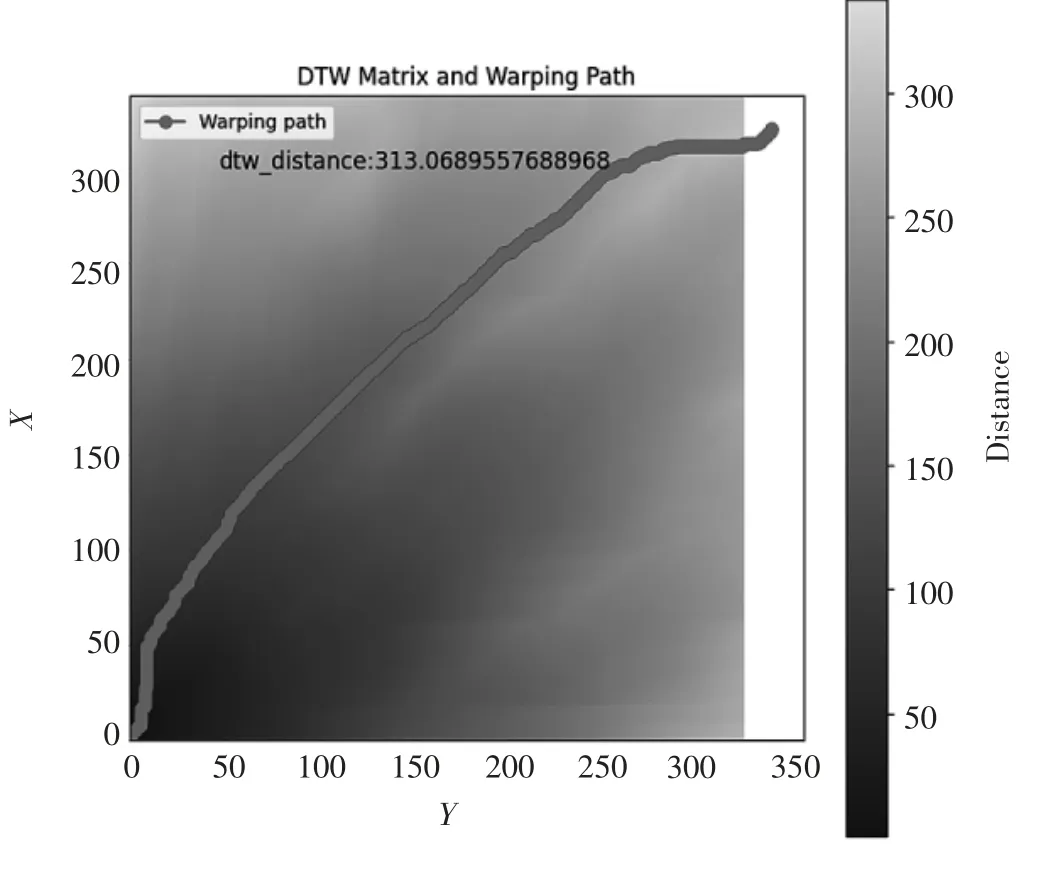
图3 参考批次与随机选择的批次差异性评价的结果

图4 进一步说明参考批次与其他99 个批次之间的差异性的一般结论，其中横坐标为批次数，纵坐标为每个批次的DTW 距离，灰色虚线为100 个批次与参考批次的平均DTW 距离，可以看出，99 个批次与参考批次之间平均DTW 距离为292.73，最小差异为251.63，最大差异为349.12，其中虚线的部分为被评价批次与参考批次距离的95%分位数，表明使用本文所提出的方法，任意批次与参考批次均可以计算出唯一的DTW距离，该距离能够表明被评价批次与参考批次的差异性，从而从量化地给出结论。

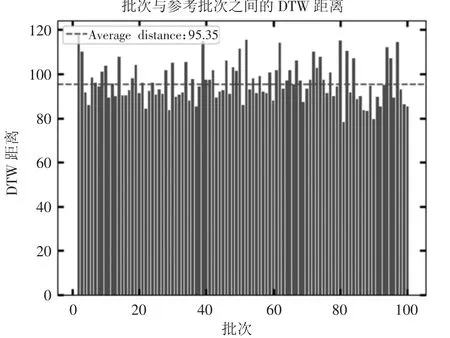
图4 参考批次与99 个被评价批次的距离汇总

为了更深入地理解一段时间内的生产总体情况，本文提出的方法可以与烟草行业广泛使用的统计过程控制（Statistical Process Control，SPC）方法相结合。SPC是一种通过统计分析来识别并控制生产过程中的质量变化的方法，以便实现稳定和预期的生产结果。在这种情况下，SPC 可以与我们的方法一起使用，以深入分析批次之间的差异性。

图5 是一个用于结合本文所提出方法与SPC 技术结合分析批次间差异性的统计控制图，其显示了批次间的差异随时间变化的情况，其中横坐标为批次数，纵坐标为每个批次的DTW 距离，统计控制图通常包括中心线（表示过程平均值或目标），以及上控制限（UCL）和下控制限（LCL），上规格限（USL）与下规格限（LSL），规格线和控制线可以根据历史生产状况自行确定，本图中使用2 个标准差确定规格线，3 个标准差确定控制线。

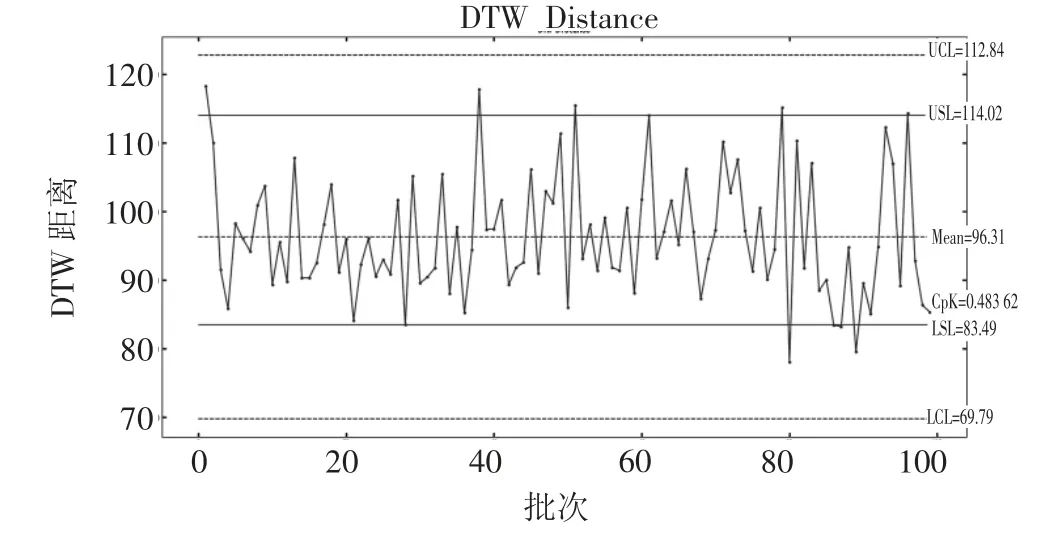
图5 使用SPC 控制图评价参考批次与99 个被评价批次之间的差异性

在图5 中，如果所有数据点都在UCL 和LCL 之间，那么可以认为过程在统计控制下，即过程稳定无特殊原因导致的变异；但是批次76 的数据点在UCL 或LCL 之外，这表示该批次出现了特殊原因的变异，需要进行调查和改进。进一步地，如果数据点出现系统性的、非随机的模式（例如连续上升或下降，或者出现周期性的波动），即使所有数据点都在控制限之内，也可能表示过程中存在潜在的问题，需要对这一段时间的生产进行重点关注。

4 结论

本文提出了使用动态时间规整（DTW）对多变量时间序列距离度量的方法，从而对制丝批次间差异评价，为烟草制丝质量控制提供了一种数据驱动的新思路。

在分析了烟草加工批次间差异的成因及其评价的意义，指出了统计模型、聚类、神经网络等传统异常检测方法在小样本场景下的局限性，在此基础上详细介绍了DTW 算法原理，并将其推广到处理多变量时间序列数据的场景，设计了利用DTW 距离来评价不同加工批次与优质批次差异的框架。

在实验部分，以卷烟生产中的松散回潮工序为例，应用所提方法对100 个批次进行了差异性评估并进行了可视化，验证了该方法的有效性。进一步结合统计过程控制相关技术，展示了所提出方法与传统SPC 技术的结合应用，以更全面地分析和控制批次间的质量差异；为烟草制丝质量控制提供了一种数据驱动的新思路，也可拓展至其他工业批次生产过程的质量评价与控制场景。

本研究的创新点在于，利用DTW 这种弹性时间序列匹配方法，可以有效地评价不同速率下时间序列数据的相似性，克服了传统方法的局限性，为烟草加工等小样本批次生产过程提供了新的质量分析手段。总体而言，研究工作具有良好的应用前景和推广价值。在实验部分，将所提出的方法应用到了卷烟生产中的松散回潮工序，并对100 个批次进行了差异性评估。结果表明，方法能有效地识别出批次之间的质量差异，并通过可视化的方式展现出这些差异。此外，本文还讨论了如何将本研究的方法与统计过程控制（SPC）相结合，以提供更深入的批次差异性分析。

本研究的方法提供了一种有效的工具，可以帮助卷烟生产企业更好地理解和控制制丝生产过程，从而提高产品质量的一致性和稳定性。同时，本方法也为其他需要处理多变量时间序列数据的工业生产场景提供了一个新的解决方案。尽管本方法在烟草制丝质量控制方面显示出了显著的效果，但其在其他领域的应用仍需要进一步研究和验证。