高维时变协高阶矩建模及其投资组合应用①
——基于半参数分布因子模型
2023-12-30黄光麟鲁万波
黄光麟, 鲁万波
(1. 西南财经大学统计学院, 成都 611130; 2. 西南财经大学管理科学与工程学院, 成都 611130)
0 引 言
国内外大量金融资产收益率的实证研究表明基于正态分布假设的传统建模方法不再适用[1-4].同时,这也导致了马克维茨的均值-方差分析和期望效用原则具有一致性的充分条件不再成立[5].马克维茨经典的均值-方差投资组合模型要求投资者效用函数为二次形式或者资产收益率分布服从正态分布,然而现有的大量研究表明这两个假设难以满足.一方面,Scott和Horvath认为将投资者的效用函数看作二次型并不恰当,他们指出在投资组合收益率分布是非对称或厚尾时,投资者无法利用二次形式效用函数刻画完全的分布形式,所以投资者必须考虑投资组合收益率的高阶矩,如偏度和峰度等[6].另一方面,Arrow的研究表明由于资产收益率分布的非正态性,二次效用函数并不能反映投资者绝对风险厌恶递减的特征,因此均值-方差投资组合面临着严重的福利损失[7].Dittmar,Mitton和Vorkink实证发现投资者愿意牺牲较小的收益和较大的波动性去换取一个正偏度和一个较小的峰度的投资组合[8].另外,国内大量文献证实了高阶矩在风险管理、经济预测和资产定价等方面发挥着重要的作用[9-11].
根据现有文献将高阶矩引入到投资组合中主要有两种方法:直接法和间接法.直接法是将资产投资组合收益率的高阶矩直接加入到均值-方差投资组合模型中作为目标函数,形成均值-方差-偏度或均值-方差-偏度-峰度投资组合模型[12].但由于直接法的经济含义模糊和多元非凸规划问题求解困难限制了直接法在高阶矩投资组合模型的发展和应用.间接法则通过泰勒展开,将投资者关注的函数展开为多项式形式,然后再给定阶数,通过优化这个多项式求解最优投资组合权重,这种方法将投资组合的均值-方差-偏度-峰度优化问题转化为一个包含均值、方差、偏度和峰度函数的优化问题.例如,以优化投资者期望效用(expected utility,EU)为目标[9,13];或以最优化投资组合的尾部风险为目标,例如在险价值(value-at-risk)和期望损失(expected shortfall),通过Cornish-Fisher展开为多项式进行优化[14,15].间接法的优点在于可以将多目标优化问题转化为投资组合各阶矩函数的单目标优化问题,能够直接反映投资者追求的目标和高阶矩对投资组合的边际影响,增加了求解的可行性,同时也保证了这种方法能够构造资产个数较多的投资组合,因此得到了广泛的应用.
综上所述,基于高阶矩的投资组合逐渐引起学者重视,但不可避免的会面临协高阶矩存在的“维数灾难”问题.“维数灾难”是由于待估参数过多导致的“估计不准”与“实现困难”.例如,包含15只股票的投资组合的协方差,协偏度,协峰度矩阵共有3 860个参数需要估计,这些待估参数还会随着资产规模增加呈指数型增长,而在时变协高阶矩的估计中,由于需要考虑高阶矩的时变结构,“维数灾难”的问题更加严重.目前,现有的时变高阶矩投资组合考虑的资产规模均小于15只[9,16,17].时变协高阶矩的估计困难大大限制了高阶矩投资组合在金融市场的应用.为了有效解决时变协高阶矩难估计,动态高阶矩投资组合难使用的问题,本研究提出了一种基于半参数分布时变因子(single factor time-varying semi-nonparametric,SF-TVSNP)模型的动态协高阶矩建模方法,一方面通过单因子模型有效缓解了协高阶矩估计的“维数灾难”问题,另一方面通过引入半参数分布减少模型可能存在的误设,增加模型稳健性.在因子模型设定恰当的情况下,各资产收益率可以用因子和异质性成分的线性组合解释,可以通过适当的分解将协高阶矩的时变结构拆分为因子的时变结构和各异质性成分的时变结构,然后分别进行估计.基于沪深300指数成分股的投资组合分析,本研究证实了SF-TVSNP模型存在的额外经济价值,以及它在投资组合中表现出的稳健性.
1 文献综述
对于本研究相关的文献综述将从两个视角展开:第一,作为因子模型在估计协高阶矩上的应用,有必要对基于因子模型估计协高阶矩的相关文献进行评述;第二,作为一种新的时变协高阶矩建模方法,需要对现有的时变协高阶矩估计文献进行评述.最后,本节将总结现有文献存在的问题以及本研究的创新点.
因子模型可以作为一个非常有效的途径来解决协高阶矩估计中存在的“维数灾难”问题.通过对资产收益率施加一个线性因子的结构,将协高阶矩的待估参数结构化,从而大大减少待估参数个数.例如,前文提到的包含15只股票的投资组合的前四阶协高阶矩有3 860个参数需要估计,利用一个三因子模型可以将其简化为96个参数.目前,根据资产定价方式不同,主要存在三种类型的因子模型:宏观因子模型、基本面因子模型和统计因子模型[18].但是,协高阶矩建模的高度复杂性与高度非线性使得现有的大部分因子建模方法集中在参数化的静态建模.Martellini和Ziemann将单因子模型拓展到了协高阶矩的估计,进一步给出了基于单因子模型的协高阶矩压缩估计[13].在利用多因子模型估计协高阶矩方面,目前有Boudt等基于可观测多因子模型和基于潜在因子模型讨论了静态协偏度和协峰度矩阵的估计,不仅在一定程度上缓解了“维数灾难”的问题,而且证明了样本外投资组合的优良性质[14, 15].但是,多因子模型在协高阶矩估计的使用存在一个关键性的问题—因子个数选择.Bailey等的研究表明,在现有的146个可观测因子中,市场因子(market factor)是唯一的强因子,而其他因子均为弱因子,这些弱因子只对部分资产具有解释能力,并且这种解释力随时间变化很大.因此,将这些弱因子不加选择的纳入因子模型中可能会适得其反[19].杨冬等给出了一种静态混频高阶矩框架下的因子个数选择方法,通过残差稀疏性检验选择正确的因子个数[20].从目前的研究来看,鲜有学者讨论具有时变协高阶矩结构下的因子个数选问题,这限制了多因子模型在时变协高阶矩上的应用.事实上,基于因子模型的时变协高阶矩建模也鲜有学者提及,其难点主要集中在条件协高阶矩的分解和时变结构的估计,这也使得基于因子模型的时变结构建模集中在协方差矩阵上[21-23].
对于多元金融资产收益的时变协高阶矩建模,多数文献将其转化为多个具有相关结构的单变量高阶矩时变模型进行建模.主流的单变量时变高阶矩模型有两种:第一种是Hansen提出的自回归条件密度(ARCD)模型,该模型中驱动高阶矩参数具有GARCH模型的动态结构,利用极大似然估计方法,估计出形状参数时变方程中的参数从而得到时变的形状参数,因此资产收益率的高阶矩也是动态的[24];第二种是León等提出的GARCHSK模型,它对金融资产收益率的波动率,偏度和峰度的时变结构直接建模,同样赋予它们一种GARCH结构,但是GARCHSK模型假设金融收益率的分布函数为正态分布Gram-Charlier(GC)级数展开,因此它是一种基于时变高阶矩的近似模型[25].上述两种单变量模型各有优劣,GARCHSK模型无需指定分布从而更加稳健,ARCD模型则有渐进理论支撑其有效性.两种模型都被广泛应用到时变协高阶矩建模中.例如,Jondeau和Rockinger将协高阶矩的动态结构分解为不同资产收益率之间相关性的动态结构和单个资产收益率高阶矩的动态结构.他们的研究将动态条件相关(DCC)模型与ARCD模型相结合,是DCC模型在协高阶矩上的扩展[16].Ghalanos等通过独立成分分析(ICA)将金融资产收益率转化为潜在独立因素,然后估计各独立因素边际密度的高阶矩时变参数,进而估计这些独立因素的高阶矩的动态结构[17].他们的研究是广义正交GARCH(GO-GARCH)模型在协高阶矩上的扩展,利用ICA与数个单变量ARCD模型相结合对多元金融资产收益率的协高阶矩的动态结构建模,称之为GO-ARCD模型.蒋翠侠等则以ICA的思路拓展了GARCHSK模型,提出了独立成分GARCHSK(ICASK)模型,并将其应用到动态投资组合分析中[9].目前对于时变协高阶矩建模的相关文献仍然匮乏,并且存在以下几个问题:首先,绝大多数文献都采用ICA或DCC的降维方式将时变协高阶矩建模转化为数个独立潜在序列的时变高阶矩建模,当投资组合维数N较高时,上述文献仍然不能解决“维数灾难”的问题,ICA和DCC降维方式的待估参数个数都是以O(N2)增加,当资产维数较高时模型仍然难以估计;其次,由于部分金融资产收益率极端倾斜厚尾(例如偏度绝对值大于1,峰度大于20)的特点,利用现有的已知分布(例如偏斜学生t分布或偏斜广义误差分布)已无法对其高阶矩进行拟合,因此可能存在严重的模型误设,进而导致估计量不稳健.
综上所述,可以总结出本文的创新点如下:第一,通过因子模型的降维手段更好地捕捉了多元资产收率的潜在结构,解决了现有时变协高阶矩建模仍无法解决的“维数灾难”问题,使动态高阶矩投资组合能够应用于高维场景.第二,为减少时变高阶矩建模可能产生的分布误设,引入一种半参数分布对时变高阶矩建模,增加了模型的稳健性和适用性;同时,通过对因子和各资产的异质性成分进行时变高阶矩建模,而非资产收益率本身,前者拥有更温和的偏度和峰度,保证了模型的可估计性.第三,将静态因子协高阶矩估计拓展到时变协高阶矩的估计中,丰富了因子模型相关理论研究.
2 半参数分布时变因子模型及其估计
2.1 模型形式
本研究考虑的半参数分布时变因子(SF-TVSNP)模型如下
(1)
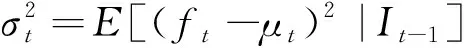

(2)
其中rt=[r1t,r2t,…,rNt]T,u=[u1,u2,…,uN]T,B=[β1,β2,…,βN]T,εt=[ε1t,ε2t,…,εNt]T均为N×1的向量;ht与t分别为条件标准差与标准化异质性成分的向量表达;“∘”表示Hadamard内积.
2.2 半参数分布及其条件高阶矩
由于zt及it都服从标准化后的TVSNP分布,为方便起见,先从一般形式的TVSNP分布进行介绍,记TVSNP分布的概率密度函数为
q(xt,θt)=λtφ(xt)ψ2(xt,θt)
(3)
其中xt∈,θt=[θ1t,θ2t]T为参数向量,φ(·)为标准正态分布密度函数,ψ(·)定义如下
(4)
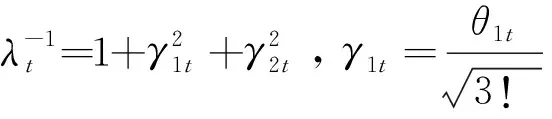
Eq[xt|It-1]=4λtγ1tγ2t
(5)
因此,标准化的TVSNP随机变量可以定义为zt=a(θt)+b(θt)xt,其中
a(θt)=-b(θt)Eq[xt|It-1]
(6)
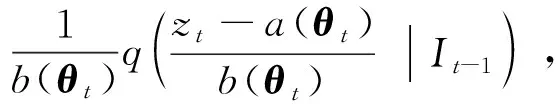
sz,t=Eq[(at+btxt)3|It-1]
=Eq[(at+btxt)3|It-1]-3
(7)
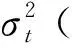
2.3 时变结构方程的设定
本研究需要对因子的条件均值μt(φ),条件方差σt(φ),以及形状参数θt(ϑ)的时变结构进行设定,其中φ为驱动因子条件均值μt与条件方差σt的时变结构参数,ϑ为驱动因子形状参数θt的时变结构参数.类似的,对于每一个异质性成分εit则需要对其条件方差hit(υi)以及形状参数ηit(ζi)的时变结构进行设定,其中υi与ζi分别为驱动hit和ηit的时变结构参数.对于因子的时变结构设定如下
μt=ρ0+ρ1μt-1+ρ2ft-1
(8)
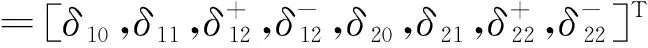
ηd,it=τd,i0+τd,i1ηd,it-1+

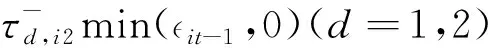
(9)
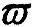
2.4 因子载荷的估计
由于异质性成分之间相互独立,因子载荷矩阵B的估计可以由N个OLS回归一致估计,具体来说,对于资产i有
(10)
2.5 因子时变结构的估计
对于因子的时变参数可以通过极大似然估计完成.但是,由于高阶矩时变结构的高度非线性化,直接同时估计均值、方差、高阶矩方程较为困难.许多学者建议在参数估计过程中可以按照“简单到复杂”的原则来进行多阶段的估计,即先估计均值-方差方程中的参数,然后再将其得到的结果作为高阶矩方程的初始值[26,27,29-31].本研究参照León和íguez[26, 27],王鹏[29]采用的两阶段估计对因子的时变结构进行估计.具体来说,由式(1)和式(3)可知因子的条件概率密度函数为
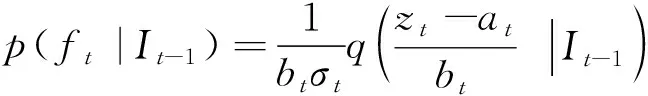
(11)
其中at=a(θt(ϑ))和bt=b(θt(ϑ))的定义在2.2节给出,θt(ϑ)=[θ1t(ϑ),θ2t(ϑ)]T为It-1可测的参数向量,ϑ为θt时变结构方程中的待估参数.于是TVSNP模型的样本对数似然函数为
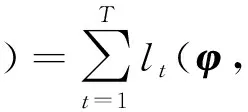

lnσt(φ)-lnb(θt)
(12)
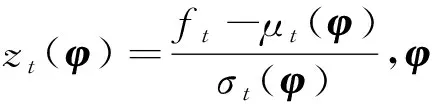

lnσt(φ)
(13)
2.6 异质性成分时变结构的估计
由于异质性成分的时变结构设定与因子类似,可以参考2.5节的估计方法对N个异质性成分的时变参数进行估计,需要注意的是,异质性成分不包含时变的均值结构且基于估计的异质性成分,其似然函数如下
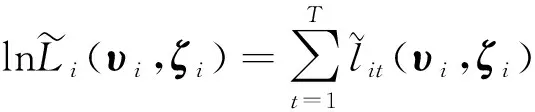
(14)
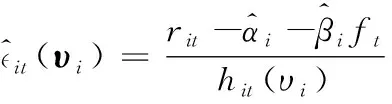
1)随样本长度T→∞,
2)随样本长度T→∞,
lnLi(υi,ζi)|→0 a.s.
3 时变协高阶矩的估计与识别
基于第2节对于SF-TVSNP模型参数的估计,本节给出资产收益率的时变协高阶矩的估计方法.
3.1 时变协高阶矩表示及其分解
参考Jondeau和Rockinger[28]引入的高阶矩张量记法,将资产收益率的条件协方差矩阵,条件协偏度矩阵,条件协峰度矩阵中的元素定义如下
σij,t=E[(rit-mit)(rjt-mjt)|It-1]
sijk,t=E[(rit-mit)(rjt-mjt)(rkt-mkt)|It-1]
kijkl,t=E[(rit-mit)(rjt-mjt)(rkt-mkt)
(rlt-mlt)|It-1]
(15)
因此,它们的矩阵表达式为
Σt=E[(rt-mt)(rt-mt)T|It-1]
={σij,t}N×N
St=E[(rt-mt)(rt-mt)T⊗(rt-mt)T|It-1]
={sijk,t}N×N2
Kt=E[(rt-mt)(rt-mt)T⊗(rt-mt)T⊗
(rt-mt)T|It-1]={kijkl,t}N×N3
(16)
进一步,定义协超额峰度矩阵EKt,其中的元素为
ekijkl,t=kijkl,t-σij,tσkl,t-σik,tσjl,t-σil,tσjk,t
(17)
其矩阵表达为EKt={ekijkl,t}N×N3.接下来考虑对条件协方差矩阵,条件协偏度矩阵,条件协峰度矩阵进行分解,以协方差矩阵为例,由式(15)有
σij,t=E[(rit-mit)(rjt-mjt)|It-1]
=E[(βiσtzt+εit)(βjσtzt+εjt)|It-1]
E[βiσtztεjt|It-1]+E[βjσtztεit|It-1]+
E[εitεjt|It-1]
(18)
同理对条件协偏度矩阵分解有
sijk,t=E[(rit-mit)(rjt-mjt)(rkt-mkt)|It-1]
=E[(βiσtzt+εit)(βjσtzt+εjt)×
(βkσtzt+εkt)|It-1]
(19)

ekijkl,t=kijkl,t-σij,tσkl,t-σik,tσjl,t-σil,tσjk,t
=E[(rit-mit)(rjt-mjt)(rkt-mkt)(rlt-mlt)|It-1]-
σij,tσkl,t-σik,tσjl,t-σil,tσjk,t

E[εitεjt|It-1]E[εktεlt|It-1]-E[εitεkt|It-1]
E[εjtεlt|It-1]-E[εitεlt|It-1]E[εjtεkt|It-1]
(20)
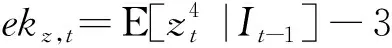
(21)

{Kt}ijkl={EKt}ijkl+σij,tσkl,t+σik,tσjl,t+
σil,tσjk,t
(22)
3.2 条件协高阶矩的估计
通过2.4 节~ 2.6节分别对于因子载荷、因子时变结构以及异质性成分时变结构的估计,结合式(21)对于时变协高阶矩的分解,可以得到金融资产收益率的条件协高阶矩如下
(23)
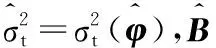
(24)
3.3 时变高阶矩的识别检验
建立时变高阶矩模型的首要前提是对应序列分布的偏度和峰度具有时变特征,即序列存在类似于条件异方差性的条件异偏度和条件异峰度特征.现有文献中涉及检验资产收益率序列是否存在异偏度和异峰度特征的研究主要集中在两种框架:第一类方法是先估计某种时变高阶矩模型(如GARCHSK模型和ARCD模型),再通过检验与时变偏度和时变峰度对应的时变系数的显著性来判断资产收益率序列是否存在异偏度和异峰度特征,这其中常用的检验有瓦尔德(Wald)检验和似然比(LR)检验[26,32];第二类方法是对资产收益率序列拟合GARCH模型后得到的残差或者标准化残差来进行回归检验,例如Jondeau和Rockinger[28]类比ARCH效应检验对标准化残差的三次方和四次方序列对其滞后项构造LM统计量进行检验,贾婧等[33]则通过概率积分变换改进了Jondeau和Rockinger的LM统计量,取得了更高的功效.
SF-TVSNP模型需要分别对因子与异质性成分进行时变高阶矩识别检验,参考Vuong[34]和León和íguez[26]的方法,本研究通过构建似然比检验对时变高阶矩进行识别.具体来说,似然比检验通过比较TVSNP模型与嵌套的CSNP模型的对数似然函数值进行检验,对于因子的时变高阶矩检验有如下结论
(25)
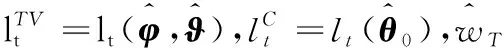
(26)
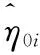
3.4 维数灾难
由于时变高阶矩建模面临着严重的“维数灾难”问题,如何将时变高阶矩投资组合应用到高维场景成为一大难题.时变高阶矩建模的“维数灾难”问题主要体现在“估计不准”与“实现困难”上.“估计不准”是指待估参数过多导致估计量自由度小、方差大.“实现困难”是指大量参数估计需要占用大量内存与时间,尤其高阶矩参数估计具有高度非线性的特点,进一步增加了估计难度.
4 模拟研究
本节通过构建蒙特卡洛模拟对SF-TVSNP模型的有限样本性质进行验证,主要集中在SF-TVSNP模型的稳健性.SF-TVSNP模型使用时变半参数分布(TVSNP)对因子与异质性成分的高阶矩时变结构建模,放松了对分布的假定,与之对应的是需要给定分布的自回归条件密度(ARCD)模型.Ghalanos等采用偏学生t(SST)分布与偏广义误差(SGE)分布进行ARCD建模,进而估计金融资产收益率的条件高阶矩.但是,由于真实数据的条件分布未知,错误的给定条件分布可能会导致严重的模型误设问题,进而导致估计结果不稳健.本节将会比较TVSNP模型与给定分布的ARCD模型对于条件高阶矩的估计.
为使模拟更具真实性,本节的模拟数据通过真实数据参数校准的方法给出.由于因子与异质性成分建模方法相同,限于篇幅本节只对因子的条件高阶矩进行模拟估计.用于参数校准的数据为2005年7月1日至2019年6月30日的沪深300指数.本节的模拟步骤如下.
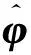
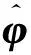
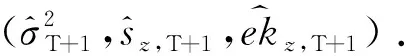
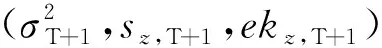
表1汇报了T=1 000时,重复500次模拟后各方法RMSE的均值与标准差.当真实分布分别为SGE与SST时,基于SNP分布的条件矩估计表现基本相同,受真实分布设定影响很小.对于基于SST分布的ARCD模型,当真实分布为SGE时,在估计条件偏度与条件峰度存在较大偏误,同时条件峰度RMSE的标准差较大,估计量由于模型误设的原因非常不稳定.另外,在所有方法中,基于SNP分布的RMSE拥有最小的标准差,进一步体现了其稳健性.
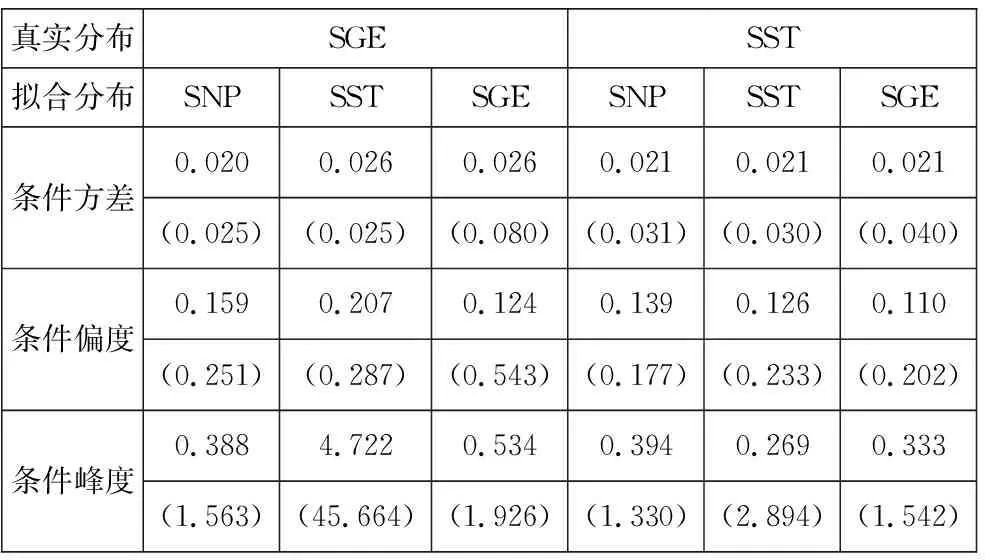
表1 不同分布设定下条件矩估计量的RMSETable 1 RMSE of conditional moments under different distribution specifications
5 实证分析
5.1 动态高阶矩投资组合
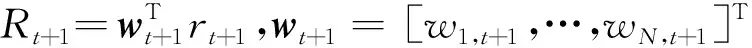
(27)
其中μt+1,Σt+1,St+1,Kt+1为资产收益率向量rt+1的前四阶条件协高阶矩;α,B为SF-TVSNP模型中的截距与因子载荷.参考Martellini和Ziemann[13],Jondeau和Rockinger[16]对于常相对风险厌恶效用函数(constant relative risk aversion,CRRA)的前四阶展开,可以得到期望效用表达式为
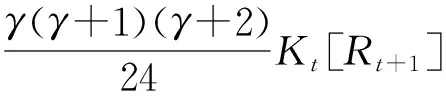
(28)
其中γ为常相对风险厌恶的测度参数,通过最大化式(28),可以得到t+1时刻基于期望效用最大化的最优投资组合.另外,通过对t+1时刻的条件VaR进行四阶Cornish-Fisher展开,本研究可以得到修正VaR表达式为
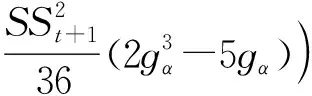
(29)
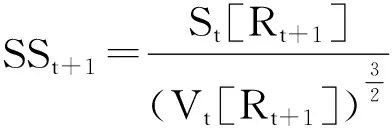
5.2 数据与实证设计
为了保证本文中的研究具有代表性,充分反映中国股票市场中可能存在的高阶矩特征,本文对沪深300指数中成分股进行分析,参照中证指数有限公司对于沪深300指数的编制表,以2018年5月31日的成分股列表作为依据,将2005年7月1日至2019年6月30日的上市股票日度收益率(样本长度为3 403日)作为研究对象.由于时间跨度大,部分成分股上市较晚或已退市以及一部分成分股有长时间停盘,本研究保留缺失值不超过3年,共计206只成分股作为研究对象.对于少量股票在样本初期并未上市的股票,将会在其上市后被纳入投资组合中.另外,本研究选择沪深300指数作为市场因子的代理变量.表2对因子与成分股进行了描述性统计,由于成分股较多,本研究展示了成分股对应统计量的分布特征.从表2可以发现,指数相较于成分股拥有更温和的偏度与峰度.同时所有序列都平稳且具有非正态性,这是金融资产收益率的典型特征.
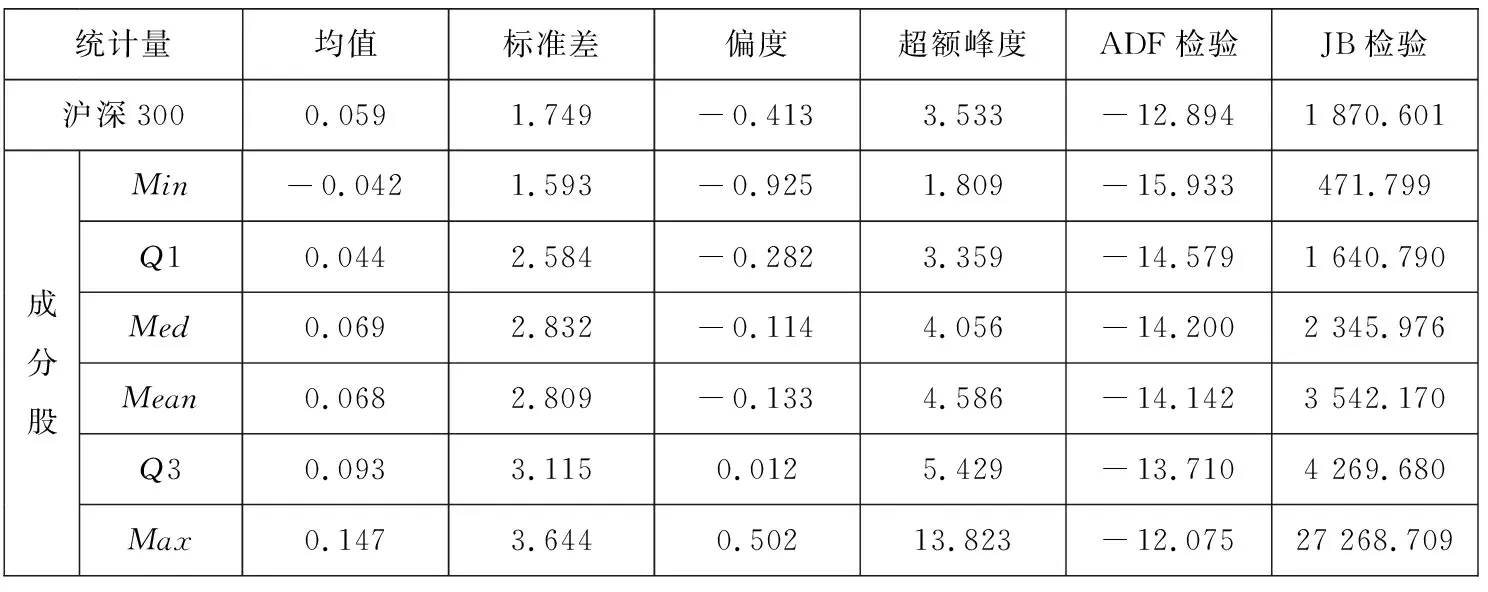
表2 收益率序列描述性统计Table 2 Descriptive statistics of asset returns
为减少样本选择偏误,使结果更具一般性,本文的实证设计参考了Martellini和Ziemann[13]的投资组合研究.具体来说,本研究将206只沪深300成分股看作一篮子股票,将2010年1月1日—2019年6月30日作为样本外区间,每一年从篮子中随机抽取资产个数N的投资组合,因此,对于每一种资产规模N,样本外区间中每一年的投资组合都不同,基于此,本研究完成整个样本外区间的回测,进而通过分析10年样本外表现得到最终结果.为保证有充足的数据对模型进行估计,使用样本外区间前5年的日度数据来估计投资组合的时变协高阶矩,并通过滚动窗口估计给出下一日的最优投资组合权重,并将该投资组合持有一周.因此,本研究得到了10年共2 305日(464周)样本外投资组合.最后,通过5.1节介绍的高阶矩投资组合函数(EU)对样本外投资组合进行优化,对优化后的样本外收益率和投资权重进行分析.
为更好刻画SF-TVSNP模型对于“维数灾难”问题的解决,本文选择N=10与N=100分别代表低维与高维投资组合,目前动态高阶矩投资组合的资产规模集中在N<15上[9,16,17],鲜有文献对于高维动态高阶矩投资组合进行实证研究.
5.3 因子与异质性成分的时变高阶矩估计
因子与异质性成分的时变高阶矩特征是SF-TVSNP模型的核心,在进行动态投资组合分析前,有必要对这两部分的估计结果进行分析.需要注意的是,在每一种资产规模下,本文随机抽取部分股票构建投资组合,而因子在整个实证分析中是唯一的.为了在有限篇幅下展示市场的时变高阶矩特征,本研究主要对因子的TVSNP模型估计结果进行分析,异质性成分的时变高阶矩特征则会通过时变性检验的方式呈现.
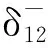

表3 沪深300指数TVSNP模型估计结果Table 3 Estimated TVSNP coefficients of CSI300
进一步,基于TVSNP和CSNP的估计结果,图1给出了沪深300指数的条件高阶矩在样本内的变化趋势.可以很明显的观察到TVSNP模型捕捉到了指数在样本内的时变高阶矩特征,当股灾发生时,条件偏度和条件峰度出现了类似于波动率的聚集性,其中条件偏度为负向聚集.CSNP模型则无法对高阶矩时变特征进行估计,比较两者结果可以直观感受到对高阶矩进行时变结构建模的优越性.
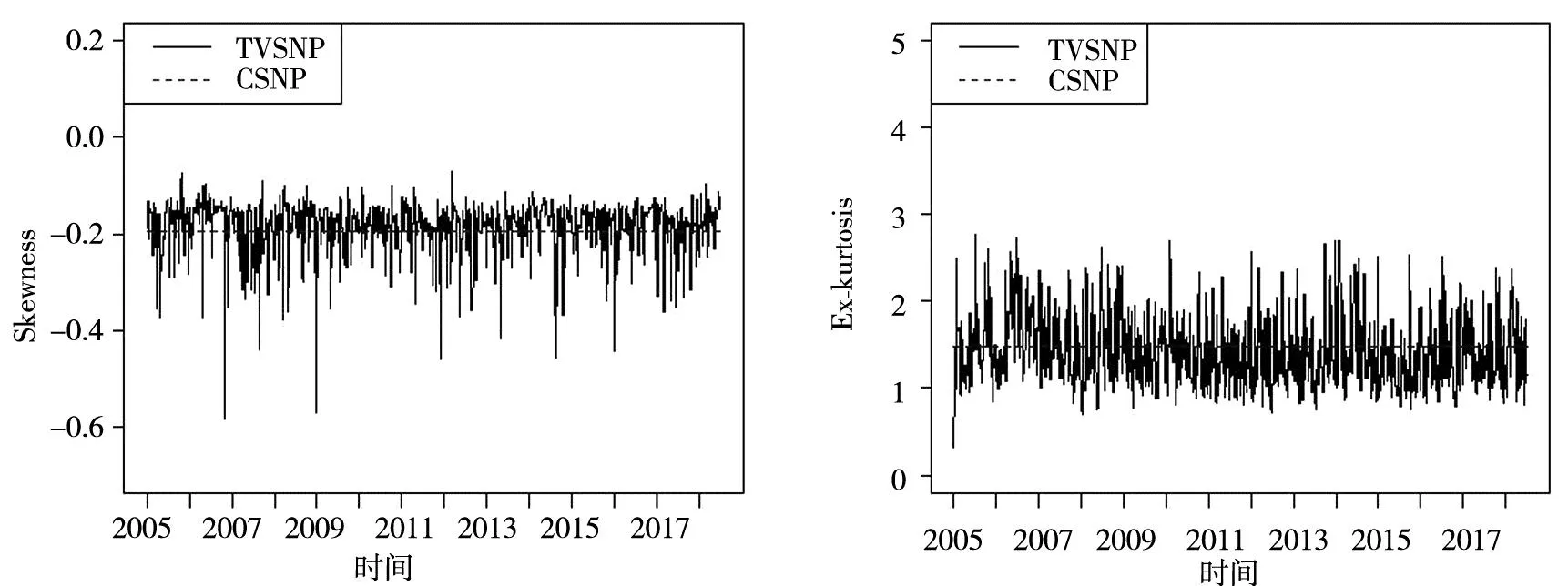
图1 沪深300指数时变高阶矩特征Fig.1 Time varying higher-order moments of CSI300
对于异质性成分的时变高阶矩分析主要通过假设检验进行,为使研究结果更具一般性,本研究对样本区间内206只成分股的异质性成分进行时变高阶矩检验,显著性水平α分别取10%,5%,1%.由于该检验为多重检验(multiple test)问题,本文采用Sidák方法对显著性水平进行校正,即αcorr=1-(1-α)n,其中n=206为检验个数.本文分别对各异质性成分的时变异方差性,常高阶矩性与时变高阶矩性进行检验:时变异方差检验通ARCH检验完成,常高阶矩检验通过对η0i的t检验完成,时变高阶矩检验通过式(26)的似然比检验完成.
表4汇报了所有异质性成分中上述三种检验显著的频率,可以看到异质性成分的时变异方差性与常高阶矩性普遍存在,但高阶矩时变结构并不是普遍存在的,在1%显著性水平下,只有1.46%股票的异质性成分拒绝了原假设.这意味着SF-TVSNP模型可以对异质性成分的时变结构进行简化,只需要对时变异方差与常高阶矩进行建模,本文将在下一节进行验证.
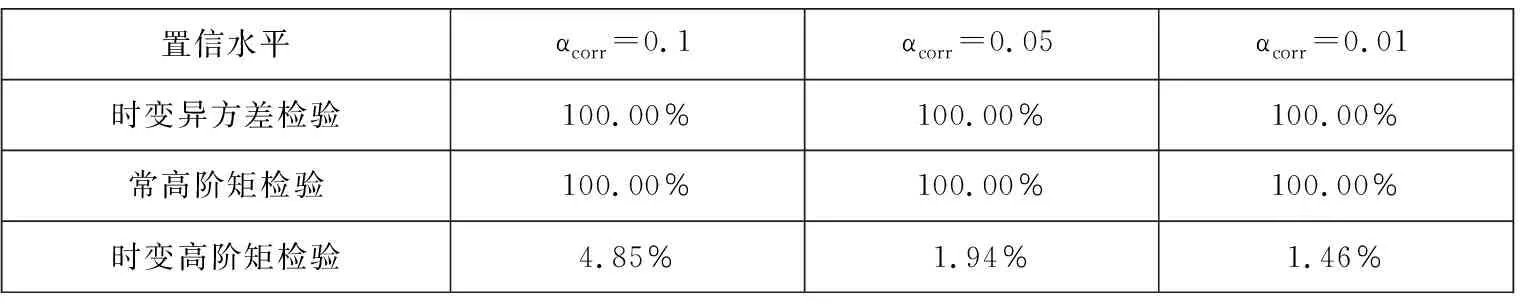
表4 资产异质性成分假设检验频率统计Table 4 Frequency summary of the LR statistics of the idiosyncratic errors
5.4 动态投资组合分析
本节的投资组合分析遵循5.2节的实证设计.通过5.3节的时变高阶矩特征分析,基于异质性成分时变高阶矩特征不是普遍存在的事实,本文考虑了异质性成分为常数半参数分布的SF-ECSNP(sF-error constant SNP)模型作为SF-TVSNP的嵌套模型.为了充分体现SF-TVSNP模型在动态投资组合的经济价值,本文从横纵两个方向选取现有模型进行比较.从纵向看,SF-TVSNP模型可以看作Martellini和Ziemann[13]提出的静态单因子(SF)协高阶矩估计在动态结构上的改进,因此SF估计可以作为纵向比较的门槛(Benchmark)模型;从横向看,SF-TVSNP 模型需要与其他时变协高阶矩模型比较优劣,本研究选取了指数加权移动平均(EWMA)模型(2)EWMA模型中的移动平均参数设定为0.95.,以及ICASK模型[9]作为横向比较的门槛模型.同时,本研究同样考虑均值-方差投资组合(MV)作为门槛模型,协方差矩阵由单因子模型估计得到.从投资组合的角度,本研究选取了等权重(EW)投资组合作为投资组合门槛模型.
本研究通过以下指标来衡量样本外投资组合的表现: 1)年化收益率; 2)年化标准差; 3)修正风险价值(Modified VaR); 4)标准化偏度与超额峰度; 5)年化夏普比率; 6)换手率(Turnover); 7)最大回撤(Max Drawdown).其中修正风险价值定义如式(29)所示,换手率定义为
(30)
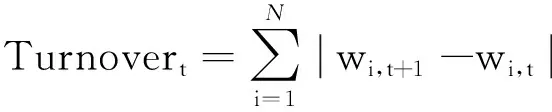
(31)
其中c为交易费率,设定为0.5%.在计算夏普比率时,本文选择央行公布的一年定存基准利率作为市场无风险利率.本节中动态投资组合目标函数为CARA效用函数(γ=10),同时投资组合不考虑卖空(∀wi≥0).
表5给出了不同方法与不同资产规模(N=10与N=100)下样本外投资组合的表现.需要注意,当N=100时,ICASK与EWMA模型由于“维数灾难”的原因无法实现,因此本研究将其略去.从表5中总结出以下几点结论:1)以考虑交易费用后的夏普比率与最大回撤率作为评价标准,在所有资产规模下,SF-TVSNP(SF-ECSNP)投资组合有着最优表现,同时SF-TVSNP与SF-TVSNP表现基本一致,这与表3的结论相符,对异质性成分的动态高阶矩建模产生的额外收益甚微; 2) 相较于其他动态投资组合, SF-TVSNP投资组合的表现更加稳健,体现在拥有更小的年化标准差、风险价值与最大回撤.当N=10时,尽管ICASK拥有较高的年化收益,但伴随的时较高的投资风险(39.278%的年化标准差,4.011%的风险价值与74.271%的最大回撤),而SF-TVSNP的风险指标均大幅优于ICASK,体现了该方法的稳健性.当N=100时,SF-TVSNP投资组合的各项风险指标均为最优,充分体现了SF-TVSNP模型所具有的额外经济价值; 3)随着N从10增加到100,各投资组合风险指标均得到改善,体现了高维投资组合能够更好的分散风险的特点,其中SF-TVSNP投资组合的改进幅度最大;4)相较于ICASK投资组合,SF-TVSNP有着相对较小的换手率,同时静态投资组合比动态投资组合有着更小的换手率,这与Martellini和Ziemann[13]的结论一致.随着N增大,SF-TVSNP投资组合与SF和MV投资组合换手率之间的差距减小.
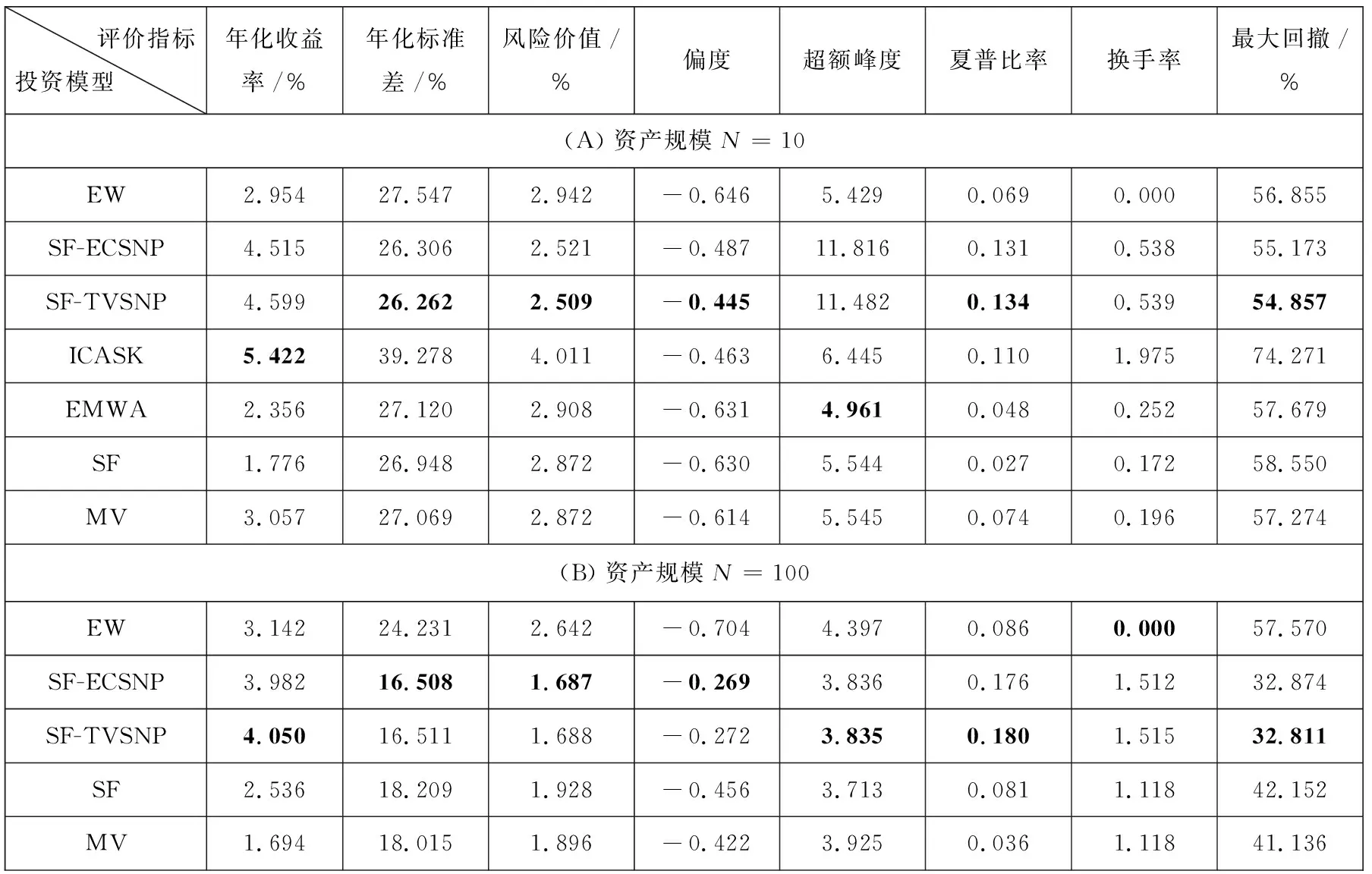
表5 样本外投资组合表现Table 5 Out of sample portfolio performance
综合以上结论可以得到SF-TVSNP(SF-ECSNP)模型相较于现有的动态(静态)协高阶矩估计方法有着更高的经济价值.纵向来看,引入了因子与异质性成分的高阶矩时变结构的SF-TVSNP模型对静态因子模型进行了改进;横向来看,因子模型相较于独立成分分析更加适合解决协高阶矩的“维数灾难”问题,这体现在 SF-ECSNP模型相较于ICASK模型有更优且更稳定的表现,同时SF-ECSNP模型能够应用于高维投资组合,有利于更好的分散风险.
5.5 稳健性分析
本节将评估5.4节的实证结果对实证设计和参数设定的各种变化的敏感性.具体来说,本研究考虑了以下四种不同的设定并探究其对动态投资组合结果的影响.
1)考虑到因子和异质性成分的条件异方差结构可能存在的非对称效应和杠杆效应,本文考虑了GJR-GARCH(1,1)和TGARCH(1,1)拟合条件异方差结构.GJR-GARCH的设定如下
(32)
GJR-GARCH能够捕捉到一个 GARCH 模型无法描述的实证现象,即t-1时刻的负面冲击比正面冲击对t时刻的方差有更强烈的影响,即杠杆效应.TGARCH则通过一个分段结构对条件方差中的非对称效应进行拟合,其设定如下
(33)
2)投资组合优化函数中参数设定直接反映了投资者的偏好,例如CRRA期望效用函数中的γ参数反映了投资者的风险厌恶程度,本研究进而考虑了γ=1(较低风险厌恶程度)和γ=15(较高风险厌恶程度)时投资组合的表现.
3)考虑以式(29)的VaR函数作为投资组合优化函数.VaR函数中α代表优化的风险价值的水平,越小的α代表着越高的对于极端风险的承受能力,本文在稳健性分析中取α=0.01与α=0.05.
4)本文考虑了样本长度对于估计结果的影响.为了不改变样本外区间(2010年1月1日—2019年6月30日),本文选择了如下两种不同的滚动样本: 第一,仍然以2005年7月1日—2009年12月31日作为起始估计,但采用递归样本对样本外区间进行滚动估计;第二,以2006年1月1日—2009年12月31日(共4年日度数据)作为起始估计,仍然采用滚动窗口方式对样本外区间进行滚动估计.两种方法分别对应着较多和较少的样本长度.
为使稳健性分析更具代表性,减少样本选择偏误,本研究仅考虑高维投资组合(N=100),同时由于SF-ECSNP与SF-TVSNP模型表现基本一致,限于篇幅,本文仅汇报上述设定对SF-ECSNP模型的影响,评价标准仍然采用5.4节介绍的评价指标.表6给出了上述四种稳健性检验的样本外表现.对于检验1),采用GJR-GARCH或TGARCH设定后,SF-ECSNP的表现有所提升,这与理论相符,由于GJR-GARCH与TGARCH捕捉到了条件异方差结构的杠杆效应,进而提升了投资组合整体表现;对于检验2)与检验3),表6的结论与表5基本保持一致,即SF-ECSNP模型对于目标函数与风险厌恶程度具有稳健性;对于检验4),4年期滚动窗口会使投资组合表现小幅降低,这是由于时变结构的估计需要较大样本量支持,尤其是时变高阶矩结构方程的估计.另一方面,当采用递归样本进行样本外投资组合时,年化收益率与夏普比率有所提升,但各项风险指标有所下降,可能原因是数据时间跨度太长,例如始终包含2008年次贷危机的极端数据对模型进行估计,这不利于估计过程中新的结构进入.综合稳健性分析的结果,SF-ECSNP模型的各项风险指标表现具有稳健性,这与蒙特卡洛模拟的结论一致,通过引入半参数分布保证了条件高阶矩估计量的稳健性,进而保证了动态投资组合稳定的超额收益.另外,根据稳健性分析的结果,可以通过引入GJR-GARCH(或TGARCH)结构改进动态投资组合表现.
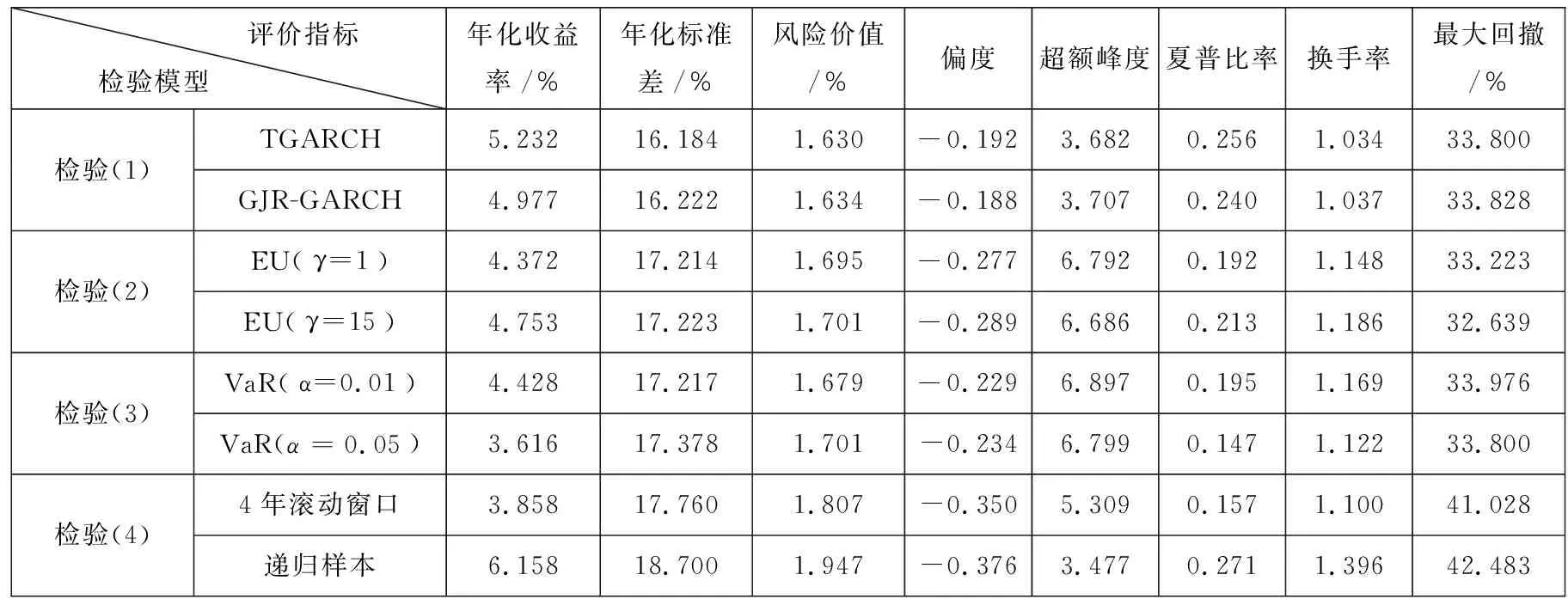
表6 SF-ECSNP投资组合的稳健性分析Table 6 The robust checks of the SF-ECSNP portfolio
6 结束语
基于协高阶矩的投资组合研究不可避免的需要解决协高阶矩估计存在的“维数灾难”问题.在时变协高阶矩建模中,绝大多数学者都采用独立成分分析或动态条件相关的方式进行降维,将多维时变协高阶矩建模转化为多个独立潜在序列的时变高阶矩建模,由于其假设的严苛和复杂的计算,这类模型在现实数据的表现并不好,只能用于低维投资组合且可能存在严重的模型误设问题.因此本研究提出了一种基于半参数分布因子(SF-TVSNP)模型的时变协高阶矩建模方法,通过因子结构对时变协高阶矩进行分解降维,同时引入半参数分布提高模型的稳健性.本研究在Martellini和Ziemann的静态单因子协高阶矩估计中,赋予因子与异质性成分时变半参数分布,对时变半参数分布的形状参数进行建模,通过OLS回归和两阶段极大似然估计分别估计了因子载荷,因子时变结构和异质性成分时变结构.进一步通过协高阶矩在因子模型下的分解,最终给出了时变协高阶矩的估计.蒙特卡洛模拟证实了时变半参数分布建模的稳健性.基于沪深300指数成分股的动态投资组合分析和稳健性检验证实了SF-TVSNP模型存在稳定的、额外的经济价值.
主要研究结果: 1)通过建立SF-TVSNP模型估计金融资产收益率的时变协高阶矩,给出了模型设定,估计和时变高阶矩时变检验方法,丰富了时变协高阶矩估计相关文献; 2)实证分析表明,沪深300指数存在显著时变高阶矩特征,并且呈现出类似于波动率的聚集性,当金融危机发生时,条件偏度会负向聚集,而条件峰度会正向聚集.同时,其成分股异质性成分的时变高阶矩特征并不普遍存在,基于此,本研究构建更加容易估计的SF-ECSNP模型; 3)相比于现有动态(静态)协高阶矩估计方法,基于SF-TVSNP模型的投资组合有更优的样本外表现,各项风险指标均优于现有方法.同时,SF-TVSNP模型能够应用于高维投资组合(N=100),实现了高维动态高阶矩投资组合; 4)基于SF-TVSNP模型的投资组合通过了稳健性检验,其表现基本不会受到用户设定的影响.本研究提供了一种更合理、表现更好、更稳定的高维时变协高阶矩建模方法.基于研究结论,可以为市场投资参与者和市场监督管理者提供风险管理技术和科学决策依据.
