基于融合数据自表示的离群点检测算法
2023-12-30高亚星赵旭俊曹栩阳
高亚星,赵旭俊,曹栩阳
(太原科技大学 计算机科学与技术学院,山西 太原 030024)
0 引 言
离群数据是指与其他数据分布有显著不同的数据对象[1]。离群点检测是通过分析离群数据的特征,从海量数据中挖掘异常信息和提取兴趣模式的一种方法,已广泛地应用在欺诈检测[2]、入侵检测[3]、疾病检测[4]、时间序列离群值检测[5]等领域。
基于数据自表示的离群点检测[6]是一种有效的方法,该方法通过构建数据点间的稀疏表示,放大了数据间的差异性,在低维离群点检测上有较好的性能。但该方法仍存在一定的局限性,导致其在高维数据上的离群点检测效果不佳。随着数据量和数据维度的急速攀升,解决该问题是十分必要的。
基于数据自表示的离群点检测方法通过研究低维数据间的关联性与稀疏性,并构建表示关系,在低维全局离群点检测上获得了较好的效果。但该方法在处理高维数据时存在以下两点问题:第一,高维数据相较于低维数据会更加离散,使得该方法更难得出较为准确的数据表示,从而影响高维离群点检测的效果;第二,该方法并未考虑特征间的关联性对数据相互表示过程的影响,在处理低维数据时,这种局限性对检测结果影响并不大,然而高维数据中特征间的复杂关系不容忽视,这些特征关系对离群点的检测有较大影响,该方法的局限性被进一步放大。
为了解决以上问题,该文提出了一种基于融合数据自表示的离群点测检算法。首先,使用文献[7]提出的特征分组方法对数据集按照相关特征进行分组,达到数据约简的目的。其次,提出一种基于特征关系的数据自表示方法,在每个特征分组内,运用信息理论度量特征间的关联性,构建了包含特征和数据双重信息的数据自表示矩阵。然后,提出一种基于融合组间数据自表示的计算方法,将不同特征分组和组中心特征集对应的数据自表示矩阵相融合,采用矩阵点乘和均值计算得出全局自表示矩阵,其包含了丰富的全局数据特征和数据信息。最后,提出了基于融合数据自表示的离群点测检算法,该算法在全局数据自表示矩阵上构建了有向加权图,并通过在该图上随机游走来检测离群点。在多个真实数据集和人工合成数据集上的实验结果表明,该算法具有良好的泛化性和稳定性。
1 相关工作
目前,传统离群点检测算法主要分为四大类,分别是基于密度的方法[8]、基于距离的方法[9]、基于近邻的方法[10]和基于聚类的方法[11]。随着高维数据的出现,数据变得更加稀疏[6],全局离群值的挖掘受到更多不相关特征的影响,使得传统的离群点检测算法时间复杂度较高且检测效果不佳。
提出基于子空间的方法[12-13]的目的是降低高维数据出现带来的影响,此类方法将所有的数据点映射到一个或多个稀疏和低维子空间中进一步检测离群点。文献[12]提出了一种基于特征异常值相关分析的局部离群值检测算法,由于其删除了不相关数据点和数据特征,虽更适用于高维数据,但难以保证精度。文献[13]提出利用随机哈希方法对子空间内数据点进行评分。然而随着数据集规模的增长,它的复杂性迅速增加。由于基于子空间的方法面向数据点进行划分,较少地考虑数据特征间的关系,仍具有不足之处。基于特征分组的离群点检测算法有效弥补了上述缺陷。文献[7]提出基于互信息和信息熵的特征分组方法,细化了特征间相关性度量,但是该方法在检测全局离群点时忽略了不同特征分组间仍存在的关系,影响了检测效果。
近些年提出了基于数据自表示的离群点检测算法[6],此类方法时间复杂度较低,提升了高维离群点检测效率,但仍存在一些问题。文献[6]提出了基于数据自表示随机游走离群点检测方法,构建了数据点之间的稀疏表示,得到了较好的检测效果,但由于未考虑数据特征间的相关性,使其检测结果会丢失许多特征信息。文献[14]提出了一种基于数据结构信息度量的双核参数方法,获得了更加准确的数据表示结果,但此方法存在参数依赖。文献[15]提出了基于超像素的张量低秩分解,将其投影到低维空间检测离群数据。但该方法受到初始字典的约束,同时在投影过程中会丢失部分信息。文献[16]使用核范数而不是Schatten-p范数来获得更准确的数据低秩表示。以上几种方法虽有效降低了时间复杂度,但均存在参数依赖问题,同时处理高维数据时都未考虑数据特征间存在的复杂关系,从而影响了离群点检测效果。
综上所述,基于特征分组的离群点检测方法虽降低了检测维度,但在全局离群点的检测中会丢失特征分组之间的相关性信息,影响了离群点检测性能;基于数据自表示的离群点检测方法在保证检测结果准确性的同时,有效地降低了时间复杂度,但现有的数据自表示方法同样丢失高维特征包含的有效信息,离群点检测未能更全面和深入,从而影响最终的检测效果。
2 基于特征关系的数据自表示方法
该文提出的基于特征关系的数据自表示方法,结合互信息与条件熵理论来度量特征间的关联性,并将其融于数据自表示过程。互信息用于量化两个随机变量之间的依赖程度。其值越高代表两个变量之间相关性越高,一个变量在一定程度上可以被另一个变量所取代。条件熵用于描述已知在一个随机变量的条件下,另一个随机变量的不确定性。
设D={d1,d2,…,dn}为任意数据集,F={f1,f2,…,fl}为该数据集中所有特征的集合,其中:dn表示第n个数据点,fl表示第l个特征,n和l分别表示数据点和数据特征的个数。G={FG1,FG2,…,FGm}为算法FG[7]得出的特征分组集合,其中FGm表示第m个特征分组,m表示总分组数。
任一特征分组对应的数据自表示矩阵记为R={r1,r2,…,rn},以n*n方阵的形式记录了这种表示关系,其主对角线上的值(rii)为0。R由使R(ri)值最小时的ri构成,R(ri)的计算公式如下:
(1)
其中,c表示该特征分组内的特征总数,ri表示矩阵R中的第i列,FG表示该特征分组集合,FGj表示第j个特征。系数δ和ω由公式(2)和公式(5)定义。
δ用于均衡地度量特征之间的相似性与相关性,将高斯核函数用于计算特征间的距离以表示相似性,同时互信息与条件熵用于度量特征间的概率关系以表示相关性,二者结合使得特征间的复杂关系得以深入且全面的表达。δ可由如下公式得出:
(2)
其中,FGi表示第i个特征,FGj表示第j个特征,其余符号同公式(1)中定义。I(FGi,FGj)表示FGi和FGj之间的互信息,可由公式(3)得出。H(FGi|FGj)表示FGj在FGi条件下的条件熵,可由公式(4)得出。

(3)
(4)
其中,fGi和fGj表示第i和第j个特征的值。
由于具有强相关性的特征会被划分至同一分组,出现特征冗余现象,一定程度上浪费了计算资源。ω用于度量分组内特征间的冗余程度,提升了数据自表示结果的有效性。ω可由如下公式得出:
(5)
此节提出的基于特征关系的数据自表示方法,通过度量特征间存在的复杂关系,弥补了现有算法的局限性。该方法构建了数据点之间的稀疏线性组合,正常点仅由正常点表示,而离群点可以由正常点和离群点共同表示,并通过δ,ω和范数度量特征和数据的关联性,以达到将特征信息与数据信息相融合的效果。
3 融合组间数据自表示与离群点检测
根据上一节的方法,每个特征分组生成了对应的数据自表示矩阵,其中包含各分组的特征和数据分布信息,这种信息是局部的。由于不存在某个特征同时属于两个或更多分组的情况,导致数据自表示矩阵也是唯一对应的,使得原始数据被简化,造成不同矩阵中包含的离群数据信息存在差异。若直接在其基础上检测离群点所得到的结果不足以涵盖全局信息,又因为不同特征分组间仍然存在关联性,这些信息对于准确地挖掘全局离群点有帮助,进一步研究融合组间关联性将提升检测结果有效性。
3.1 基于融合组间数据自表示的计算方法
通过融合特征组间关联性构建的全局数据自表示矩阵(RT)可由如下公式得出:
(6)
其中,FG算法依据其定义的相关性度量方式,得到各组中心特征,具有与组内其余特征均强相关的特点。FG算法得出的组中心特征集表示为FC={FC1,FC2,…,FCm},RC表示FC上的数据自表示矩阵,R1·R2·…·Rm分别表示m个特征分组对应的数据自表示矩阵。公式(6)中,通过构建中心特征分组对应的数据自表示矩阵(RC),将不同组中心融合为一体,使得每个特征分组的主要信息被集中表达,均衡了组间差异性。R1·R2·…·Rm表示通过点乘各自表示矩阵,使得正常点与离群程度较大的点相互表示值与其他表示关系之间的差值增大,某些可能是离群点的数据与正常点之间的关系更弱。该文提出的基于融合组间数据自表示的计算方法,通过融合各特征分组的数据自表示矩阵,加入组间特征信息,构建全局矩阵,为后续离群点检测提供了良好的基础。
3.2 基于融合数据自表示的离群点检测算法
该文提出基于融合数据自表示的离群点检测算法,通过在构造的加权有向图上随机游走来筛选离群点。该加权有向图(S)由全局数据自表示矩阵(RT)构造得出,S中有向边为RT中数据点间的相互指向,边权值表示数据点之间的相关性,同时也表示两点之间的转移概率。S的边权值可由公式(7)得出:
(7)
其中,pxy表示数据点x到数据点y的转移概率,wxy表示图S上数据点x与数据点y之间的边权值,与pxy值相同。rxy表示RT中第x行第y列的值。
阻尼因子(η)在文献[14]中被用于马尔可夫转移概率的计算。公式(8)描述了S上不同时间的状态转移分布,随机选取初始点。
(8)
其中,S(t)表示t时刻的状态转移分布,P表示转移概率矩阵,O表示1*n的矩阵,n表示数据点个数。
基于稳定后的状态转移分布,通过公式(9)得出每个数据点的异常因子(od),其用于描述数据点的离群程度。正常点被转移到的概率较高,而离群点被转移到的概率较低,取异常因子最小的h个点作为最终的全局离群点。
(9)

综上所述,基于融合数据自表示的离群点检测算法基本思想为:首先在FG算法的特征分组结果基础上,使用公式(1)构建每个分组和组中心特征集对应的数据自表示矩阵;然后,使用基于融合组间数据自表示的计算方法得出全局自表示;最后,在加权有向图上使用马尔可夫随机游走检测离群点。其算法描述如下:
算法1:MDSR(An outlier detection algorithm based on mergence data self-representation)
输入:FG算法得出的特征分组:G={FG1,FG2,…,FGm},组中心特征集为FC={FC1,FC2,…,FCm}
输出:异常因子(od)
1.根据公式(1),得出G中每个特征分组和FC对应的数据自表示矩阵(R)
2.根据公式(6),构建全局数据自表示矩阵(RT)
3.根据公式(7),使用RT计算出状态转移矩阵(P)
4.η⟸0.1,S(0)⟸{1/n,1/n,…,1/n}
5.根据公式(8),得出稳定的状态转移分布(S(t))
6.根据公式(9),计算出每个数据点的异常因子(od),并取其值最小的h个点作为最终的全局离群点。
4 实验分析
4.1 实验设置及环境
为了验证MDSR算法的有效性,在人工数据集和真实数据集上共同实验,使用LOF[17],SOD[18],ROD[19],COPOD[20]和R-GRAPH[6]作为对比算法,采用ROC曲线下面积(AUC)和运行时间作为评价指标。真实数据集包含3个UCI Machine Learning Repository(UCI)数据集和6个Outlier Detection DataSets(ODDS)数据集,详见表1。
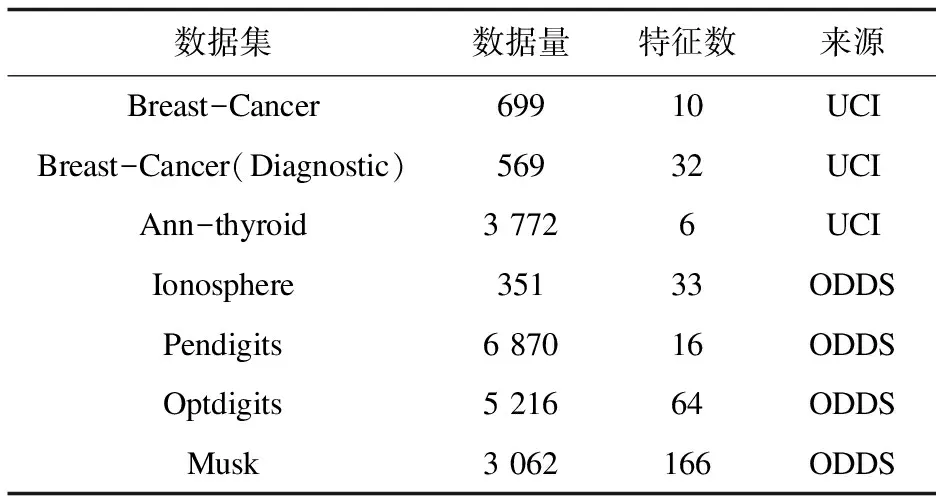
表1 真实数据集
人工数据集来源于文献[21],使用文献[8]中对人工数据集的处理方法,得到本实验中的28个数据集,分别为:18个数据规模一定的数据集,其中特征数量包含20,30,40,50,75和100,每个特征数量中包含3个不同的数据集;与10个特征数量一定的数据集,其中特征数为20,数据量从1 000到10 000,详见表2。该文基于Matlab平台,AMD Ryzen 7 4800H 2.90 GHz CPU和RTX 2060 GPU实现了MDSR算法。

表2 人工数据集
4.2 人工数据集实验结果分析
6种算法在6个不同维度人工数据集上的AUC如图1所示,具体AUC数值如表3所示,取每维度中的3个数据集上最大的AUC作为实验结果。依据参考文献[8,22],LOF和SOD算法中参数n_neighbors的值取5时其算法模型达到最优。

图1 人工数据集上的AUC对比

表3 人工数据集上的AUC数值
从图1和表3可见,对于所有维度的人工数据集,MDSR算法的AUC值明显比LOF,SOD,ROD和COPOD算法的高,较好地完成了离群点检测任务。
LOF和ROD算法性能随着数据维度的增加而大幅下降,造成这种现象的原因是,即使ROD算法提出了基于全维3D子空间的方法,它们仍然都在全局数据中直接检测离群值,当处理高维数据时,对于LOF和ROD算法将更难检测离群值。COPOD算法AUC值则在小范围内浮动,是因为它更多受到数据分布的影响,而非特征的数量。SOD算法构造的子空间中包含冗余特征,数据特征越多,冗余程度越大,导致SOD同样难以有效处理高维数据。提出的MDSR算法的AUC值比R-GRAPH的略高,是因为MDSR不仅考虑了特征冗余问题还将特征间复杂的关联性融于数据自表示的过程中,而R-GRAPH在其数据自表示过程中并未关注这些问题。因此MDSR算法性能不会随着特征数的增加而显著降低,从而保证其面对高维数据的离群点检测任务时,仍可以得到较准确的检测结果。
离群点检测算法的运行时间是衡量其检测效率的一个重要评价指标。各算法在人工数据集上的运行时间对比如表4所示。

表4 不同特征数量人工数据集上的运行时间对比 s
从表4可见,MDSR算法在前3个数据集上的运行时间比SOD算法的少,在全部数据集上的运行时间比ROD算法的少。对于SOD算法,选择相关子空间的过程占用了运行时间。对于ROD算法,构建全局三维子空间的过程有较大的时间开销。由于COPOD算法是基于连接的,在数据集规模为1 000的前提下,其运行时间浮动较小。提出的MDSR算法深入挖掘特征关系,随着数据特征的增加,这种复杂关系更加难以计算,导致该方法在运行时间上略有增加。为分析数据规模对MDSR算法运行时间的影响,在数据集D20_1,D20_2,…,D20_10上进一步对比,结果如表5所示。

表5 不同数据量人工数据集上的运行时间对比 s
从表5可见,实验中所有算法的运行时间都随数据量增加而线性增加,但MDSR算法的运行时间仍保持在较低值,且远小于SOD和ROD算法的运行时间,更直观的对比如图2所示。
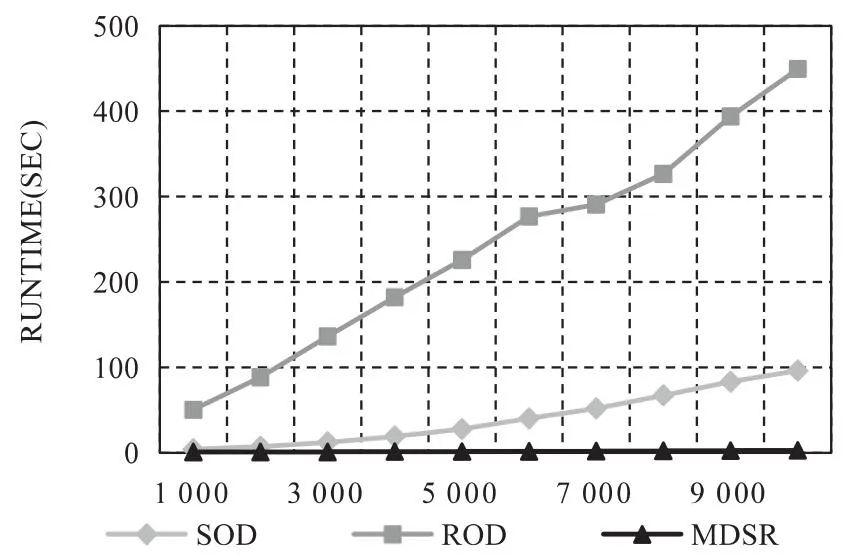
图2 不同数据规模下SOD,ROD和MDSR算法运行时间对比
由于MDSR算法考虑了特征间关联性,使其运行时间比COPOD和R-GRAPH算法的较长。但是结合表3中AUC数值和表4、表5中运行时间可以得出,该文提出的算法运行时间虽不是最短,但仍取得了最好的检测结果,同时结合数据量大小和数据维度对MDSR算法性能的影响,表明该算法适合用于高维离群点检测任务且总体优于对比算法。
4.3 真实数据集实验结果分析
为进一步验证MDSR算法的有效性,将其与LOF,SOD,ROD,COPOD和R-GRAPH在9个真实数据集上进行了对比实验,且设置了3种离群点占比,分别为2%,5%和10%。由于Pendigits,Optdigits,Musk和Speech数据集中离群点占比不足5%,故只以2%的离群值作为实验设置。3种离群点占比下不同算法在真实数据集上的AUC对比如表6所示。

表6 真实数据集上的AUC对比
从表6可见,MDSR算法具有较好的检测结果。结合表1,MDSR算法无论在较低维数据集Breast Cancer和Ionosphere上,还是在较高维数据集Musk,Arrhythmia和Speech上,AUC值都明显比LOF,SOD和ROD算法的高。由于LOF算法原理较为直接和单一,导致其在高维数据集上无法保证检测效果。MDSR算法考虑了特征间关系和数据信息的融合,优于仅研究特征信息的SOD算法,使得MDSR算法的检测结果更突出。对于ROD算法,从表6可见其AUC值大于0.7,只出现在低维数据集Breast-Cancer(Diagnostic)和Ionosphere上。由于ROD在检测过程中旋转其构建的3D子空间,此过程需要占用的内存随数据维度增加而变大,而本设备不足以支撑ROD算法检测高维数据集Arrhythmia和Speech。MDSR算法的AUC值相比R-GRAPH的略优,原因是R-GRAPH只通过研究数据间相互表示关系检测离群点,存在一定的局限性。对于基于数据连接的离群点检测算法(COPOD),当数据量小于1 000时,它的检测AUC可以达到0.9以上,但数据量一旦超过3 000,其检测AUC下降幅度超过了0.3。
结合以上分析可以得出,MDSR算法更加全面和深入地挖掘了数据和特征信息,具有较好的稳定性和泛化性。
各算法在真实数据集上的运行时间对比如表7所示。
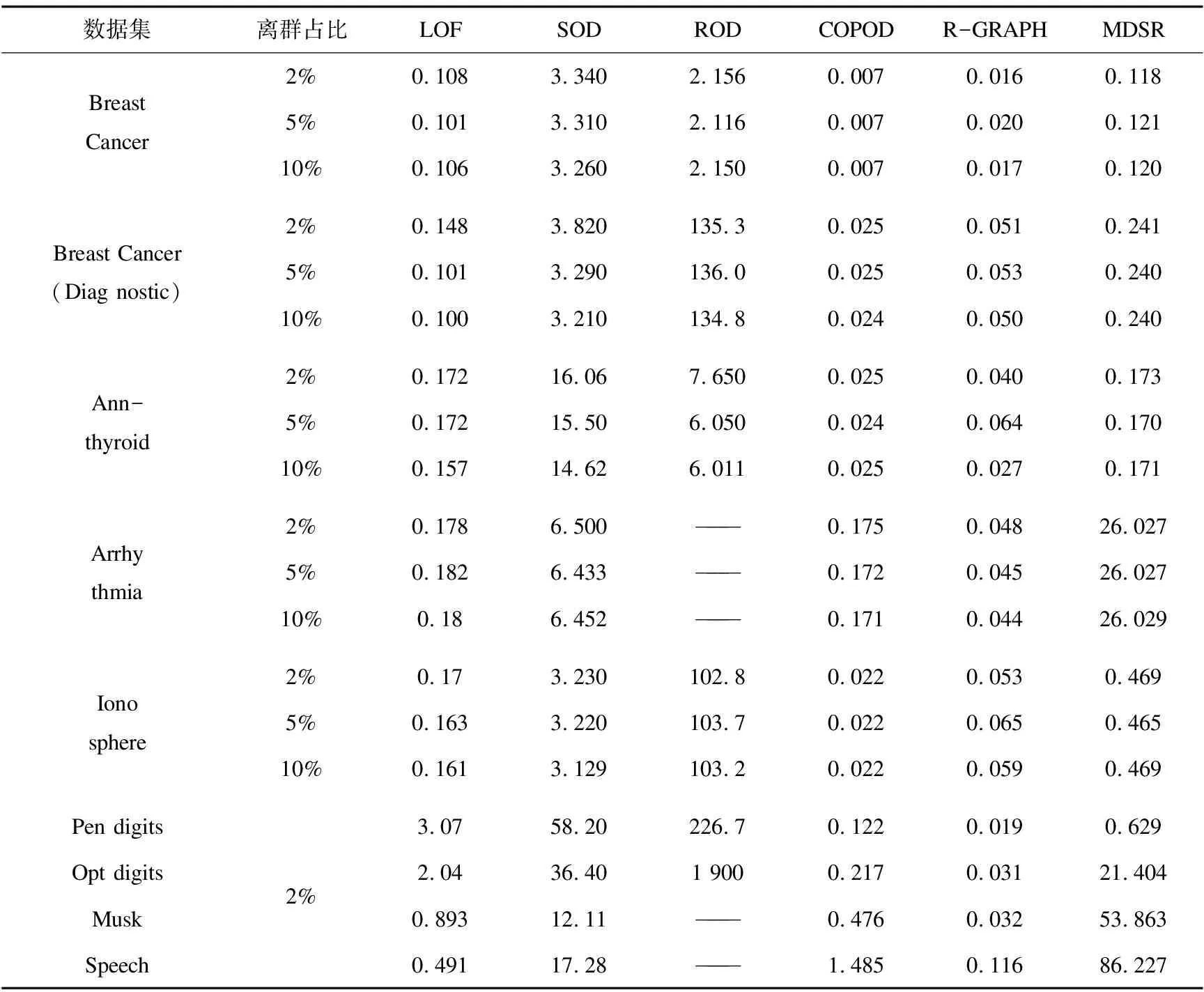
表7 真实数据集上的运行时间对比 s
从表7可见,MDSR算法的运行时间在所有数据集上少于SOD和ROD算法的运行时间,而只在较低维数据集上少于LOF算法的运行时间。SOD算法将时间消耗在寻找子空间上,ROD算法则在构造三维子空间和旋转检测上花费较多时间,导致其运行时间随着数据特征的增多大幅上升。虽然COPOD算法运行时间较短,但该算法并不能保证离群点检测效果。MDSR算法需要较多的时间用于计算特征间关联性,但为了能在高维数据中更有效地挖掘出离群点,可以忽略这部分时间开销。
5 结束语
通过均衡地度量特征与数据关联,该文提出一种基于融合数据自表示的离群点检测算法,充分挖掘并体现了数据特征间和数据间的复杂关系,有效改善了高维离群点检测性能,适用于高维数据的离群点检测任务。算法度量特征间相关性的过程较为费时,下一步主要研究工作是采取一些方法来优化该过程,已在保证检测有效性的基础上降低其时间消耗。
