Singularity of Two Kinds of Four Cycle Graphs

-,-,,-

(1. School of Mathematics and Statistics, Qinghai Minzu University, Xining 810007, China; 2. School of Mathematics and Statistics, Qinghai Normal University, Xining 810008, China)

Abstract: Let G be a finite simple graph and A(G) be its adjacency matrix.Then G is singular if A(G) is singular.The graph obtained by bonding the starting vertices and ending vertices of three paths Pa1,Pa2,Pa3 is called θ-graph, represented by θ(a1,a2,a3).The graph obtained by bonding the two end vertices of the path Ps to the vertices of the θ(a1,a2,a3) and θ(b1,b2,b3) of degree three, respectively,is denoted by α(a1,a2,a3,s,b1,b2,b3) and called α-graph. β-graph is denoted when β(a1,a2,a3,b1,b2,b3)=α(a1,a2,a3,1,b1,b2,b3).In this paper, we give the necessary and sufficient conditions for the singularity of α-graph and β-graph, and prove that the probability that a random given α-graph and β-graph is a singular graph is equal to and , respectively.

Keywords: Adjacency matrix; Singular graph; Nullity; Probability

§1.Introduction

LetGbe a finite undirected simple graph with vertex setV(G)={1,2,...,n}.The adjacency matrix ofGis defined to be ann×nmatrixA(G)=(aij),

wherei∼jrepresents the verticesiandjare adjacent.Obviously,A(G) is a real symmetric matrix with diagonal elements 0, and its eigenvalues are all real numbers.The eigenvalues ofA(G) are also the eigenvalues ofGand form the spectrum ofG.The number of non-zero eigenvalues and zero eigenvalues in the spectrum ofGare called therankand thenullityofG, respectively, and are denoted byr(G) andη(G).Apparentlyr(G)+η(G)=n.ThenGissingularifA(G) is a singular matrix.In other words,Gis singular if and only if 0 is an eigenvalue ofG.

The nullity (or rank) of a molecular graph has many important applications in chemistry[5–8,10,27]; for example, a conjugated hydrocarbon molecule can be represented by molecular graph and the necessary condition for the stability of molecular chemical properties is that the nullity of the molecular graph is zero [6].Collatz and Sinogowitz in 1957 [5] proposed the problem of characterizing all graphs with the nullity greater than zero (the problem of characterizing all singular graphs).However, limited and special results are obtained for this problem [2,3,11,12,18,20–23,26] so far.Many researchers have studied the relationship between the nullity of a graph and its structure [4,9,13,14,19].Singular graphs are also related to the representation theory of finite groups, combinatorial mathematics, algebraic geometry and other fields [1,17,24,25].Recently, we give the necessity and sufficiency of the singular of some classes tricycle graphs and probability of the occurence of these singular graphs [15,16].In this paper,we study the singularity of two kinds of the four cycle graphs.

LetPn,CnandKndenote the path, cycle and complete graph withnvertices, respectively.θ(a1,a2,a3) is theθ-graph formed by bonding the starting vertices and the ending vertices of three pathsPa1,Pa2,Pa3, respectively, whereai ≥2(i=1,2,3) and at most one ofaiis 2.The graph obtained by bonding the two end vertices of the pathPsto the vertices of theθ(a1,a2,a3)andθ(b1,b2,b3) of degree three, respectively, is recorded asα(a1,a2,a3,s,b1,b2,b3)(see Figure 1),which is calledα- graph.Denotedβ(a1,a2,a3,b1,b2,b3)=α(a1,a2,a3,1,b1,b2,b3)(see Figure 2),which is calledβ- graph.

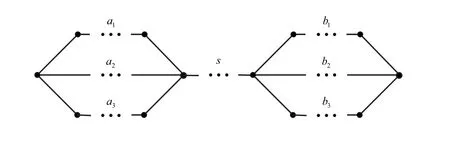
Fig.1 Graph α(a1,a2,a3,s,b1,b2,b3).

Fig.2 Graph β(a1,a2,a3,b1,b2,b3).

LetG∪Hbe the union of two graphsGandH.Ois the set of odd numbers ofa1,a2,a3,b1,b2,b3.The vertex of degree 1 is called the pendant vertex, and the vertex adjacent to the pendant vertex is called the quasi-pendant vertex.For the notations and terms which are not defined above, please refer to [6].

A path with the odd number of vertices is called aodd path, and a path with the even same as above is calledeven path.These paths constitute the twoθ-graphs in theα-graph.The main conclusions are the two theorems below.

Theorem 1.1.G=α(a1,a2,a3,s,b1,b2,b3)is singular if and only if one of the following holds.

(a)|O|=0,s is odd.

(b)|O|=1,s is even,and the length of the cycle which consists by two even paths in the θ-graph is a multiple of 4.

(c)|O|=2,(i)two odd paths are in one θ-graph,(1)s is odd,(2)s is even,and the length of the cycle formed by two odd paths is a multiple of 4;(ii)Two odd paths are in two θ-graphs respectively,s is odd,and the length of two odd cycles is4s+1-type,the other two is4s+3-type,in the four odd cycles in α graph.

(d)|O|=3,(i)three odd paths are in one θ-graph;(ii)Three odd paths are in two θ-graphs,(1)s is odd,the length of the cycle formed by two odd paths is a multiple of 4,(2)s is even,the length of the cycle formed by two odd paths is a multiple of 4 or the length of the cycle formed by two even paths is a multiple of 4.

(e)|O|=4,(i)s is odd;(ii)s is even,(1)three of the four odd paths are in a θ-graph,(2)there are two odd paths in each θ-graph,and the length of at least one of the two cycles which formed by four odd paths is a multiple of 4.

(f)|O|≥5.

By theorem 1.1, the following corollary 1.1 is obvious.

Corollary 1.1.G=β(a1,a2,a3,b1,b2,b3)(see Figure 2)is singular if and only if one of the following holds.

(i)|O|=0,4,5,6.

(ii)|O|=2,(1)Two odd paths are in one θ-graph;(2)Two odd paths are in two θ-graphs respectively,and the length of two odd cycles is4s+1-type,the other two is4s+3-type,in the four odd cycles in β-graph.

(iii)|O|=3,(1)Three odd paths are in one θ-graph;(2)Three odd paths are in two θ-graphs,and the length of the cycle formed by two odd paths is a multiple of 4.

§2.Several lemmas

Lemma 2.2.[3]If G has a pendant vertex,graph H is obtained by deleting the pendant vertex and the quasi-pendant vertex adjacent to it from graph G,then η(G)=η(H).Equivalently,G is non-singular if and only if H is non-singular.

§3.Proof of the principal theorem

3.1.Proof of Theorem 1.1

|V(G)|=a1+a2+a3+b1+b2+b3+s-10.Combine the parity of the 7 paths and the symmetry of graphα(a1,a2,a3,s,b1,b2,b3), we will discuss as follows.

Case 1|O|=0.

By Lemma 2.3,Gis singular if and only if

but it is impossible to hold.SoGis non-singular.

Ifsis odd,Gdoes not have a spanning Sachs subgraph, soGis singular.

Case 2|O|=1.

Ifsis even, we assumea1is an odd number.The spanning Sachs subgraphs of graphGwith two cycles have:

but this is impossible to hold.SoGis non-singular.

Case 3|O|=2.

Whensis even number and two odd paths are concentrated in oneθ-graph.We can assume thata1,a2are odd numbers.The spanning Sachs subgraphs of graphGwith two cycles have:

but this is impossible to hold.SoGis non-singular.

Whensis odd and two odd paths are concentrated in oneθ-graph.We can assume thata1,a2are odd numbers.Ghas no spanning Sachs subgraph,Gis singular.

Whensis odd and two odd paths are distributed in twoθ-graphs.We can assume thata1,b1are odd numbers.There is no the spanning Sachs subgraph with two cycles.The spanning Sachs subgraphs with a cycle have:

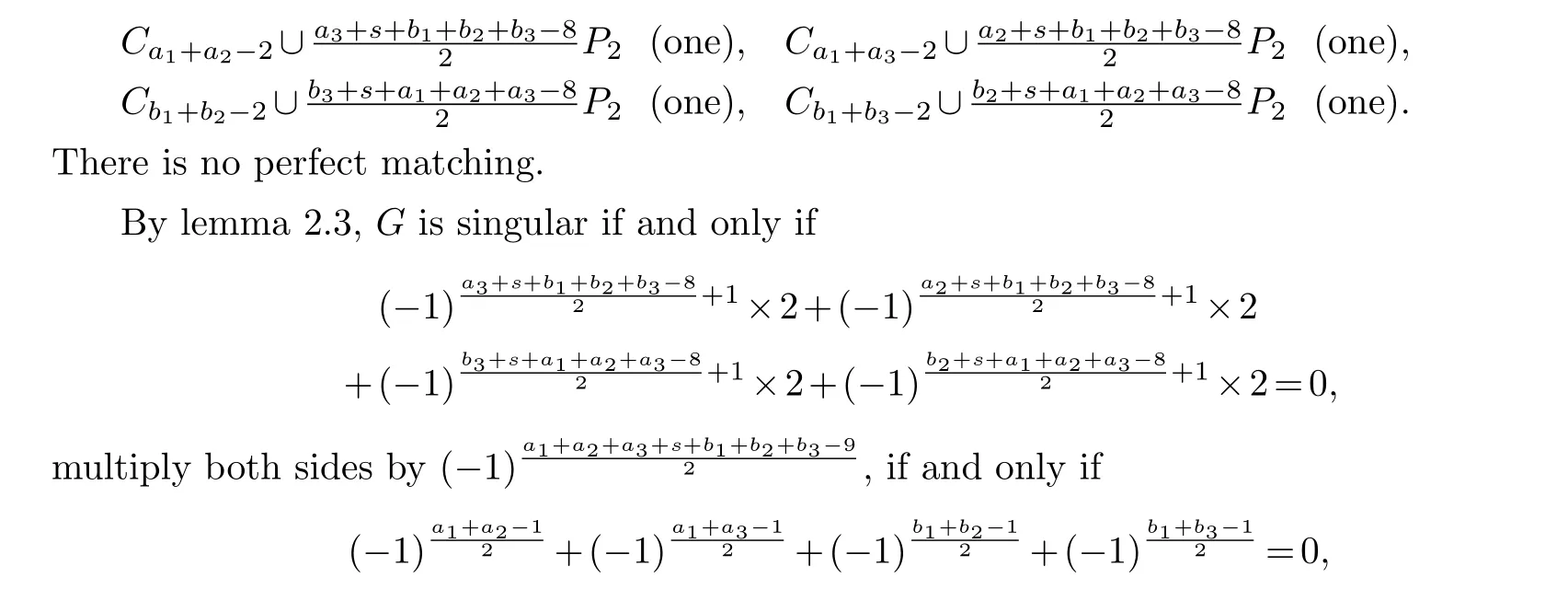
by Lemma 2.4, if and only if the length of two odd cycles is 4s+1-type, the other two is 4s+3-type, in the four odd cyclesCa1+a2-2,Ca1+a3-2,Cb1+b2-2,Cb1+b3-2in theGgraph.

Case 4|O|=3.

Whensis even and three odd paths are concentrated in oneθ-graph.We can assume thata1,a2,a3are odd numbers.Ghas no spanning Sachs subgraph,Gis singular.

Whensis even and three odd paths are distributed in twoθ-graphs.We can assume thata1,a2,b1are odd numbers.The spanning Sachs subgraphs of graphGwith two cycles have:

Whensis odd and three odd paths are concentrated in oneθ-graph.We can assume thata1,a2,a3are odd numbers.Ghas no spanning Sachs subgraph,Gis singular.

Case 5|O|=4.

Whensis even and there are three of four odd paths are concentrated in oneθ-graph.We can assume thata1,a2,a3,b1are odd numbers.Ghas no spanning Sachs subgraph,Gis singular.

Whensis even and there are two odd paths in each of the twoθ-graphs.We can assume thata1,a2,b1,b2are odd numbers.The spanning Sachs subgraphs of graphGwith two cycles have:

Whensis odd and there are three of four odd paths are concentrated in oneθ-graph.We can assume thata1,a2,a3,b1are odd numbers.Ghas no spanning Sachs subgraph,Gis singular.

Whensis odd and there are two odd paths in each of the twoθ-graphs.We can assume thata1,a2,b1,b2are odd numbers.Ghas no spanning Sachs subgraph,Gis singular.

Case 6When|O|=5 or|O|=6,whethersis even or odd,Ghas no spanning Sachs subgraph,Gis singular.

3.2.Proof of Theorem 1.2

For convenience,Xrepresents the random event:G=α(a1,a2,a3,s,b1,b2,b3) is a singular graph,Yrepresents the random event:G=β(a1,a2,a3,b1,b2,b3) is a singular graph.p(X)represents the probability that eventXoccurs.By the full probability formula

wherep(A|W) represents the probability that eventAoccurs under the condition that eventWoccurs.Since