Harvesting in a Toxic Predator-Prey Model with Carrying Capacity and Maturation Double Delays

,-

(College of Mathematics and Statistics, Guangxi Normal University, Guilin 541006, China)

Abstract: In this paper, a model of predator-prey with dual delay in maturation and carrying capacity is discussed, in which the past activity of the prey should have an impact on the carrying capacity, the mature prey initiates defense mechanisms to release toxins when subjected to predation, and a commercial harvest of the prey is performed.The stability of the equilibrium of the system in the absence of delay is examined and the optimal harvesting strategy of the model is proven.By investigating the roots of the characteristic equation and applying normalized theory, the properties of the coexistence equilibrium of the system and the conditions for the occurrence of the Hopf bifurcation in the neighborhood of the positive equilibrium are described for various combinations of delays.In the end, numerical simulations are used to verify theoretical analysis results.

Keywords: Predator-prey; Time delay; Hopf bifurcation; Harvesting; Toxicant

§1.Introduction

There is a population relationship in nature that is both interdependent and mutually constraining.PopulationAfeeds on populationB, and populationBsurvives on abundant natural resources,which is ecologically called populationAas predator and populationBas prey,and they form a predator-prey system.Snail kites-snails, sharks-edible fish, pandas-bamboo,anteaters-ants, and so on are classic examples of predator-prey models.The dynamical system of the predator-prey model has been extensively studied [15,22,31].In the predator-prey model,when subjected to predation by a predator, the prey activates defense mechanisms to reduce the danger of predation.The genres of defense mechanisms are group defense,fake death,camouflage,chemical and physical defense, etc.The literature [7,14,26] explored predator-prey models with group defense mechanisms.In addition, some researchers have investigated the reduction of predation risk by prey through the release of chemicals, such as Roy [27] examined the effects of toxin-producing phytoplankton on the dynamics of other phytoplankton and zooplankton.The article [18] discusses a predator-prey model in which prey protect themselves by releasing toxins, and the research results show that toxic substances released by prey (phytoplankton)can effectively control the growth of harmful algal blooms.Stenaptinus insignis releases venom to attack predators when in danger, resulting in the growth inhibition of predators [6].

In ecological communities, the rate of population variation depends not only on the present state but also on the past activities of the species, and this issue is addressed by introducing a delay.Several ecological mathematicians have analyzed predator-prey models with delays.Mukhopadhyay et al.[21] considered that the poisonous substances produced by a species against another species are not transient but have a maturation lag, i.e., the species releases its toxins only after reaching adulthood.Pal et al.[23] explored two competing fish species that deter competition for natural resources by freeing toxic substances from one another, where one species only produces toxic substances after maturity.On the other hand, the carrying capacity of a species is the maximum number of populations that the environment can sustain, and it may be altered by factors such as changes in the environment or the activities of the species.For instance, technological advances can improve the carrying capacity of a species [20,28,29],whereas factors like pollution of the environment, depletion of resources, and the occurrence of diseases can reduce the carrying capacity of species [8].The carrying capacity proportional to population density or biological resources has been proposed in the literature [16,17,30],respectively.Pati and Ghosh posed a predator-prey model with delayed carrying capacity and showed that the stability of the system at extraordinary equilibrium points is altered by delay [24].Populations may be affected by multiple time delays simultaneously during growth.For instance, Jiang et al.[11] investigated the existence of branches of the Leslie-Gower predator-prey model with two delays.Yuan et al.[34] studied a predator-prey model with two different time delays and obtained the exact bifurcation point using the delay as the branching parameter.More references are available at [19,35].

As socio-economic growth and overfishing by humans have damaged natural resources, it is more practical to consider predator-prey systems with trapping terms from the perspective of biological resources and economic theory [2,5,12,13].Selective harvesting of fish of a given age or size plays a vital role in modulating ecosystems, and several researchers have addressed the conjunctive dynamic effects of having a catch and a time lag on the system [10,32,33].

As far as the current state of research is concerned, relatively few articles still investigate the carrying capacity with delay.In this paper,we focus on extending the model of the literature[24],which does not consider realistic capture and does not take into account the defensive behavior of the prey.When fishermen engage in fishing operations, the small fish caught are thrown back into the sea, so they usually choose nets with slightly larger mesh to catch fish, and the small fish will return to the sea through the mesh to continue their survival, leaving larger fish behind.Accordingly, in this work, we introduce a harvest term with a maturation lag and assume that the prey will not release toxins to the predator until after maturation.

The structure of this paper is as follows.In Section 2 the mathematical model is constructed and analyzed.Section 3 has considered the stability of the proposed equilibrium and the optimal harvesting strategy in the absence of delay.The delayed system is discussed in Section 4.Section 5 runs numerical simulations to test the findings of the theoretical analysis.

§2.Formulation of mathematical models

In this contribution, we would like to extend the mathematical model in the literature [24].It is assumed that mature prey, when subjected to predation, will release toxins to the predator,thus inhibiting the growth of the predator, and therefore a delay is added to the toxin infection term of the predator.In the other case, we assume that the prey of a given size is captured intentionally, so we add the delay of maturity to the harvest term.Based on the previous assumptions, we yield the following delay differential equation

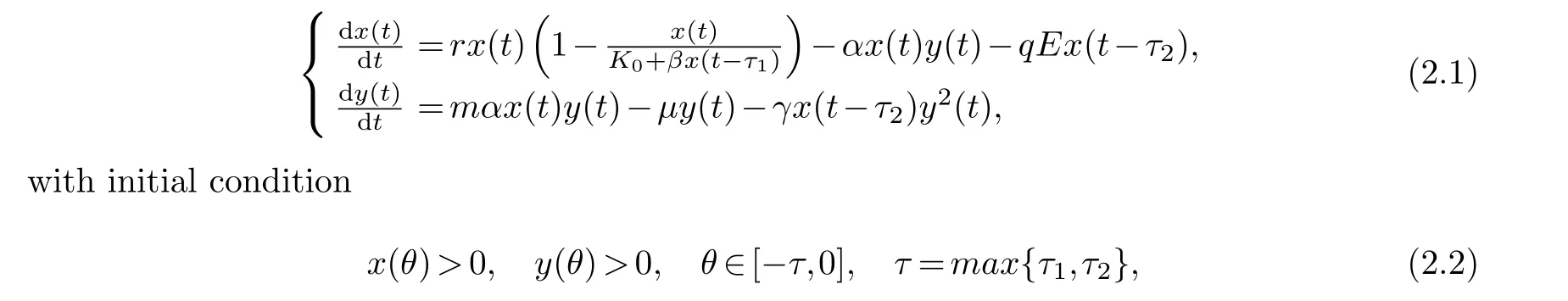
in whichx(t),y(t) indicates the population density of prey and predator at timet, respectively,rdenotes the natural growth rate of prey,K0is the inherent carrying capacity of populationx,βx(t-τ1) is the effect of past activities of prey populations on the carrying capacity, parameterβ ∈R, and whenβ>0 (resp.<0), the past activities of the species are productive (resp.destru-ctive),αstands for the rate of predator consumption of prey,qis the coefficient of the allowable catch,Eshows the fishing effort,mmeans the conversion rate,µis the mortality rate of predators, andγis the coefficient of toxicity.

Theorem 2.1.Solutions of the system(2.1)with original data(2.2)are positive with t≥0.

By applying (2.3) and (2.4), whenβ<1, we obtained

§3.Analysis of model without delay

3.1.Analysis of the local stability of the equilibrium

When the delays do not exist, i.e.τ1=τ2=0, the DDE (2.1) becomes

at any equilibrium (xe,ye).

(i) ForP0(0,0), the characteristic equation is (r-qE-λ)(-µ-λ)=0, and its characteristic roots areλ1=r-qE,λ2=-µ<0.Thus, the locally asymptotically stable node atP0(0,0) whenrqE.

(ii) ForP1, the characteristic equation is

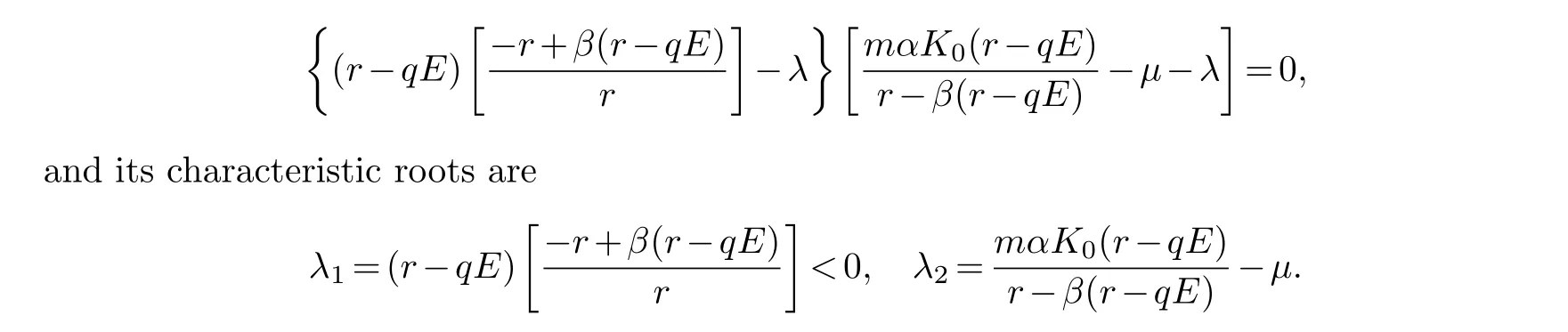
To makeλ2<0 there must be conditions (mαK0+µβ)(r-qE)<µr.So, the locally asymptotically stable node atP1when (mαK0+µβ)(r-qE)<µr.

(iii) ForP2, the characteristic equation is

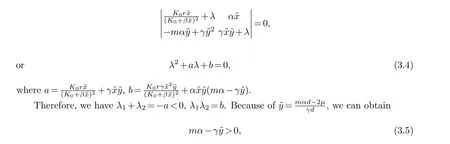
hence we can getb>0 whenτ1=τ2=0, all eigenvalues of the characteristic equation have negative real parts.We can draw the conclusion thatP2is a locally asymptotically stable node.

3.2.Bioeconomic equilibrium

The economic profit is positive whenpqx>c, at which time the prey is harvested.From(3.7) to (3.9), one can get the bioeconomic equilibrium,

3.3.Optimal harvesting strategy

From the economic and political point of view, the optimal harvesting policy is to maximize the economic profit sustainably.Using Pontryagin’s maximum principle [25] to explore the optimal harvesting strategy, the target is to maximizeJsubject to the state (3.1).Now consider the present value of the returns of the continuous-time stream

in whichδis the instantaneous annual discount rate,π(x,y,E,t)=(pqx-c)E.In the following we build the Hamiltonian function

Among them,ρ1(t) andρ2(t) are the adjoint variables andEis the optimal control, which is located in the control interval [0,Emax], andEmaxis the maximum feasible harvest.Letσ(t)=e-δt(pqx-c)-ρ1qxbe the switching function, and since the Hamiltonian function is a linear function of the adjoint variables, the optimal control must be a mixture of Bang-Bang control and singular control.

In Bang-Bang control, the optimal harvesting strategy of must satisfies the following conditions

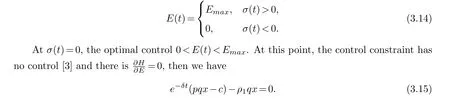
whereM2=-αxpqE, it can be clearly demonstrated that the shadow priceρi(t)eδt,i=(1,2) is bounded whent→0.Taking the values ofρ1(t)andρ2(t)from(3.23)and(3.24)and substituting them into (3.15), we obtain

now, taking into account the optimal equilibrium solution of the above issue, from the first equation of the model (3.1) we get

§4.Analysis of model with delay

In this section, we investigate the dynamic effects of time delays on the stability of the coexistence equilibrium by examining models with carrying capacity and maturation time delays.The characteristic equation of the system (2.1) at any equilibrium (xe,ye) is

then (4.3) is equal to the characteristic equation (3.4) of the without delay model, and it was derived from the previous analysis that the eigenvalues have a negative real part when and only when (H1):a1+a3+a5>0 anda2+a4+a6>0.

Case 4.2:τ1>0,τ2=0, the characteristic equation turns into

It is possible that the delay may cause a shift in the stability of the coexisting equilibrium.The stability changes only through the Hopf branch, and the system has a pair of purely imaginary roots for the eigenvalues whenτmeets a critical value.Then, it follows that there existsω>0 such thatλ=iωis a root of the (4.4), and using the Euler transform, separating the real and imaginary parts, we can introduce

(H2): (a1+a5)2-2(a4+a6)-a23>0, (a4+a6)2-a22>0.

If (H2) is valid, then the (4.6) has no positive roots andωdoes not exist.As such, when(H1) and (H2) were established,P2is a locally asymptotically stable node.

(H3): (a4+a6)2-a22<0 holds.

Then it follows that(4.6)has at least one positive root based on the Routh-Hurwitz criterion,and thus (4.6) has a pair of purely imaginary roots±iω1.Dissolvingsin(ωτ1) from (4.5), we can find by calculation thatτ1kcorresponding toω1is equal to

wherek=0,1,2,....

Next, letλ=iω1be the root of the (4.6), (4.4) is differentiated with respect toτ1and can be derived as

(iv) Since

where

in the next step, we define

Since (4.13) is a transcendental equation, it is difficult to study the nature of its roots,so the dynamical behavior of system (2.1) is examined by considering the existence of Hopf bifurcation in the vicinity of equilibrium.It is trivial to demonstrate that when (4.13) has at least two positive and single roots 0<ω10<ω11<..., (4.10) has at least one pair of purely imaginary roots.Subsequently, by makingω1c=max{ω1k,k=0,1,2...}, we can introduce the corresponding critical valueτ1c

It follows to decide on the transversality condition for the existence of Hopf bifurcation,which is defined as the presence of at least one pair of purely imaginary roots whenτreaches a critical value, (4.10) differentiates forτ1, which gives

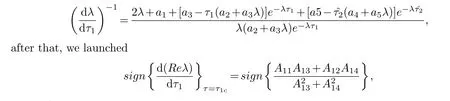
whereA1k,k=1,2,3,4 meets the following

(H6):A11A13+A12A14>0.

Theorem 4.3.If(H1)and(H6)are satifies, ˆτ2∈(0,τ20),we can come to the conclusion that P2is a locally asymptotically stable node if τ1<τ1c,and P2is unstable if τ1>τ1c,system(2.1)goes through the Hopf-bifurcation at τ1=τ1c.

Case 4.5:τ1∈(0,τ10),τ2>0,τ1/=τ2.

In this subsection,τ2is used as a bifurcation parameter andτ1= ˆτ1is a fixed value within the stability interval (0,τ10).By comparing with the symmetric analysis of case 4.4, we can receive the following equation:

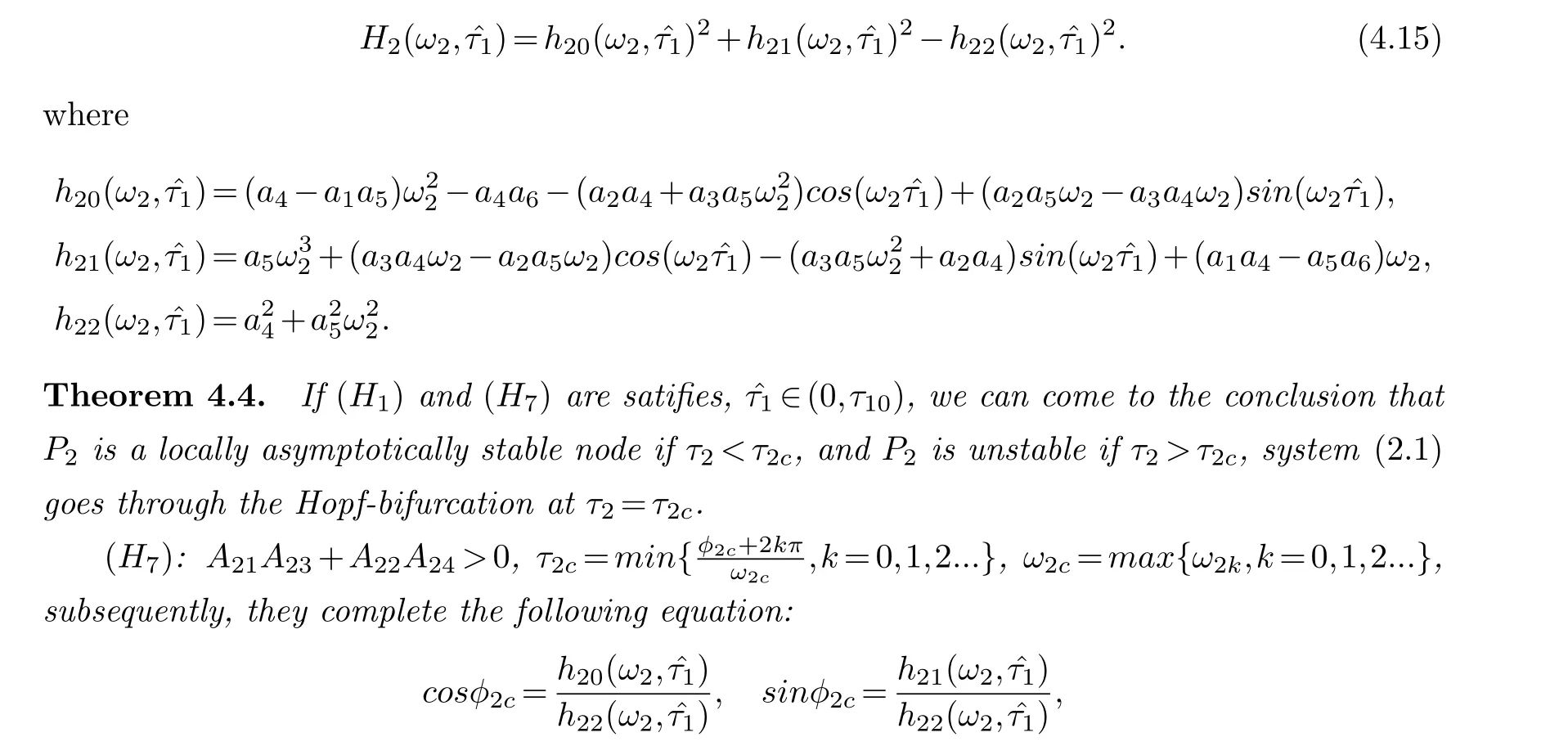
Where

§5.Numerical simulation

The main purpose of this subsection is to check the findings of the theoretical analysis by numerical simulation.

Example 5.1.We select the appropriate data to assign to the parameter values,r=0.5,K0=20,µ=0.03,q=0.05,E=1,α=0.2,m=0.4,γ=0.005,β=-2.Table 1 describes the eigenvalues as well as the properties of these equilibria,and they are verified in Fig.1 using Matlab.This is consistent with the conclusion of Theorem3.1.

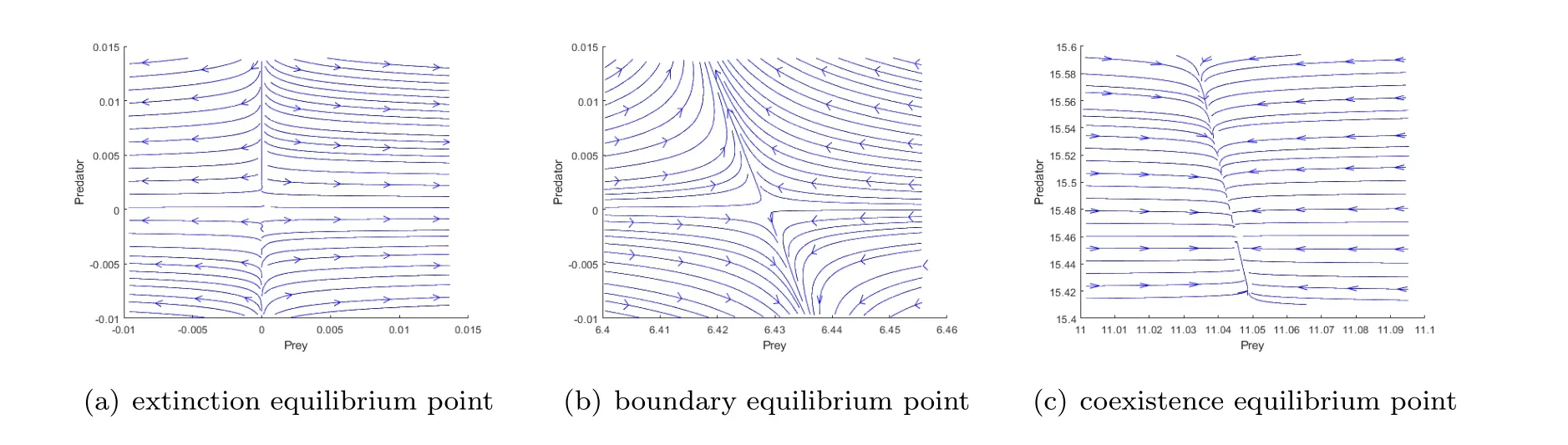
Fig.1 Delay-free system phase diagram.

Table 1 Eigenvalues of equilibrium points and their properties.

Example 5.2.We set the parameter values as r=0.9547,K0=40,µ=0.0025,qE=0.6302,α=0.1053,m=0.9907,γ=0.0801,β=-15.158.We can calculate the equilibrium(˜x,˜y)≈(1.9793,1.2866).We have a1+a3+a5≈0.9603>0,a2+a4+a6≈0.1546>0.

Case(a):τ1=τ2=0,the equilibrium is stable in this case,the variation diagram of the equilibrium is presented in Fig.2.Subsequently,we will discuss the following categories.locally asymptotically stable,then when τ1=3.58>τ10≈3.5695,the equilibrium is unstable.As shown in Fig.3.

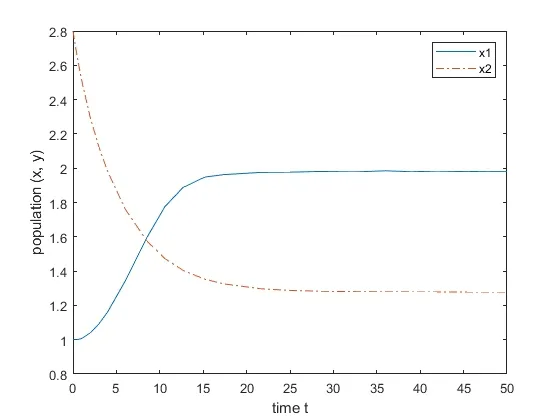
Fig.2 The variation of the equilibrium point when τ1=τ2=0.

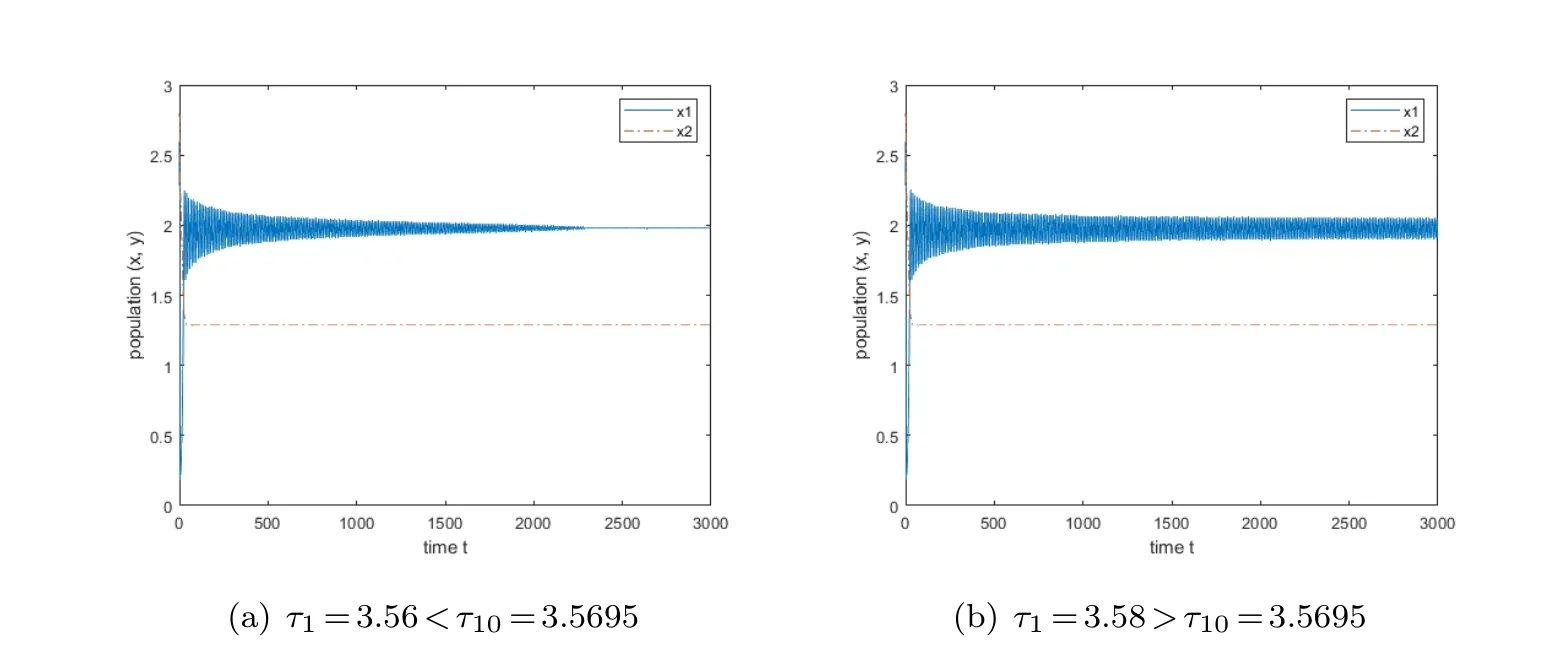
Fig.3 The variation of the equilibrium point when τ1>0 and τ2=0.

Case(d):When τ1is considered as a parameter,and τ2is fixed to τ2=2.3,which is chosen within the stability interval(0,2.8930).Performing the calculation yields ω1c ≈0.7877,τ1c ≈0.3232,after that,when we set τ1=0.31,the coexistence equilibrium is stable,and when we make τ1=0.33,the stability of the coexistence equilibrium is violated.Its results are illustrated in Fig.5.

Case(e):When τ2is viewed as a parameter,τ1is fastened to τ1=2,which is picked in the stability interval(0,3.5695).Carrying out the calculation yields ω2c ≈0.8857,τ2c ≈0.6195,after which the coexistence equilibrium is stable when we set τ2=0.60,while the stability of the coexistence equilibrium is violated when we make τ2=0.62.The outcomes are shown in Fig.6.

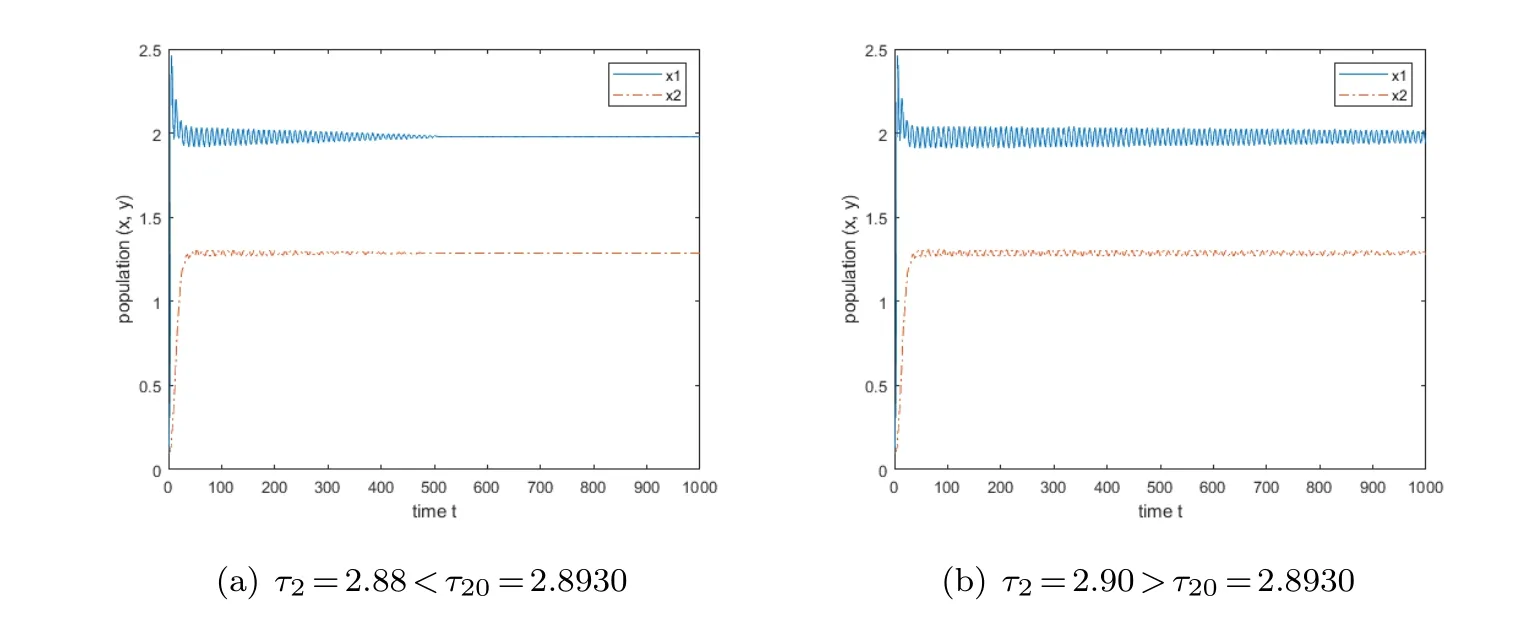
Fig.4 The variation of the equilibrium point when τ1=0 and τ2>0.

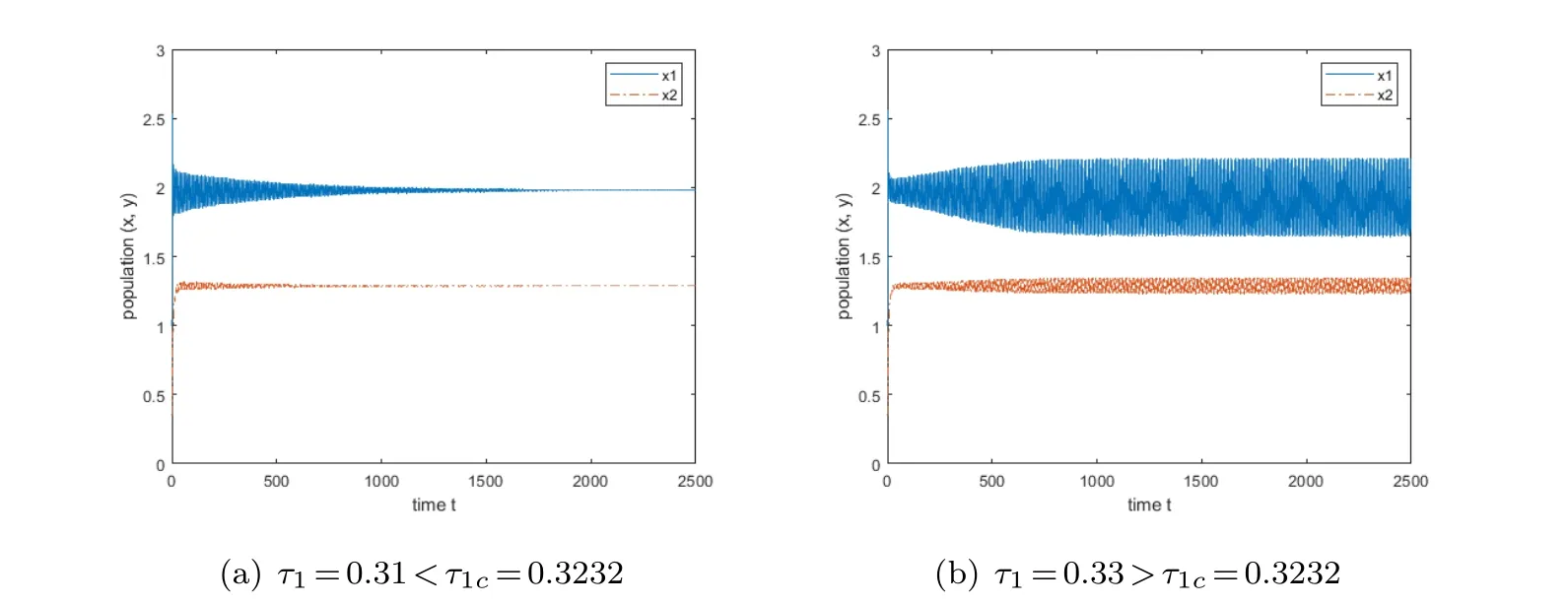
Fig.5 The variation of the equilibrium point when τ1 is the branching parameter and τ2=2.3.

Fig.6 The variation of the equilibrium point when τ2 is the branching parameter and τ1=2.

§6.Conclusion

Models of populations with constant carrying capacity have been studied in much of the literature,neglecting the fact that carrying capacity can be influenced by the activity of biological populations.Thus, in this paper, we construct a more realistic harvest model with a double delay in carrying capacity and prey maturation.The effect of several different combinations of delays on the dynamics of the system is explored.In our model, it is observed that when neither delay exists, the continuous coexistence of the population is not affected, then in the presence of delays, the equilibrium is in a stable state when the time delay is below the critical value, and the coexistence equilibrium is in an unstable state when the delay exceeds the critical value,at which time the Hopf bifurcation occurs.The conclusion indicates that the delay affects the dynamical behavior of the system, which further complicates its dynamical properties.