中深部矿产资源勘探井中阵列激电方法研究

柳建新,黄朝宇,3,汪强强,佟利群,刘海飞,刘 昕,赵莹杰

(1.中南大学 有色资源与地质灾害探查湖南省重点实验室,长沙 410083; 2.中南大学 地球科学与信息物理学院,长沙 410083;3.湖南省国土空间调查监测所,长沙 410129;4.陕西铁道工程勘察有限公司,西安 710000;5.内蒙古自治区呼伦贝尔市应急管理局,呼伦贝尔 021000)

0 引言

目前我国矿产资源的保有储量严重不足,许多老矿山因资源枯竭而面临倒闭,迫切需要在第二找矿空间 (500 m～2 000 m) 开展深部找矿理论与方法的研究,以解决矿山接替资源问题[1-2]。我国大中型危机矿山深边部具有很大的找矿潜力,充分利用矿山原有的成矿模式及丰富的开采资料,深入研究探测深度大、分辨率高的地球物理新方法与新技术,是目前开展深部找矿的一种有效途径。

井中物探方法作为地球物理勘探方法的一个重要分支,主要用来解决井周地质问题,诸如寻找井旁、井底盲矿体,确定其空间位置、形态、产状,追踪和圈定矿体范围,研究钻孔间矿体的连续性等,其突出优点就是能够把场源或测量装置借助钻孔放入地下深处,使其接近探测对象,因此发现井旁隐伏矿体的能力往往比地面物探方法要强[3]。目前在危机矿山深边部找矿中,主要使用的井中物探方法有井中激电法、井中瞬变电磁法、井中磁测及井中重力等[4],其中井中激电法因其观测参数多、观测装置灵活以及对矿质资源反应灵敏等特点,在中深部矿产资源勘探中具有明显的优势[5]。

井中激电法的探测效果是与其正反演解释水平密切相关的。近年来,井中激电法的正反演解释方法得到了快速的发展。J.P.Busby等[6]模拟并分析了井中三极观测装置的多个极化体的电阻率和极化率响应;Klaus Spitzer等[7]采用跨孔偶极和单孔偶极直流激电观测方法,对魁北克西北部Casa Berardi金矿进行了井中激电探测,并采用三维电阻率和极化率正演模拟解释来描述断层构造;Kulessa Bernd等[8]利用钻孔电阻率数据的三维反演对冰川下排水条件进行时移成像;吕玉增等[9]对三维地-井、井-地IP的正反演做了系统研究,编制了地-井、井-地IP三维快速正反演计算程序,开发了地-井五方位IP人机交互正演拟合反演解释软件;F.J.Morrow等[10]基于直流电阻率穿越和跨孔电阻率层析成像法,研究了潮汐对浅层无限制含水层盐分界面的影响;李长伟等[11]实现了三维井中激发极化法正反演,并对快速迭代求解技术进行了研究;熊彬等[12]基于有限差分和异常电位算法实现了时间域井中激发极化法的三维数值模拟,采用一维非零元素行压缩存储模式对所形成的大型稀疏矩阵进行存储,节约了计算所需内存空间,同时引入不完全Cholesky分解稳定化双共轭梯度(ICBU)法求解有限差分线性方程组,提高了求解的效率;白泽等[13]采用了有限差分法和不完全Cholesky共轭梯度法(ICCG)对井地电成像的点源和线源在产生的地表电势异常进行了三维正演模拟,并对地层电阻率数据进行阻尼最小二乘法反演;H.D.Wondimu等[14]在加拿大安大略省北部一个岩浆硫化物矿床的一组19个钻孔中进行了梯度和充电法调查,并对数据反演得到三维电阻率和极化率模型,圈定了矿化带的轮廓;赵荣春等[15]采用基于柱坐标下的放射状网格剖分方式,通过异常电位法对井中激电观测进行了有限元数值模拟,对井中激电观测井旁异常体所引起的激电异常特征进行了研究。这些研究成果推动了井中激电法理论与方法的发展,也为笔者开展井中正反演方法的研究奠定了基础。

采用井中激电法解决危机矿山的中深部找矿问题,首先需要获取足够多的反映深部矿体的信息,而这种深部信息的获取必须充分利用矿体及其外围的发射和接收空间。笔者针对单孔井中激电法进行了初步研究,首先设计了两种多电极系观测方法,以尽可能多地获取井旁地电信息。其次系统研究了井中激电法的二维有限元正演模拟方法以及多种观测方式的联合反演方法,主要包括点源场边值和变分问题、有限元解法、构建反演区域、联合反演方程的建立及约束方式等。最后为验证方法的有效性,编制了Windows界面下的反演软件,对地电模型进行反演试算,反演效果较好,验证了该方法的可行性。

1 单孔井中激电阵列观测方法

在矿区存在钻孔的情况下,可以充分利用地面和钻孔的观测空间,获取大量井旁地电信息,以提高井旁目标体的探测效果。考虑到探测分辨率和野外观测效率问题,笔者在地表三极观测装置的基础上,设计了两种针对单个钻孔情况下的井中激电阵列观测方法。

为提高探测的纵向分辨率,设计的井中激电阵列观测方法如图1(a)所示。观测原理为:将供电电极B(负极)作为无穷远极,放置于离井口较远的位置,其余供电电极A1、A2、…、An(均为正极,相邻电极以等算数间隔或等对数间隔方式排列,可根据勘探要求进行设计)及测量电极M1和M2置于井中,在井中由下至上进行供电和测量。即A1供电M1M2测量,A2供电M1M2测量,…,An供电M1M2测量,第一个测深点测量结束;供电电极A1、A2、…、An及测量电极M1和M2整体向上移动一个点位,重复A1供电M1M2测量,A2供电M1M2测量,…,An供电M1M2测量,第二个测深点测量结束;再继续上移一个点位,再继续供电和测量,如此往复,直到整口井测量结束(或者仅测量某异常深度段),这样可获取井旁不同深度范围内的电性信息。

为提高探测的横向分辨率,设计的井中激电阵列观测方法如图1(b)所示。观测原理为:将供电电极B(负极)作为无穷远极,放置于离井口较远的位置,其余供电电极A1、A2、…、An(均为正极)布设于过井口且垂直异常走向的同一测线上,而测量电极M1、M2、…、Mn由下至上置于井中,地面电极供电井中电极进行差分测量。即A1供电M1M2、M2M3、…、Mn-1Mn同时测量;A2供电M1M2、M2M3、…、Mn-1Mn同时测量;直到An供电M1M2、M2M3…、Mn-1Mn同时测量,至此观测结束。这种观测方式有利于分辨异常体位于钻孔的哪一侧,实际应用中尽量使供电电极排列大于异常体的横向分布范围。

2 井中激电2.5维有限元正演模拟

2.1 波数域点源场的边值问题和变分问题

当点源A置于地下时,波数域电位V的边值问题为[16]

(1)

其中:Ω为积分区域;Γs为地表边界;Γ∞为截断边界;σ为介质的电导率;f=Iδ(x-xA)δ(z-zA)/2为点源项。当点源距离截断边界较远时,第三类边界条件D为

式中:rp和rq分别为点源p及其相对地表的镜像点q至边界积分点的距离;cos(rp,n)和cos(rq,n)分别为矢径rp和rq与积分区域Ω的外法向量n的夹角余弦;λ为波数;K0和K1分别为第二类零阶和一阶修正贝塞尔函数。

利用泛函分析,将方程(1)转化为等价的变分问题

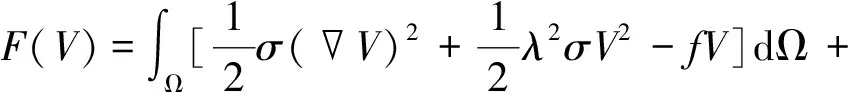
δF(V)=0

(2)

2.2 有限单元法

采用有限元法求解变分方程(2),求解过程如下:

1)单元剖分。考虑到地形因素,将整个研究区域剖分成有限个三角形,具体如图2所示。方程(2)对区域Ω 的积分将转化为对各三角形单元e和边界单元Γe的积分之和:

(3)

图2 地电模型的网格剖分示意图

2)线性插值。若三角形顶点的局部编号记为1、2、3,其空间坐标记为(x1,z1)、(x2,z2)、(x2,z2),电位值记为V1、V2、V3,电导率值记为σ1、σ2、σ3。在三角形单元内,任意一点的电位和电导率均采用线性插值,即:

(4)

其中:V=(V1,V2,V3)T,σ=(σ1,σ2,σ3)T,N=(N1,N2,N3)T,Ni=(aix+biz+ci)/2Δ,(i=1,2,3)为形函数,且a1=z2-z3,a2=z3-z1,a3=z1-z2,b1=x3-x2,b2=x1-x3,b3=x2-x1,c1=x2z3-x3z2,c2=x3z1-x1z3,c3=x1z2-x2z1,Δ=(a1b2-a2b1)/2为三角形单元的面积。

3)单元积分。对剖分区域任意一个三角形单元进行积分,有

(5)

其中:K1e为三角形单元积分的刚度矩阵,K1e=[k1eij]=[k1eij],i、j=1、2、3,并且有

i≥j

式中:α=(σ1+σ2+σ3)/12Δ,β=λ2Δ/60。K2e为无穷远边界线单元积分的刚度矩阵,K2e=[k2eij]=[K2eji],i、j=1、2、3,假如边界单元落在三角形12边上,即i、j=3时,k2eij=0,则边界积分的下三角阵的非零元素为

i≥j

式中:γ=D·l12/12,l12为节点1和2之间的距离。对于场源项Se=[si],i=1,2,3,如果点源与三角形某个节点i重合,则si=0.5,否则si=0。

4)总体合成。对所有三角单元积分结果求和,即得到泛函F(V)的数值表达式

(6)

其中:K是由全部三角单元和边界单元的(K1e+K2e)相加组成的M×M阶对称系数矩阵,各项元素与模型电阻率分布和网格剖分在关;V是由所有M个三角网格节点上的波数域电位组成的列矢量;S则是由Se相加组成的与场源有关的列矢量。对方程(6)中泛函F(V)求变分,并令其为零,进而可得线性方程组

KV=S

(7)

利用一维变带宽压缩存储的乔里斯基分解法求解方程(7),即可得到所有网格节点的波数域电位V,再通过傅氏逆变换

(8)

便可将波数域电位V转换成主剖面y=0上的空间域电位U(x,0,z)。

2.3 计算视电阻率和视极化率

利用式(8)的近似傅氏逆变换公式

(9)

可将前面得到的波数域网格节点电位V转换成空间域电位U。

根据计算公式

(10)

可计算出三极装置的视电阻率ρc。其中UM和UN为测点M和N处的电位;Kc为装置系数,在全空间下Kc=4π/(1/rAM-1/rA*N+1/rA*M-1/rA*N),rA*M和rA*N分别为供电电极A到测量电极M和N的距离,rA*M和rA*N分别为供电电极A关于地表的镜像点源A*到测量电极M和N的距离。

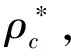
(11)

3 井中激电约束反演

3.1 电阻率联合约束反演

电阻率的线性反演方程通常可表示为[17]:

AΔm=Δd

(12)

其中:A为偏导数矩阵;Δm为模型参数的改正向量;Δd为数据残差矢量。

实际中方程(12)通常是欠定且病态的。为提高反演过程的稳定性和减少反演的多解性,必须在模型空间引入某种约束[18],这里对模型同时施加总体光滑约束Φms和属性约束Φmz,可表示为

(13)

其中:m为反演模型参数向量;mz为已知属性模型参数向量(若网格节点的模型参数已知,则在相应的节点上给定近似真值,否则用背景模型参数代替),C为光滑度矩阵,可采用模型网格节点间的距离构建[19-20],D为对角矩阵(对于模型参数已知的网格节点,则在相应的对角线上给定较大的值(如100),否则设置为1,若仅施加背景约束,则D为单位矩阵)。

当在同一断面采用 种观测装置进行数据采集时,结合式(12)和式(13),在最小二乘意义下构造目标函数Φ为

(14)

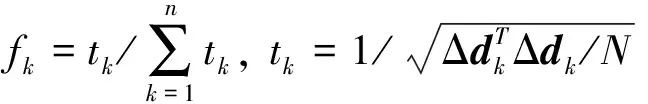
(15)

采用共轭梯度法解方程(15)[21],得到模型参的修正量Δm,将其代入式(16),

m(k)=m(k-1)+Δm

(16)

便得到新的预测模型参数向量m(k)。经过多次迭代,直至实测数据和模拟数据之间的平均均方误差

(17)

满足要求或迭代次数满足终止条件为止,电阻率反演过程结束。

3.2 极化率联合约束反演

在完成电阻率反演的基础上,再进行极化率反演。当地下介质存在激发极化且相对电阻率很小时,视极化率ηa和极化率η之间可近似为线性关系[22]

ηa=Aη

(18)

其中:A为偏导数矩阵(aij=∂lnρci/∂lnρj),在电阻率反演中已经得到。当在同一断面采用n种观测装置进行数据采集时,在最小二乘意义下构造极化率反演的目标函数Φ,并在目标函数中引入光滑和已知属性约束,有

(19)

其中极化率反演的数据加权系数fk根据最后一次电阻率反演迭代的数据拟合误差给定,ηz为井旁已知极化率参数向量,其余参量含义与上述相同。

将式(19)两端对η求导并令其等于零,即可得到极化率的线性反演方程

(20)

采用共轭梯度法求解方程(20),便得到地下介质的极化率。

4 反演算例分析

4.1 模型算例

假定在地下隐伏岩体中赋存三条低阻高极化脉状矿体,岩层及矿脉均倾向于小点号方向。地表剖面长为800 m,井深为800 m,地表布设42根电极,井中布设160根电极。电阻率和极化率模型如图3(a)～图3(b)所示。基于该地电模型对上述观测装置的激电数据分别进行二维有限元数值模拟,井中观测方式的视电阻率和视极化率的模拟结果分别如图3(c)～图3(d)所示,从图3中可看出,在矿脉位置异常呈低阻高极化特征,但位置偏下及难于推断矿脉位于井的哪一侧。地井观测方式的视电阻率和视极化率的模拟结果分别如图3(e)～图3(f)所示,相对井中观测方式而言,这种方式则更好地反映了断面的电性的分布特征,易于推断异常大致形态和埋深,但仍存在向下偏移的现象。

图3 模型反演算例

为提高两种观测方式的探测效果,采用文中联合反演方法将两种观测方式的激电数据联合起来进行反演,当对井旁地质结构信息不了解时,则在反演中只施加光滑和背景先验约束信息,电阻率和极化率的反演结果分别如图3(g)～图3(h)所示,地层倾向及异常形态和埋深得到了较好地反映,但也不同程度地出现了冗余信息。当对地层结构及电性信息有所了解时,可将其作为约束引入到反演中,反演时对上覆三层电性层给定准确的电阻率和极化率值,式(15)中约束矩阵对应的对角线元素设置约束值为100,而下覆两层电性层给定均匀电性值2 500,约束值为1,电阻率和极化率的反演结果分别如图3(i)～图3(j)所示,与仅施加先验约束信息的反演结果相比,地层结构、电性及异常形态均得到了明显的改善。在反演中,可根据对地层结构和电性信息的了解程度,通过人机交互改变约束值和阻尼的大小,改善反演效果。

4.2 水槽模拟实验数据反演

为进一步检验文中井中激电法的探测效果,在长500 cm×宽500 cm×深200 cm的水槽中,开展了井中激电法物理模拟实验,水槽实验照片如图4(a)所示。在水槽中注满清水并添加5 kg食盐,选取多层铝板作为低阻高极化模型,电极布置与铝板的相对位置如图4(b)所示,按文中第2节描述的地表供电井中接收的阵列观测方法采集数据。图4(c)和图4(d)分别为采集的视电阻率和视极化率拟断面图,从图4中可以看出,在接近铝板的接收电极处出现低阻高极化异常带,但对铝板的倾向的反映不明显。采用井中约束反演算法对水槽模拟实验数据进行反演计算,得到电阻率与极化率的二维断面分别如图4(c)和图4(d),从中可以看出,在X方向0 cm～30 cm,埋深20 cm～60 cm范围内呈低电阻率和高极化率特征,异常形态与实际模型吻合度较高,验证了文中井地激电法探测井旁异常体的有效性。

5 结论

笔者针对井旁隐伏矿体勘查问题,对单孔井地阵列激电探测方法进行了研究,得到如下结论:

1)设计了井中和地-井多电极系阵列观测方法,该方法具有观测效率高、获取的信息量丰富、纵向和横向分辨率高等优点。

2)研究了井中激电法的二维有限元正演模拟方法以及多种观测方式的联合反演方法,并对两种电阻率数据进行联合反演解释,反演效果良好,地层倾向、异常形态以及目标体埋深均得到较好地反映,可以尝试将观测方法和反演解释方法在野外生产实践中应用。

3)本项研究可进一步拓展到单孔井中、地井多电极系三维阵列观测及反演解释中。