基于点估计法的配电网最优运行研究
2023-12-29耿亚男潘子妍
耿亚男 潘子妍
(国网北京平谷供电公司)
0 引言
可再生能源 (RER) 在配电系统中的渗透率不断提高, 这意味着系统运营商需要管理风能和太阳能等可再生资源的可变和不确定性, 以持续保持发电和消费平衡。这就需要进行业务变革, 并采购更多的各种辅助服务。传统上, 这些电力系统服务中的许多完全由发电机提供。然而, 在过去的十年里, 需求响应等替代资源越来越有能力提供更多数量的此类电网服务。
1 点估计法分析
点估计法是一种常用的统计推断方法, 该方法基于已知数据来估计未知参数的值。配电网最优运行分析是指通过对配电网拓扑、 负荷、 发电机组等信息的分析, 寻找出最优的操作策略以优化配电网的运行效果。将点估计法应用于配电网最优运行分析, 可以得出参数的估计值, 从而指导决策者做出优化决策。
具体步骤如下:
1) 收集数据: 收集配电网的拓扑结构、 负荷数据、 发电机组信息等。
2) 建立模型: 根据收集到的数据, 建立配电网的模型, 包括节点电压、 线路负载、 功率因数等参数。
3) 参数估计: 利用点估计法估计配电网模型中的参数值。常用的点估计方法包括最小二乘法、 最大似然估计等。
4) 分析优化: 基于参数估计结果, 分析配电网的运行情况, 包括电压稳定性、 负载均衡、 线路损耗等。针对问题, 提出最优化的操作策略, 如调整负荷分配、 装置优化配置等。
5) 结果验证: 将优化策略应用于实际运行中, 观察其效果并进行验证。如果效果不理想, 可以返回第一步, 重新收集数据, 并重新进行估计和分析。
通过以上步骤, 可以利用点估计法对配电网进行最优运行分析, 从而优化配电网的运行效果, 提高供电质量和效率。
2 算法分析
2.1 点估计法
目前, RER 装置在配电网中的高渗透性影响了配电系统的运行。在风力涡轮机(WT) 和光伏发电(PⅤ) 中, 风速和太阳辐射分别是主要能源。由于风速和太阳辐照度的随机行为, 上述能源的发电量存在显著的不确定性。点估计方法将问题输入随机变量的前几个中心矩提供的统计信息集中在每个变量的K点上, 称为集中度。通过使用这些点和关联输入和输出变量的函数F, 可以获得与问题输出随机变量相关的不确定性的信息。
随机变量pl的第k个浓度可以定义为由位置pl,k和权重wl,k组成的一对, 其中位置pl,k是变量pl的第k个值, 函数F 在该值处求值。权重wl,k是一个加权因子, 它解释了该评估在输出随机变量中的相对重要性。通过使用点估计方法, 函数F只需要在K个点上对每个输入随机变量pl进行K次评估, 这些点由第K个位置pl, 输入随机变量pl的K和它们的平均值(μ),m-1 个点上剩余的1 个输入变量组成。因此, 对于m个输入变量, 代价函数的求值为m×k+ 1 次。得到每次求值的输入向量和pl,k如下
式中, ξ 为标准位置,μ和θ为输入随机变量的均值和标准差, 2m+ 1个方法和随机变量权值的标准位置计算如下
式中,λl,3和λl,4为偏度和峰度。本文提出PEM 的概念, 用于处理决策框架中的不确定性。pl的概率实现为
在这些方程中, 最后通过使用加权因子, 从之前研究中获得作为最终结果的输出的期望值:
2.2 需求响应
在本节中, 提出了一个考虑消费者参与DRP 的SDS 运营模型。该模型基于最优潮流, 并在短期内最大限度地降低了分布式网络运营商 (DNO) 的日常能源成本。在所提出的目标函数模型中, 假设DNO 是DER 单元的所有者。因此, DER 装置的操作由DNO完成。了解如何根据DRP 节点对SDS 优化操作的影响来确定DRP 节点的顺序是很有趣的。识别用于参与DRP的节点的优点的技术是将允许参与DR 的节点的总数从1 枚举到负载点的数量。然后, 对于给定数量的允许节点, 使用二进制变量ϕi找到DR参与节点。在每种情况下, 都会识别出最佳节点。每个方案中的选择频率指定了每个节点的优点。
通过DRP, DNO 将其消费者负荷从昂贵时期转移到廉价时期, 以降低成本。需要注意的是, 在本文中, 消费者仅参与使用时间 (TOU) 计划。由于价格差异, 不参与DRP的负荷虚线部分和另一部分能够从一个周期转移到另一个周期, 价格差异可以通过数学方式定义:
2.3 求解算法
蚁群优化 (ACO) 是一种求解组合优化难题的启发式方法, 并已成功地用于解决旅行推销员问题。ACO 算法是基于作为社会昆虫家族成员的真实蚂蚁的行为。根据取决于信息素沉积量的概率转移规则和启发式引导函数, 每个蚂蚁吸引到最短路径。因此,蚂蚁h从城市i到城市j的概率转移规则可以表示如下:
式中,τij为蚂蚁h在城市i和j之间沉积的信息素轨迹,vij为能见度或视线, 等于城市i和j之间的距离或过渡成本的倒数。α和β分别是影响信息素轨迹和启发式引导函数相对权重的两个参数,q为城市i之后将被访问的城市。局部和全局信息素更新由每只蚂蚁根据每只蚂蚁的路线确定, 如下所示
式中,τij(t+ 1) 为一次巡回或迭代后的信息素,ψ为信息素蒸发常数,ε为精选路径权重常数,τo为每只蚂蚁的信息素增量值, Δτij为精选路径的信息素量。
3 仿真分析
本文使用PG&E 69 总线配电系统来解决最优运行问题, 该系统具有两种类型的DG 单元, 包括WT、PⅤ和ESS (储能系统) 。本文的目的是求解在存在RER 和ESS 单元的情况下, SDS 在给定24h 内的随机最优运行。此外, 在所提出的方法中, 还研究了DRP对SDS 优化操作的影响。由于一些可再生能源的间歇性行为和负荷变化, 本文是基于输入数据的不确定性, 采用PEM 方法进行的。在本文中, SDS 被建模为一个具有SDN 和主电网之间电力交换能力的小型迪斯科舞厅。为了考虑智能电网中发电成本的影响, 假设风力发电、 光伏发电和ESS的尺寸和技术等DER的特性不同。
基于以上讨论, 每个DER的每千瓦发电成本是不同的。事实上, 本文被建模为SDS 市场运作中考虑DRP 的运作问题。同时, 在MⅠNLP 的基础上提出了随机操作问题, 并将ACO 算法作为启发式优化算法加以求解。
关于PEM 的随机分析在运营、 规划、 机组承诺问题研究等方面具有良好的前景。事实上, 在这种情况下, 可以评估负荷、 风电和太阳能短期调度中的预测误差。
SDS 的电压分布如图1 所示。根据该图, 通过在SDS的操作中使用所提出的DRP方法, 电压分布比没有DRP 的情况下得到了更多的改善。根据这个数字,随着与传统网络中变电站的距离, 它们将面临电压下降。SDS中DER的正确操作可以改善电压分布。
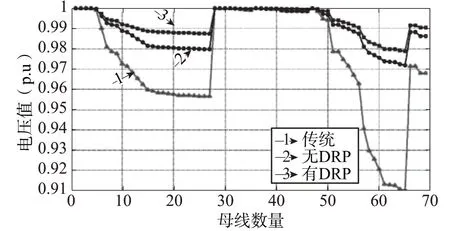
图1 有无DRP的配电系统的电压分布
对于不同的DRP, 结果载荷分布如图2 所示, 结果表明, 需求转移使总负荷分布趋于平缓。可以看出, 负荷从高价格时期 (高峰) 转移到其他时期 (非高峰), 以最大限度地降低运营成本。在本文中, 假设所有负荷点都被认为是灵活应用DRP的, 电力采购来源被认为是双边合同。根据获得的结果, 表明在运行DRP时, 由于DNO策略, 需求和负载形状可能会发生变化。此外, 本文表明, 当考虑大量输入随机变量(包括连续和离散) 时, 2m+1 方案的使用提供最佳性能。
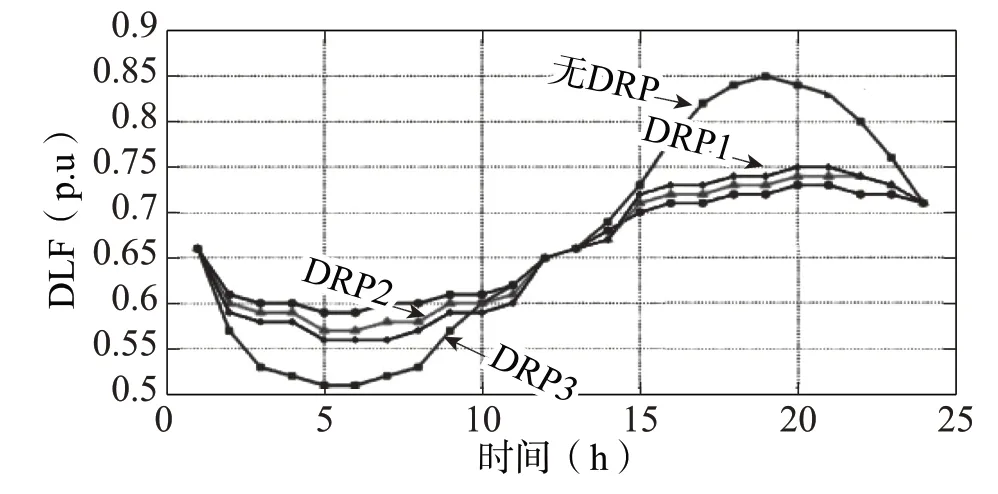
图2 有无DRP的负载点配置文件
4 结束语
本文提出了一个考虑DRP 的SDS 随机最优操作框架, 该框架考虑了DER的经济性和可靠性操作。采用PEM 方法对可再生电力和负载等SDS 组件的不确定性进行建模。SDS 的经济可靠运行被表述为MⅠNLP 优化问题。基于SDS 与主网之间电力交易的经济分析, 对DER 和负荷进行随机建模, 以确定SDS在最小成本下的最优运行。基于DER 单元的每个发电功率的结果, 在考虑优化约束的情况下确定。应用ACO 算法来最小化成本函数作为优化算法。研究表明, 通过参与DRP, 由于负荷从高价时段转移到其他时段, 降低了电力损失成本、 DER 运营成本和ENS 成本等运营成本, 并使每个时段的负荷分布趋于平缓,降低了最大需求。从研究结果还可以得出, 网络的电压分布和功率损耗强烈依赖于DRP。研究表明, 适当的操作条件对DNO 成本有很大影响。此外, 结果表明, 调节SDS 与主电网之间的电力需求和交易是可能的。
