基于改进滑动窗口的渔船轨迹在线压缩算法

顾杰, 宋鑫, 施笑畏, 苌道方

(1.上海海事大学物流工程学院,上海 201306;2.上海海事大学青岛研究院,山东 青岛 266237;3.上海海事大学物流科学与工程研究院,上海 201306)

0 引 言

船舶自动识别系统(automatic identification system, AIS)由岸基(岸台基站)设施和船载设备共同组成,它能够将船舶识别码、船位、对地航向、船首向、航速、船舶尺度、船型和货物等相关信息通过甚高频(very high frequency, VHF)向附近水域船舶和岸台广播,使邻近船舶和岸台能及时掌握附近海面所有船舶的动态和静态信息。随着国家对渔业重视程度的不断增加,AIS已经在渔业信息化建设中得到广泛应用[1]。海事部门和渔业管理部门可以利用AIS提供的渔船航行、渔业生产信息等对渔船进行管理。[2]渔船作业区域相对集中,且海区内渔船密集程度较高,因此监管人员若要通过AIS掌握渔船的实时状态,就需要渔船能够及时、准确地上传AIS数据。然而,海量的轨迹数据会长时间、高频率地占用数据传输的通道,导致其他可能需要协调避让的船舶错过沟通的良机,从而影响海上的航行安全。[3]此外,目前渔船上普遍使用的AIS设备为B类AIS设备,其功能存在缺陷且发送信息的速度较慢,致使渔船AIS数据难以被有效利用。因此,需要快速高效的在线AIS轨迹数据压缩算法对数量庞大的AIS数据进行压缩。

船舶轨迹压缩主要分为离线压缩和在线压缩两种,其中最经典的离线压缩算法是DOUGLAS等[4]提出的DP(DOUGLAS-PECUKER)算法。由于DP算法在用于对数据进行离线批处理时具有较好的效果,很多学者在DP算法基础上进行了更深入的研究:徐凯等[5]提出一种考虑时间维的快速DP算法,利用向量的内积、外积改善算法的压缩效率和运行速度;ZHAO等[6]在根据空间位置特征采用DP算法的同时,考虑了航向变化和速度特性;LIU等[7]和TANG等[8]均对自适应阈值的DP算法进行了研究。在在线压缩领域影响较广的是KEOGH等[9]提出的滑动窗口(sliding window,SW)算法:高邈等[10]通过加入风流压差角降低SW算法的误差;GAO等[11]根据船舶航向角偏差、位置偏差和AIS数据的时空特性从船舶轨迹中提取关键特征点,对SW算法进行了改进;董婉婷等[12]以相邻轨迹点间的经纬度变化趋势为参照来保留特征点,在压缩高密度停滞点的同时用采样法保留直行中间点,从而避免采用SW算法压缩轨迹可能出现的轨迹形态失真。宋鑫等[13]提出一种动态阈值结合全局优化的两阶段在线压缩算法,在分段提取特征点后利用改进的SPM(scan-pick-move)算法进行全局优化,在提高压缩效率的同时取得了良好的压缩效果。SUN等[14]将滑动窗口添加到经典的SPM算法中。ZHU等[15]采用滑动窗口中的轨迹变化率和速度变化率作为当前轨迹点是否可以简化的判断标准。

上述在线压缩算法用于对航线较为固定、AIS数据质量较好的商船轨迹的压缩能够取得较好的效果,但在用于处理沿岸航行的渔船的轨迹数据时会丢失大量轨迹特征点。这是由于:海上船舶远洋航运的航线较为固定,在一段时间内采集到的船舶航迹数据具有一定的重复性和规律性;渔船不会沿着固定的航道航行,且其航向和航速变化较大,特别是在进行捕捞作业时渔船会在作业区停留较长时间并在某个区域来回慢速航行,因此在对渔船轨迹数据进行压缩的过程中采用单一的距离阈值难以考虑渔船航向的变化,而采用多种阈值组合不仅会误删一些局部的特征点,而且会大大提高算法的时间复杂度。

为解决传统算法在渔船轨迹点密集处易丢失轨迹,难以保留方向变化较大的特征点的问题,本文提出一种基于改进滑动窗口的渔船轨迹在线压缩算法。该算法结合船舶领域的思想,在原本的滑动窗口中构造一个以窗口起止点为焦点、以距离阈值为短轴半径的椭圆形船舶领域,在考虑时序信息和传统距离阈值的同时,保留一部分局部方向变化较大的特征点,从而实现更有效的轨迹数据在线压缩。

1 算法压缩原理

船舶轨迹压缩的原理是:以较少的点表示原有的轨迹,并且尽可能减小压缩轨迹的误差。如图1所示,轨迹点P1和P2分别为当前窗口的起始点和终止点,其余的点为当前窗口内待处理的轨迹点。简化阈值是指从原始轨迹点到简化轨迹线的最大允许欧氏距离(perpendicular Euclidean distance, PED),而与直线P1P2平行的两条虚线内的区域就是待压缩的区域。压缩时计算每个轨迹点到直线P1P2的欧氏距离,因为d3、d5的长度小于简化阈值而d4的长度大于简化阈值,所以仅有P4被保留下来。然而,仅以欧氏距离作为压缩阈值是难以判断船舶航向角的变化的。以图1中(P1,P5,P2)轨迹段为例:船舶在行驶过程中航向发生了很大的变化,轨迹点P5因其包含较大的信息量而被作为特征点保留,但实际上根据上述压缩算法P5会因其到直线P1P2的欧氏距离小于简化阈值而被删除。

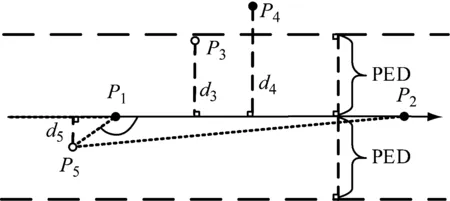
图1 经典的船舶轨迹压缩原理示意图

由于渔船不受固定航道的约束,其运动模式与其他类型船舶的相比较为复杂,所以渔船轨迹相较于其他船舶的轨迹存在数据点密集、航速和航向波动较大的特点。为在压缩轨迹的过程中加入对船舶航向的考虑,保留更多的特征点,在此引入船舶领域的概念。船舶领域本义是指围绕船舶的自由空间,由日本学者藤井弥平于20世纪60年代初提出,目前主要应用在船舶避碰、碰撞风险评估、航道容量分析这几方面[16]。如图2所示,FUJII等[17]提出的椭圆形船舶领域模型,椭圆的中心为船舶中心,椭圆的长轴在船舶首尾连线上,椭圆的短轴在正横方向上,船舶领域的大小与船长L成正比。传统的船舶领域实际上是一个围绕该船的、将其他船舶和固定物体排除在外的有效水域,通过划定一个界限来保证该船附近没有其他船舶或障碍物存在,从而使其自身始终处于较为安全的状态。借鉴船舶领域思想,本文构造了一个以滑动窗口的中心为中心,用于将轨迹点筛除的特殊区域。

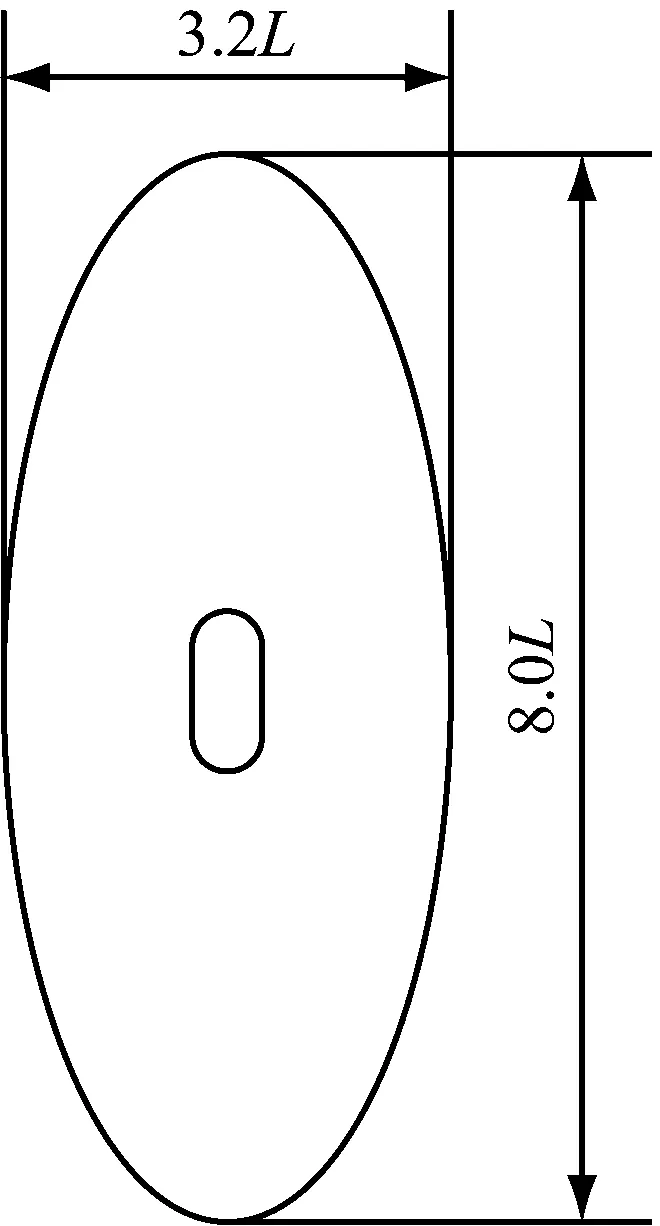
(a)模型1

在轨迹压缩研究领域,POTAMIAS等[18]首次在threshold-guided sampling算法中提出“安全区域”的概念。如图3所示,该算法通过限定最后一个轨迹点速度的可容忍变化以及方向的最大允许偏差来控制安全区域的实际形状,通过判断轨迹点是否落在此安全区域内决定是否保留轨迹点,从而达到轨迹简化的目的。ZHANG等[19]在改进DP算法时针对简化阈值这个唯一参数,提出一种新的基于AIS数据的最小船舶区域评价方法。为保证原始轨迹点对应的简化轨迹点的位置在原始轨迹点的安全范围内,采用船舶领域的大小作为阈值确定的标准。

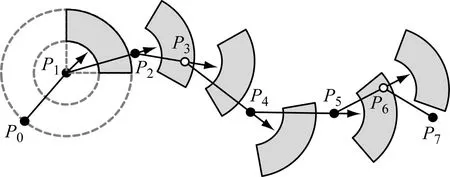
图3 POTAMIAS等[18]在threshold-guided sampling算法中提出的安全区域

本文结合船舶领域的思想,在滑动窗口中划定一个椭圆形的界限作为船舶轨迹压缩的依据,该界限之外的点均被作为特征点保留。以图4为例,以窗口的起始点P1和终止点P2作为焦点构造标准椭圆,将轨迹点到直线P1P2的欧氏距离作为短轴半径,轨迹点如果被包含在船舶领域内则被删除,否则被作为特征点保留,即在图1的基础上保留了更多、更有价值的特征点。从图4可以看出:类似P5这样的方向变化较大且距离窗口起始点有一定距离的轨迹点因位于船舶领域外而得以保留;类似P3这样的方向变化较小且欧氏距离小于阈值的轨迹点被删除。以船舶领域作为筛选特征点的依据,不仅可以保留更多特征点,还可以避免点弦距离的计算。改进后的算法利用椭圆的第一定义,比较轨迹点到窗口起始点与到终止点的距离之和与船舶领域的长轴长度的大小,若前者大于后者则判定轨迹点在船舶领域外,反之判定轨迹点在船舶领域内。与原算法相比,这样的判断方式不仅能够保留更多有用的信息,还能够减少海伦公式的使用,使得算法的时间复杂度降低。

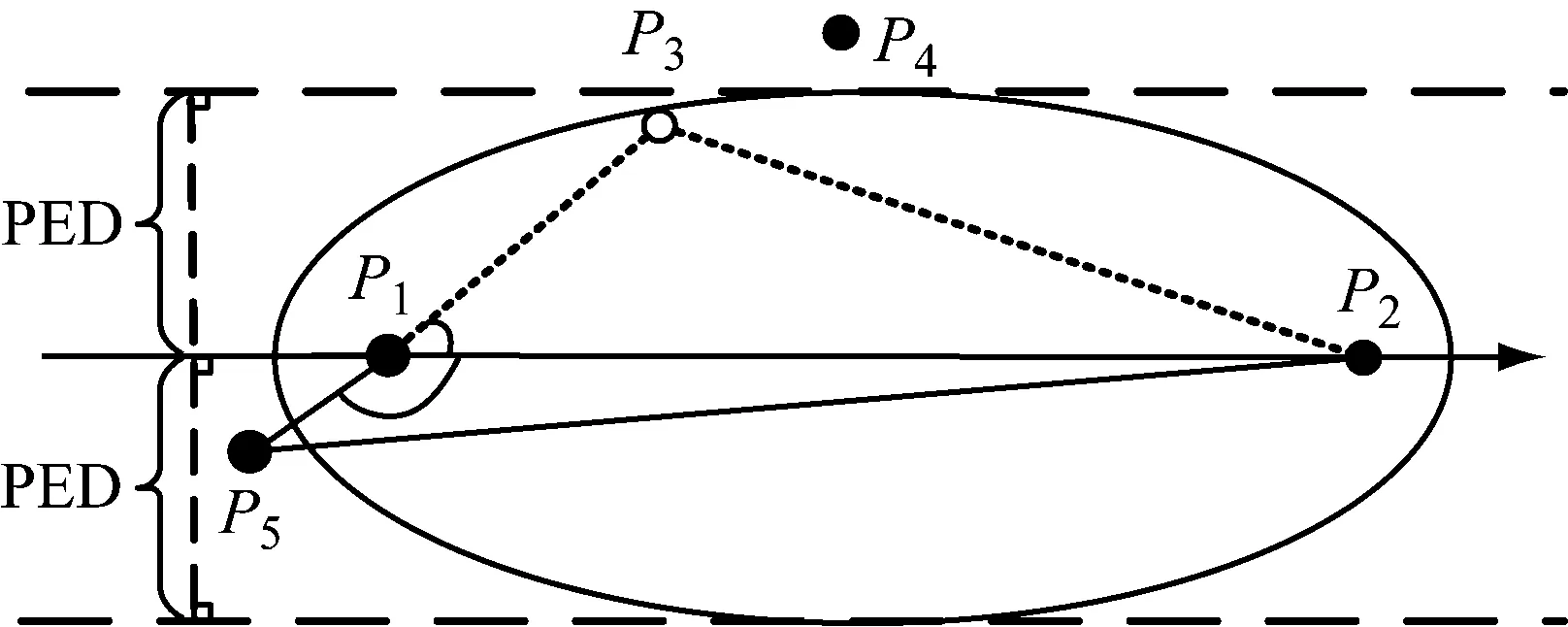
图4 结合船舶领域的轨迹压缩原理

2 算法设计与实现

2.1 相关定义与公式

定义1所有的轨迹点数据均由三元组组成,上传的AIS轨迹数据中轨迹点i的数据为

pi=(xi,yi,ti)

(1)

式中:xi和yi分别为轨迹点i的经度和纬度;ti为船舶经过点i的时间。

定义2原始轨迹T是指渔船在航行过程中上传的AIS轨迹数据集合,该轨迹含有n个轨迹点,可以表示为

T={p1,p2,…,pn},pi∈T

(2)

简化轨迹Tsim是指原始轨迹经过压缩处理后保留的特征点集合,该轨迹含有m个轨迹点,可以表示为

(3)

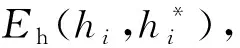
hi=pi·pi+1,pi≠pn

(4)

(5)

(6)

定义4在原始轨迹中的某一轨迹点所在滑动窗口创建一个椭圆形可变船舶领域(用SD表示),用于判断该轨迹点是否应被剔除。该标准椭圆以滑动窗口的起始点与终止点的距离为焦距,以欧氏距离阈值为短轴长。

在预处理数据时,需要将初始数据的WGS-84大地坐标系转换成墨卡托坐标系,假设某轨迹点的经纬度坐标为(φ,ω),平面坐标为(x,y),则转换公式如下:

(7)

(8)

x=r0ω

(9)

y=r0q

(10)

式中:r0为基准纬度圈的半径;e为地球椭球第一偏心率;a为地球椭球长轴半径;q为等量纬度。

2.2 基于改进滑动窗口的渔船轨迹在线压缩算法

2.2.1 经典SW算法

经典SW算法的思想是:在起点初始化一个滑动窗口,保证窗口的大小始终为3个点并逐步加入轨迹点实现在线压缩。判断某轨迹点能否被作为特征点保留的依据是:计算待处理点到窗口起始点与终止点连线的欧氏距离,若该欧氏距离大于设定的阈值,则将该待处理点作为特征点保留并将终止点作为新窗口的起始点继续压缩,若该欧氏距离小于阈值则将窗口的终止点向后滑动,重复上述步骤直到所有的轨迹点都被处理完毕。如图5所示,初始滑动窗口为(P0,P1,P2),点P0作为起始点得以保留。计算待处理点P1与线段P0P2之间的欧氏距离,若该欧氏距离小于阈值,则剔除点P1并加入新的轨迹点P3作为窗口(P0,P2,P3)的终止点。继续计算待处理点P2到线段P0P3的欧氏距离,由于该欧氏距离超过设定的距离阈值,所以点P2作为特征点被保留。加入点P4,点P2成为新的窗口(P2,P3,P4)的起始点,重复上述步骤,得到最终的简化轨迹为(P0,P2,P3,P4,P6,P7)。

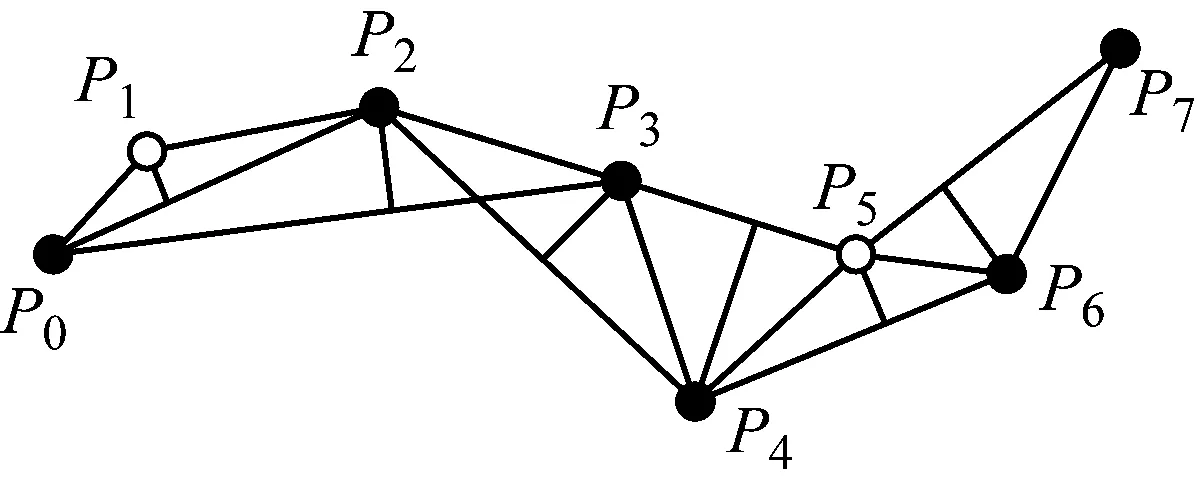
图5 经典SW算法

2.2.2 改进的SW算法

针对渔船AIS数据变化幅度大的特点,结合船舶领域的思想,提出基于改进滑动窗口的渔船轨迹在线压缩算法。由于渔船轨迹数据量大,且在渔船航行过程中航向和航速等变化频繁,经典SW算法以单一的欧氏距离阈值作为筛选标准很难保留所有的特征点,所以经典SW算法对渔船轨迹数据的压缩率不高。本研究对经典SW算法加以改进,选取原窗口内的起始点和终止点作为标准椭圆形船舶领域的焦点,原来的距离阈值作为标准椭圆的短轴半径,在压缩的轨迹带中构造一个筛选能力更强的椭圆形船舶领域。

算法流程见图6。算法基本步骤如下:

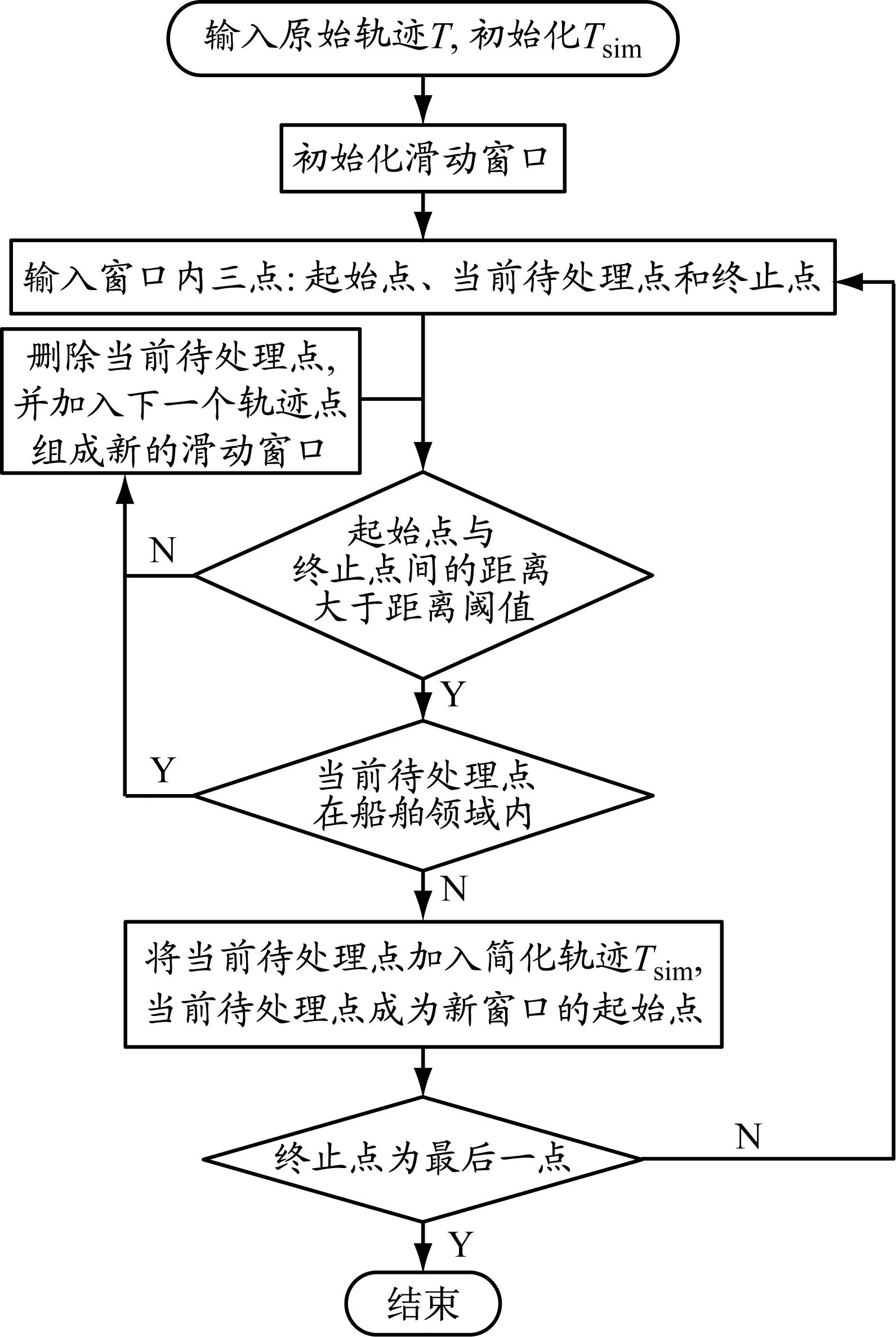
图6 改进SW算法流程

(1)输入原始轨迹T,并将第一个轨迹点加入简化轨迹Tsim,初始化滑动窗口。

(2)为防止渔船在某一位置长时间保持静止,若当前窗口的起始点与终止点之间的距离小于距离阈值,则直接剔除当前待处理点,并加入下一个轨迹点组成新的滑动窗口。

(3)令当前滑动窗口为(P0,P1,P2),即P0和P2分别为滑动窗口的起始点和终止点。若P0与P2之间的距离大于距离阈值,则以P0与P2之间的距离为焦距、以欧氏距离阈值为短轴半径构造椭圆形船舶领域SD。判断点P1是否在船舶领域内,若在领域内则剔除点P1并加入下一个轨迹点,组成新的滑动窗口(P0,P2,P3),否则将点P1作为特征点加入简化轨迹Tsim,并将点P1作为新窗口的起始点(滑动窗口变为(P1,P2,P3))。

(4)继续执行算法,直到滑动窗口的终止点为原始轨迹T的最后一点,算法结束,输出简化轨迹Tsim。

3 实验验证与分析

3.1 实验设计

为验证基于改进滑动窗口的渔船轨迹在线压缩算法的有效性,进行单船轨迹的不同阈值分析以及该算法与其他算法的对比分析。算法采用Python3.9编写,实验设备的具体配置为:Windows 10,Intel(R) Core(TM) i7-10750H 2.6 GHz,16 GB内存。本文的原始数据集来自中国港口网(http://ship.chinaports.com/)。随机选取2021年4月1—30日东海沿岸100艘渔船的轨迹,共450 162条数据。

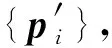
EAED(T,Tsim)=

(11)

(12)

3.2 单船轨迹压缩结果

在数据集中随机抽取一艘MMSI为900406865的渔船在2021年4月的一条AIS轨迹数据,共有1 307个轨迹点。在距离阈值取50 m时,用经典SW算法压缩后剩余的轨迹点数为807,用改进后的SW算法压缩后剩余的轨迹点数为948。单条轨迹的压缩结果见图7,其中:图7(a)为完整轨迹;图7(d)为船舶前进的轨迹段;图7(g)为船舶无规则运动的轨迹段。对比图7(e)与图7(f)可知,改进后的SW算法对船舶航向的变化更加敏感。对比图7(h)与图7(i)可知,在较为复杂的航行情况下,用改进后的SW算法压缩船舶轨迹可以在船舶航向变化较大的局部区域保留更多的有用信息,从而保证压缩后的轨迹不失真。通过对压缩前后渔船轨迹的对比可以看出,虽然用本文算法压缩后仅剩72.5%的轨迹点,但是所得轨迹仍能近似地表现出原轨迹的特征。

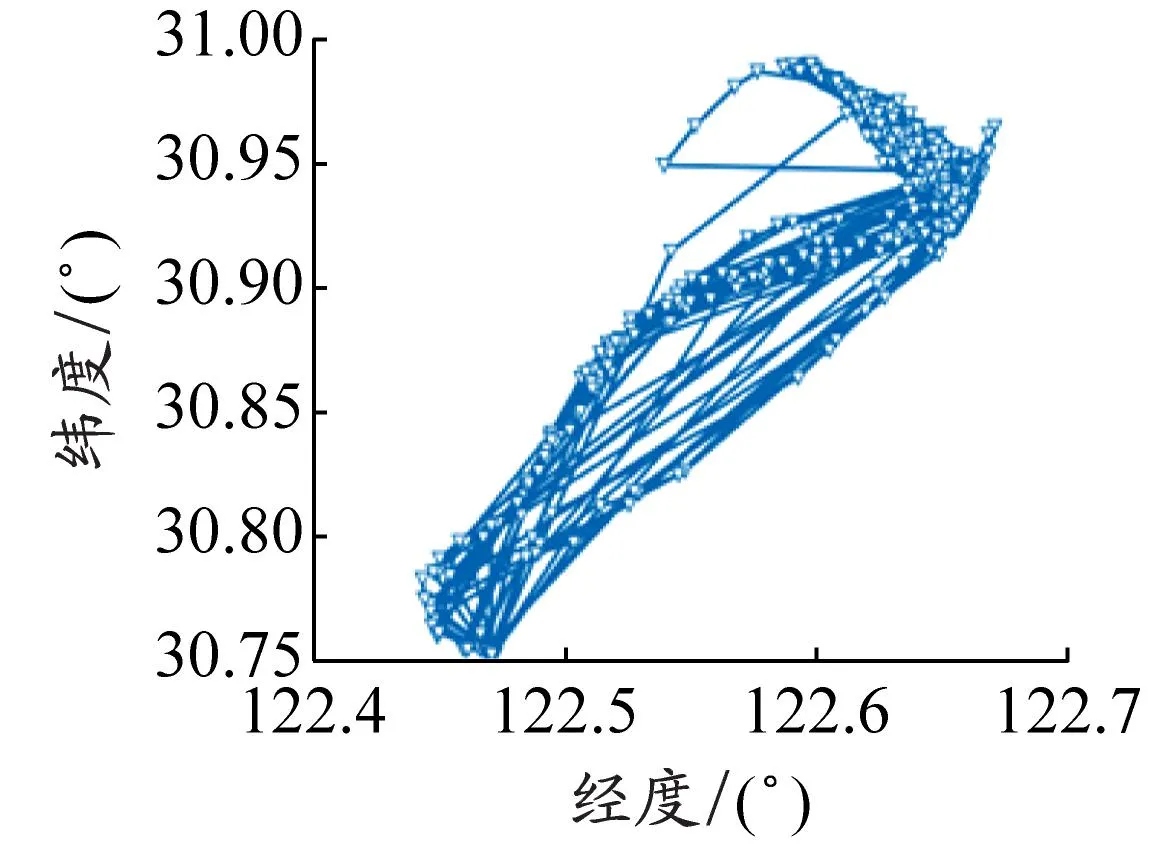
(a)完整轨迹

由于压缩数据的目的是为了后期更方便地进行分析,所以压缩的首要前提是保证压缩后轨迹的误差尽可能低,而不是仅以压缩率作为算法的评价指标。本实验对欧氏距离阈值、压缩率和平均欧氏距离误差这三者之间的关系进行了分析。如图8所示,随着欧氏距离阈值的不断增大,压缩率不断减小,但平均欧氏距离误差加速增大,数据所保留下来的有用信息越来越少,因此盲目增大压缩阈值会使得轨迹关键特征点信息被删除的风险变大。虽然算法选取较高的压缩阈值能够压缩掉大量的轨迹点,但是所得轨迹的失真度会增加,最终影响压缩轨迹数据的质量。因此,在轨迹压缩的过程中,应当根据实际的需求选择合理的阈值,确保能够保留关键特征点,从而使压缩得到的轨迹能够有效代替原始轨迹。

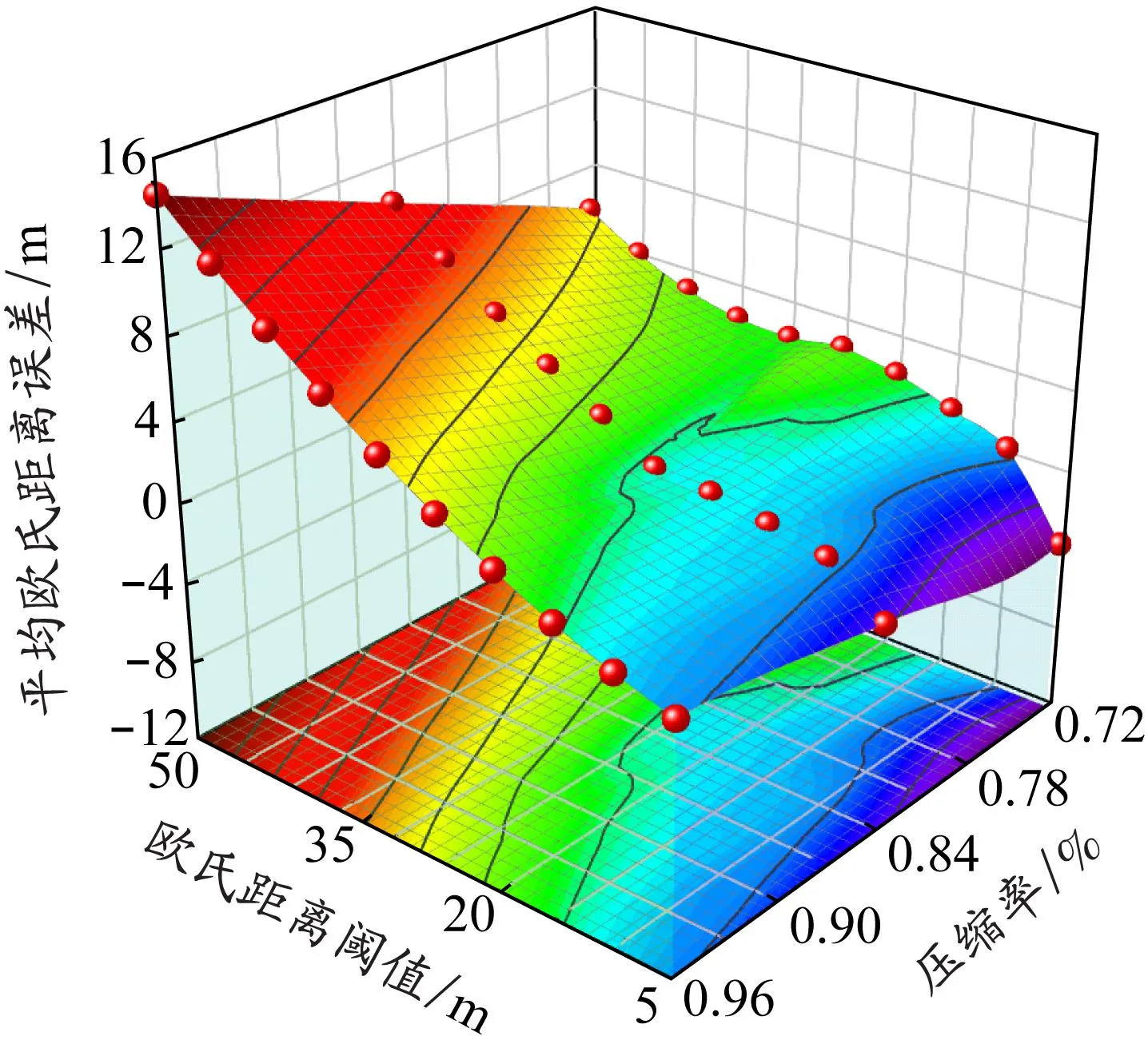
图8 距离阈值、压缩率和平均距离误差的关系

3.3 不同阈值下各算法的比较

为比较各算法在不同阈值下的压缩效果,对于DP算法、TD-TR算法、SW算法和本文改进后的SW算法设定距离阈值分别为10、20、30、40、50 m,对于SQUISH算法设定压缩率阈值分别为95%、90%、85%、80%、75%,对450 162条AIS数据进行压缩。5种算法的轨迹数据压缩结果见表1。由表1可知:(1)随着阈值逐渐增大,各算法的压缩率均呈明显的下降趋势。(2)在平均欧氏距离误差和平均方向误差对比方面,DP算法和TD-TR算法比SW算法和SQUISH算法更具优势。这是由于DP算法和TD-TR算法属于离线批处理算法,能够对渔船轨迹进行全局处理,而SW算法和SQUISH算法作为在线压缩算法,更偏向于从局部提取特征点,难以兼顾轨迹的全局变化情况。(3)本文提出的改进SW算法不仅在平均欧氏距离误差的控制上更出色,而且弥补了经典SW算法忽略船舶航向变化的缺点,对渔船航行过程中的方向变化更为敏感,压缩所得轨迹的平均方向误差在5种算法中是最小的。

不同算法运行时间的对比见图9。由图9可知,随着轨迹点数的增加,5种算法的压缩时间都增加。SQUISH算法压缩时间的增加幅度最大,这是由于优先队列的容量随轨迹点数的增加而增大。由于数据的成倍增加使迭代次数增加,所以DP算法和TD-TR算法压缩时间的增长幅度也较大。本文提出的改进SW算法在压缩速度上不仅继承了经典SW算法的优势,还在原有基础上有小幅度的提升,能够更好地用于在线压缩的场景。

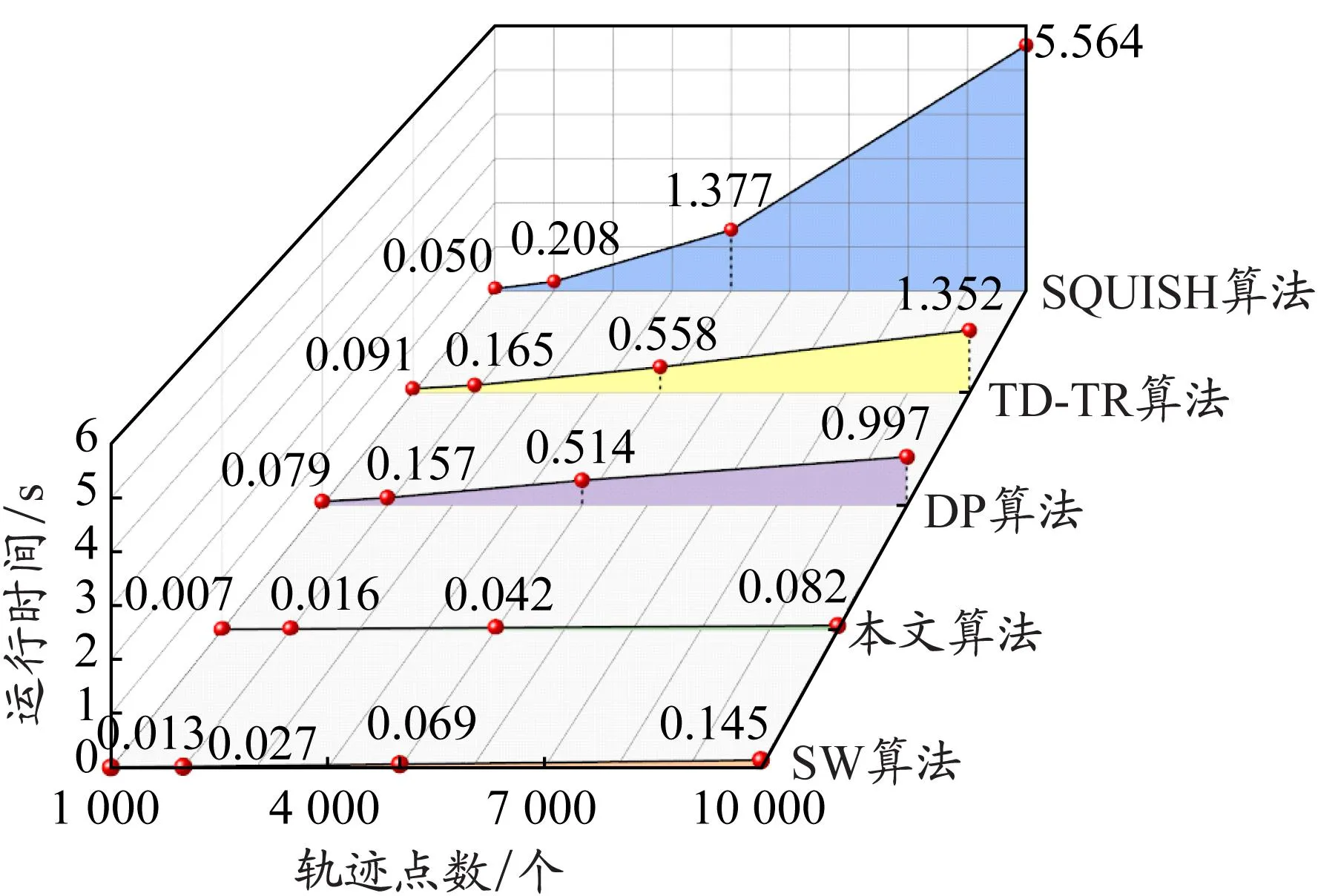
图9 算法运行时间对比

4 结 论

针对现有轨迹压缩算法仅以欧氏距离为压缩阈值,在渔船轨迹点密集处易丢失轨迹,难以保留方向变化较大的特征点等问题,结合船舶领域的思想,提出一种基于改进滑动窗口的渔船轨迹在线压缩算法。采用东海沿岸的渔船AIS数据进行对比实验,结果表明该算法与经典滑动窗口算法相比在不增加算法运行时间的同时,在不同阈值下压缩率平均提高了5%左右,不仅能在压缩时保留更多方向变化较大的轨迹点,而且压缩后得到的轨迹相对于原始轨迹的误差更小,具有一定的理论研究价值。本文的研究也存在一些不足,如在轨迹压缩中未考虑不同水域(开放水域、限制水域、狭水道、冰区等)的不同特点,也未考虑不同渔船的船长、吃水的差异。未来将在轨迹压缩过程中考虑更多的船舶参数以提高压缩后轨迹的精度。