基于改进粒子群算法的海流环境下无人水面艇路径规划

白响恩, 孙广志, 徐笑锋

(上海海事大学商船学院,上海 201306)

0 引 言

随着人工智能技术的不断发展和海上作业需求的日益增长,无人水面艇(unmanned surface vessel,USV)获得了世界范围内的广泛重视。USV由于其灵活性强、成本低、环境适应性强,在海洋采样和环境检测、海岸巡逻和救援、资源勘探等领域发挥着重要作用[1]。然而,USV在执行任务时面临的最大挑战是安全导航[2],即在复杂的海洋环境中为USV规划出一条高质量且无冲突的路径,使船舶安全抵达目的地。为保证USV能够安全地执行任务,USV的路径规划问题变得越来越重要。

目前路径规划按照对环境信息的掌握程度可分为全局路径规划和局部路径规划[3]。全局路径规划就是在给定的空间内根据规划目标和任务要求找到一条从起点到终点的路径。大量的文献将全局路径规划描述为一个单目标优化问题,规划的目标分别为路径长度、能耗、路径平滑度、安全性等。龙洋等[4]以路径长度为适应性函数,采用混合细菌觅食算法搜索USV的最短路径。LEE等[5]提出一种考虑环境影响和航向角的最优路径规划算法,目标是找到一条能耗最少的路径。然而,能耗、路径平滑度和安全性都是USV路径规划的关键目标。USV在航行期间的能耗决定了USV的续航性,影响航运成本;路径平滑度影响USV的机动性;安全性是确保USV顺利执行任务的基本要求。因此,在进行USV路径规划时必须考虑环境因素和多目标优化问题。

粒子群(particle swarm optimization, PSO)算法是一种基于群体智能的进化算法,具有简单、易于实现等优点[6],常被用于求解路径规划问题,但存在两个缺点:随着不断迭代种群多样性会下降,算法容易产生过早收敛的问题;算法容易陷入搜索停滞状态,难以跳出局部最优解。为此,许多学者对PSO算法进行改进:周新宇等[7]提出了一种基于精英反向学习(elite opposition-based learning, EOBL)的PSO算法(记为EOBL-PSO算法),极大地提升了算法的收敛精度;巫光福等[8]为全局最优粒子的速度添加干扰量,并引入非线性惯性权重,有效地提升了算法的收敛速度。除了通过改进PSO算法中的参数提升算法的性能,还有许多学者将PSO算法与其他智能优化算法进行融合:郑佳春等[9]将模拟退火(simulated annealing, SA)算法与PSO算法相结合(记为SA-PSO算法)来求解USV的路径规划问题;曹梦龙等[10]将PSO算法与灰狼算法融合用于机器人路径规划。

基于上述文献分析,本文以路径长度、能耗和路径平滑度为优化目标,构建USV的多目标路径规划模型,提出一种基于EOBL的自适应PSO算法(记为EOBL-APSO算法),在有海流和障碍物影响的环境中进行USV路径规划,并对模型的有效性进行验证。

1 USV在海流环境下的运动模型

为提高算法的计算效率[11],只考虑USV在水平面上的运动状态。参考大量关于海流对USV运动影响的文献,通过叠加多个黏性Lamb涡流,建立时变分布的二维海洋环流模型[12]。仅考虑海流运动的空间变化,故假定海流在USV航行期间在区域内的运动是稳定的。该时变海流速度场的函数表达式如下:

式中:x和y分别为二维空间区域内任意一点的横坐标和纵坐标;xc,0和yc,0分别为涡流中心的横坐标和纵坐标;H为涡流强度;δ为涡流半径;vc,x、vc,y分别为涡流在x和y轴方向上的速度分量。

假设USV处于图1所示的海流环境中,USV的速度为v,航向角为φ,则USV在x和y轴方向上的速度分量vx和vy分别为

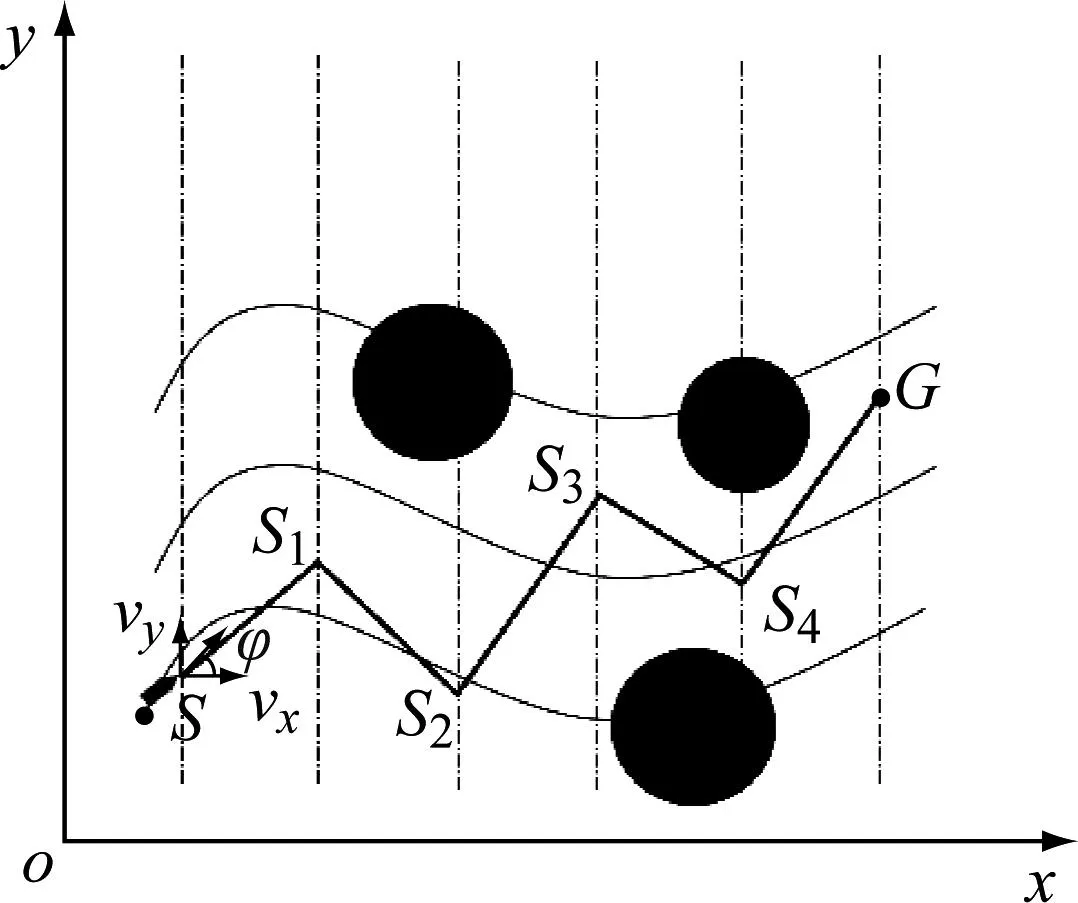
图1 USV所处的海流环境及路径示意图

vx=vcosφ+vc,x

(4)

vy=vsinφ+vc,y

(5)

式(4)和(5)可以反映海流环境下USV的运动状况。为使USV能够正向运动到目的地,USV的速度必须大于零,即vx>0,vy>0。图1中,路径起点为S,路径终点为G,Sk(k=1,2,3,4)为起点S与终点G之间的路径点。

2 USV的路径规划模型

2.1 环境和路径描述

在复杂的海洋环境下寻找一条能避开障碍物并满足约束条件的最优路径是USV路径规划的主要任务。通常复杂的海洋环境主要由风浪流、岛屿、礁石以及人工建设的海洋基础设施等组成。本文主要研究海流对USV的影响,为此模拟了2种海流环境:固定海流环境和时变海流环境。将岛屿、礁石等不规则障碍物抽象为圆,因此环境主要由海流和圆形的障碍物构成。如图1所示:从起点S到终点G的路径点依次为S,S1,…,G;黑色虚线为等间距线。每个路径点都落在等间距线上,这样就可以预先得到每个路径点的横坐标,由此只需求解满足规划目标的路径点的纵坐标。

2.2 多目标优化函数

为避免各优化目标之间的冲突,给每个优化目标赋予相应的标准化因子。USV路径规划的多目标函数为

z=ω1L+ω2E+ω3F+C

(6)

式中:L为路径长度,E为能耗,F为路径平滑度,这3个目标函数值的量纲均为1;ω1、ω2、ω3分别为路径长度、能耗、路径平滑度的标准化因子,通常是根据USV的工作环境和实际经验设定的;C为碰撞指标。z最小时对应的路径为全局最优路径。

2.2.1 路径长度计算

(7)

式中:n为路径点的数目;xk、yk分别为第k个路径点的横坐标和纵坐标。

2.2.2 路径平滑度计算

如图2所示,Sk、Sk-1和Sk+1分别为USV的当前路径点、上一个路径点和下一个路径点,其坐标分别为(xk,yk)、(xk-1,yk-1)和(xk+1,yk+1),则路径段的角度θk的计算式为

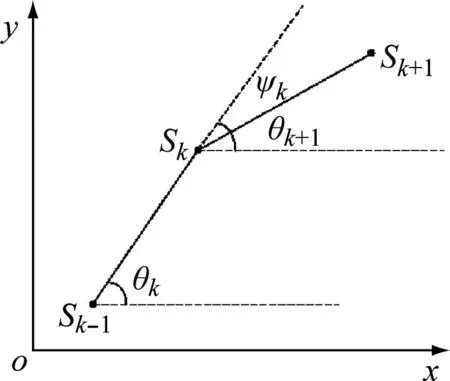
图2 路径段角度

(8)

因此,路径平滑度的计算式为

2.2.3 能耗

USV在航行过程中的能耗受到海流的影响:当USV的航向与海流方向保持一致时,USV能获得来自海流的推进力从而能耗降低;当USV的航向与海流方向相反时,USV需要消耗大量的能量来克服海流的阻力从而能耗增加。本文在研究海流对USV能耗的影响时将重点放在USV的速度变化上。在计算USV的能耗时,先根据USV在海流环境下的速度v′和每段路径的长度lk计算出每段路径的航行时间tk,再参考文献[13]计算每段路径的能耗Ek,最后求和得到整条路径的能耗E。

式中:P为USV发动机的额定功率。

2.2.4 碰撞指标

C是用来检测USV是否与障碍物碰撞的指标,用于确保获得的可行路径与障碍物保持一定的安全距离。针对传统PSO算法规划出的路径存在紧贴障碍物的问题,考虑USV自身大小,在路径规划中规定USV处于半径为R的安全区域内(见图3),在此安全区域内不得含有任何障碍物[14]。C的计算式如下:

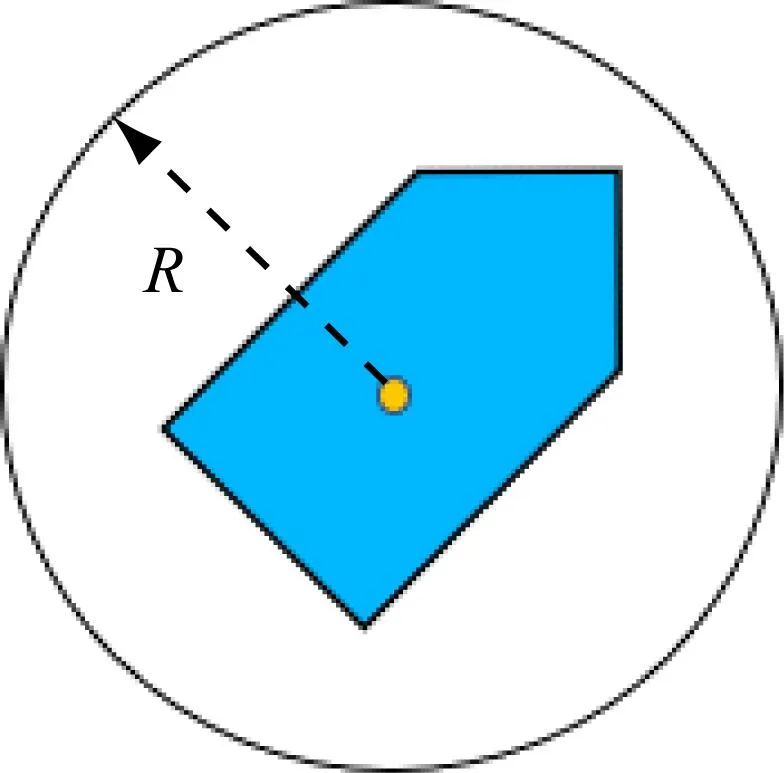
图3 USV的安全区域

式中:di为路径与第i个障碍物之间的距离。若di≤R,则USV的安全区域受到障碍物的侵犯,此时C被赋值为无穷大,规划路径被视为不可行路径。

3 PSO算法

PSO算法是一种基于群体的启发式优化算法[15]。假设在D维空间内存在N个粒子,粒子i在D维空间内的位置和速度分别为xi=(xi,1,xi,2,…,xi,D)和vi=(vi,1,vi,2,…,vi,D)。在迭代过程中,由粒子i的最优位置pi,best=(pi,1,pi,2,…,pi,D)和群体的最优位置gbest=(pg,1,pg,2,…,pg,D)决定粒子i下一步的运动。粒子i的速度和位置的更新公式为

式中:i=1,2,…,N;d=1,2,…,D;t为迭代次数;w为惯性权重;r1、r2为[0,1]内的随机数;c1、c2为加速因子;vi,d,t、xi,d,t、pi,d,t分别为第t次迭代中粒子i的速度、位置、最优位置的第d维分量;pg,d,t为第t次迭代中群体最优位置的第d维分量。

4 EOBL-APSO算法

设计一种自适应惯性权重来平衡PSO算法的全局和局部搜索能力;采用EOBL策略生成由精英个体产生的反向解组成的新种群,提高种群多样性,降低算法陷入局部最优的概率,提高算法精度。

4.1 自适应惯性权重

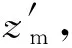
w=

(11)

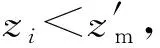
4.2 EOBL策略

PSO算法的不断迭代会降低种群的多样性,故引入EOBL策略来产生新的粒子群,增加种群的多样性和搜索能力。反向学习是TIZHOOSH基于现实世界中事物之间的对立关系提出的解决优化问题的有效方法。对于没有先验知识的优化问题,利用相反的候选解比随机解达到全局最优的概率更高。在PSO算法迭代过程中,如果同时检测到当前解和相反解,则选择更好的解作为预测解,增强算法脱离局部最优解的能力,提高算法的搜索效率。反向学习的定义如下:

定义1反向数。假设一个实数x∈[a,b]且x∈R,则x的反向数定义为

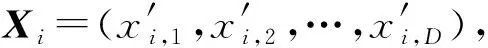
ad=minxi,d,bj=maxxi,d

本文在改进PSO算法中融入EOBL策略来提升改进算法的性能,在每次迭代过程中将目标函数值最小的粒子作为精英个体,并基于该精英个体进行反向学习,生成由精英个体产生的反向解组成的新种群,参与进化竞争。

4.3 EOBL-APSO算法步骤

步骤1创建海域环境地图并初始化环境参数以及USV的起始位置和目标位置。

步骤2初始化粒子的位置和速度,设置参数值,包括种群规模N、空间维度D、最大迭代次数Tmax、最大惯性权重wmax、最小惯性权重wmin、加速因子c1和c2。

步骤3根据式(6)计算粒子当前的目标函数值,按照目标函数值划分粒子,并根据式(11)求得每个粒子对应的惯性权重。

步骤4根据式(9)和(10)更新粒子的速度和位置,根据式(6)计算粒子当前的目标函数值,选择目标函数值最小的粒子作为精英个体,采用EOBL策略生成精英个体的多个反向解组成新的种群,计算新种群中粒子的目标函数值。

步骤5比较精英个体生成的种群与其父代种群的目标函数值,选择更优的个体组成新种群,从当前种群中确定新的全局最优值。

步骤6判断算法是否达到最大迭代次数:若满足则停止搜索,输出USV的全局最优路径;否则返回步骤3继续迭代。

5 仿真结果与分析

5.1 EOBL-APSO算法的性能测试

为评估EOBL-APSO算法的求解精度和收敛性,采用4个标准测试函数(见表1),并与线性递减惯性权重(linear decreasing inertia weight, LDIW)PSO算法[16](记为LDIW-PSO算法)、SA-PSO算法[17]和EOBL-PSO算法[7]进行比较。所有算法的参数设置相同:N=50,w∈[0.40,0.95],c1=c2=2,Tmax=500。

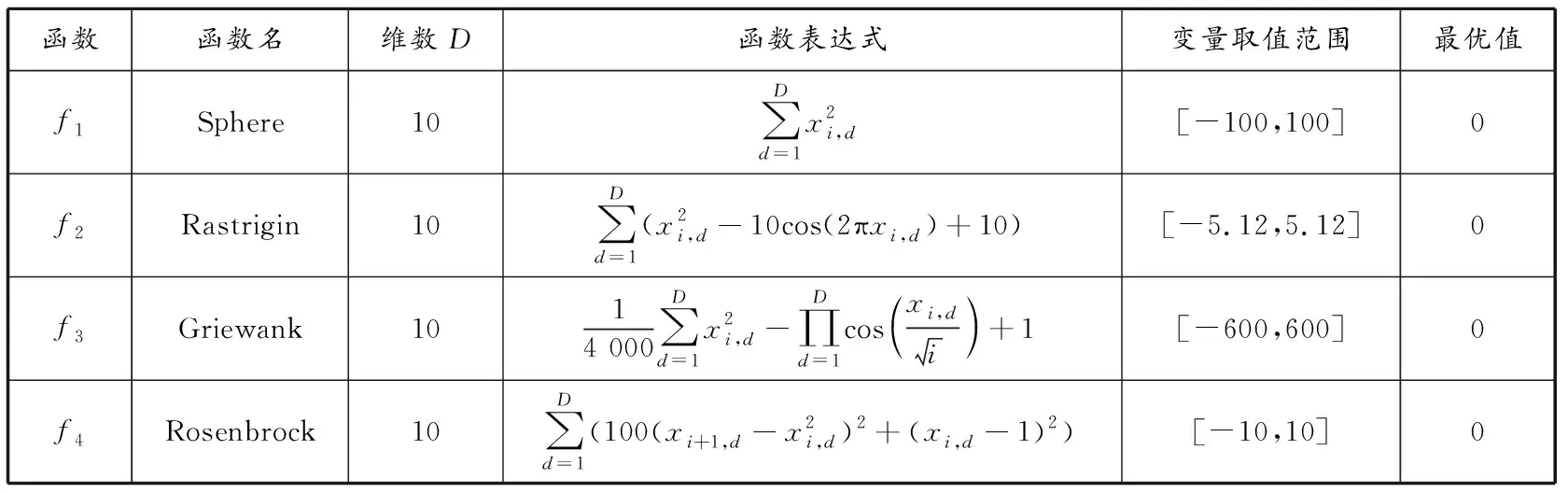
表1 标准测试函数

为避免由偶然性带来的结果偏差,对每个标准测试函数分别进行50次实验,统计并计算出最优值、平均值和标准差,结果见表2。

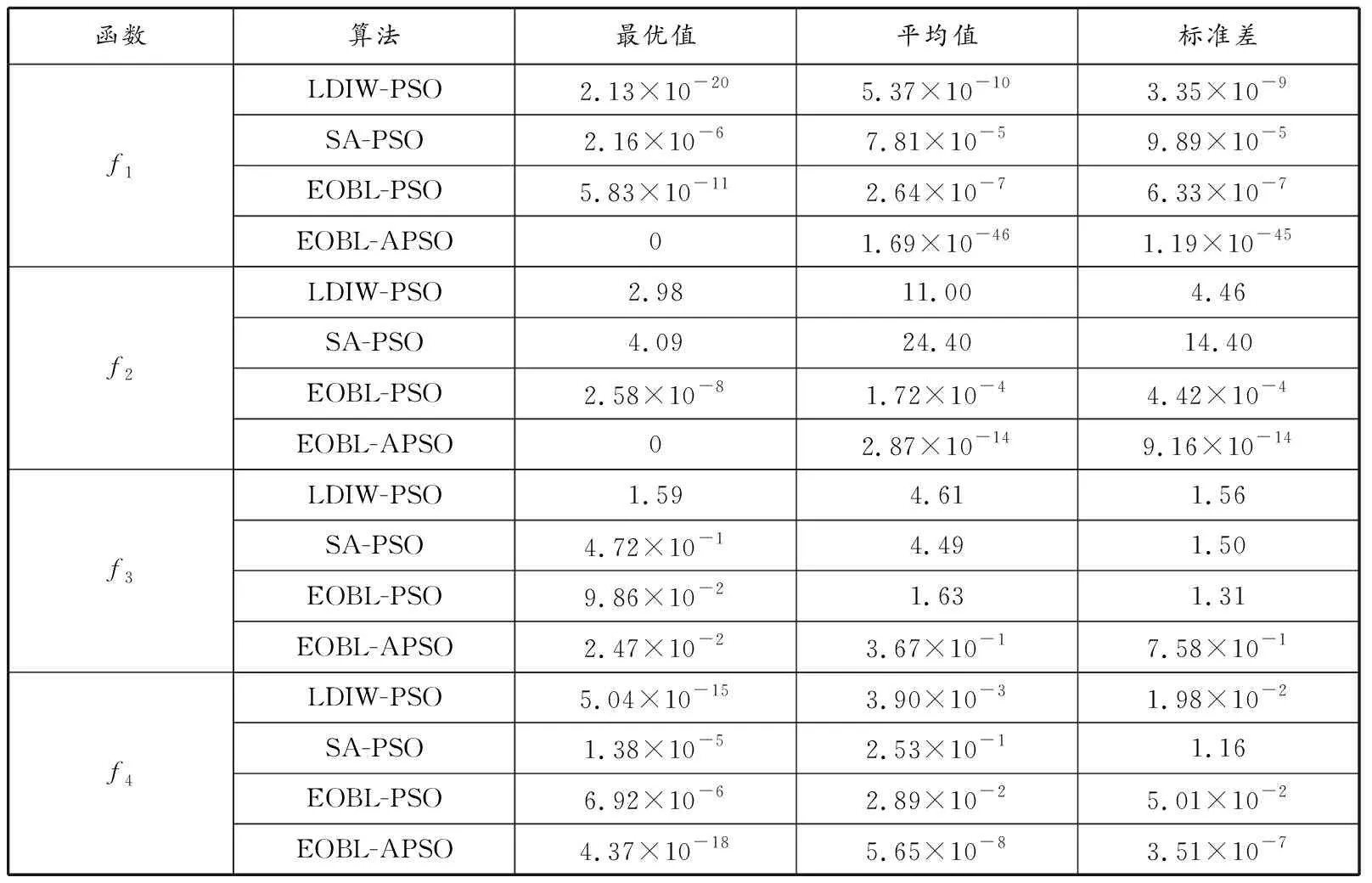
表2 测试函数实验统计结果

由表2可知:对于这4个标准测试函数,本文所提出的EOBL-APSO算法的最优值优于其他算法的最优值,说明EOBL-APSO算法具有更好的求解精度和收敛性;EOBL-APSO算法的平均值和标准差也优于其他算法,说明EOBL-APSO算法具有更好的稳定性。

5.2 多目标标准化因子的确定

在多目标优化函数中,L、E、F具有不同的数量级。为平衡它们对路径选择的影响,必须设置合理的标准化因子。本文采用文献[18]的方法确定各单目标的标准化因子。假定得到的路径都是无碰撞路径,即C=0。分别将ω1、ω2、ω3设为1、0、0,得到单目标L下的最优值Lmin=17.04;分别将ω1、ω2、ω3设为0、1、0,得到单目标E下的最优值Emin=90.96;分别将ω1、ω2、ω3设为0、0、1,得到单目标F下的最优值Fmin=26.14。基于Lmin计算各目标的标准化因子,得到ω1=Lmin/Lmin=1,ω2=Lmin/Emin=0.19,ω3=Lmin/Fmin=0.65。根据得到的各目标标准化因子,计算得到多目标下L、E、F的最优值分别为17.12、17.91和17.43。这3个目标函数值具有相同的数量级且差异很小,有利于路径综合评估。

5.3 海流环境下的路径规划仿真

选择2种海流环境进行模拟并与PSO算法进行比较分析。第一种为固定海流环境,由随机障碍物和具有固定速度和方向的海流组成;第二种为时变海流环境,由多个黏性Lamb涡流叠加形成的海流和随机障碍物组成。本文参数都为无量纲量;海域大小为20×10,横坐标和纵坐标范围分别为[-10,10]和[-5,5];海流以带箭头的线段表示,箭头方向为海流的方向,线段长短表示海流的大小;黑色圆为障碍物。

5.3.1 固定海流环境

海流速度为2,海流方向与x轴方向的夹角为30°。圆形障碍物的集合为{((xobs,yobs),robs)},包括((-8.8,-2.5),1.3)、((0,-2.0),1.3)、((4.0,2.3),1.5)、((-4.0,-2.3),1.5)、((7.0,-2.3),1.4),其中(xobs,yobs)和robs分别为障碍物的圆心坐标和半径。USV的速度为2,起点为(-5.0,-4.0),终点为(8.9,4.0) ,USV发动机的额定功率P=4。N=50,w∈[0.40,0.95],c1=c2=2,Tmax=200。

图4给出了2种算法在固定海流环境下的路径规划结果。由图4和表3可以看出:2种算法在固定海流环境下都能规划出一条无碰撞的路径,并且由于设定了USV的安全区域,规划的路径都能够远离障碍物,保证了航行安全;EOBL-APSO算法的搜索性能较优,规划出的路径在路径长度、能耗和路径平滑度上都优于PSO算法。

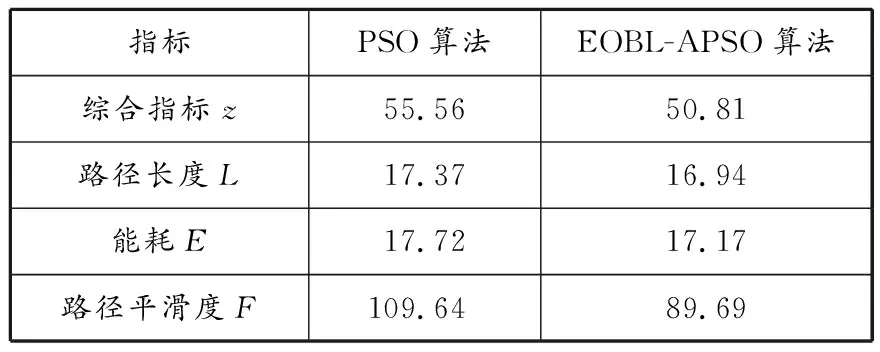
表3 2种算法在固定海流环境下规划出的最优路径评价指标对比

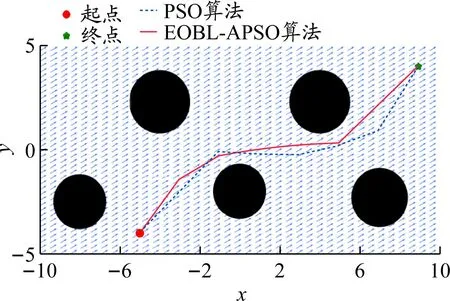
图4 2种算法在固定海流环境下的路径规划结果

5.3.2 时变海流环境

时变海流由4个黏性Lamb涡流叠加形成,涡流强度H=20,涡流半径δ=1。USV起点为(-9.5,4.0),终点为(4.0,-3.2)。圆形障碍物设置及其他参数不变。

图5给出了2种算法在时变海流环境下的路径规划结果。由图5和表4可以看出:2种算法在时变海流环境下都能规划出一条无碰撞且远离障碍物的安全路径;EOBL-APSO算法规划出的路径能够较好地沿着海流的方向,因此在能耗上优于PSO算法,且路径更平滑,路径长度也优于PSO算法。从整体仿真结果看,本文对PSO算法的改进具有明显的效果,改进算法能够更好地对多目标进行平衡,从而得到更好的全局最优路径。

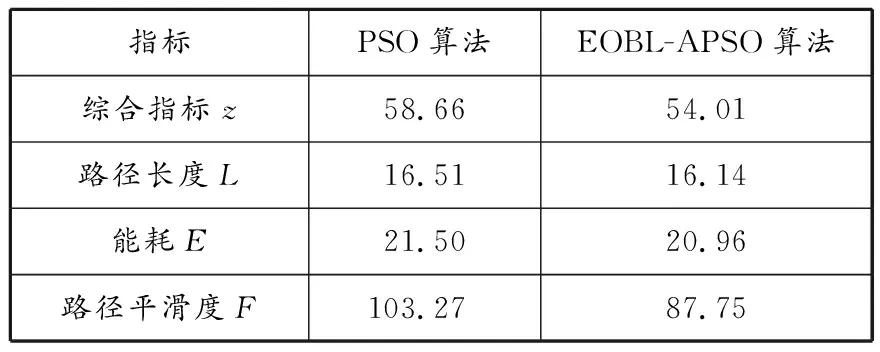
表4 2种算法在时变海流环境下规划出的最优路径评价指标对比

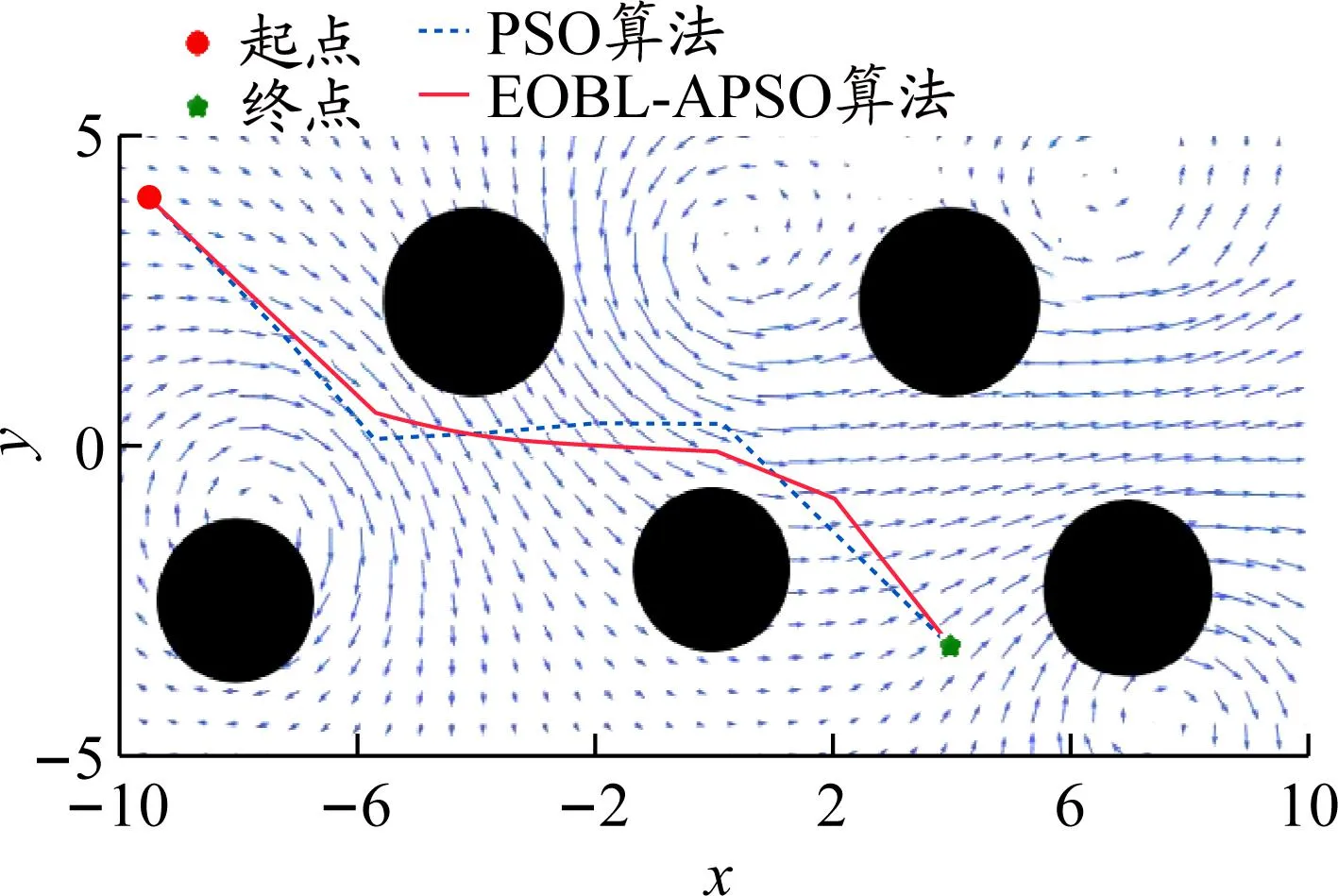
图5 2种算法在时变海流环境下的路径规划结果

5.4 实际海域环境的仿真

将本文所提出的方法应用于实际海域环境下的路径规划。选取宁波舟山港条帚门航道附近的海域构建仿真环境。基于该海域的全景地图构建200×200像素的海域环境模型,并且利用Lamb涡流模型构建该海域的海流场。

图6显示了该海域的路径规划结果:路径与障碍物保持一定的安全距离;规划路径避开了逆流,顺着海流的方向,减少了USV的能耗;兼顾了其他优化目标,满足USV的全局路径规划要求。

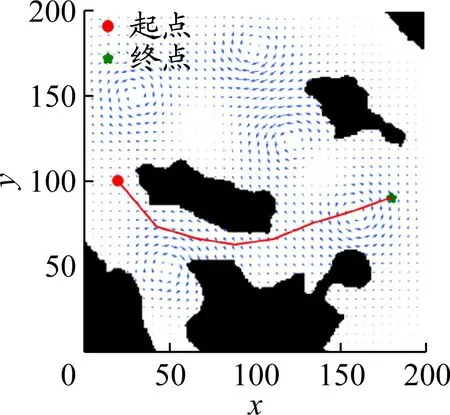
图6 条帚门航道附近海域的路径规划结果

6 结 论

针对海流环境下无人水面艇(USV)的多目标路径规划问题,综合考虑了路径长度、能耗和路径平滑度等3个优化目标以及障碍物和海流的影响,构建了USV多目标路径规划模型,并且提出了一种改进的粒子群(PSO)算法进行求解。在2种不同的海流环境以及实际海域环境下进行路径规划,结果表明改进算法能够优化多个目标,规划出一条最优路径。通过与不同算法的比较,验证了改进算法具有良好的鲁棒性和适用性。