车载危爆品爆炸作用下桥面压力场分布及破坏效应研究*

熊红霞,曾 珍,胡志坚

(1.武汉理工大学 土木工程与建筑学院,武汉 430070;2.武汉理工大学 交通学院,武汉 430063)

近年来由于车载危爆品爆炸事故时有发生,一旦车载物在桥梁上发生意外爆炸,会导致桥梁损伤破坏甚至倒塌,造成重大经济损失或人员伤亡。如2013年连霍高速公路义昌大桥烟花爆炸垮塌事故[1];2022年,俄罗斯重要基础设施克里米亚大桥发生油罐车爆炸袭击,造成部分桥段垮塌;2022年,缅甸仰光至土瓦的一座桥梁被定点炸断,物资运输中断。因此,研究桥梁在爆炸冲击荷载作用下的动力响应及破坏特征,用于指导桥梁在防爆抗爆方面的安全防护设计,具有重要的理论和现实意义。

目前已有众多学者在进行工程结构领域的防爆抗爆性能研究工作[2-12]。但现有研究主要集中在建筑物爆炸和大型空间结构室内爆炸方面,关于桥梁结构在爆炸荷载作用下的相关研究不多,国内外的桥梁规范均未单独考虑爆炸荷载的影响,对其取值标准尚缺乏具体规定。Han G等通过试验对预应力 T型梁桥钢筋及T梁腹板的破坏演变形态、裂缝发展、残余承载力等进行了研究[2];胡志坚等针对大跨径混凝土斜拉桥的动力响应和不同爆炸作用工况下的损伤破坏进行了研究[3];Williams 等制作了钢筋混凝土高桥墩模型[4],研究细长 RC 柱保护层在爆炸中剥落的损伤机理;Liu H等通过缩尺试验[5],对比分析了1个整体式桥墩和12个预制节段式桥墩在近距离爆炸荷载下的破坏模式,发现节段数、长细比、截面几何形状等因素会影响桥墩局部残余变形和预应力损失。随着区域经济的协同发展,资源与能源量交换频繁,公路上装载运输“燃、汽、爆、化”的危爆品货车数量日益增多。研究车载危爆品在桥面近场爆炸时的冲击波压力场分布规律及对桥梁的破坏效应,深入探讨车厢钢板阻挡等因素对桥面超压峰值荷载场的影响是非常有必要的。

1 桥面车载危爆品爆炸的数值模拟

1.1 爆炸力学模型的建立

以一座实桥——凤排桥遭遇的车载爆炸事故为实际工程背景。参考其灾后损伤检测报告,借助ANSYS AUTODYN动力学软件,建立了考虑车体钢板影响作用的桥面车载物爆炸力学模型,分析炸药量、起爆位置、车体钢板等因素对爆炸冲击波传播的影响,判断钢板产生阻挡效应的范围。空气、炸药、混凝土、梁体、钢板等主要材料的状态方程如下。

(1)空气状态方程,视空气为理想气体,表达如下

P=(γ-1)ρe

(1)

式中:材料常数γ=1.4;空气密度ρ=1.225 kg/m3;初始比内能e=2.068×105kJ/kg。

(2)混凝土状态方程

混凝土是以RHT模型为基础的,RHT模型综合考虑了应变硬化、软化、损伤和应变率效应的影响,其状态方程如下

p(ρ,E)=A1μ+A2μ2+A3μ3+(B1μ)ρ0e

(2)

式中:μ=(ρ/ρ0)-1为材料体积变化的相关参数;A1、A2、A3、B0和B0为常量,数值待定;ρ0表示初始密度;e表示内能。

(3)按JWL方程表达炸药状态方程

(3)

式中:P为爆炸压力;E为炸药内能;V为当前炸药相对体积;A、B、R1、R2和ω为材料参数。根据材料参数取值。

(4)钢筋状态方程

钢筋状态方程以Johnson-Cook模型为基础[9,10]

(4)

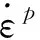
爆炸力学模型基本尺寸及参数设置:桥梁横宽12 m,纵长20 m,桥面板厚0.9 m,在桥面板上方1.2 m高度加设6 cm厚度的钢板结构(模拟车厢四周钢板对爆炸冲击波的阻挡),取车厢底板位于桥面中心(如图1所示)及1/4处作为两个起爆位置。炸药及空气用Euler单元模拟;钢板与梁体结构用Lagrange六面体单元模拟;各材质界面间采用Euler-Lagrange进行耦合;根据精度需要划分变形区域的网格尺寸。桥面上沿纵横两个方向布设了273个(21×13)测点,间距均为1 m,实时记录各测点处爆炸冲击波超压峰值的数据变化。

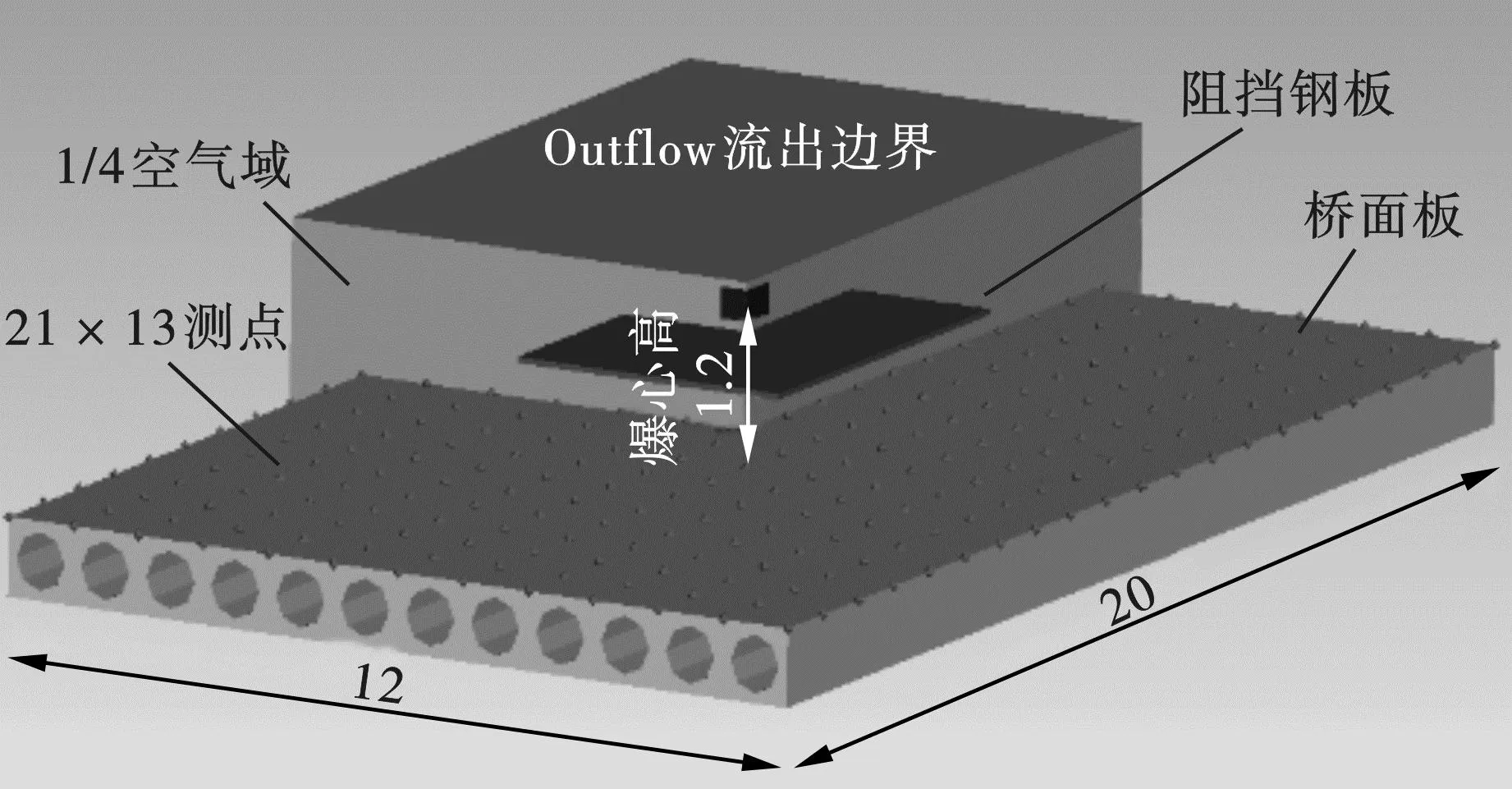
图1 力学计算模型(单位:m)Fig. 1 Finite element models(unit:m)

1.2 爆炸力学模型精度验证

为验证所建立的爆炸力学模型的精度,准确模拟爆炸波的传播过程及其与桥梁结构的相互作用,需找到合适的参数取值、网格尺寸和有效的算法以保证计算精度。因此,先建立了一个450 kg TNT炸药在桥面板上方1.2 m高处爆炸的数值模型,分别将网格尺寸取为20、50、100、200(单位均为mm),来进行数值试验验证。试算过程中发现,当爆炸比例距离较小(Z≤0.8 m/kg1/3)时,桥面冲击波超压的数值模拟值对网格尺寸变化较为敏感,宜选择网格尺寸较小的单元;当比例距离Z≥1.0 m/kg1/3时,计算结果对网格尺寸的敏感性较弱,可以选择较大的网格尺寸。本文数值模拟的比例距离范围为0.03～1.3 m/kg1/3,与前人的经验公式[炸药在刚性地面上爆炸时的Baker公式和炸药在无限空气中爆炸时的Henrych(1979)公式]进行了对比[9,10],结果如图2所示。

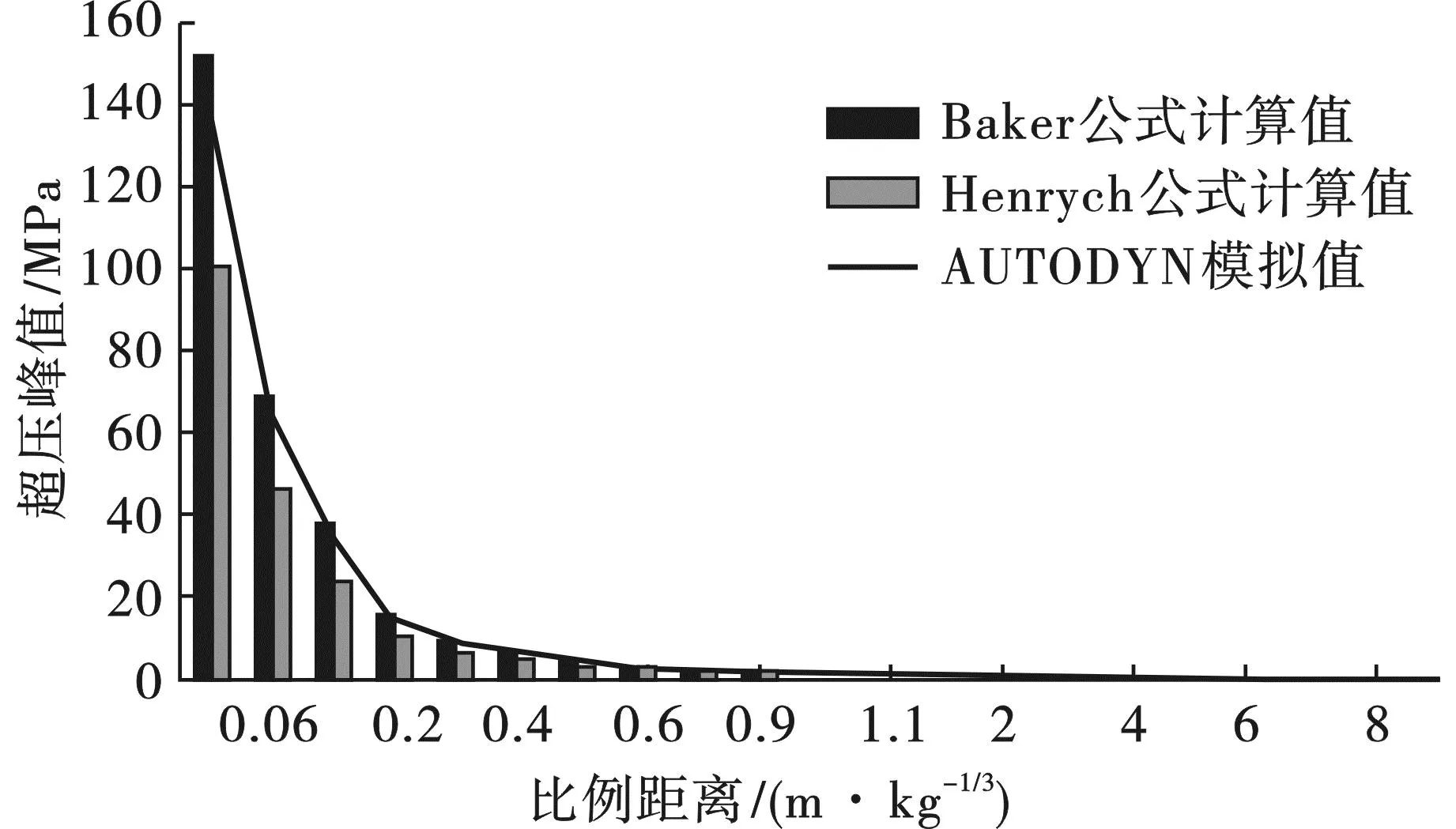
图2 数值模拟结果与经验公式结果对比Fig. 2 Comparison of overpressure between simulation values and empirical formula

从图2可知,当爆炸比例距离Z在0～0.5 m/kg1/3之间时,数值模拟值与Baker公式计算值较为接近;当Z>1m/kg1/3时,数值模拟值与经验公式计算值几乎重合。据此验证了力学计算模型和参数取值的合理有效性。

2 车体钢板对桥面冲击波压力场分布的影响

2.1 钢板阻挡作用下桥面爆炸冲击波的传播

空气冲击波是一种高压气浪,它的冲击力和运动速度都非常高。当冲击波在传播过程中遇到小尺寸障碍物(如此处的钢板)阻挡时,会发生反射、绕射作用,钢板两侧同时产生环流现象。当两侧环流波绕到钢板后方继续传播时会发生集聚碰撞现象,在离爆心下方有一定距离的桥面上不断聚集加强,并形成压力较大的合成波区,该桥面区域的破坏程度会更严重。

图3(a)～(d)展示了冲击波传播与车厢钢板阻挡形成环流效应的典型过程。图3(a)所示,在t=0.021 ms,爆炸发生后释放出大量热能和气体爆轰产物,产物膨胀压缩其周围空气产生爆炸波,以爆点为中心,呈球面波的形式向四周扩散传播;图3(b)所示,冲击波遇到车厢钢板产生碰撞,气流运动被钢板遏制,钢板上方的反射冲击波压力迅速增大,形成高压反射区;图3(c)所示,传播未遇阻碍的冲击波在钢板侧面产生环流效应,钢板上方的高压区气流往钢板两侧边缘外的低压区流动,高压区空气逐渐稀释形成稀疏波;图3(d)所示,阻挡钢板出现下挠现象,说明钢板起到了一定的消能作用。环流超压绕钢板两侧传播到某处桥面板后,压力急剧升高,使该处桥面受到巨大的冲击破坏作用。

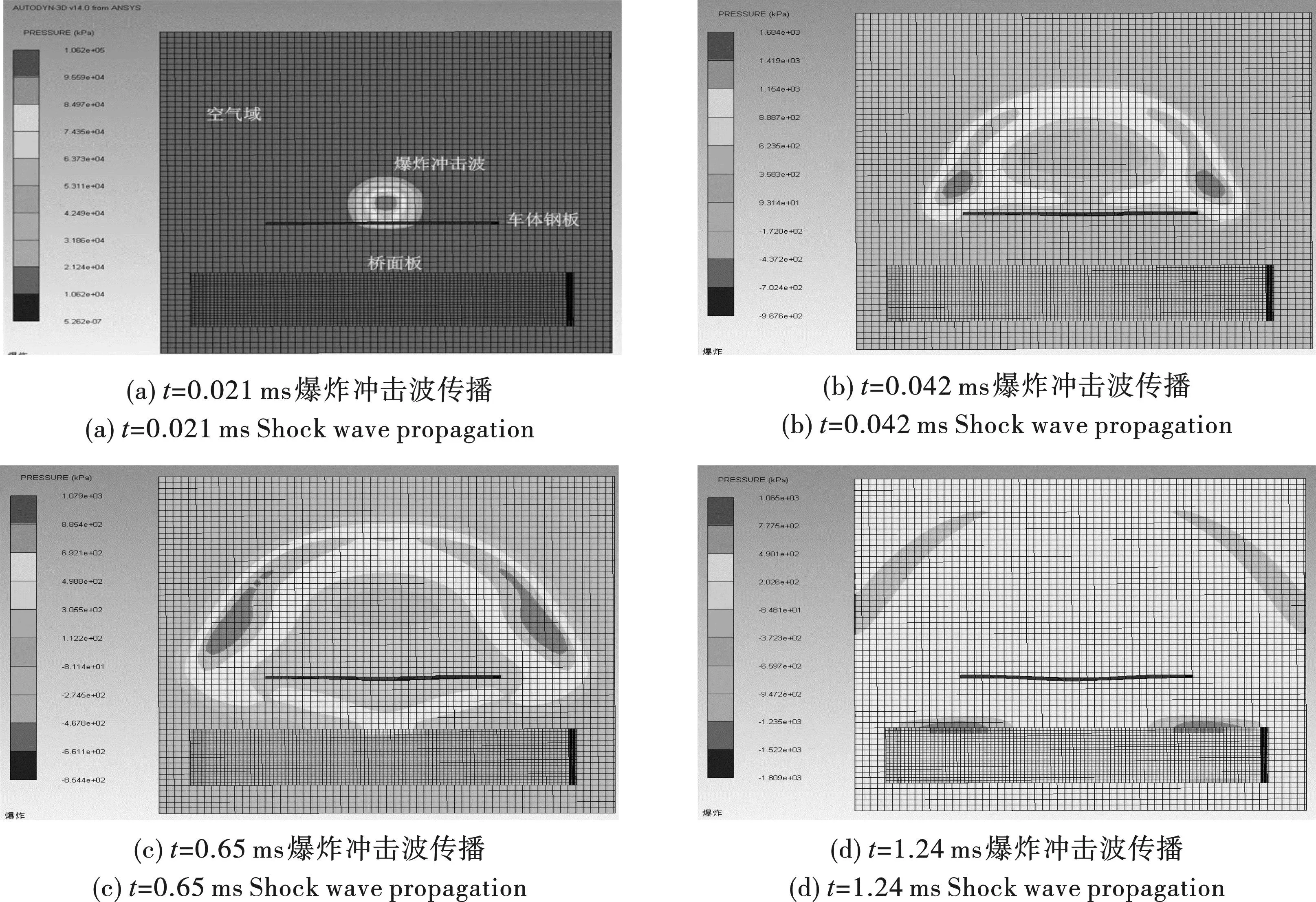
图3 爆炸冲击波传播过程Fig. 3 Blast wave propagation process

2.2 钢板阻挡作用下桥面超压峰值荷载场的分布

根据前述分析结果,车厢底部钢板影响了桥面爆炸冲击波的传播规律。公路上运输易燃易爆品车辆发生交通事故引发爆炸具有很大的随机性,导致了爆炸荷载压力场分布的不确定性。为了探讨车体钢板对桥面冲击波压力场分布的影响,设计了在其它因素一致的情况下不考虑钢板阻挡(工况一)和考虑钢板阻挡(工况二)的两种爆炸工况。按两种工况模拟计算后提取桥面同区域范围多个代表性点位的超压峰值进行对比。图4～图5对比分析了两种工况的超压峰值荷载场分布情况。

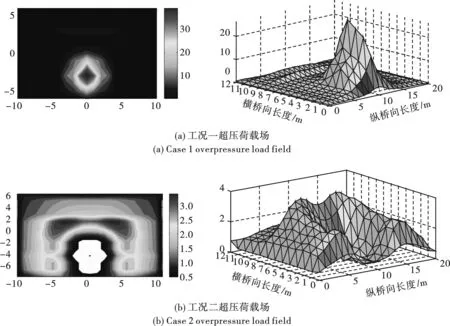
图4 两种工况超压峰值荷载场分布Fig. 4 Overpressure field of different cases

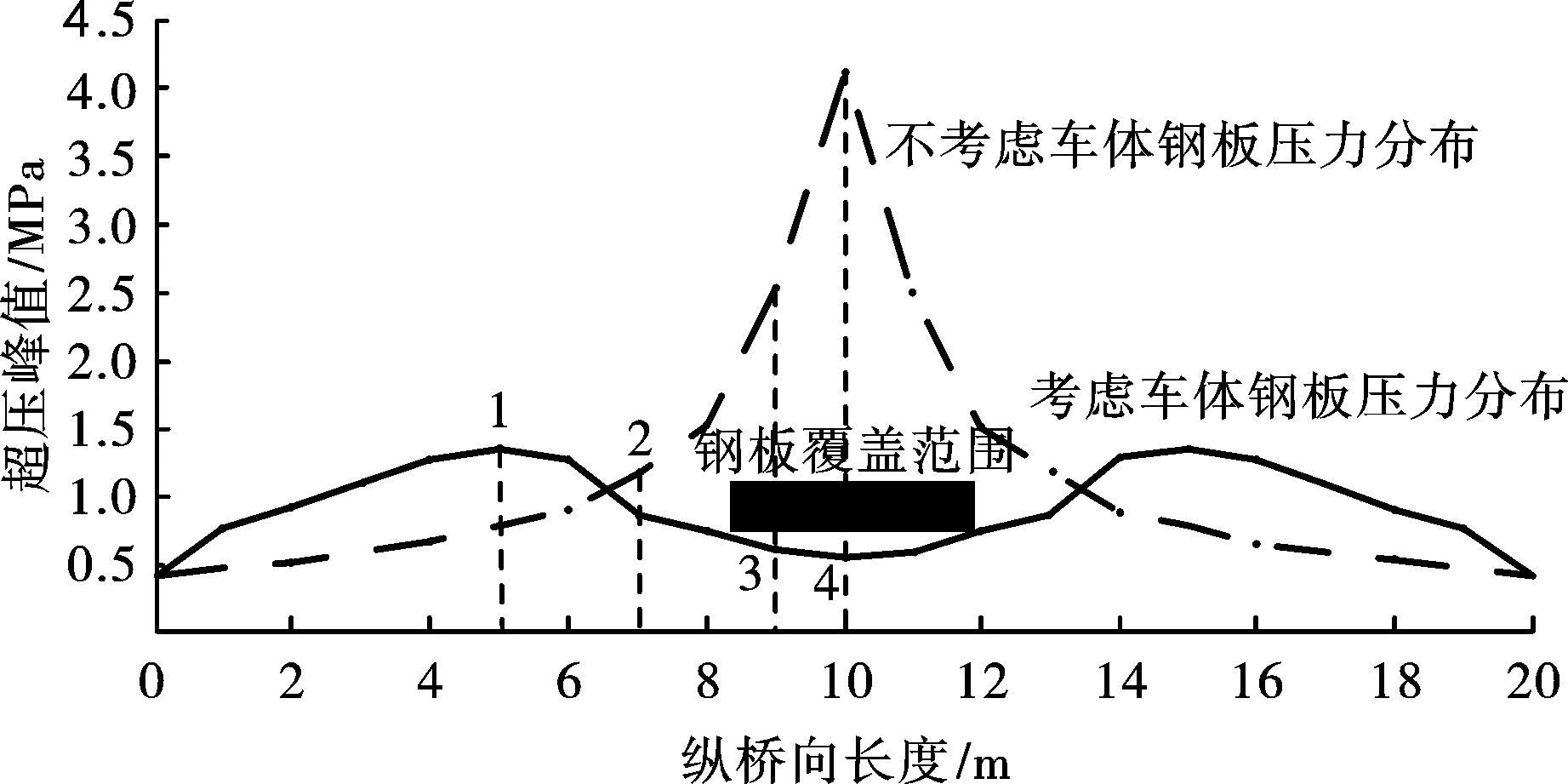
图5 两种工况沿纵桥向不同距离处超压峰值分布Fig. 5 Peak overpressure along longitudinal bridge of different case

工况一如图4(a)所示,不考虑钢板阻挡时,荷载冲击波高压区域的峰值作用范围特别集中,且超压峰值很大;工况二如图4(b)所示,设置钢板时,在钢板阻挡作用下,超压峰值出现明显的削峰现象,且荷载高压区的分布范围沿钢板四周向外扩散。桥面特定区域对比可看出,在横桥向7～11 m长度范围内,无阻挡钢板时超压峰值要远超有阻挡钢板的情形。此区域内沿纵桥向一定距离范围内的典型点位超压峰值曲线如图5所示。

选取图5中分别位于钢板覆盖区域内外的1～4几个代表性点位,提取其冲击波超压时程曲线如图6所示,有钢板阻挡时,一部分冲击波与钢板相遇后发生反射,追上后一波传来的入射波,与之叠加,相互作用形成合成冲击波,其传播出现延时现象;且钢板覆盖区内的测点均有二次超压现象;阻挡钢板覆盖区以外,部分位置的冲击波反而比无钢板阻挡时破坏作用更强。

图6 典型点位处超压时程曲线Fig. 6 Time-history curves of overpressure of representative points

3 车载危爆品爆炸作用下桥面超压峰值预测

3.1 桥面超压峰值预测公式的提出

目前国内外关于爆炸冲击波超压值的计算已有一定的经验公式及预测方法,但普适性的经验公式更适用于炸药在无限空中爆炸或在地面上爆炸等情形,一般假定反射面为无穷大。根据前文分析,车载危爆品爆炸时,车厢钢板改变了桥面压力场的分布形式,自由空气域的超压预测经验公式已不适用。

鉴于前文在研究车载物爆炸荷载场分布时,通过一定数量的数值算例分析,得到了桥面板荷载超压分布的规律,现考虑对前人的经验公式进行修正,提出一个适用于车载爆炸物在桥面一定高度处爆炸的荷载冲击波计算公式。本文基于Baker公式理论知识,利用MATLAB中的polyfit(x,y,n)函数,用最小二乘法对仿真数据进行多项式曲线拟合,用最高次数为n次幂的函数来拟合y与x的关系,得到了考虑车体钢板影响作用的桥面超压峰值预测公式

(5)

式中:P为车载物爆炸时桥面上的冲击波峰值超压值,MPa;Z为比例距离,是爆炸中心的距离与爆炸药量的立方根之比,m/kg1/3。

3.2 桥面超压峰值的计算

为验证本文提出公式的有效性与计算精度,分别用上面提出的公式和数值模拟仿真两种方法对桥面不同区域的爆炸荷载压力值进行计算分析。

图7所示为本文提出的公式计算的爆心距横桥向内侧分别为2 m和6 m区域内沿纵桥向不同点位处的冲击波超压峰值。图8所示为数值模拟、传统经验公式及本文提出公式三种方法得到的桥面冲击波超压峰值对比。从图8可看出,本公式计算的结果与数值模拟的结果非常吻合,但二者与Baker公式计算值相差较大,说明适用于空气域中直接爆炸的超压预测经验公式已不适用于本文研究的爆炸情形。

图7 桥面不同位置压力分布线图Fig. 7 Pressure distribution along transverse direction of bridge

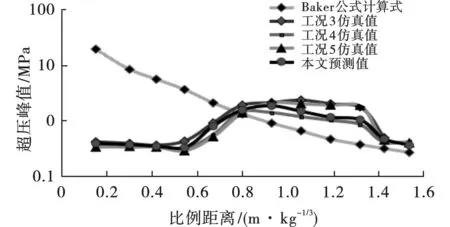
图8 桥面板预测超压峰值Fig. 8 Prediction of pressure on the bridge

4 桥面车载爆炸事故反演

2009年,一辆装载烟花的货车和另一辆装载黄油的货车行驶在凤排桥西线时,因追尾碰撞发生爆炸,导致西线第4跨结构出现严重损坏。因爆炸源车辆已完全炸毁,车厢钢板尺寸尚不明确。本文根据常见危险品运输车辆的型号参数,考虑车体钢板形状、厚度、表面尺寸等参数变化对桥面压力分布区域的影响,设置了工况三、四、五,见表1所示,以此推演还原凤排桥在车体钢板阻挡作用下的车载物爆炸情形[2-8]。炸药量取450 kg立方体TNT炸药,5 t载重量货车,车厢底板距桥面高度设为1 m,爆心高度按炸药堆的几何中心取为1.2 m,单点起爆。图9为爆炸车辆平面示意图,图10为爆炸位置示意图。因货车护栏较高、挡板全封闭时,钢板对爆炸冲击波的实际阻挡作用有所增强,故仿真车厢底板尺寸较实际车厢(2.4 m)稍有加宽。

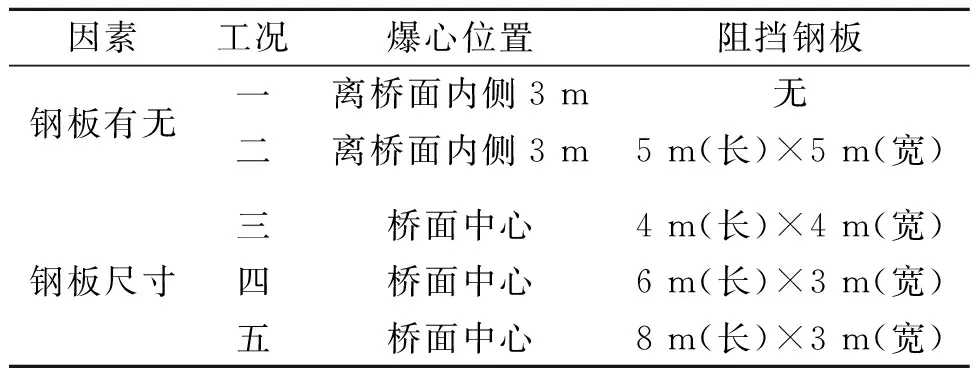
表1 爆炸工况及参数设置Table 1 Parameters of 8 load cases

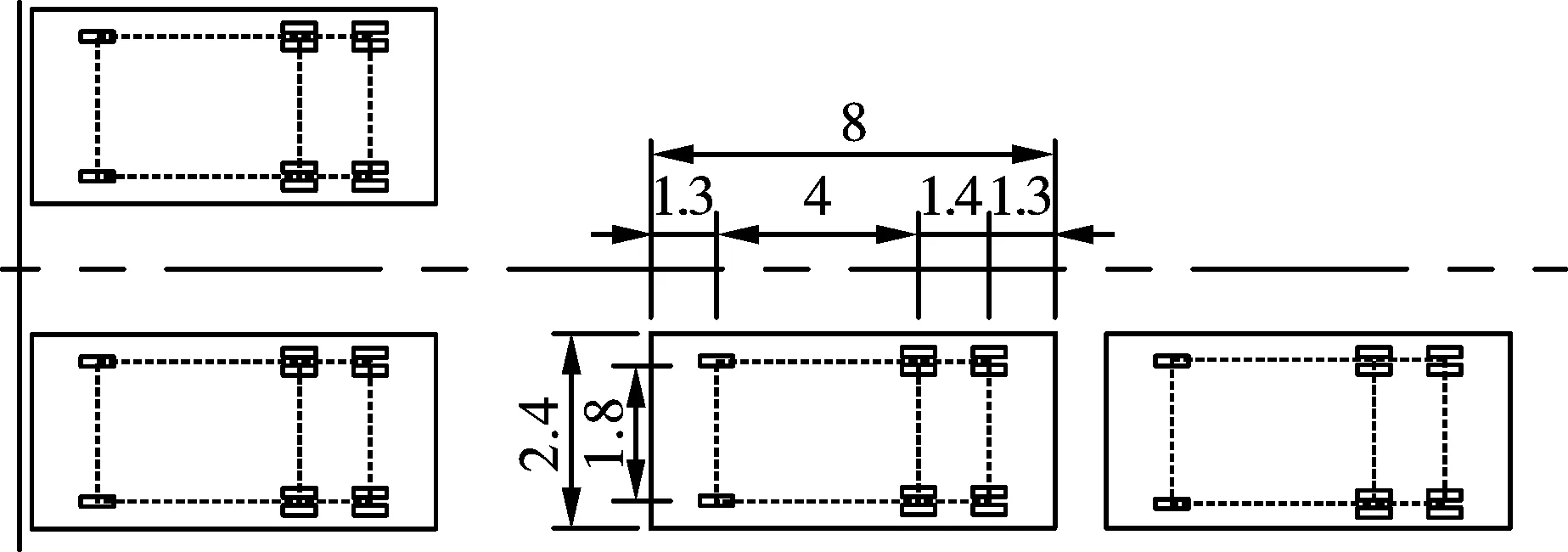
图9 爆炸车辆平面布置图(单位:m)Fig. 9 Layout of the exploded vehicle(unit:m)

图10桥梁横截面及爆炸位置图(单位:m)Fig. 10 Bridge cross-section and explosive positions(unit:m)

图11所示为工况三和工况五数值模拟得出的桥面超压峰值等高线分布情况。从图中可观察到,车厢钢板对覆盖区域的冲击波起到明显阻挡作用,板侧环流效应使桥面压力场产生重分布,非钢板覆盖区域超压值显著提高。

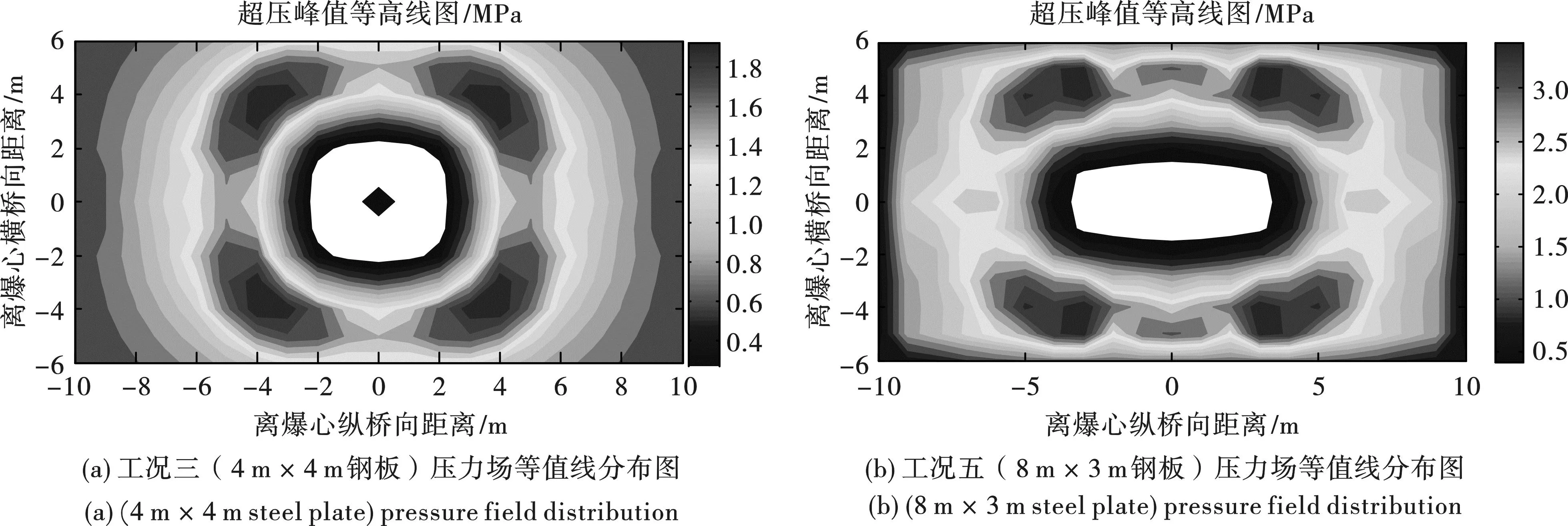
图11 不同工况下压力场分布图Fig. 11 Effect of steel size to pressure distribution

根据钢板对桥面荷载压力场的影响,可将钢板覆盖范围内的荷载场划分为四个区域:

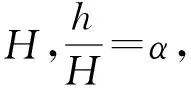
(6)

若钢板形状是边长为b的正方形,冲击波隔离区近似于图11(a)所示的圆形;若钢板平面为长度l、宽度b的长方形时,冲击波隔离区形状为图11(b)所示的椭圆形,其圆心为爆心在桥面板的投影。

Ⅱ.爆炸荷载衰减区:该区域冲击波因钢板阻挡呈现衰减现象,位置距离爆心越近,其衰减效应就越明显。

Ⅲ.爆炸荷载增强区:此区域超压峰值较大,冲击波集聚明显。

Ⅳ.爆炸荷载不变区:此区域远离爆心位置,几乎不受到钢板阻挡作用的影响。

为探求不同形状、厚度、尺寸的钢板对隔离区域的影响规律,通过改变车厢钢板尺寸观察桥面超压峰值区域的变化。图12所示为长、宽、高分别为4.2 m×2.4 m×0.06 m钢板和8.0 m×2.4 m×0.06 m两种钢板阻挡下的桥面超压峰值等值线图。图中红色虚线为车厢钢板所在位置,冲击波隔离区长度随钢板长度增加而增加,钢板表面积越大,隔离区范围也越大,随着钢板长度、宽度增加,压力场接近于零的区域也相应增加。当钢板边长在h～2h(h为爆心高度)之间时,钢板消峰阻挡作用随着钢板尺寸增大逐渐明显,方形钢板边长为1.5h～1.8h时,钢板下方超压值衰减最快。图13所示为车体钢板的应力分布图,爆炸初始时刻,钢板正面中部应力值分布较大,随着冲击波迅速传播后,板底面形成应力集中,瞬间产生严重下挠变形,表明车体钢板确实起到了一定程度的耗能消峰作用,避免了爆炸冲击波毫无遮挡地直接作用于下方的桥面。

图12 两种钢板大小的超压峰值等值线图Fig. 12 Peak overpressure for two steel plate sizes

图13 车体钢板应力分布图Fig. 13 Stress distribution of steel plane

5 实桥爆炸检测报告与数值分析结果对比

根据凤排桥碰撞爆炸事故检测报告,西-4-span1#梁跌落,2#～7#梁下挠严重,桥面沥青层多处纵向贯通裂缝,与斜向裂缝连通。选取在爆炸荷载作用下损伤破坏较严重的西-4-span桥面板,划分为剪切、弯剪、弯曲等三个破坏区域,分别如图14所示的Zone1区、Zone2区、Zone3区。

图14 桥面板破坏区域示意图Fig. 14 Deck damage for simulation and actual condition

Zone1剪切区虽接近爆炸源,因车厢钢板阻挡作用,该区域破坏并不严重,对应实桥灾后现状,离爆源最近的11#、12#梁未出现明显损坏。值得注意的是,该区域车厢底板下方的爆炸荷载被阻挡后,重新分布于支座附近较小的范围内,支座附件梁体表现为剪切开裂破坏特征,对应实桥破坏情况,9#梁支座处开裂破坏,10#梁底板支点附近出现斜向裂缝,表明在结构抗爆设计中应加强支座附近的抗剪能力。

Zone2弯剪区钢板阻挡效应随比例距离增大而减小,该区域梁体呈现弯剪破坏特征,实桥检测结果显示4#～8#梁出现大量不均匀分布的剪切裂缝和弯曲裂缝。

Zone3弯曲区比例距离较大,车厢钢板的阻挡作用微弱到可以忽略不计,该区对应于荷载场的双峰区域,荷载峰值较大且相对集中,呈现较严重的破坏现象。实桥检测发现,比例距离最大的1#梁脱离盖梁挡块后跌落。2#、3#梁跨中明显下挠,出现大量非均匀分布的弯曲裂缝,如图15(c)所示。表明爆炸荷载主要作用于跨中部位,梁体表现为弯曲破坏特征。

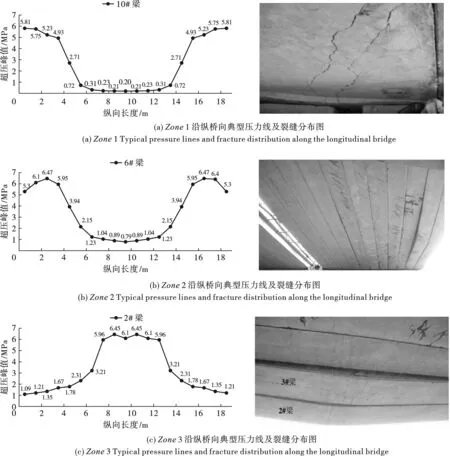
图15 桥面各区域典型压力线图Fig. 15 Overpressure distribution and crack layout on bridge

数值模拟分析桥面损伤各区域以及沿纵桥向的典型压力线分布情况,均与实桥爆炸后检测报告中的裂缝分布情况对应吻合良好,如图15所示。

6 结论

探究了桥梁在遭遇车载危爆品爆炸情况下的冲击波荷载压力场分布规律,提出了考虑车厢钢板阻挡的车载物爆炸作用下桥面超压峰值预测公式。从前述计算分析可得出如下结论:

(1)当桥面上发生车载物爆炸时,车体钢板的阻挡作用会影响爆炸冲击波的传播过程,改变桥面压力场分布形式,使桥面超压荷载峰值出现明显的削峰和延时现象,自由空气域的经验公式不适用于此类爆炸,可以采用本文提出的桥面超压峰值预测公式。

(2)钢板覆盖范围内的桥面荷载压力场可划分为四个区域,钢板尺寸变化对荷载冲击波隔离区域的范围有影响。随着钢板表面尺寸增大,冲击波隔离区范围也增大,钢板覆盖区范围内压力场接近于零的区域也相应增加。今后在危爆物品运输车辆设计中可考虑增大车厢底部钢板的长度、宽度和厚度,加固加高四周的围挡钢板,以减小爆炸波对桥梁结构的直接冲击作用。

(3)基于实桥爆炸事故推演,将桥面板划分为不同的破坏区域,数值模拟得出的各区域典型压力线分布,均与实桥爆炸后检测报告中的裂缝分布及梁体破坏情况对应吻合良好。建议针对货车交通量大的公路桥梁,进行结构防爆抗爆设计时,应着重加强支座附近的抗剪能力和跨中位置的抗弯曲能力。