基于PZT机电耦合效应的工作平台调平方法
2023-12-28徐爱群高津烜王名宏
徐爱群,高津烜,饶 胜,王名宏
(浙江科技学院 机械与能源工程学院,杭州 310023)
在机械零件的加工过程中,使工作平台保持水平十分重要。随着微机电系统的发展,大多数机械设备对水平度的要求越来越高,许多机械设备的工作平台在受力时会发生微小的倾斜,各种误差的累积严重影响成品的品质,因此必须进行水平调节。
传统的位置反馈调平方法所检测的变量是平台的位移量,由于产生的位移是力作用的结果,因此平台的位移较之作用力具有明显的滞后性。关于调平方法的实际工程应用已有大量研究。在提高装置抗冲击性能方面,李琳等[1]针对设备倾斜造成姿势不当等问题,提出了一种对旋转输出轴根部增加圆角和加装橡胶缓冲垫及弹簧支撑件的方法,以降低调平装置受到的冲击应力,提高调平装置的抗跌落性能。在提高调节速度方面,邓传涛等[2]针对平台调平控制,提出了一种结合比例、积分和微分等3种方法于一体的控制算法,相比传统控制算法具有更高的控制精度和动态性能,调节速度提高了40%以上。在模型优化降低误差方面,张强等[3]针对高空作业平台液压调平机构的工作原理进行了研究,对上下调平机构六变量优化的数学模型进行优化,将调平误差最大值降低了49%,上调平液压缸所需最大推力降低了2%。在调平精度方面,冯仪等[4]采用伺服电机控制的四支点支撑平台,设计的系统实现了机电一体化,调平精度结果小于1′,调平时间小于2 min。
综上所述,现有调平方法并不完全适用于微系统和精密机械,应用领域有限,实现成本较高,不能满足精密零件加工对工作平台水平精度的要求;且大多采用四点支撑结构,容易因受力不均而产生“虚腿”现象,造成伺服电机过载[5]。因此,本研究设计了一种等边三支腿调平结构,仿真分析工作平台受力时可驱动支腿的4种受力情况。鉴于以往对压电陶瓷的研究主要集中于材料自身的特性及能量存储方面[6-8],故本研究提出一种基于PZT(piezoelectric ceramics,压电陶瓷)功能材料固有的压电应变属性的调平方法,工作平台的调节根据材料本身的微动位移来实现,避免了液压和电机等介质造成的误差。
1 调平机构工作分析
在无外电场作用时,压电陶瓷表面电畴由于内部的极化作用相互抵消。经过极化处理后,内部电畴自发极化方向都趋于外加电场方向,即呈现压电效应。而压电陶瓷的逆压电效应原理则是压电陶瓷在电场作用下产生极化,在电场力的作用下产生形变[9-11]。
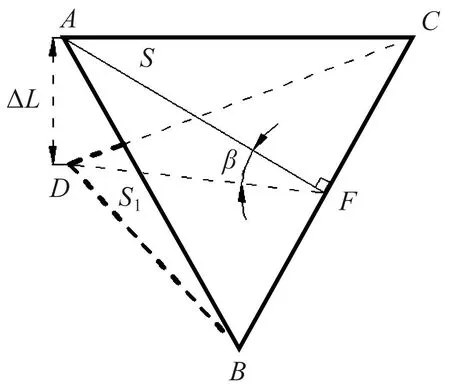
调平机构整体结构主视图见图1,压电陶瓷的局部结构如图2所示。工作平台用于承载工作载荷,俯视呈等边三角形结构。底座和工作平台由3只可驱动支腿通过预紧螺钉连接,呈等边三角形分布。在压电陶瓷的局部结构中,压电陶瓷驱动器、传感器、柔性铰链及电绝缘材料环氧树脂以竖直方向依次排列;传感器用来检测电压,驱动器用来控制支腿的伸缩量,环氧树脂用作驱动器和传感器的绝缘黏结剂。柔性铰链为可驱动支腿提供轴向支撑。由于底座对可驱动支腿的轴向约束,当工作平台受到工作载荷时,支腿的位移量会沿着竖直方向变化,通过对比各支腿分力的大小关系来施加驱动电压控制压电陶瓷的微小形变,从而实现工作平台的调平。
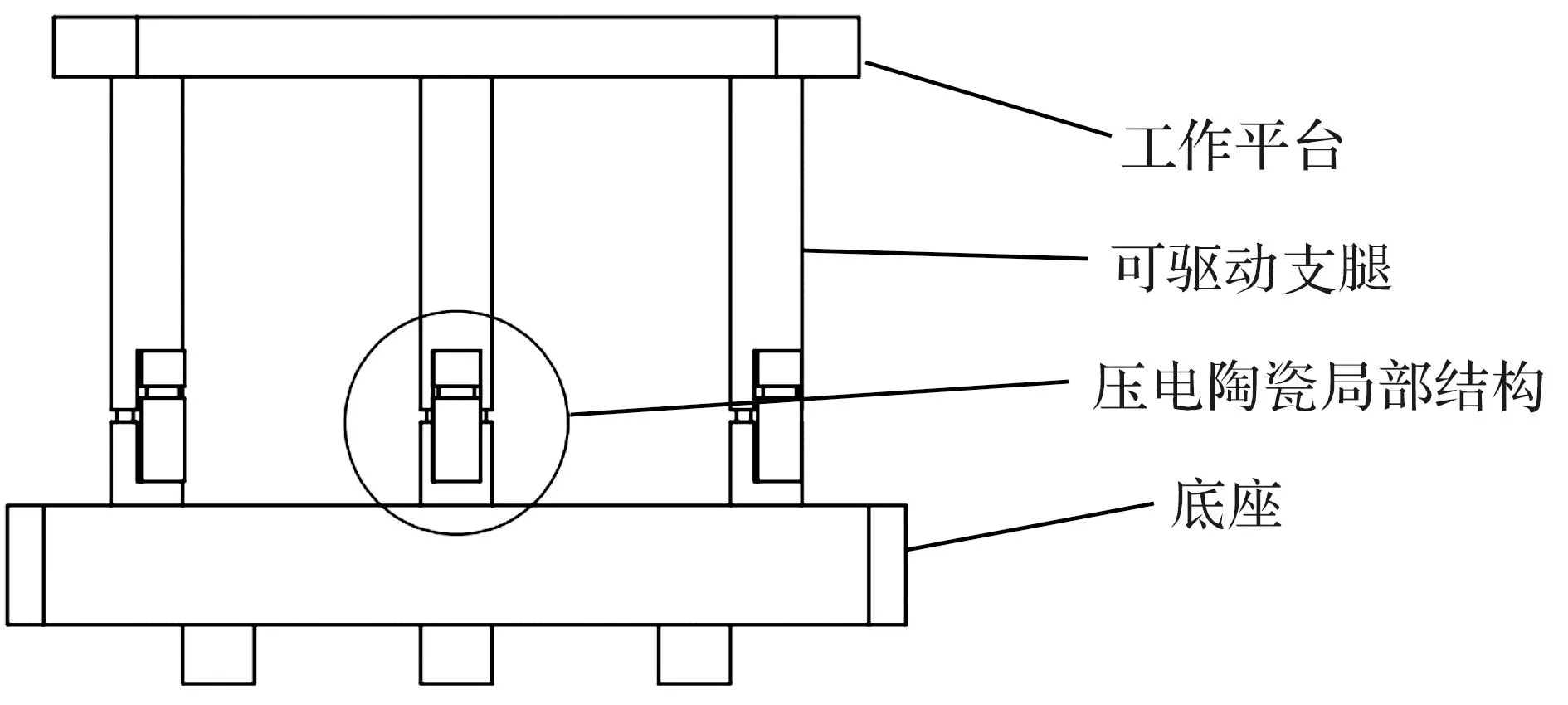
图1 调平机构整体结构主视图Fig.1 Front view of overall structure of leveling mechanism
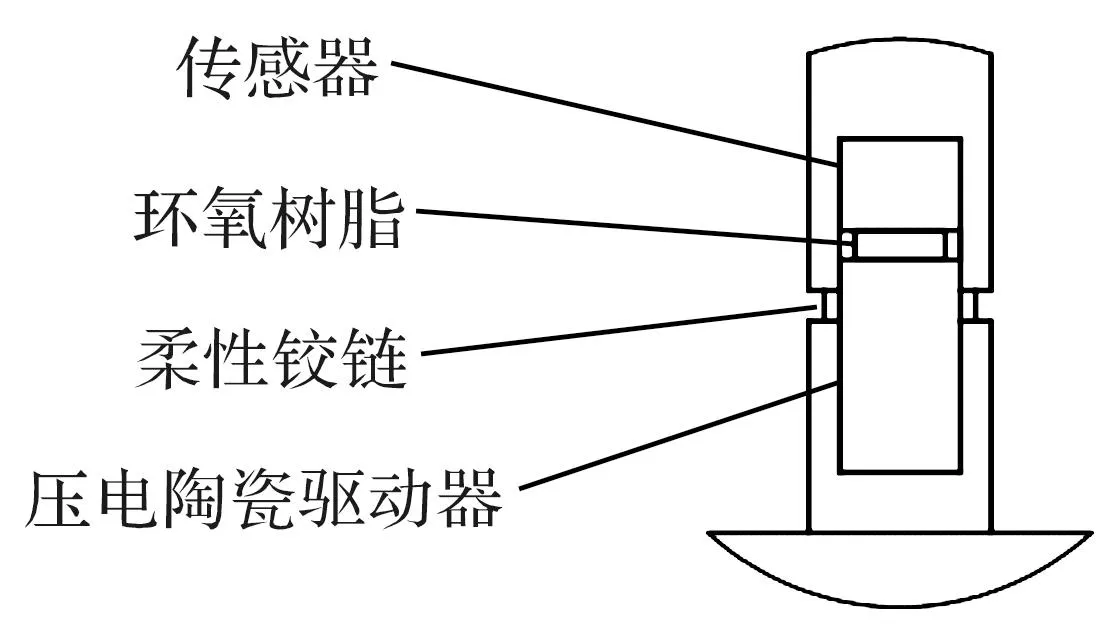
图2 压电陶瓷的局部结构Fig.2 Localized structure of piezoelectric ceramics
压电陶瓷的微小形变由施加到PZT功能材料上的电压大小来控制。调平顺序如下:工作载荷→支腿受力→比较各分力大小→施加驱动电压→PZT形变产生微动位移→分力差值在精度阈值内→调平结束。调平过程几乎没有能量损失,能够满足高精度的调平要求。
1.1 调平步骤
在工作平台施加载荷F,3只可驱动支腿的分力分别为F1、F2、F3,对应的压电陶瓷结构中压电陶瓷传感器所产生的电压值分别为U1、U2、U3。根据压电陶瓷在电场中的逆压电效应[12],压电陶瓷应变量表示如下:
(1)
式(1)中:ε为压电陶瓷驱动器的应变量;c为压电陶瓷材料的压电系数;M为压电陶瓷材料的电致伸缩系数;d为组成压电陶瓷驱动器与压电陶瓷传感器的单组极板之间的距离。
施加驱动电压后,压电陶瓷驱动器所产生的驱动力f1、f2、f3与驱动电压U1、U2、U3的关系式如下:
(2)
式(2)中:E为PZT的杨氏模量;A为可驱动支腿的横截面积。
调平机构的工作流程图见图3。

图3 工作流程图Fig.3 Work flow chart
当工作平台承受外部作用力F时,各驱动支腿受分力示意图见图4,图中a为等边三角形工作平台边长的1/2,(x,y)为工作平台作用力F作用点的坐标。
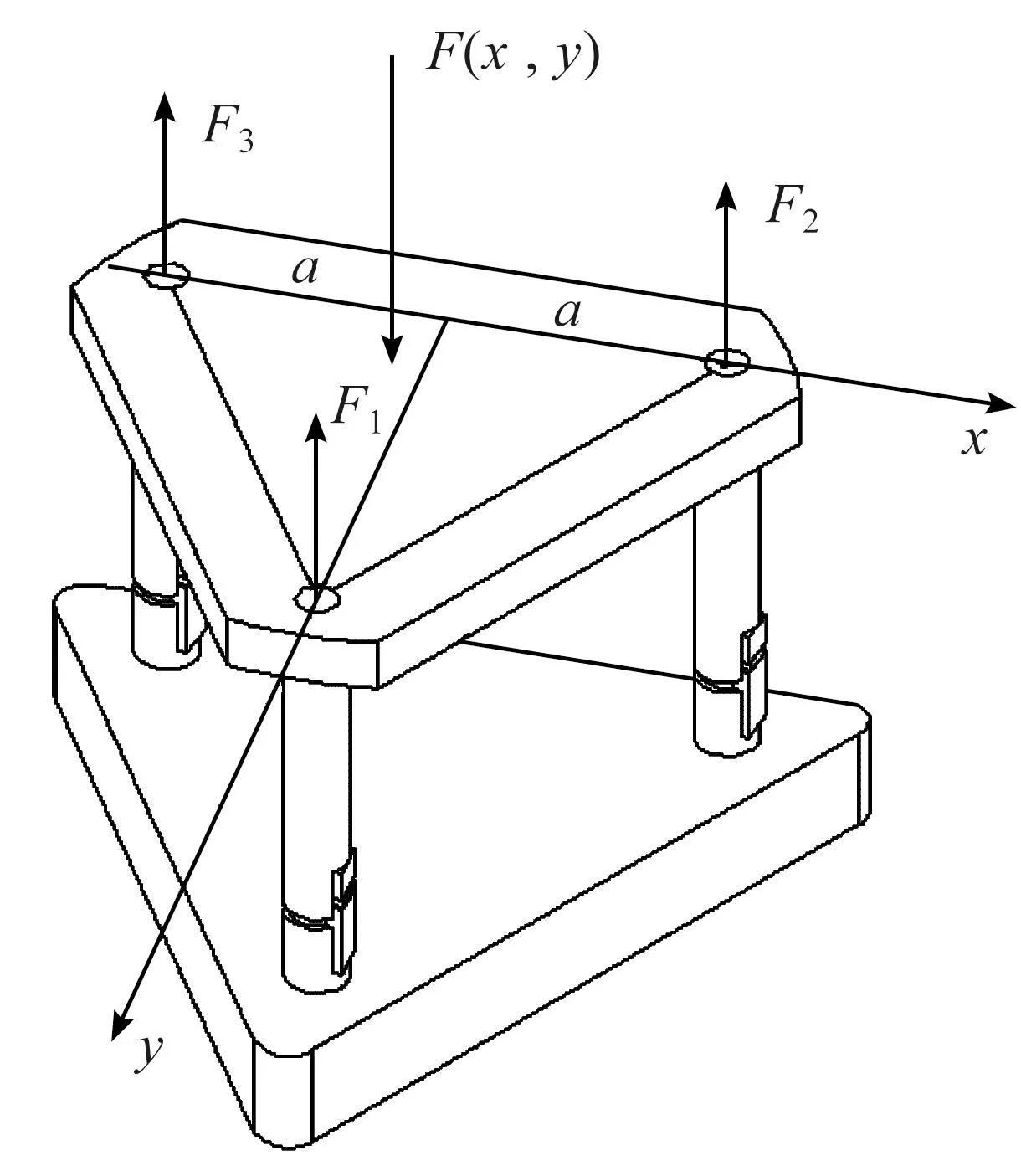
图4 各驱动支腿受分力示意图Fig.4 Schematic diagram of force component of each driving outrigger
根据空间平行力系可求得各支腿分力之间的关系式如下:
(3)
根据式(3)推导出F1、F2、F3后,3只可驱动支腿的受力情况可分为三力相等、三力互不相等,以及三力中有两力相等且小于第三力及三力中有两力相等且大于第三力4种情况。由于工作平台为等边三角形结构,为不失一般性,三力关系可表达为F1=F2=F3、F1
1) 当F1=F2=F3时,工作平台处于水平状态,无须调平。
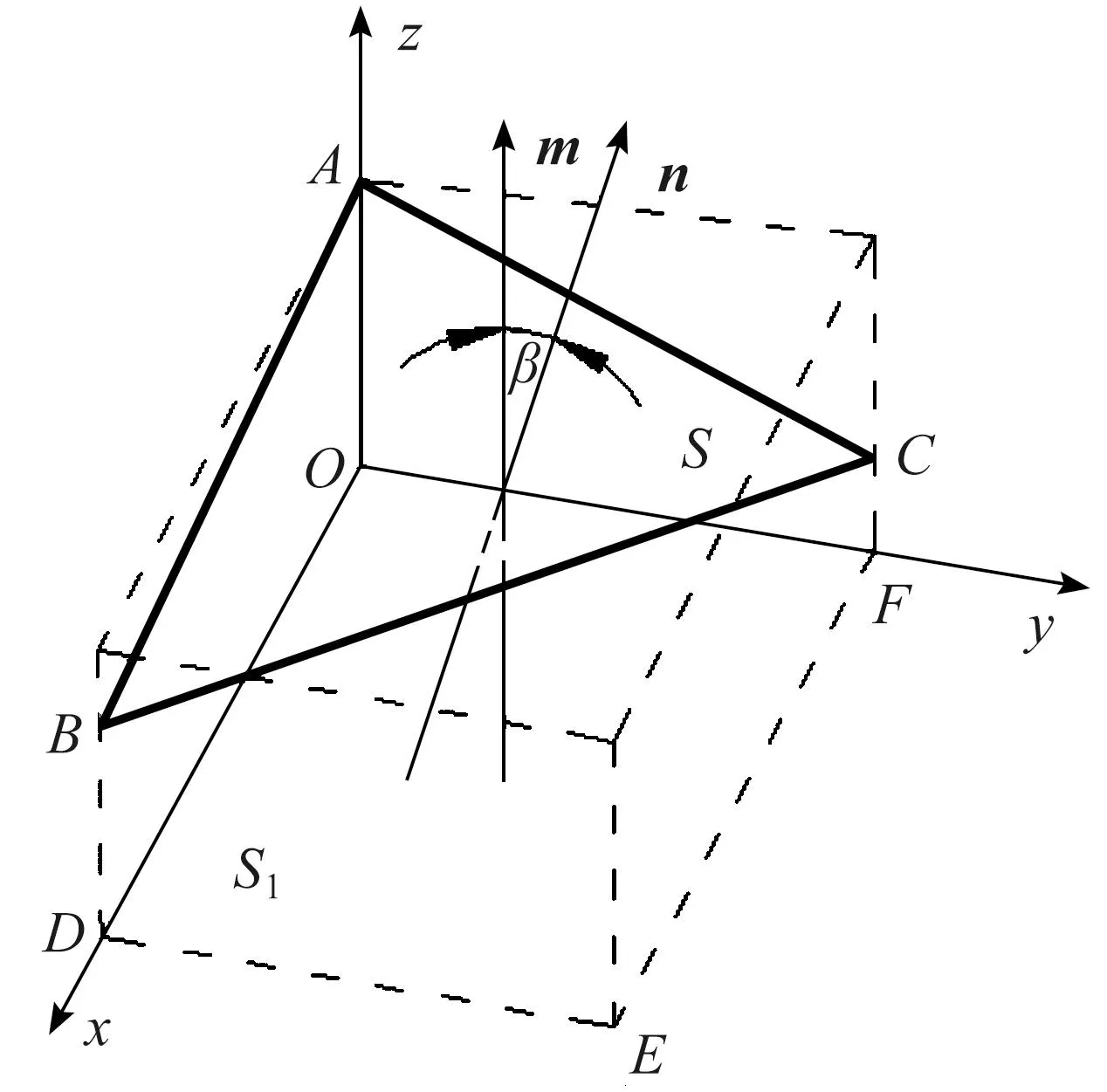
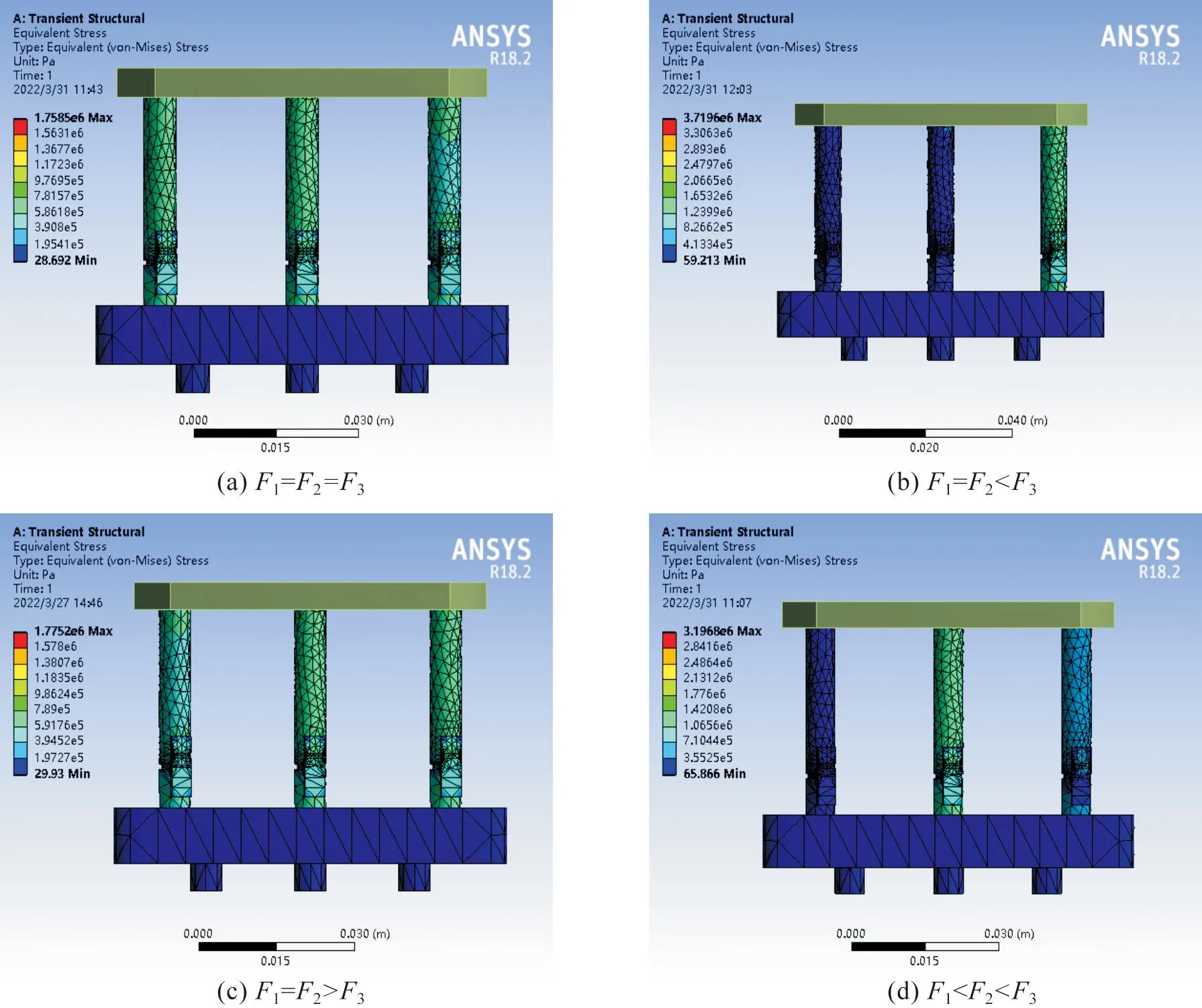
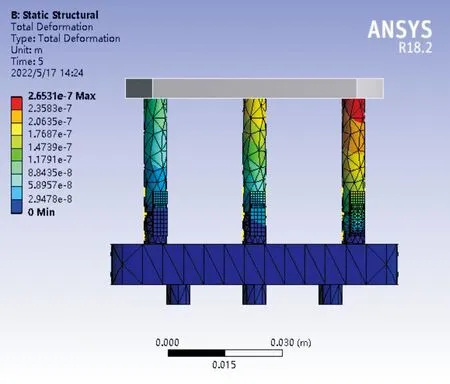
2) 当F1 (4) 式(4)中:ΔLi(i=1,2,3)分别为各可驱动支腿的形变量;Fi(i=1,2,3)分别对应第一、第二、第三可驱动支腿所分担的压力,L为可驱动支腿的长度。 初始状态下,可驱动支腿的长度相等。此时3只可驱动支腿的形变量之差分别如下: (5) 此时平台要恢复水平状态,应使第二压电驱动器的形变量等于ΔL2-ΔL1,第三压电驱动器的形变量等于ΔL3-ΔL1,即 (6) 式(6)中:Lp为压电陶瓷驱动器长度。 对第二可驱动支腿处的压电陶瓷驱动器施加驱动电压U′2,第三可驱动支腿处的压电陶瓷驱动器施加驱动电压U′3: (7) 检测第一可驱动支腿中由于第二可驱动支腿和第三可驱动支腿伸缩而产生的分力的增量ΔF1。其中ΔU1是在ΔF1作用下第一可驱动支腿上的压电陶瓷传感器所产生的电压;δ为精度阈值,根据工作平台所需要的工况调平精度确定;若ΔF1<δ,则调平结束。 (8) 否则第二和第三可驱动支腿处的压电陶瓷驱动器施加驱动电压修改为U″2、U″3: (9) 3) 当F1=F2 (10) 若ΔF′1<δ,则调平结束;否则重新对第三可驱动支腿处的压电陶瓷驱动器施加驱动电压U″3: U″3=U′3-ΔU1。 (11) 4) 当F1=F2>F3时,需同时对第一、第二两支腿施加相等电压U′1,得到第一、第二两支腿因此产生的分力增量。若ΔF′1>δ,则重新施加驱动电压U″1: (12) 调平步骤完成后需要进行水平度分析,本研究以倾斜角大小作为衡量工作平台水平度的标准[13-15];倾斜角即工作平台倾斜后的平面与基准平面所形成的夹角,在工作平台受外力产生倾斜后,通过推导倾斜角与支腿形变量之间的关系来分析工作平台的水平度,由此判断工作平台水平度是否满足工况精度要求。由于工作平台受力时可驱动支腿产生的4种受力情况而产生的受力形变情况见图5。 图5 各支腿受力形变情况Fig.5 Force and deformation of each outrigger 支腿受力形变情况为ΔL1≠ΔL2≠ΔL3时的倾斜角示意图见图6,图中A(0,0,z1)、B(x,0,z2)、C(0,y,z3)、D(x,0,0)、E(x,y,0)、F(0,y,0)。图6中由于各支腿受力形变均不相同,工作平台在立体空间内可向任何方向倾斜,故采用向量法分析倾斜角。设平台ABC受力时A点支腿受力最小,C点支腿受力最大,则支腿间的形变量为z1-z3=ΔL3-ΔL1,z1-z2=ΔL2-ΔL1,工作平台ABC的法向量为n,水平基准面S1法向量为m=(0,0,1),再将式(5)代入面S和面S1夹角β的余弦值cosβ,此时β为倾斜角,即 (13) 图6 倾斜角示意图Fig.6 Schematic diagram of tilt angle 图7 工作平台面与倾斜面的几何关系Fig.7 Geometric relationship between working platform surface and inclined surface 由图7可知,支腿形变量与工作平台倾斜角的数学关系为 (14) 由于β→0,故上式简化为 sinβ≈β。 当工作平台受力时,各支腿形变量如式(4)所示。将式(4)代入式(14)可得各支腿由于形变量而造成的倾斜角为 (15) 当工作平台受力产生倾角时,按上述调平步骤,将式(6)的支腿形变量之差代入式(14),可得调平的理论倾斜角 (16) 在调平步骤完成后,验证工作平台水平度时,将ΔF代入式(15),可得: (17) 又因ΔF<δ,将式(10)代入式(17),则倾斜角与精度阈值满足如下关系: 1.59×107β′=ΔF<δ。 对机构材料进行定义,压电片选择PZT-4压电材料,密度ρ为7 450 kg/m3,泊松比为0.269,杨氏模量E为1.06×1011(Pa)。工作平台结构选用碳素结构钢材料,密度ρ=7.85 g/cm3,弹性模量E的范围为200~210 GPa,泊松比的范围为0.25~0.33。沿竖直方向极化的材料刚度矩阵K(×1010N/m2)、压电矩阵d(C/m2)和介电矩阵ε分别如下: 在仿真软件前处理模块中,首先对调平机构进行网格化处理,网格化处理方式决定了仿真结果的精准度,主要包括材料属性定义、网格属性定义、网格划分等步骤。 驱动电压在压电求解时,PZT材料在竖直方向极化,耦合上下表面电压。压电片网格化共生成5 906个结点和1 190个单元,示意图见图8。压电驱动模块工作示意图见图9。 图8 压电片网格化示意图Fig.8 Schematic diagram of piezoelectric grid 图9 压电驱动模块示意图Fig.9 Schematic diagram of piezoelectric drive module 2.2.1 支腿受力分布仿真 在调平分析中,对支腿施加电压前必须了解各支腿的受力情况。分析支腿受力情况时,定义工作平台模拟载荷F为50 N。当外载荷作用点发生变化时,支腿受力状况也将发生变化,故将受力点分别设置在工作平台中心点、中心线等不同区域。各可驱动支腿形变及受力的4种情况如图10所示。 图10 各可驱动支腿形变及受力的4种情况Fig.10 Four conditions of deformation and force of each drivable outrigger 由图10(a)可知,当受力点在中心点时,各支腿受力相等,即F1=F2=F3;由图10(b)、(c)可知,当受力点在中心线上分布时,其中两个支腿受力相等;图10(d)表示当受力点位于其他区域时,各支腿受力均不相等,用F1 图11 工作平台的受力区域与各支腿的受力分布关系Fig.11 Force distribution relationship between force bearing area of working platform and each outrigger 2.2.2 支腿受力形变仿真 为便于计算所需要的微动位移补偿,因此要分析支腿因受力而产生的形变情况。通过仿真得到各支腿的形变量后,再对压电陶瓷驱动器施加驱动电压使其产生等量级的位移补偿。4种受力情况下支腿受力产生的形变如图12所示,由图可知,当受力点位于工作平台的不同区域时,各支腿的形变量与其所受分力大小呈正相关变化。 图12 4种受力情况下支腿受力产生的形变Fig.12 Deformation of outrigger under four force conditions 由图12(a)可知,各支腿形变量相等,即ΔL1=ΔL2=ΔL3;图12(b)、(c)表示形变量为ΔL1=ΔL2<ΔL3和ΔL1=ΔL2>ΔL3的2种情况,其中两支腿形变量ΔL1、ΔL2分别为-3.07×10-8~-9.22×10-8(m)和-1.42×10-8~-1.27×10-7(m),ΔL3为-3.07×10-8~-2.77×10-7(m)和-1.42×10-8~-1.13×10-7(m);图12(d)表示各支腿形变量的关系为ΔL1≠ΔL2≠ΔL3,其中各支腿的形变范围分别为-2.89×10-8~-8.68×10-8(m)、-2.89×10-8~-1.16×10-7(m)、-2.89×10-8~-2.60×10-7(m)。 以F1=F2 驱动电压在10~150 V范围内时,代入式(2)、式(6)中得到的压电陶瓷理论受力与变形关系曲线如图13所示。由驱动力曲线可知,对压电陶瓷驱动器施加驱动电压后产生的驱动力f在0~13 N范围内,与工作平台支腿所受分力大小F在同一量级范围内;由压电陶瓷形变曲线可知,施加电压产生的位移范围在10-8~10-7m。与上述受力形变的仿真结果相比,验证了支腿受力时的形变量与压电陶瓷产生的微动位移量的统一。从理论计算来看,结合式(19)、式(20),调平前后工作平台倾斜角变化曲线如图14所示。平台受外力时产生的倾斜角为β,调平后的倾斜角为β′。以支腿横截面受分力的大小为0~13 N范围内为例,工作平台在受外力时产生的最大倾斜角为2.15×10-6(°),施加驱动电压后倾斜角减少了1.95×10-6(°)。理论计算可得调平后工作平台倾斜角可减小到原来的10%。 图13 压电陶瓷驱动电压理论受力与形变关系曲线Fig.13 Relation curve between theoretical force and deformation of piezoelectric ceramic driving voltage 图14 调平前后工作平台倾斜角变化曲线Fig.14 Change curve of tilt angle of working platform before and after leveling 在ANSYS压电耦合仿真分析中,根据具体工况对压电模块进行建模,压电陶瓷驱动器长度为7 mm,驱动电压范围为10~150 V。当应力作用在可驱动支腿横截面上时,在竖直方向产生压缩变形。而在压电陶瓷两端施加电压后,对可驱动支腿的竖直方向产生相应的微动位移。当外力50 N作用在平台中心线时,取压电陶瓷处的仿真应力值为6×105(Pa),支腿横截面积S=25.13×10-6(m2),通过上述工作原理计算,得出1只腿分力F为15.078 N,代入式(2)可得该支腿压电陶瓷驱动器在上述工况下的驱动电源电压理论值约为43 V,理论形变量为-1.038×10-7(m)。 电压值为43 V的压电陶瓷微动位移仿真结果如图15所示,由图可知,支腿的微动位移仿真值基本上在1.072×10-7~1.787×10-7(m)之间。与图12(a)、(b)和(c)的支腿形变量仿真结果相比,压电陶瓷微动位移仿真结果与受支腿分力时的理论形变量在同一量级范围内,理论形变量ΔL=-1.038×10-7(m),与仿真结果的误差值为0.034×10-7(m),误差波动为3.276%,在合理范围内。 图15 压电陶瓷微动位移仿真结果Fig.15 Simulation results of piezoelectric after ceramic fretting displacement 根据图12(b)仿真结果进行计算,当工作平台受外力作用时支腿所受分力差值ΔF的形变阈值ΔL=4.65×10-8(m)。对形变量最大的支腿压电陶瓷驱动器施加驱动电压后,各支腿因受力差而产生的形变情况如图16所示,理论计算可得ΔL′=-2.94×10-8(mm)。将ΔL、ΔL′分别代入式(19)可得:调平前倾斜角为1.12×10-6(°),调平后倾斜角β″减小了0.71×10-6(°)。仿真结果可得调平后工作平台倾斜角可减小到原来的37%。 图16 施加电压后各支腿因受力差产生的形变Fig.16 Deformation of each outrigger due to force difference applying voltage 基于压电陶瓷功能材料在机械工程领域的应用,提出了一种基于压电材料逆压电特性的调平方法。首先推导出力的作用点与各支腿分力之间的相互关系;再利用ANSYS中的瞬态结构模块进行仿真试验,结果表明调平理论计算值与仿真试验值处于同一量级范围,可实现微米级精度的水平调节功能。通过平台平面度验证,当支腿分力产生的增量在精度阈值范围内时,则符合调平要求。相比四支点支撑结构,本研究提出的等边三支腿结构具有稳定性好、支撑可靠性高等优点,避免了因“虚腿”而造成支腿受力不均的现象,其应用场合更加广泛,具有控制逻辑清晰、响应速度快、调整精度高等特点。1.2 工作平台倾斜角分析

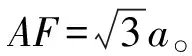
2 ANSYS模拟仿真
2.1 仿真前处理
2.2 加载与求解

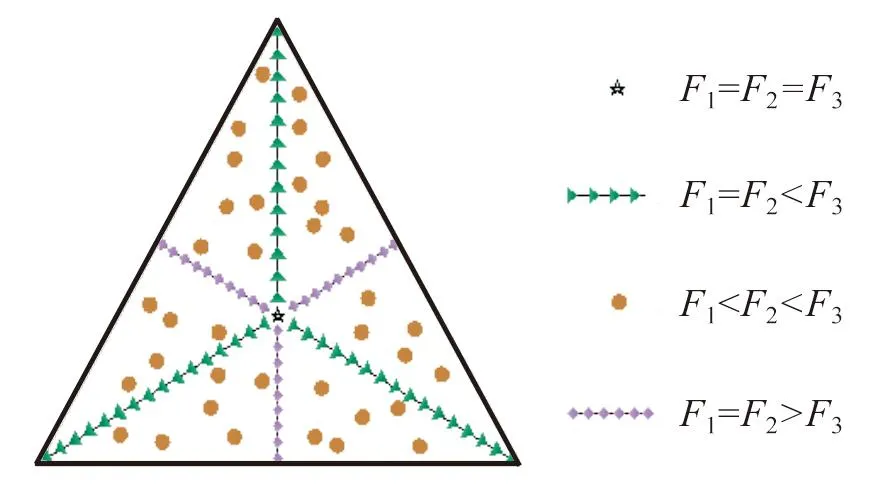
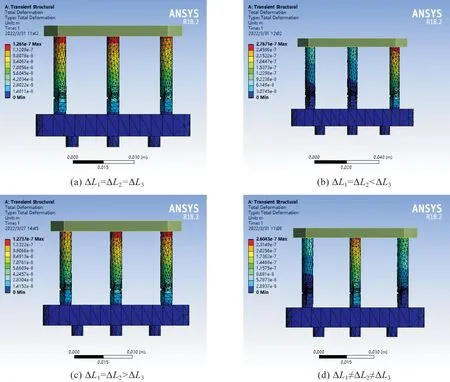
3 调平结果分析
3.1 倾斜角理论分析
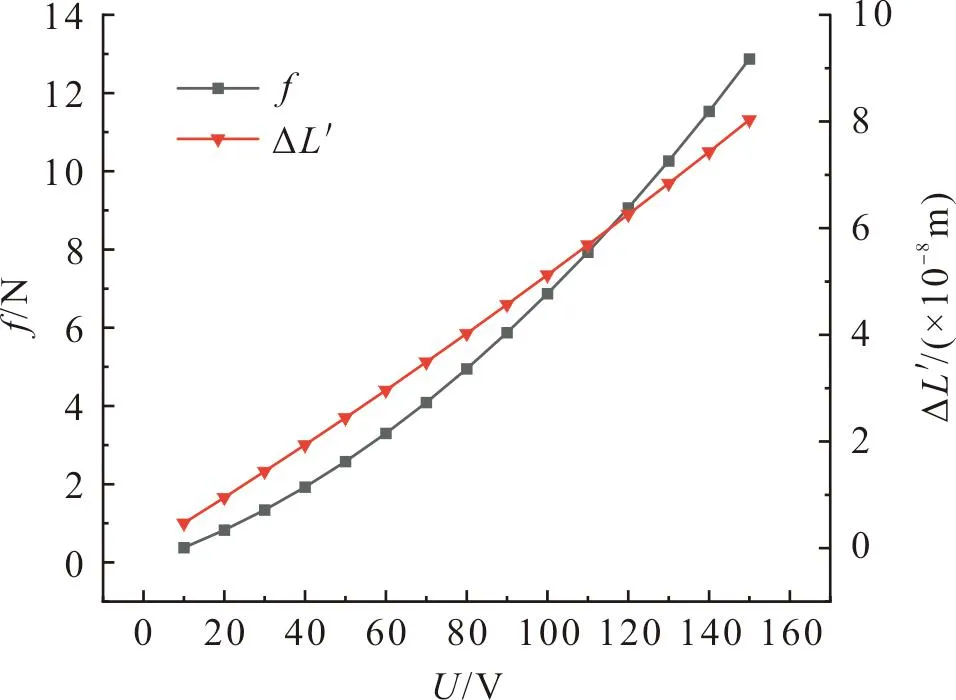
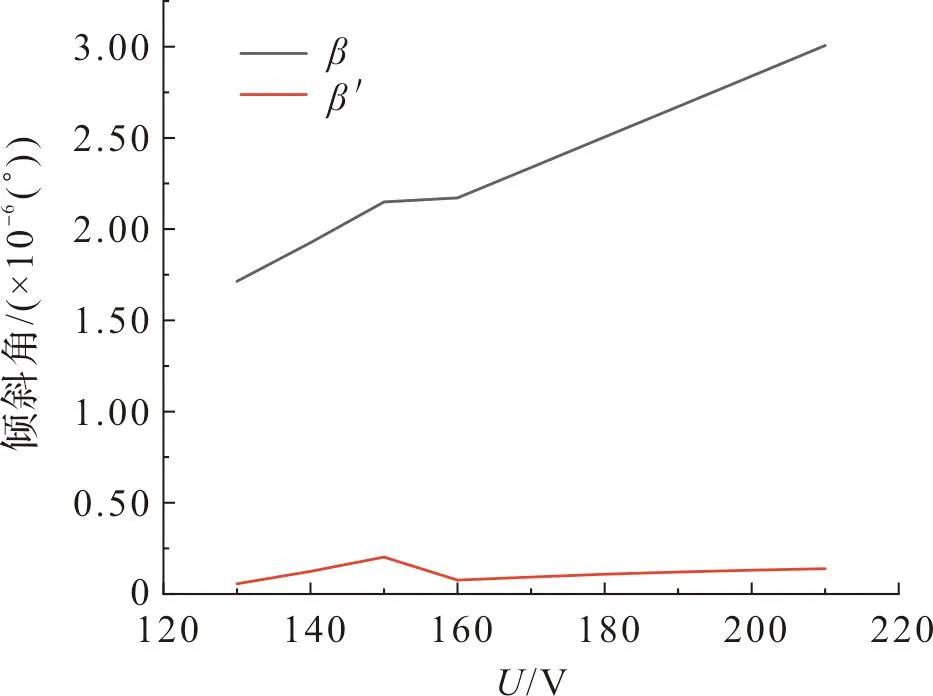
3.2 倾斜角仿真分析

4 结 语
