波浪荷载作用下群桩筒基础动力响应研究

左 熹，许 想，周恩全

(1.金陵科技学院建筑工程学院，江苏 南京 211169；2. 江苏大学土木工程与力学学院，江苏 镇江 212005)

0 引 言

海上风电基础需要足够的承载力以维系风机正常运行时的安全和稳定性能。单桩基础的应用十分广泛，但缺点是侧向刚度不足，会产生难以进行控制的水平变位现象[1]；筒型基础的发展前景非常广阔，但在承载力不足的条件下往往易发生沉陷、平移或者倾倒的现象[2]。本文提出在现有的筒型基础内部增加钢管桩，形成新型海上风电群桩筒型基础，增大了基础整体与地基土体之间的接触面积，提升了基础与地基土之间的协同度，有效地提高了群桩筒基础的承载能力。

海上风机所处海洋环境复杂，在正常运行的过程中会受到各种动、静荷载的长期作用，由此会对其结构寿命产生一定的影响，因此研究周期性波浪荷载作用下基础的动力响应对结构长期稳定的运行具有十分重要的意义。目前对于波浪荷载的作用研究，大多以理论分析以及数值模拟为主。于聪[3]借助于流体力学软件Open FOAM和有限元软件ABAQUS，建立复合筒型基础的集成模型，研究了其在波浪荷载下的动力响应；戴澍[4]等依据莫里森方程式编写相关的FORTRAN代码，将波浪的作用效果等效成分布荷载作用的形式施加到各单元，并结合ABAQUS中的子程序功能进行波浪力的相关计算。Chang等[5]基于斯托克(Stokes)方程及Biot理论，通过COMSOL软件，综合三维波浪和海床模型，建立了三维多孔模型，模拟东海海域风电机基础的波浪-海床-结构间的相互作用。Lin等[6]基于FLUENT软件，开发了一个可以模拟非线性波浪作用下不同风机基础中波浪爬高和波浪载荷的计算流体动力学模型，可见数值模拟是进行波浪荷载的强有力的分析方法之一。在进行浪荷载下群桩筒基础动力响应研究前，需要理解波浪理论的概念，并选择合适的波浪理论，进行波浪荷载的计算。

本文根据小尺寸构件的波浪力的计算方法，结合莫里森方程得到波浪荷载的时程曲线，将具有周期性变化的波浪荷载施加在群桩筒基础上，从而研究群桩筒基础在波浪荷载作用下的动力响应。

1 群桩筒基础结构

海上风电群桩筒基础的构造形式是在传统的筒型基础内部安装数量不等的钢管桩，钢管桩与筒顶盖连接，筒型基础为已有的大直径宽浅式基础。基础整体采用钢材制作，上部连接直线形过渡段，如图1所示。

图1 桩筒复合基础示意

2 波浪运动理论

2.1 莫里森方程

构件的横向尺寸与波长的比值较小(D/L<0.15)的海洋工程建筑物，可以忽略结构对波浪运动带来的影响，此时，对于小尺寸建筑物，波浪作用主要是粘滞效应、附加质量效应。其波浪力的计算方式，一般选用莫里森(1950年)提出的计算方法。波浪在经过小尺寸构件时，形成了绕流，此时无绕射反应发生，即小尺寸构件的存在并没有影响波浪的原有状态。

莫里森(1950年)认为桩体上高度为z处受到的水平波浪力由两部分分量组成[7]：

(1)由波浪中的水质点因自身水平速度vx引起的对桩的速度力，即水平拖曳力。对处于理想状态的流体，一般忽略其黏性产生的影响，且作平稳势流运动。当波浪经过桩时，桩身位置前后及上下的对称点所受压力处于平衡，桩上所受波浪力达到平衡，即理想流体中的桩不受波浪力。实际条件中海域中海水是存在粘滞性的，即流体与桩表面形成的边界层会引起较大值的摩擦切应力。此时，边界层处流体与桩出现分离，使桩后部压强值小于桩前，桩前后压力出现差值，从而导致流动方向上的波浪力的产生。单位桩长的最大速度力为

(1)

(2)波浪水质点产生的加速度会带来惯性力的作用。假定流体为理想状态，具有不可压缩的特性，波浪运动过程中，因为柱体的存在，使得流场中水的速度发生变化，由此引起了流体出现对柱的沿流体运动方向的惯性力。单位桩长的最大惯性力为

(2)

式中，Cd为惯性力系数。其他符号含义同前。

对于小尺度构件(D/L<0.15)的波浪力，其存在对波浪的运动不会产生影响，则所受波浪力为

f=fxi+fxd=-fximaxsinwt+fxdmaxcoswt|coswt|

(3)

其中，fximax、fxdmax由式(1)、(2)得出，ω为波浪的运动频率。

2.2 海流力

莫里森计算方法中，仅考虑波浪的单独作用结果，忽略了波浪与海流的相互作用。在实际的海洋环境中，相互作用的情况时常发生，因此，在计算波浪荷载作用的时候，需要考虑海流带来的影响。

与具有周期性运动规律的波浪运动相比，海流在速度上变化趋势较慢，通常假定为常水流，且仅对构件存在拖曳力。在竖直方向，假定海流速度相等，即竖直方向的拖曳力也相等。海流会影响波浪原有的运动形式，当两者的运动方向一致时，海流会减缓波形并降低波浪高度，反之则增大波高，使波形陡峭。

当海流与波浪运方向存在夹角φ的情况下，波流联合作用下的拖拽力为

(4)

分量表达式为

(5)

(6)

式中，FD为拖拽力；CD为拖曳力系数；ρ为海水密度；D为桩径；v和vc分别为波浪及海流的速度矢量；FDx和FDy为拖拽力分量；vx为波浪质点的速度；φ为拖拽力分量夹角。

波浪力计算公式为

(7)

(8)

式中，Fx和Fy为波浪力分量；Cd为波浪力系数；ρ为海水密度；D为桩径；v和vc分别为波浪及海流的速度矢量；CM为惯性力系数；vx为波浪质点的速度；φ为波浪分量夹角。

当海流与波浪运动方向一致时，波流联合作用下的拖拽力为

(9)

3 波浪荷载作用下群桩筒基础动力响应

本文以江苏灌云某地近海的5 MW风电机为研究对象，结合其所处位置的海洋环境参数(海水密度1 030 kg/m3，波长74.1 m；有效波高2.8 m)及群桩筒基础的结构尺寸(D/L=6/74.1=0.081<0.15)，根据莫里森方程中计算小尺寸构件波浪力的计算方法，按照式(1)、(2)、(3)计算波浪荷载的大小，取t=100 s时间内的波浪力变化的时程曲线如图2所示。

图2 海面波浪荷载时程曲线

波浪荷载的作用主体是基础结构，研究利用ABAQUS软件建立的三维群桩筒形基础模型，将具有周期性变化的波浪荷载施加在基础顶部一点[8]，如图3所示，进而研究群桩筒基础在波浪荷载作用下的动力响应。建立了单筒(B0P基础)、单筒加1桩(B1P基础)、单筒加3桩(B3P基础)和单筒加4桩(B4P基础)的4种基础形式的三维有限元模型。

图3 波浪加载示意

群桩筒基础中筒型基础和钢管桩都由钢材构成，材料密度7 850 kg/m3，杨氏模量2.1×105MPa，屈服强度345 MPa，泊松比0.3。建立的土体模型尺寸为：直径80 m，高60 m的圆柱形土体，能够避免土体的有限边界对计算结果精度的带来的影响，地基土体选用Mohr-Coulomb模型为土体本构模型，土层密度1 930 kg/m3，弹性模量12.1 MPa，泊松比0.33，摩擦角25.7°。模型尺寸参数见表1。

表1 基础形式及参数

3.1 应力分析

图4为水平波浪力作用下群桩筒基础顶盖中心点A位置处沿X轴方向的应力时程曲线。从图4可以看出，B4P基础在顶盖的峰值应力最大，其次是B0P、B3P基础，顶盖峰值应力最小的是B1P基础。根据有限元软件ABAQUS的计算结果可知，B4P基础在顶盖处的峰值应力值为30.29 kPa，而群桩筒基础结构使用的钢材为Q345，满足材料强度的要求。

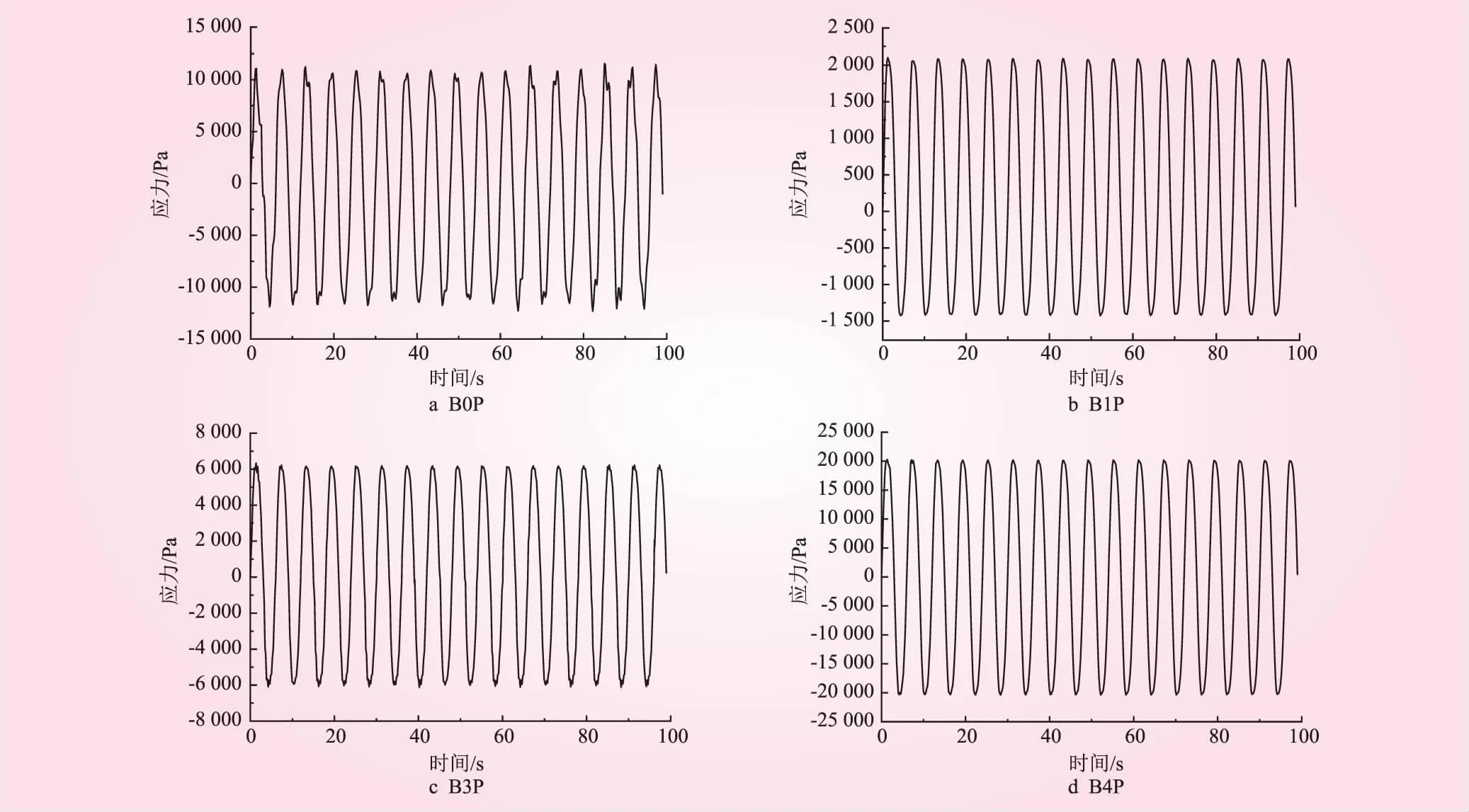
图4 群桩筒基础筒顶盖应力时程曲线

图5为B0P、B1P、B3P、B4P基础的应力分布云图。从图5可以看出：不同类型的基础中的应力集中区域均出现在顶盖位置，主要集中在上部过渡段与顶盖连接区域、桩与顶盖连接区域，表明顶盖部分是主要承担荷载区域，应对应力集中区域重点考虑。由B0P基础的应力云图可以看出，波浪力由过渡段传递到顶盖，再经顶盖传递到筒壁。而B1P、B3P、B4P基础与B0P基础相比，波浪力在由顶盖向下传递的时候，筒内钢管桩分担了较大一部分荷载，筒壁相对而言分担了较少的荷载，此时主要由筒内的钢管桩提供承载能力，筒壁发挥的效果不明显，随着荷载增大，筒壁逐渐发挥效用，即筒内桩的存在显著提升了基础的承载能力。

图5 群桩筒基础应力云图

图6为波浪荷载下，4种基础沿路径S1-S2方向筒壁应力分布规律。从图6可以看出，在波浪荷载作用下，B1P基础表现出的应力值较小，变化趋势比较稳定，B3P、B4P基础中应力的变化趋势相近，变化幅度较大，B0P的变化趋势介于B1P与B3P、B4P之间。总的来说，B1P在波浪荷载作用下表现的性能最好。

图6 筒壁沿深度的应力分布曲线

图7为群桩筒基础顶盖的应力云图。从图7可以看出，B1P基础顶盖的峰值应力最小，其次是B3P、B0P、B4P基础。B0P基础的顶盖应力分布较为均匀，4种基础的高应力分布区域均出现在过渡段与顶盖、桩与顶盖的连接处，即这些连接区域形成了应力集中区。

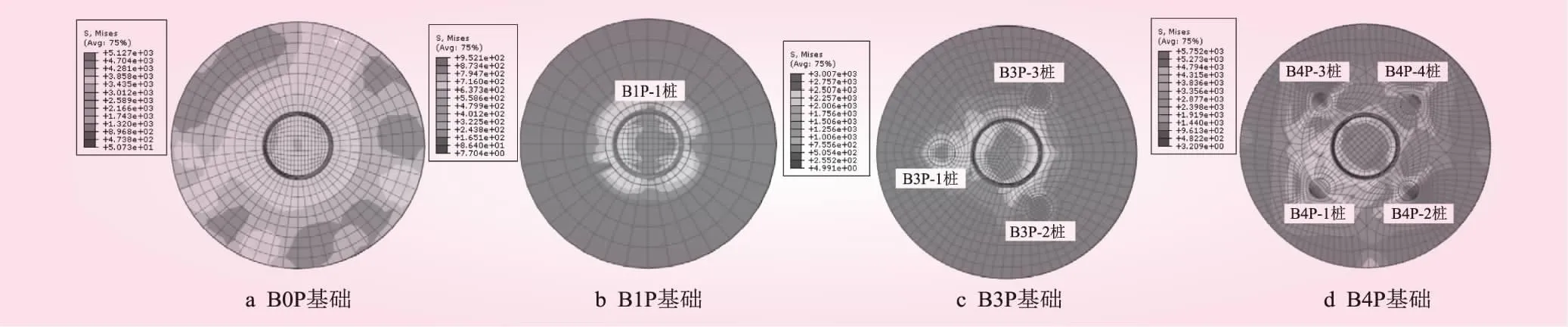
图7 群桩筒基础顶盖处应力云图

图8为B1P、B3P、B4P基础筒内桩身的应力云图。从图8可以看出，桩身可以有效分担上部传递荷载，桩身的高应力集中区域均出现在桩顶，即桩与顶盖连接区域，且应力值沿桩身向下方向逐渐减小，B1P基础内的桩身应力峰值最小，其次是B3P基础、B4P基础。

图8 群桩筒基础内部桩身应力云图

3.2 位移分析

图9为B0P、B1P、B3P、B4P基础顶部B点在X方向的位移时程曲线。从图9可以看出，在波浪作用下，B1P基础顶部的位移峰值最小，值为0.05 mm，紧接着是B3P、B4P、B0P基础，位移峰值分别为0.082、0.116、0.13 mm；变化趋势同波浪力一样，呈周期性变化。结合群桩筒基础顶部的位移峰值数据可以得到，在用钢量一定的条件下，群桩筒型基础比单一的筒型基础具有更好的抵抗波浪力冲击的效果，有限元结果表现为：B1P基础在波浪荷载作用下的稳定性能优于B3P、B4P、B0P基础。

图9 群桩筒基础顶部位移时程曲线

图10为B0P、B1P、B3P、B4P基础在提取路径为S1点处泥面沿X方向的位移时程曲线。根据计算结果中基础泥面的峰值位移数据可得，在波浪作用下，B1P基础泥面的位移峰值最小，为0.005 02 mm，其次是B3P、B4P、B0P基础，位移峰值分别为0.008 04、0.009 06、0.017 mm，表明在波浪荷载作用下，B1P基础具有更高的稳定性能，并优于B3P、B4P、B0P基础。

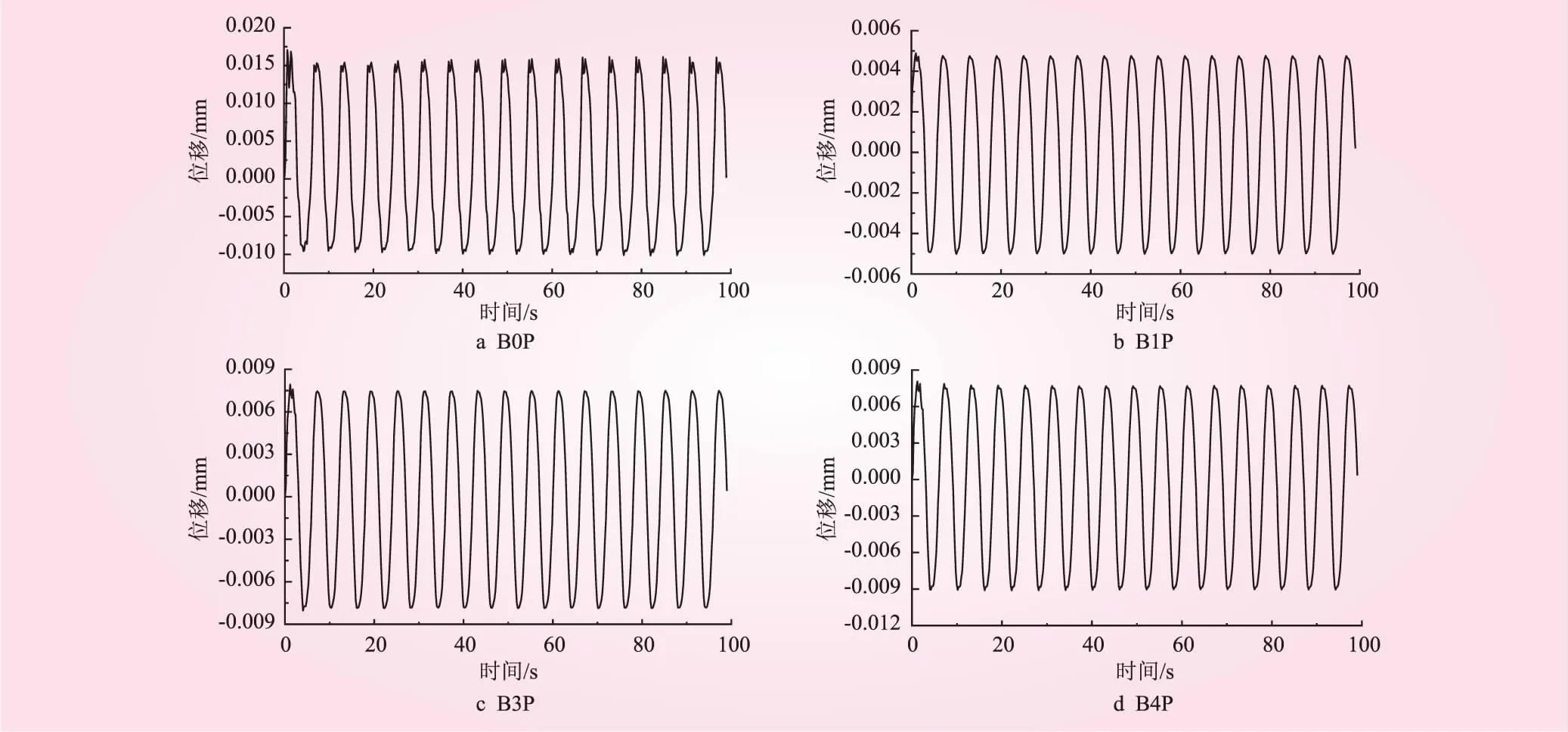
图10 群桩筒基础泥面位移时程曲线

综合比较B0P、B1P、B3P、B4P基础在波浪荷载下的动力响应结果明显可以看出，群桩筒基础的比单一的筒型基础具有更好的抵抗波浪荷载的能力，且B1P的抵抗波浪荷载的性能最优，其次是B3P基础、B4P基础、B0P基础。

4 结 论

基于波浪运动的基本概念，对现有的波浪理论和计算方法进行了总结，分析了波浪荷载计算方法的适用性。根据实际海洋环境的相关波浪参数，基于莫里森方程中小尺寸构件的波浪力的计算方法得到了波浪力关于时间的曲线，将具有周期性变化的波浪荷载施加在群桩筒基础模型顶部一点，研究群桩筒基础在波浪荷载作用下的动力响应，结论如下：

(1)波浪荷载作用下，基础的应力集中区域出现在顶盖与过渡段、顶盖与钢管桩连接区域，钢管桩桩身应力值大小沿深度向下递减。钢管桩对荷载的传递起到了很好的分担效果，有效地分担了筒壁承载的压力。

(2)通过对比波浪荷载作用下基础顶部和基础泥面的位移峰值大小得出，群桩筒基础比单一的筒型基础具有更好的抵抗波浪荷载的能力，即筒内桩基可以有效分担上部荷载，在用钢量相同时，B1P的抵抗波浪荷载的性能最优，其次是B3P基础、B4P基础、B0P基础。