不同深宽比矩形平面超高层建筑横风向风荷载的试验研究*
2023-12-27陈伟兴石碧青谢壮宁
陈伟兴, 吴 洁, 石碧青, 谢壮宁
(1 华南理工大学亚热带建筑与城市科学全国重点实验室,广州 510641;2 保利湾区投资发展有限公司,东莞 523123;3 奥雅纳工程咨询(上海)有限公司,上海 200031)
0 引言
随着我国经济的发展、建筑功能需求和土地价格的增长,矩形平面的扁长板式超高层住宅建筑不断衍生而出,在经济发达地区的高度已逼近200m。但是由于板式住宅结构主次轴刚度差异大,对风荷载的敏感性不同。文献[1]指出,200m左右或以上高度超高层建筑的横风向风荷载及其响应往往超过顺风向,成为板式住宅结构的控制荷载;另一方面,板式住宅结构的截面设计早已突破我国《建筑结构荷载规范》(GB 50009—2012)[2](简称荷载规范)中0.5~2的深宽比范围,在结构抗风设计中发现,若继续沿用相关标准规范方法计算横风向风荷载将会得到过于保守的结果。
目前针对超高层建筑顺风向风荷载的研究工作已趋于成熟,等效静力风荷载的概念及各类风致响应计算方法[3-5]被诸多学者提出,而针对复杂的横风向风效应问题,国内外风工程研究人员进行了大量的研究工作:全涌等[6]在4种不同地貌中对15种不同外形的超高层建筑的刚性模型进行了风洞试验,拟合出一个以地貌类型、模型长细比和宽厚比为参数的超高层建筑横风向广义气动力谱的闭合表达式;梁枢果等[7]针对四种矩形截面的高层建筑进行了风洞试验,研究表明:当1/4≤D/B(深宽比)<3时,横风力功率谱密度曲线只有一个谱峰,由旋涡脱落引起,当3≤D/B≤4时,横风力功率谱密度曲线有两个谱峰,分别由初级旋涡和分离流再附引起的次级旋涡脱落产生;唐意等[8]总结了矩形截面高层建筑横风向脉动风力的基本特征,拟合得到了以地貌类型和厚宽比为基本变量的超高层建筑横风向脉动风力根方差系数、竖向相关系数及功率谱密度的闭合计算公式;全涌、顾明等[9]对一高宽比为10左右的高层建筑刚性模型进行了风洞试验,发现此类建筑基阶固有频率接近尾流旋涡脱落频率并且诱发结构发生强烈的横风向共振,增大截面边长或增大结构刚度能有效降低高层建筑的横风向等效风荷载。
以上研究工作成果奠定了荷载规范中横风向条文的基础,荷载规范中提供的横风向等效静力风荷载计算公式分别考虑了地面粗糙度、矩形截面厚宽比以及常见削角或凹角的修正,应用范围和适应性和国外规范相比有很大的拓展。
已有研究主要存在的问题是:1)荷载规范没有充分考虑到D/B>2的情况,工程实践中常常发现大深宽比建筑按荷载规范计算得到的横风向风荷载明显高于风洞试验值;2)流场湍流度是影响超高层建筑横风向风荷载的一个关键指标,到2012年,我国荷载规范才明确定义了不同地貌类型的湍流度分布[10]且其值均不同程度地高于早期版本的隐含值;3)由于缺乏标准导致早期风洞试验风场模拟的结果相对过于离散,从而会导致风洞试验的离散性。
针对以上问题,本文采用高频底座测力天平技术,在B、C两类地貌中对28个超高层建筑模型进行了详细的风洞试验,本文主要介绍其中7种深宽比矩形平面超高层建筑模型的试验结果,分析了深宽比、湍流度、结构周期和阻尼比对横风向风荷载的影响规律,并与荷载规范结果比较。
1 风洞试验概况
1.1 试验风场模拟
风洞试验段长24m、宽5.4m、高3m,试验段后端配置4m直径转盘,试验风速在0~30m/s范围连续可调,测力试验采用高频底座测力天平(HFFB),通过安装在模型底部的高灵敏度天平测得结构在风荷载作用下的各基底力及倾覆力矩。
试验在B、C两类地貌下进行,试验风场根据荷载规范相关规定实施模拟,图1为本文试验的B、C两类地貌的平均风速剖面和湍流强度分布。
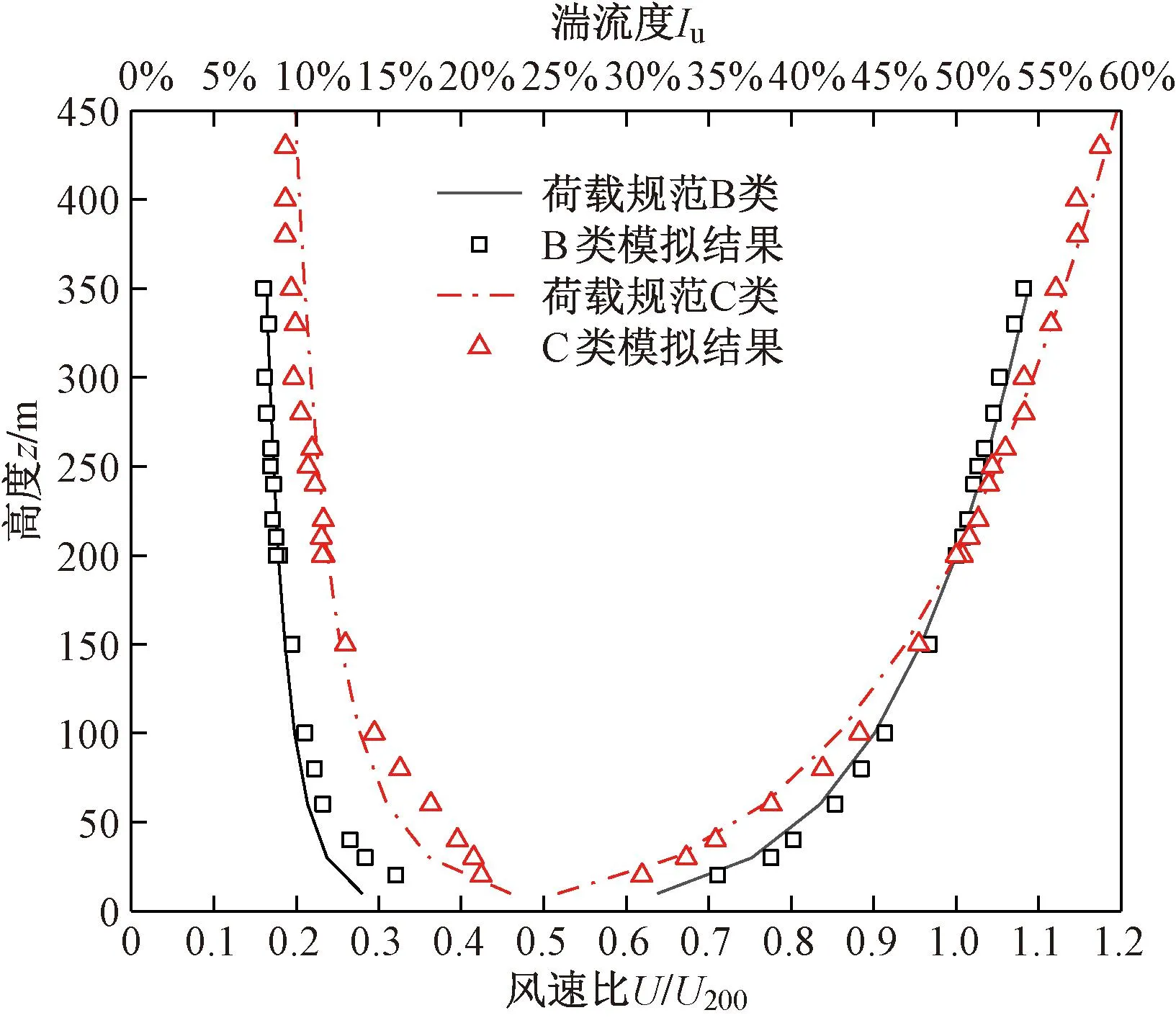
图1 B、C类地貌的平均风速剖面和湍流强度分布
1.2 试验模型及工况
为提高试验效率和模型精度,试验模型采用3D打印方式制作。通过预留的凹槽和扣件的相互拼接可以实现不同工况下的模型组合,这种组合方式可在一定程度上满足试验模型轻质高强的要求,试验模型如图2所示。

图2 试验模型照片
试验几何缩尺比为1∶400,建筑原型顶部高度均为200m,对应风洞中模型顶部高度为0.5m,高宽比为10,试验采样频率为 400Hz,样本帧数为 40 960,采样时间为102.4s,试验风场共B、C两类地貌,每类地貌下共进行1∶1、1.5∶1、2∶1、2.5∶1、3∶1、4∶1、5∶1深宽比工况的模型试验。图3给出了试验风向角和顺、横风向基底气动弯矩响应的方向定义,以正东方向为 0°风向角,以逆时针方向进行 0°、15°、30°、45°、60°、75°、90°、180°、270°、345°等10个风向角的测试。顺、横风向的基底气动弯矩仅是针对某一风向角定义,当风向角为0°时,绕x轴的基底气动弯矩分量为横风向响应,绕y轴的为顺风向响应;当风向角为90°时,绕y轴的基底气动弯矩分量为横风向响应,绕x轴的为顺风向响应。由于本文研究对象主要针对长边迎风或短边迎风的横风向风效应,因此下文数据分析讨论只针对0°的Mx和90°的My的横风向响应展开。
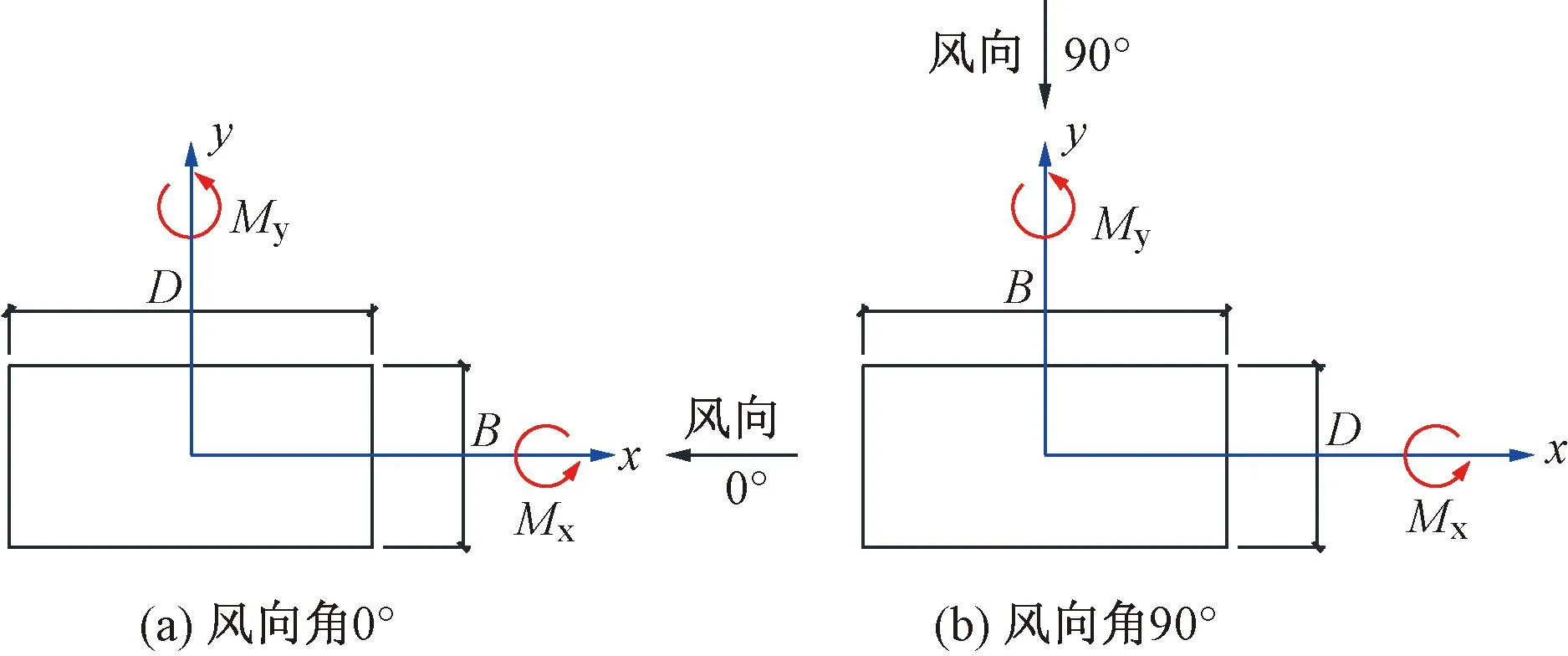
图3 试验风向角及顺、横风向基底气动弯矩方向定义示意图
1.3 建筑原型结构动力特性及风场参数
本文计算所用的结构周期是基于已有工程经验和荷载规范估计得到的,假定振型沿高度呈线性分布,结构质量为1700 kg/m2,7种深宽比下,模型前3阶振型自振周期见表1,由表可得,第1阶和第3阶振型保持不变,第2阶振型随深宽比的增大而减小,相应阻尼比取5%。并通过周期比和阻尼比的敏感性分析,考虑周期和阻尼比对结构风荷载的影响,基本风压参照深圳市地区选取,其100年和50年重现期风压分别为0.90kPa和0.75kPa。
2 数据处理及分析方法
2.1 数据预处理
为方便比较各工况的试验数据,并在模型和原型间进行换算,风洞试验中采用以下无量纲形式来描述结构基底气动弯矩(扭矩):
(1)
在采用HFFB试验时,天平模型系统的共振抖振会导致信号畸变,因此必须加以修正[11],本文采用文献[12]的方法对被测信号进行修正。图4为D/B=3∶1工况修正前后0°风向角下基底气动弯矩功率谱密度的比较。图中,SMA,i(f)为试验测得的基底气动弯矩功率谱密度,qM为参考高度处的参考弯矩,f为频率。
2.2 结构风荷载的计算方法
根据随机振动理论[13],将试验测得的基底气动弯矩功率谱密度SMA,x(f)(为简化描述,以下统一用SMA(f)表示)乘以结构机械导纳|H(f)|2就可以得到修正后的基底气动弯矩功率谱密度SMD(f)和基底气动弯矩均方根值σMD,见式(2)~(5)。
SMD(f)=|H(f)|2SMA(f)
(2)
(3)
(4)
(5)
对于0°和90°风向角的横风向基底气动弯矩,其平均值为0,故有:
(6)
3 主要结果
3.1 深宽比的影响及与荷载规范结果的比较
首先用B类地貌下的风洞试验数据计算分析不同平面深宽比(D/B)的50年重现期超高层建筑横风向风荷载的变化规律并和荷载规范计算结果进行对比,见图5。由图可见:
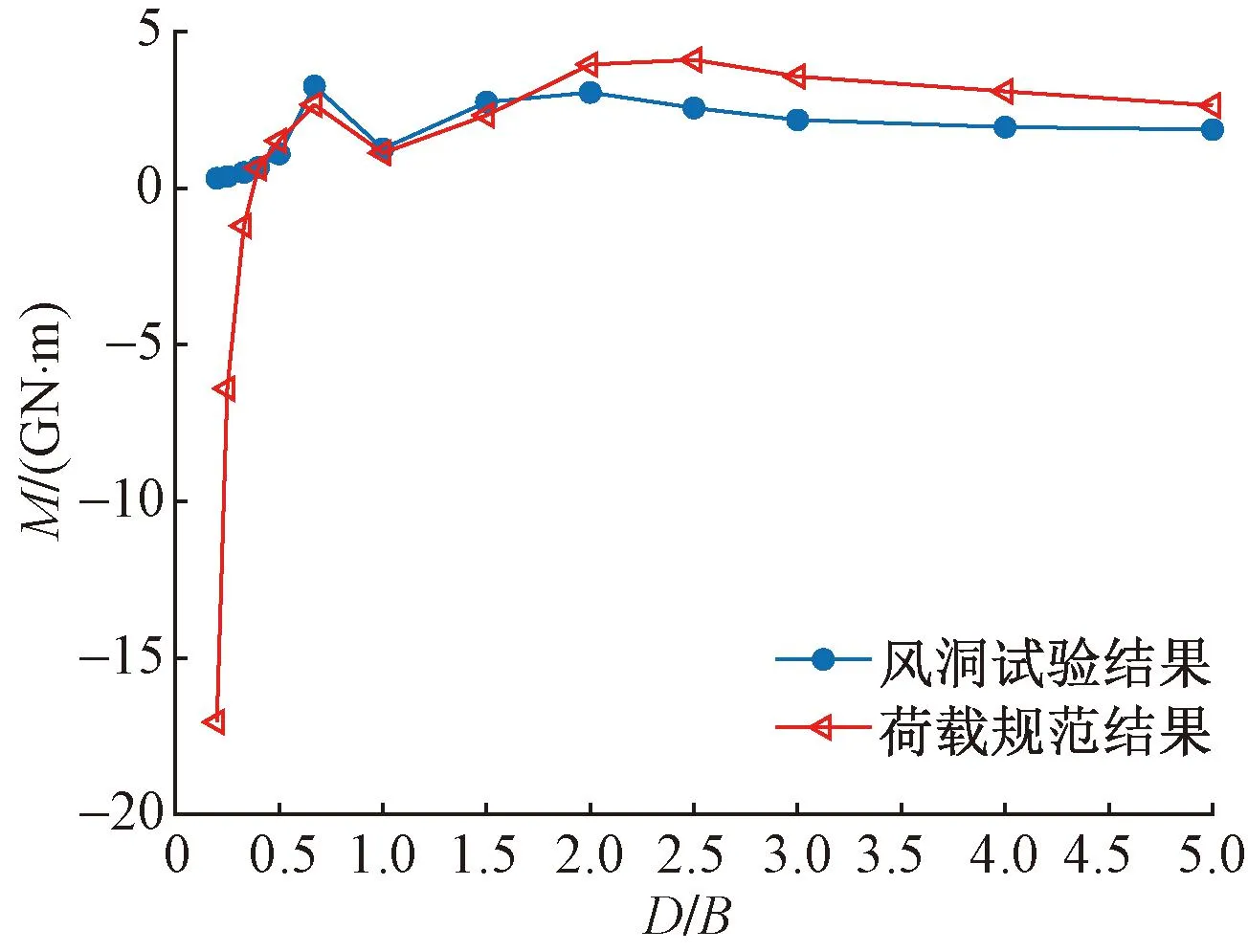
图5 荷载规范计算与风洞试验结果对比
(1)D/B=1∶1.5和D/B=1.5∶1工况的横风向荷载最大,但D/B=1的横风向荷载相比较小,为1.26GN·m,和荷载规范计算结果相近。结合图6横风向气动弯矩功率谱密度可知,D/B=1工况下的50年重现期折算频率较其他两个深宽比工况更远离旋涡脱落谱峰频率,结构横风向风荷载不显著,横风向气动力作用减小,基底气动弯矩响应降低。
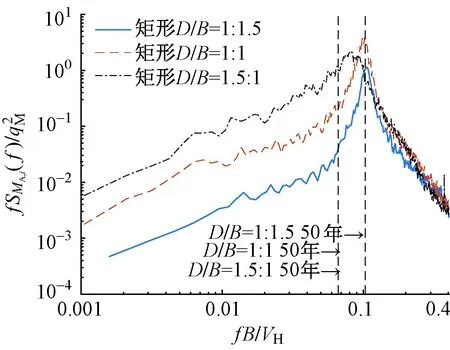
图6 横风向气动弯矩功率谱密度曲线
(2)对于D/B=2的工况,当风向角为0°时,Mx为3.05 GN·m,当风向角为90°时,此时深宽比为0.5,My为1.09 GN·m,可见其窄边迎风的横风向风荷载要比宽边迎风的相应结果高出180%,且深宽比大于2的各工况下也有类似变化规律。
(3)在D/B≤0.67时,风洞试验得到的横风向基底气动弯矩随着D/B的减小而减小;在D/B≥2时,风洞试验得到的横风向基底气动弯矩随着D/B的增大而减小,但其值均不同程度比荷载规范计算结果小,如表2所示,最大误差可达38.9%。
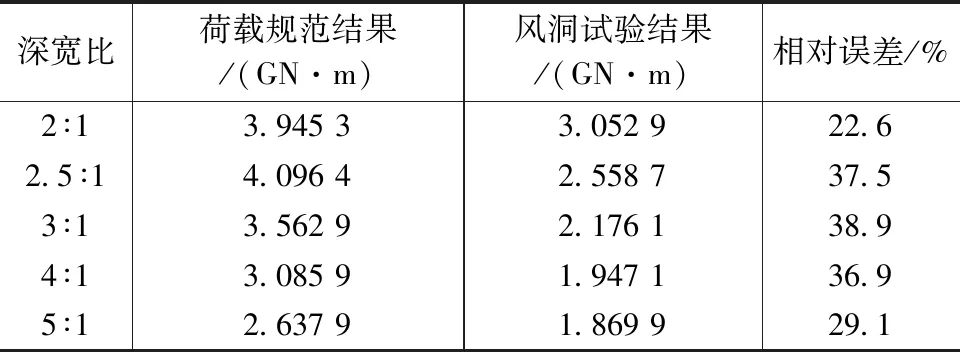
表2 荷载规范结果与风洞试验结果对比
(4)在0.5≤D/B<2时,基于荷载规范而得到的横风向基底气动弯矩与风洞试验结果具有较好的一致性;当D/B≤0.33时,荷载规范结果出现急剧递减的基底气动弯矩负值,主要是该取值超出了荷载规范拟合公式的取值范围,且由于D/B≤0.33时对应的风荷载均比较小,不起控制作用,在抗风设计中可以忽略。
3.2 湍流度的影响
湍流度对横风向风荷载的影响机理较为复杂,其将影响结构迎风前缘的分离和再附,从而影响横风向气动力作用。对比B、C两类地貌下,50年重现期结构的横风向基底气动弯矩均方根值σMD随湍流度的变化,见图7。由图可见:多数深宽比情况下,B类地貌的σMD要高于C类地貌,B类地貌下σMD的最大值约为C类地貌的2.33倍。不规则点出现在D/B=1工况,该工况下C类地貌的σMD比B类的提高了9.82%。两种地貌下的σMD在D/B>2后,随着D/B的增大呈现单调递减的趋势,不同的是C类地貌先于B类地貌出现σMD减小现象,原因是湍流度的增加使得侧风面分离气流更早再附,横风向气动力整体减小。
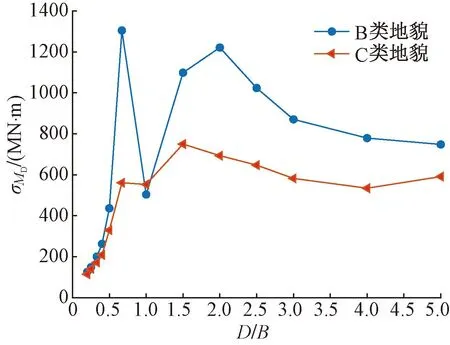
图7 横风向基底气动弯矩均方根值随湍流度变化
进一步分析B、C类地貌对σMD的影响:
(1)当D/B≤0.5时,B、C地貌下的σMD基本保持一致,原因是此时为宽边迎风,横风向气动力主要受旋涡脱落控制,湍流度对旋涡脱落影响较小。
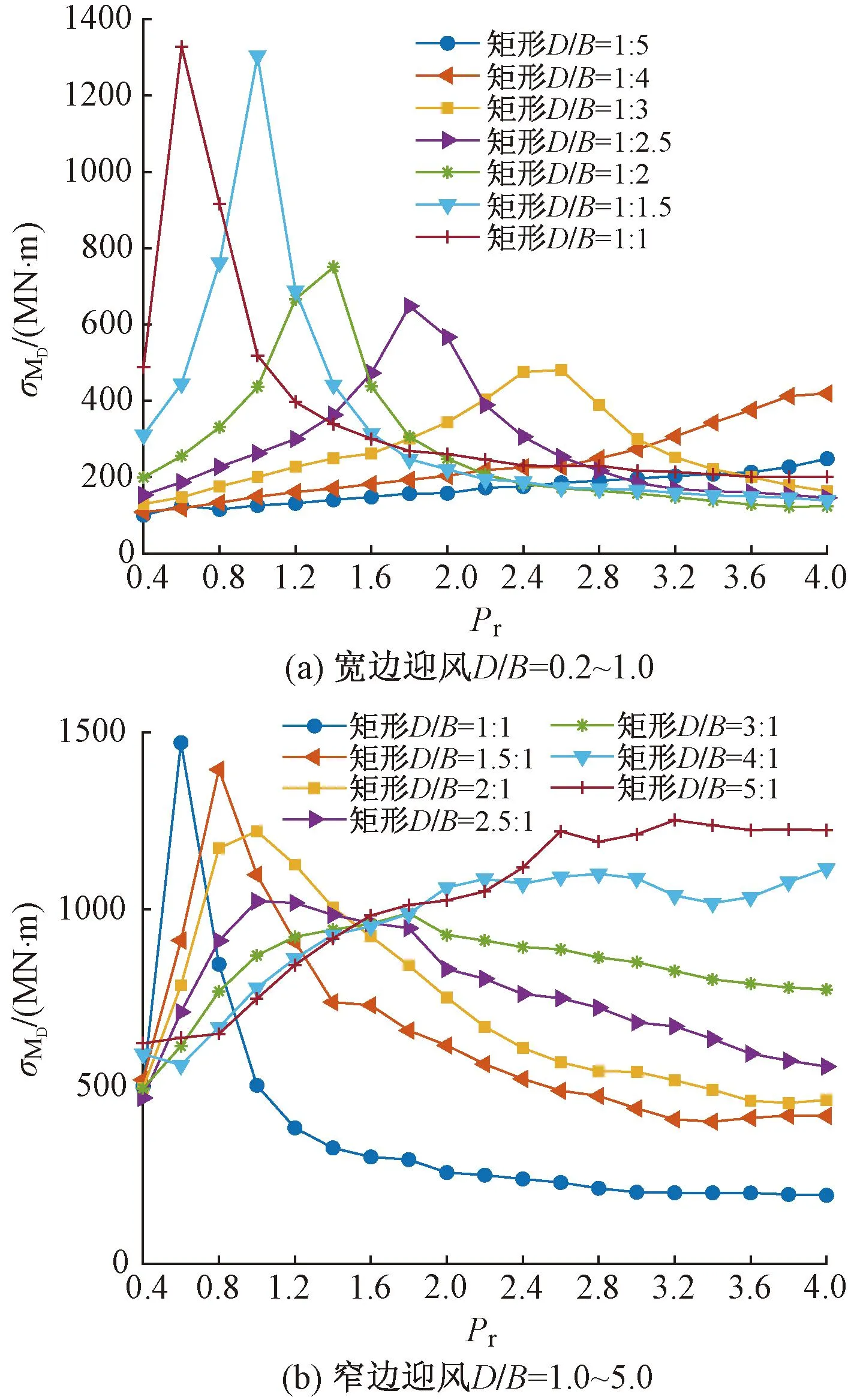
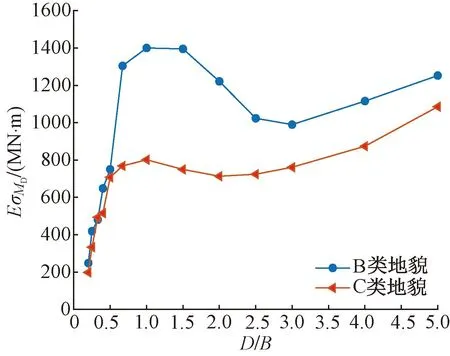
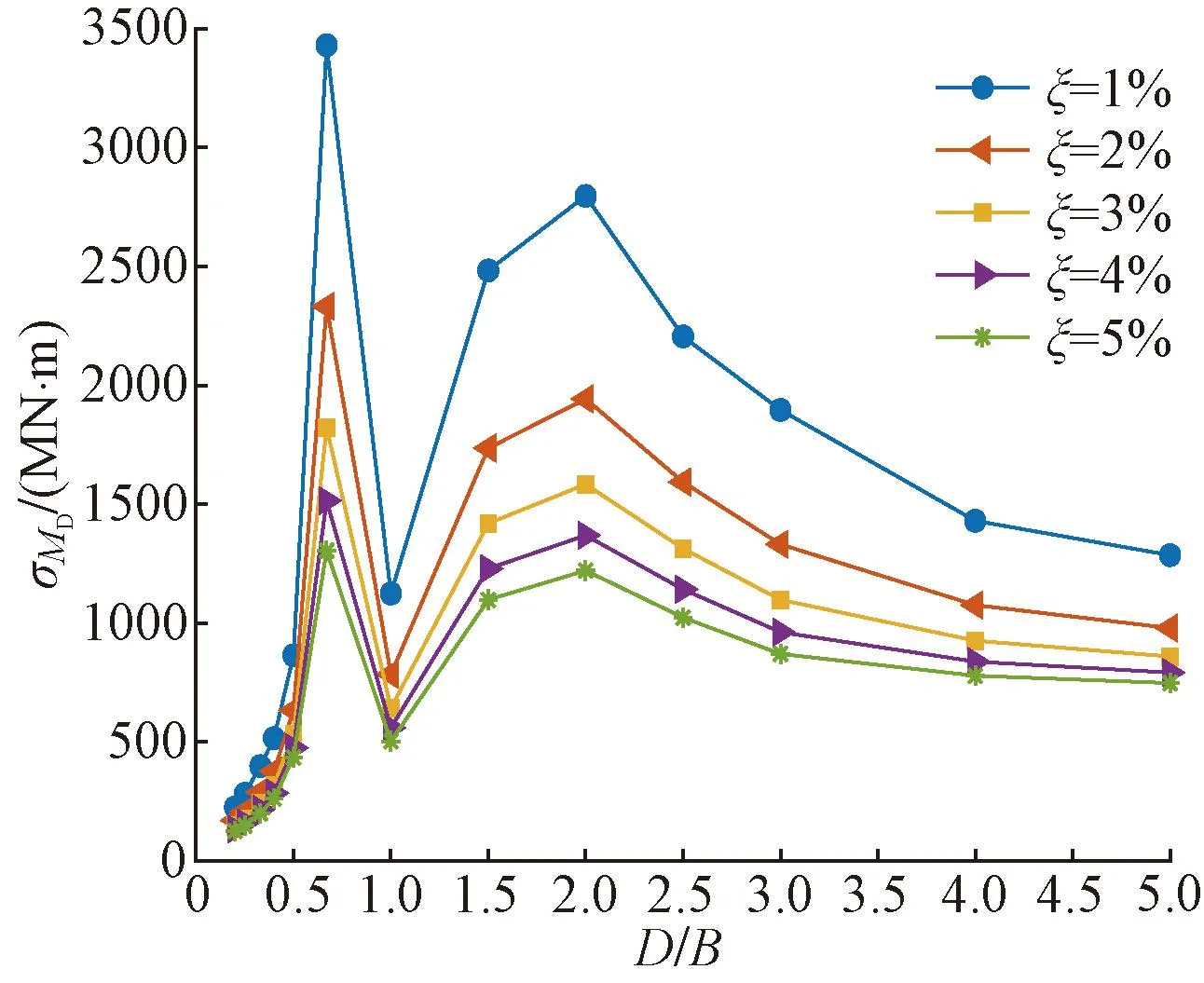
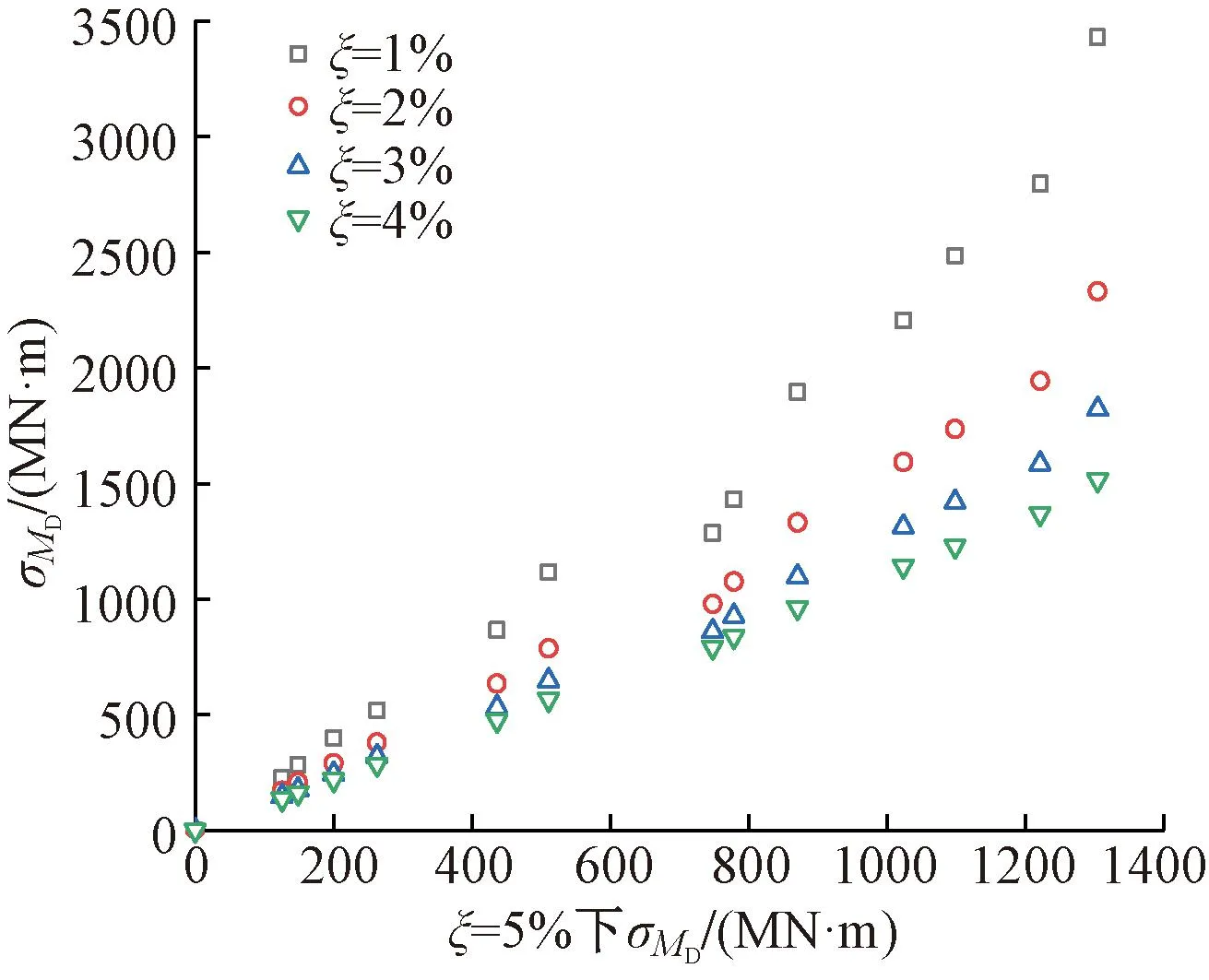
(2)当0.5 图8 横风向基底气动弯矩功率谱密度 (3)当D/B≥2时,B类地貌下的σMD呈现梯度式递减,当D/B=2、D/B=2.5、D/B=3、D/B=4、D/B=5时,C类地貌下的σMD比B类地貌分别降低了43.24%、36.79%、33.15%、31.41%、21%,可以看出,随着D/B的增大,B、C两类地貌下的σMD偏差逐渐减小且两条曲线有重合的趋势。 以上仅仅给出由特定结构周期和基本风压对结构横风向荷载的影响,这不可避免会得到一些在表面上看似具有一定困惑性的结论,如图7所示的D/B=1时,两种地貌的风荷载相对偏小且出现C类的反超B类的问题。本文计算所采用的结构周期是根据已有工程和荷载规范建议大致估算得到的,实际原型结构的自振周期在此基础上应该有所变化,为更全面评价不同D/B对σMD的影响,本节进一步分析不同D/B在不同结构周期下σMD的变化规律。采用周期比Pr,定义为实际结构周期与本文计算周期之比,取0.4~4,来描述周期的变化,基于AtiHFFB测力分析软件修改自振周期、模态阻尼比等结构动力特性参数即可考虑周期和阻尼比的敏感性,Pr的变化同样也可以反映风速的变化,可以理解是考虑风速变化对σMD的影响。图9为50年重现期基本风压作用下,B类地貌下宽边和窄边迎风时σMD随周期比变化的结果。 图9 横风向基底气动弯矩均方根值随周期比变化 宽边迎风时,由图9(a)可知,横风向基底气动弯矩均方根最大峰值出现在D/B=1工况下Pr=0.6处,为1328.72 MN·m,且横风向风荷载对周期比的敏感度随深宽比的减小逐渐减弱。当D/B减小至0.2时,σMD在全周期变化范围内较为平稳,可见其对周期比变化最不敏感。 窄边迎风时,由图9(b)可知,D/B=1.5的σMD在Pr=1附近变化幅度较大,在增大周期(提高风速)的情况下能显著降低横风荷载。且当1≤D/B≤3时,越往长周期发展,σMD下降幅度逐渐减弱。D/B=4、5的σMD对周期比敏感度较强,整体上呈现波动递增的趋势,横风向基底气动弯矩均方根值在Pr>2后超过其他深宽比工况。 图9更加完整地描述了不同深宽比建筑的σMD的变化规律,但结果过于复杂且规律性较弱,为此将不同Pr下的σMD作包络处理,图10给出了两类地貌不同Pr下的σMD的包络值EσMD随D/B变化的曲线。由图可见: 图10 不同周期比横风向基底气动弯矩均方根包络值随深宽比变化 (1) 在B、C两类地貌下,EσMD的最大值均出现在D/B=1的时候,这个结果和一般认为正方形平面超高层建筑气动性能最差、风荷载最大的认知相符合,且B类地貌的EσMD比C类地貌高出42.75%。 (2) 对于不起控制性作用的D/B≤0.5,两种地貌下的EσMD差别不明显;风荷载最为显著的深宽比范围为0.5~2,但敏感度随地貌的粗糙度的增加而减弱。 (3) 在D/B≥2.5后,EσMD随D/B单调递增,B类地貌下EσMD大致要比C类地貌的高出15%~40%。 结构模态阻尼比对横风向风荷载的影响主要体现在结构风致振动上,一定的结构阻尼能够耗散结构在风荷载作用下的振动能量,故结构阻尼越大结构振动峰值越小。图11给出了B类地貌下50年重现期不同阻尼比ξ的σMD随D/B的变化曲线,阻尼比变化范围为1%~5%。试验结果表明:结构模态阻尼比对结构风荷载有很大的影响,各深宽比工况的σMD对阻尼比变化较为敏感。 图11 不同阻尼比下基底气动弯矩均方根值随深宽比变化 随着阻尼比的减小,σMD明显提高,且σMD递增的幅度由小变大,当D/B=1∶1时,ξ=1%的σMD比ξ=5%的相应结果增大了123.39%,而在D/B=0.67下σMD的升幅更为显著。当ξ=2%时,σMD为2331.93 MN·m,比ξ=5%的相应结果增大了78.76%,且其他阻尼比ξ=1%、ξ=3%、ξ=4%的σMD较ξ=5%工况分别增大了162.98%、39.72%、16.16%,偏差逐渐减小。这侧面反映了实际工程中利用准确的阻尼比计算结构风荷载的重要意义,同时也说明了提高阻尼比有利于降低结构的横风向风荷载,当阻尼比增大到一定程度时,横风效应的这种减小作用趋于平缓。 为了进一步考察阻尼比对横风向风荷载的影响,以ξ=5%的σMD作为参照对象,将全部深宽比工况的σMD在不同阻尼比下的结果进行逐一对比,结果见图12。 图12 不同阻尼比下基底气动弯矩均方根值对比 由图可见:ξ=2%、ξ=3%、ξ=4%下σMD的数据结果相近,结果相关性较强,采用乘幂函数形式对不同阻尼比下的σMD进行拟合,得到ξ=1%~4%下的拟合优度R2分别为0.97、0.98、0.99、0.99,与R2=1相近,回归直线拟合程度较高,进一步说明了横风向风荷载对阻尼比变化较为敏感。 (1)当0.5≤D/B<2时,基于荷载规范而得到的横风向基底气动弯矩与风洞试验结果较为吻合;当D/B≥2时,横风向基底气动弯矩随着D/B的增大而减小,荷载规范结果不同程度高于风洞试验结果,最大相对误差出现在D/B=3工况,风洞试验结果比荷载规范结果小38.9%。 (2)对横风向风荷载影响最敏感的深宽比范围为0.5~2,但敏感度随地貌的粗糙度的增加而减弱,B类地貌的横风向风荷载比C类地貌高出42.75%;在D/B≥2.5后,横风向风荷载随D/B单调递增,B类地貌下风荷载大致要比C类地貌的高出15%~40%。 (3)结构横风荷载对阻尼比较为敏感,采用2%阻尼比的风荷载会比5%阻尼比的荷载最大高出78.76%,且不同阻尼比下的横风向基底气动弯矩均方根值相关性较强,在实际工程中利用准确的阻尼比计算结构风荷载具有重要意义。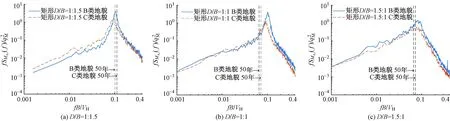
3.3 周期比的影响
3.4 阻尼比的影响
4 结论
