透镜成像反向学习的精英池侏儒猫鼬优化算法

贾鹤鸣，陈丽珍，力尚龙，刘庆鑫，吴 迪，卢程浩

1.三明学院 信息工程学院，福建 三明 365004

2.海南大学 计算机科学与技术学院，海口 570228

3.三明学院 教育与音乐学院，福建 三明 365004

随着科技的不断发展，工程优化问题变得越发复杂，亟需寻找更为有效的求解算法。因此许多学者受自然界中生物的习性和事物的自然规律启发提出了元启发式算法，并将其应用于工程优化问题求解。近年来提出的元启发式算法主要有算术优化算法（arithmetic optimization algorithm，AOA）[1]、正余弦优化算法（sine cosine algorithm，SCA）[2]、灰狼优化算法（grey wolf optimization，GWO）[3]、樽海鞘群优化算法（salp swarm algorithm，SSA）[4]、蛇优化算法（snake optimizer，SO）[5]、䲟鱼优化算法（remora optimization algorithm，ROA）[6]、黏菌优化算法（slime mould algorithm，SMA）[7]和粒子群优化算法（particle swarm optimization，PSO）[8]等。元启发式算法因具有稳定性强且易于实现等优点，常被人们应用于工程设计问题求解。

侏儒猫鼬优化算法（dwarf mongoose optimization algorithm，DMO）是由Agushaka 等[9]于2022 年提出的一种群体智能优化算法。其灵感来源于侏儒猫鼬的群体觅食行为，但DMO 算法依然存在收敛速度慢及易陷入局部最优的缺点。透镜成像反向学习策略是基于透镜成像原理提出的一种改进策略[10]，能够增强算法跳出局部最优的能力，从而提高算法的寻优性能。周鹏等[11]提出一种改进的平衡优化器算法，通过透镜成像反向学习策略来提高算法的搜索能力，降低算法在迭代后期陷入局部最优的概率。刘庆鑫等[12]提出了一种多策略融合的䲟鱼优化算法，利用布朗运动提高算法的探索能力，再引入透镜成像反向学习策略，进一步提高算法跳出局部最优解的能力，使算法的探索能力和开发能力更加平衡。

为了提高DMO算法的收敛速度，增强其探索能力，本文提出了融合透镜成像反向学习的精英池侏儒猫鼬优化算法。首先，采用透镜成像反向学习策略，降低算法陷入局部最优的概率，增强算法全局探索的能力；然后，在阿尔法组成员觅食的时候引入精英池策略，避免了算法迭代后期个体向食物源聚集的问题，进一步降低陷入局部最优的概率。基于13个标准测试函数的实验结果表明，IDMO 算法具有更好的寻优性能和鲁棒性。最后，通过对汽车碰撞优化问题的求解，验证IDMO 算法对工程问题同样具有较高的适用性。

1 侏儒猫鼬优化算法

DMO算法是模拟侏儒猫鼬半游牧式生活的一种元启发式算法。侏儒猫鼬通常生活在一个母系社会的家族群体中，主要有觅食、侦察和保姆三种社会职能。侏儒猫鼬以集体觅食和侦察而闻名，由雌性首领引导种群进行食物源的搜寻。一旦满足保姆交换条件，即当阿尔法组未能寻找到合适的食物时，将交换阿尔法组和保姆组的成员，且阿尔法组同时进行觅食和寻找睡眠丘。

1.1 阿尔法组

1.1.1 雌性首领的产生

雌性首领在阿尔法组中产生，阿尔法组中每个雌性个体成为首领的概率为α，计算公式如下：

其中，fiti是第i个个体的适应度，N是侏儒猫鼬种群中个体的总数。阿尔法组的个体数量为n′,bs为保姆的数量。

1.1.2 阿尔法组成员觅食

阿尔法组成员将共行并进行觅食，食物源的候选位置由式（2）给出：

其中，Xi+1是找到的食物源新位置，Xi为雌性首领的当前位置，phi是均匀分布在[-1,1]之间的随机数，本文peep选取为2，Xrand是阿尔法组中的随机个体。

1.2 保姆交换条件

保姆交换条件是用于重置阿尔法组和保姆组中的猫鼬个体。当阿尔法组成员未能搜寻到合适的食物时，认为阿尔法组成员能力不足，将交换阿尔法组和保姆组的成员。交换条件满足后，阿尔法组将同时进行觅食和寻找睡眠丘，计算公式如下：

其中，Xb为交换后个体的新位置，ub和lb分别为搜索空间的上界和下界，rand是0到1之间的随机数。

保姆交换后的觅食行为由公式（2）实现。睡眠丘是猫鼬休息的场所，而猫鼬不会回到之前的睡眠丘，这种生活模式能够避免搜索区域被过度开发的问题。新搜寻到的睡眠丘的数学模型如下：

其中，Xsm为新的睡眠丘的位置，M是决定猫鼬移动到新睡眠丘的方向向量，φ是睡眠丘的平均值，计算公式如下：

其中，smi代表睡眠丘值：

CF表示猫鼬种群移动能力的参数，它会随着迭代次数线性递减，计算公式如下：

其中，t为当前迭代次数，T为最大迭代次数。

2 改进的侏儒猫鼬优化算法

2.1 基于透镜成像原理的反向学习策略

反向学习是通过计算当前位置的反向解，从而扩大搜索范围的一种改进策略。在群智能优化算法中采用反向学习策略，可以在一定程度上提升算法的寻优能力；但通过反向学习求得的反向解是固定的，若个体已经陷入局部最优，且其反向解劣于当前解，则反向学习策略无法使该个体跳出局部最优。而透镜成像反向学习可以有效解决上述问题。

透镜成像反向学习策略如图1所示，以二维空间为例，[a,b]为解的搜索范围，y轴表示凸透镜。假设有一物体P，高度为h，在x轴上的投影为x；该物体通过凸透镜成像在凸透镜的另一侧呈现出一个倒立的实像P*，高度为h*，在x轴上的投影为x*。由凸透镜成像原理可得：

图1 透镜成像反向学习策略示意图Fig.1 Opposition learning strategy based on lens image

令k=h/h*，则式（9）可改写为：

式（10）为凸透镜成像反向学习策略的反向解的求解公式，当k=1 时，式（10）可化简为：

该式即为反向学习的求解公式。

由上述可知，反向学习就是特殊的透镜成像反向学习，采用反向学习得到的是固定的反向解。而通过调整k的大小，可以在透镜反向学习中获得动态变化的反向解，进一步提升算法的寻优能力。本文中采用的k值计算公式如下：

2.2 精英池策略

精英池策略是用于提高算法探索能力的一种选择策略[13]。其将当前最优的三个个体和种群中适应度值前一半个体的加权平均位置储存在精英池中，种群中前一半的个体在进行位置更新时都会随机选择精英池中的一个个体作为食物源；该策略有效避免了种群因只有一个食物源而陷入局部最优的问题，提高了算法的探索能力。

原始DMO 算法具有较强的全局探索能力，但由于仅确定一个食物源会导致猫鼬种群出现向一个食物源聚集的问题，导致算法易陷入局部最优，所以本文采用上述策略来解决该问题。选择当前适应度值最优的三个个体和阿尔法组全部成员的加权平均位置存储在精英池中。三个最优个体能够帮助阿尔法组进行探索，加权平均位置则代表整个优势种群的进化趋势，有利于算法进行开发。随后将随机选择精英池中的一个个体进行觅食，从而增强了原始算法的探索能力。精英池策略如图2所示。

图2 精英池策略示意图Fig.2 Schematic diagram of elite pool strategy

图2 中，Xbest1、Xbest2和Xbest3分别为当前种群适应度值最优的前三个个体，Xmean是阿尔法全部成员的加权平均位置，其计算公式如下：

调整后的食物源的更新公式如下：

其中，Xelite是精英池策略选择的个体位置。

2.3 IDMO的伪代码

融合透镜成像反向学习的精英池侏儒猫鼬优化算法的伪代码如下所示：

2.4 IDMO的流程图

融合透镜成像反向学习的精英池侏儒猫鼬优化算法实现流程如图3所示。

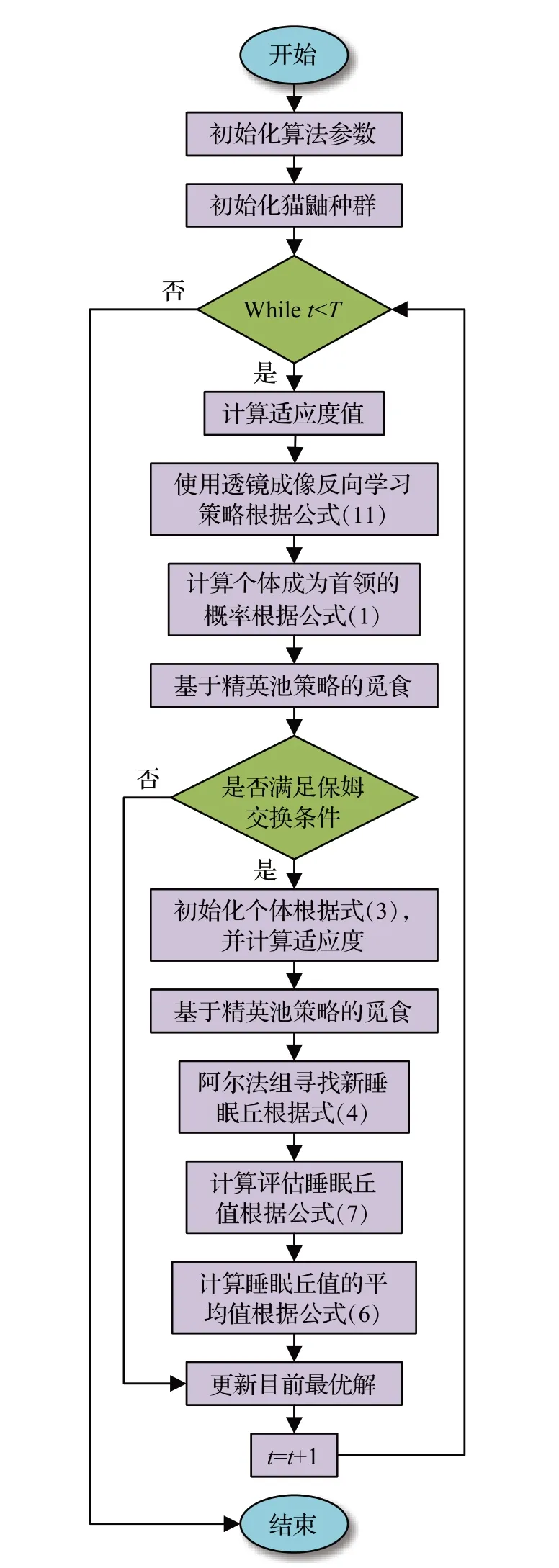
图3 IDMO算法流程Fig.3 Flow chart of IDMO

2.5 IDMO的时间复杂度分析

时间复杂度直接反映算法的运算效率，间接反映算法的收敛速度，是体现算法性能的重要因素。

在DMO 算法中，假设种群规模为N，个体维度为n，初始化算法参数所需时间为η0，每一维上产生均匀分布随机数的时间为η1，则初始化种群阶段的时间复杂度为：

进入迭代后，迭代次数为T，计算每个猫鼬个体适应度值的时间为f(n)，根据公式（1）计算阿尔法组中雌性个体成为首领的概率所需时间为η2，则此阶段的时间复杂度为：

在阿尔法组成员觅食阶段，阿尔法组的个体数量为n′，在公式（2）中，phi为均匀分布的随机数，每个个体的每一维都各不相同，其生成时间均与η1一致，选取peep的时间为η3且由公式（2）进行每一维食物源位置更新的时间为η4。则该阶段的时间复杂度为：

满足保姆交换条件后，在公式（3）中，rand是随机数且每个个体的每一维都各不相同，其生成时间均与η1一致。公式（3）初始化所需时间为η5。在公式（4）中，计算M、φ和smi所需时间分别为η6、η7、η8，计算phi和rand所需时间与上述一致。则该阶段的时间复杂度为：

综上所述，DMO的总时间复杂度为：

在改进算法IDMO中，算法的种群规模、个体维度、初始化参数时间以及每一维上产生均匀分布随机数的时间均与DMO 算法一致，所以初始化种群阶段的时间复杂度为：

进入迭代后，迭代次数为T，计算每个猫鼬个体适应度值的时间和计算阿尔法组中雌性个体成为首领的概率所需的时间均与DMO 算法一致，则此阶段的时间复杂度为：

设由公式（12）产生k的时间为t1，由公式（14）产生的阿尔法组中按适应度值降序排列的权重系数ωi的时间为t2，由公式（13）产生的Xmean的时间为t3，由公式（15）产生的Xi+1的时间为t4。则该阶段的时间复杂度为：

综上所述，IDMO算法的总时间复杂度为：

由此可知，与DMO算法相比，本文IDMO算法并未增加时间复杂度，执行效率没有下降。

3 实验仿真与分析

本次实验的实验操作系统为Windows11 系统，11th Gen Intel®CoreTMi7-11700 2.50 GHz，16.00 GB内存，实验仿真过程在Matlab 2021a 中实现。为了验证IDMO 算法的性能，本文选取了13 个标准测试函数对IDMO算法的性能进行测试[14]。表1为13个标准测试函数的基本信息。其中，F1～F5 是单峰函数，只有一个全局最优解，对算法的开发能力进行检验。F6～F10 是多峰函数，有一个全局最优解和多个局部最优解，可对算法的全局搜索能力进行检测。F11～F13 是固定维度多峰函数，对算法探索和开发能力之间的平衡性进行验证。通过上述三种不同类型的测试函数，充分验证算法的寻优性能。

表1 标准测试函数Table 1 Benchmark functions

3.1 对比算法与参数设置

为充分验证本文提出的IDMO算法的性能，选取了7种算法进行对比，分别是DMO[9]、AOA[1]、SCA[2]、GWO[3]、SSA[4]、SO[5]和ROA[6]，这些算法已被证实具有良好的寻优性能。为了更准确地验证IDMO 算法与比对算法的优劣性，统一设定种群规模N=30，维度D=30，最大迭代次数500 次，各算法独立运行30 次。选取平均值、标准差与Wilcoxon 秩和检验作为评价标准。平均值与标准差越小，算法的性能越好。表2为各对比算法的参数设置。

表2 算法参数设置Table 2 Algorithm parameter setting

3.2 求解精度分析

IDMO算法及其对比算法的最优适应度值、平均适应度值和适应度值标准差如表3所示。Best为最优适应度值，Mean 为平均适应度值，Std 为适应度值标准差。函数F1～F5 为单峰函数；在求解函数F1 时，IDMO 算法得到了理论最优值；在求解函数F2和F4时，IDMO算法均得到了理论最优值，明显优于DMO和其他对比算法；在求解函数F3时，IDMO算法得到了理论最优值，ROA虽得到了最优适应度值和适应度值标准差的理论最优值，但其稳定性较差；在求解函数F5时，IDMO算法得到了最优适应度值的理论最优值，SSA虽得到了最佳的平均适应度值和适应度值标准差，但其最优适应度值明显较差，表明IDMO 算法跳出局部最优的能力较强；由此可知，引入透镜成像反向学习和精英池策略使得IDMO算法的局部开发能力显著提升，算法收敛精度有所提高。函数F6～F10 为多峰函数；在求解函数F6 和F8 时，IDMO 算法和ROA 均得到了理论最优值，SO 则得到了最优适应度值的理论最优值，但其稳定性较差；在求解函数F7、F9和F10时，IDMO算法均得到了最优值，明显优于DMO和其余对比算法；由此可知，IDMO算法的探索能力优于其他对比算法。函数F11～F13 为固定维度多峰函数；在求解函数F11时，IDMO算法虽未取得最优的适应度值标准差，但其最优适应度值和平均适应度值都是最优的；在求解函数F12和F13时，IDMO算法均得到了最佳的最优适应度值、平均适应度值和适应度值标准差，GWO 和ROA 均得到最佳的最优适应度值，但平均适应度值和适应度值标准差略差于IDMO算法；这验证了IDMO算法的收敛精度明显更高，且搜索能力和开发能力的平衡明显更优。

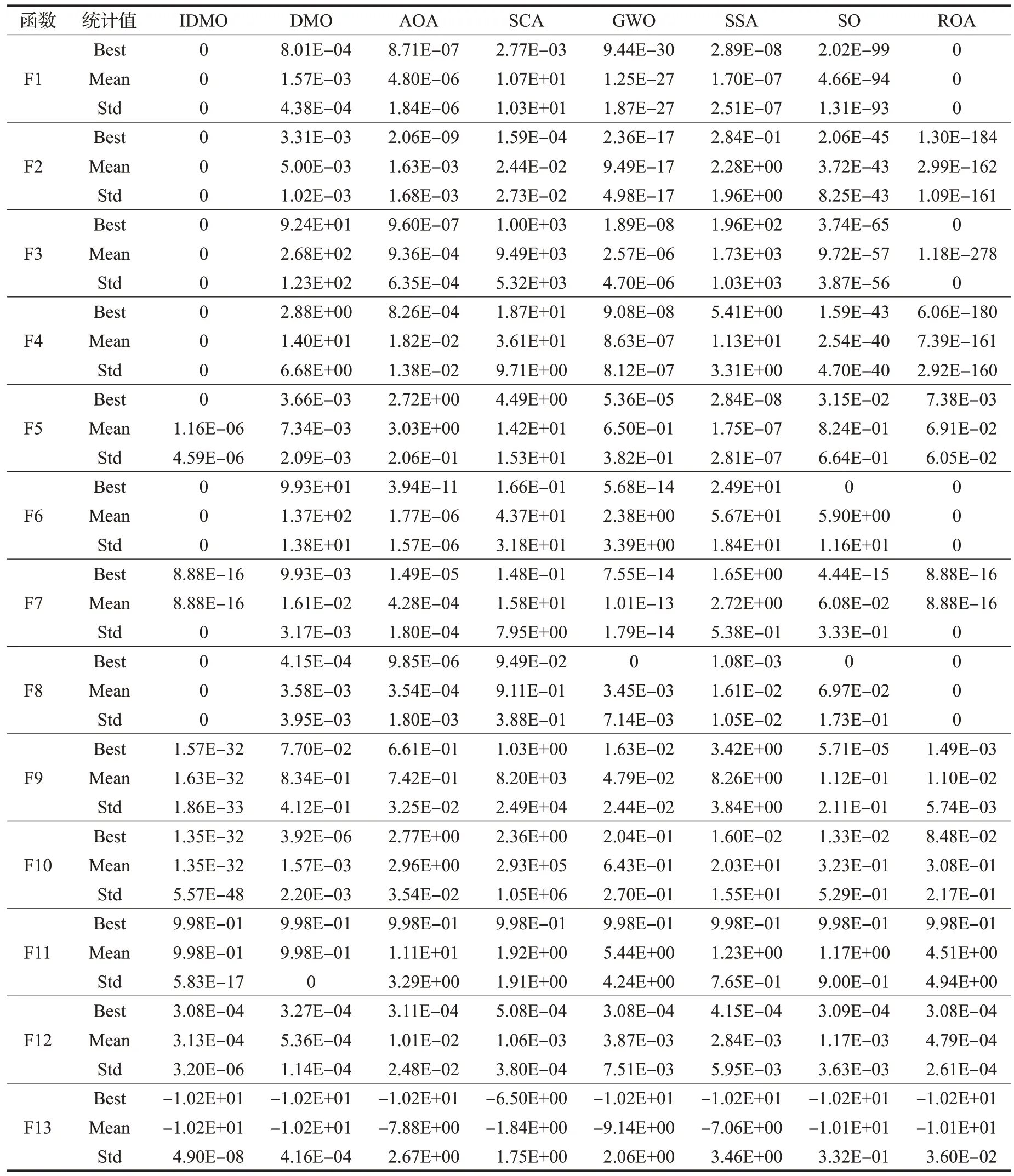
表3 各算法标准函数测试结果Table 3 Test results of benchmark functions of each algorithm

3.3 收敛曲线分析

为了更直观地反映各算法的收敛速度和跳出局部最优的能力，本文给出部分测试函数的收敛曲线如图4所示。对于函数F1、F2、F3和F4，DMO、AOA、SCA、GWO、SSA和SO的收敛精度都较低；ROA在函数F1和F3中，收敛精度较高，但收敛速度过慢，在函数F2和F4中，收敛精度较低；IDMO 算法在迭代一开始就快速收敛，且找到了理论最优值。对于函数F5，IDMO算法在迭代初期快速收敛，收敛精度明显更高。单峰函数的收敛曲线证明了IDMO 算法引入透镜成像反向学习策略和精英池策略有效提高了收敛能力和全局探索能力。对于函数F7、F8、F9 和F10，IDMO 算法在迭代初期快速收敛，且在函数F8 中得到理论最优值，AOA 在函数F7、F9 和F10 中长期陷入局部最优。多峰函数F7、F8、F9 和F10体现了IDMO 算法具有卓越的探索能力。对于固定维度多峰函数F12 和F13，IDMO 算法在迭代前期快速收敛，寻优时间均少于其他算法；在函数F13 中，AOA、SCA、GWO、SSA、SO、RAO均多次陷入局部最优，DMO算法的收敛速度略逊于IDMO算法；体现了IDMO算法探索和开发之间平衡性的优越。

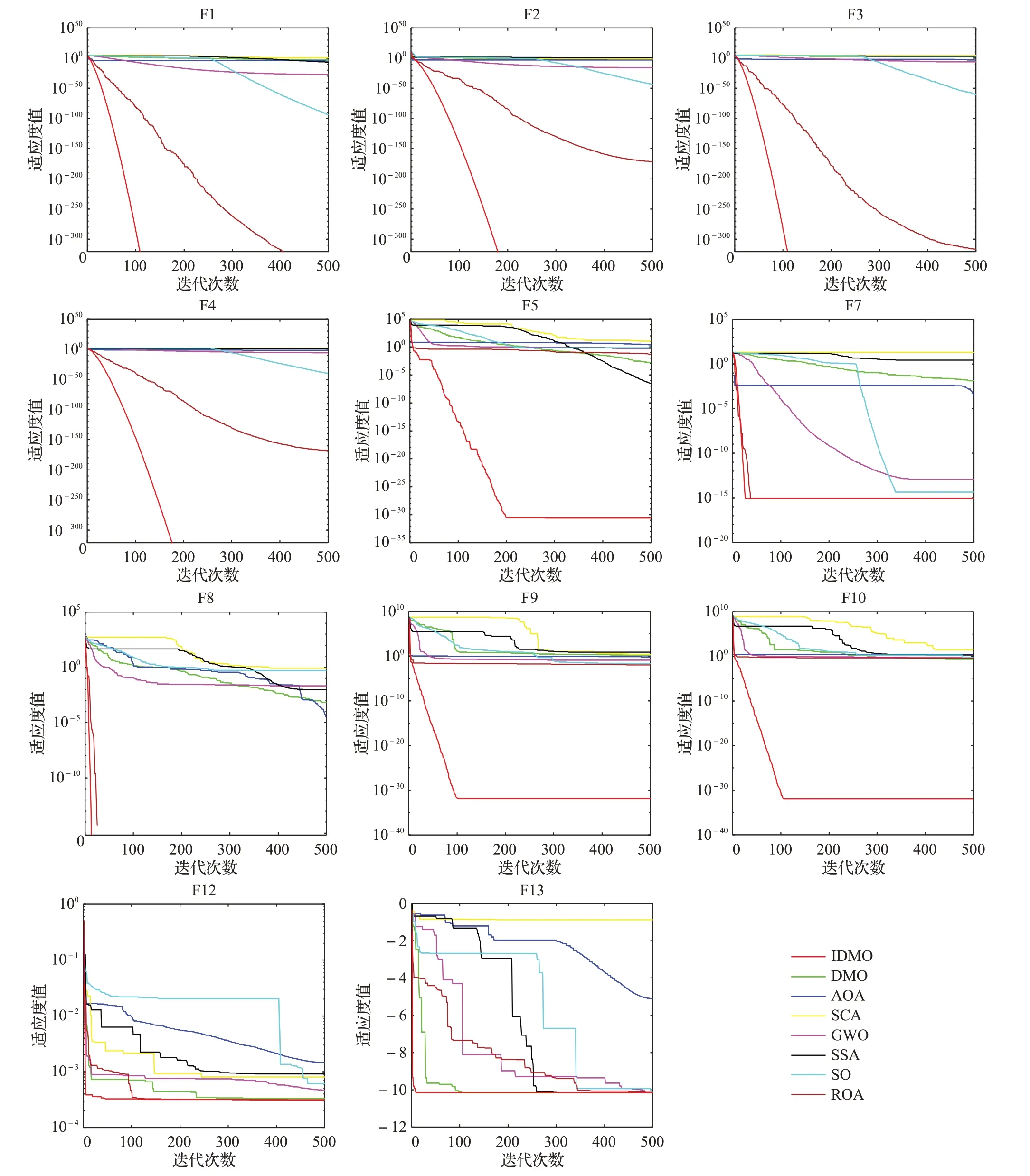
图4 部分测试函数的收敛曲线Fig.4 Convergence curve of partial test function

3.4 Wilcoxon秩和检验

为了充分验证算法的鲁棒性，本文采用Wilcoxon秩和检验来验证各算法整体结果的显著性差别。Wilcoxon秩和检验在5%的显著性水平下进行，当p<5%时，表明两种对比算法存在显著差异，反之表明两种算法的寻优性能差异不大。因此，本文将8 种算法作为样本，各算法独立求解15 次，设定种群个数N=30，维度D=30，测试13 个标准测试函数判断IDMO 算法所得结果与7个对比算法所得结果的显著性区别。Wilcoxon 统计检验p值结果如表4所示。由表4可知，大部分p值均小于5%，说明IDMO 算法与其余比对算法之间存在显著差异。

表4 各算法Wilcoxon秩和检验结果Table 4 Wilcoxon rank sum test results of each algorithm

通过综合分析各算法标准函数测试结果、部分测试函数的收敛曲线和各算法Wilcoxon秩和检验结果，可得出如下结论：IDMO 算法的局部和全局能力均显著提升，且优于原始DMO 和SSA 等对比优化算法，具有更佳的收敛速度、收敛精度以及稳定性。

4 汽车碰撞优化问题求解

汽车碰撞优化问题的设计目的是实现汽车轻量化，即在保证汽车安全性能的前提下，最大程度地降低汽车的整备质量[15]。该问题包含了11个决策变量和10个约束条件，其中决策变量分别是B 柱内部厚度、B 柱钢筋厚度、地板内侧厚度、横梁厚度、门梁厚度、门带线钢筋厚度、车顶纵梁厚度、B 柱内部材料、地板内侧材料、障碍高度、障碍撞击位置，约束条件分别是腹部负荷、上部粘性标准、中部粘性标准、下部粘性标准、上部肋骨偏转、中部肋骨偏转、下部肋骨偏转、耻骨联合力、B 柱中间点速度和B柱前门速度。

其数学模型如下：目标函数：

约束条件：

变量范围：

IDMO 算法与对比算法求解汽车碰撞优化问题的实验结果如表5所示。从表5中可直观看出，IDMO算法得到的最小质量为23.256 9，该结果不仅优于原始DMO算法，且小于其余的对比优化算法，说明IDMO 算法在求解该类工程问题时具有良好的工程实用性。

表5 汽车碰撞优化问题实验结果Table 5 Experimental results of car crashworthiness optimization

5 总结

本文为提高DMO 算法的收敛速度和寻优性能，提出了一种融合透镜成像反向学习的精英池侏儒猫鼬优化算法（IDMO）。使用13 个标准测试函数及Wilcoxon秩和检验对IDMO 算法进行仿真实验，实验结果表明，IDMO算法具有良好的寻优性能和鲁棒性，再通过将其应用于汽车碰撞优化问题实例，验证了IDMO算法在工程方面的适用性和可行性。在后续的研究中，考虑将算法应用在其他工程问题求解中，更深入地验证改进算法的性能。